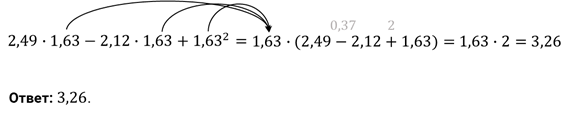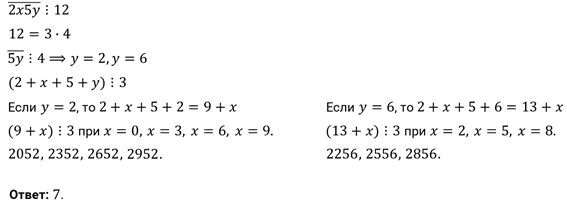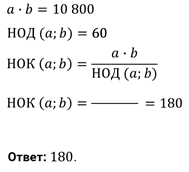Что такое общее свойство чисел в математике 5 класс

Презентация по математике на тему свойства чисел (5 класс)

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Фокусы с числами Подготовила учитель математики МКОУ СОШ №2 им.Н.Д.Рязанцева г.Семилуки Воронежской области Манаенкова Наталья Алексеевна

Тайны фокусов Все фокусы с числами основаны на законах умножения и признаках деления чисел

ФОКУС 1 Угадай число Задумайте число. Это число умножьте на 2. Прибавьте к результату 8. Разделите результат на 2. Отнимите задуманное число. У Вас получилось число 4! Книга математических фокусов

ФОКУС 2 Как найти задуманное четное число? Задумайте четное число Умножьте это число на 3 Полученное произведение разделите на 2 Частное опять умножьте на 3 Какие арифметические действия надо еще выполнить, чтобы получить задуманное число? Полученное частное разделить на 9 и умножить на 2 Книга математических фокусов

Пример-пояснение Задумали, например, четное число 12 12*3:2*3:9*2=12 Фокус основан на свойстве четных чисел: все четные числа делятся на 2. Понятно, что вместо 3 и 9 можно брать 5 и 25, т.е. любое число и его квадрат. Книга математических фокусов

ФОКУС 3 Угадай день рождения вы сможете угадать день рождения любого незнакомого человека,

Умножь на 2 число дня рождения. К произведению добавь 5 Сумму умножь на 50 К результату прибавь номер месяца рождения (июль — 7, январь — 1), Когда Вам назовут полученное число, вы называете день и месяц рождения. угадай мой день рождения Книга математических фокусов

Секрет фокуса «День рождения» Загадан день рождения. День — X, месяц — Y. Оба числа являются двузначными. Зритель выполняет следующие операции: Z – ответ от зрителя В уме отнимаем 250 Последние две цифры числа W — это месяц Y, остальные — день X. Пример. W=1305, значит Х=13, Y=05 День рожденья 13 мая

Фокус 4 “Угадать задуманное число”. Напишите на листе бумаги любое трехзначное число Припишите к нему это же число еще раз Получится шестизначное число Разделите это число на 7 Разделите полученное число на 11 Разделите полученное число на 13 Вы получили задуманное число! Книга математических фокусов

Разгадка фокуса 4 Когда мы к трехзначному числу приписали такое же число, то мы тем самым умножили его на 1001, а затем, разделив последовательно на 7, 11, 13, мы разделили его на 1001, то есть получили задуманное трехзначное число. Пример. 375 375375 375375:7=53625 53625:11=4875 4875:13= 375

Фокус 5 «КАЛЕНДАРЬ» Необходимо выбрать на календаре любой месяц и отметить в нем любой квадрат, содержащий 9 чисел. Если вы назовёте меньшее из чисел, я назову сумму всех девяти чисел. Например Книга математических фокусов Понедельник 1 8 15 Вторник 2 9 16 Среда 3 10 17

Секрет фокуса 5 А =1 Книга математических фокусов Здесь А=1. А А+7 А+14 S=9А+72 А+1 А+8 А+15 S=9(А+8) А+2 А+9 А+16

Проверка Возьмем календарь мая 2020 Наименьшее число 4. По горизонтали числа больше на 1 По вертикали числа больше на 7 По формуле имеем 9*4+72=108 Посчитаем без формулы 4+5+6+11+12+13+18+19+20=108 Книга математических фокусов

Сегодня мы рассмотрели самые простые фокусы с числами. Уловив закономерность Вы сами можете придумывать и загадывать фокусы с числами. Желаю Вам узнать новое о числах и с интересом провести время. Книга математических фокусов

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1168808

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

МГУ откроет первую в России магистерскую программу по биоэтике

Время чтения: 2 минуты

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

Костромская область разработала программу привлечения педагогических кадров

Время чтения: 2 минуты

Онлайн-конференция о профориентации и перспективах рынка труда

Время чтения: 3 минуты

Рособрнадзор объявил сроки и формат ЕГЭ

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Числа и их свойства

Урок 1. Подготовка к ЕГЭ по математике

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Числа и их свойства»

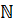
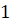
Напомним, что понятие «натуральное число» является первоначальным, неопределяемым. Оно возникло из потребностей счёта. Множество натуральных чисел обозначают . Наименьшее натуральное число — . Наибольшего натурального числа нет. Для записи натуральных чисел используют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Нуль не является натуральным числом.

Число, например, состоящее из а сотен, b десятков и c единиц, записывается в виде:

.

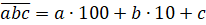
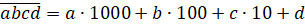
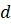
В следующей записи цифра а показывает количество тысяч, b — количество сотен, b — количество десятков и — количество единиц в числе.

Вы уже знаете, что натуральные числа можно сравнивать между собой, складывать и умножать. Из большего натурального числа можно вычесть меньшее.

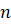
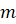
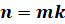
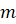
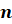
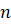
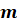
Если натуральное число делится на натуральное число без остатка, то есть , где , то число называют делителем числа , а число — кратным числа .

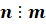
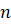
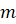
Вот такая запись означает, что делится на нацело.

Натуральное число, не равное единице, называется простым, если оно имеет только два делителя: единицу и само это число.

Например: 2, 3, 5, 7, 11, 17 — простые числа.

Натуральное число называется составным, если оно имеет более двух делителей. Например: 6, 15, 24, 36 — составные числа.

Число 1 не является ни простым, ни составным. Простых чисел бесконечно много. Каждое составное число разлагается на простые множители и притом единственным образом.

Сформулируем признаки делимости натуральных чисел:

1. Для делимости на 2 нужно, чтобы последняя цифра числа была чётная или .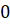

2. Для делимости на 3 нужно, чтобы сумма цифр числа делилась на 3.

3. Для делимости на 4 нужно, чтобы две последние цифры числа были 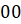или образовывали число, делящееся на 4.

4. Для делимости на 5 нужно, чтобы последняя цифра числа была 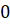или 5.

5. Для делимости на 8 нужно, чтобы три последние цифры числа были 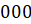или образовывали число, делящееся на 8.

6. Для делимости на 9 нужно, чтобы сумма цифр числа делилась на 9.

7. Для делимости на 10 нужно, чтобы последняя цифра числа была .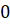

8. Для делимости на 11 нужно, чтобы разность между суммой цифр, стоящих на чётных местах, и суммой цифр, стоящих на нечётных местах, делилась на 11.

9. Для делимости на 25 нужно, чтобы две последние цифры числа были 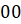или образовывали число (25, 50 или 75), делящееся на 25.

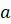
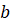
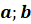
Наибольшее из натуральных чисел, на которое делятся числа и , называется их наибольшим общим делителем и обозначается НОД ().

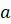
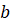
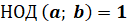
Числа и называются взаимно обратными, если .

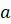
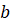
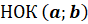
Наименьшее из натуральных чисел, которое делится на числа и , называется их наименьшим общим кратным и обозначается .

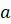
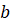
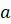
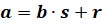
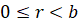
Разделить натуральное число на натуральное число с остатком – это значит представить в виде: , где .

Например, .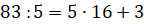

Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.

Задание первое. Найдите значение выражения .

Задание второе. Найдите наибольшее натуральное число, которое при делении на 15 с остатком даёт частное, равное 19.

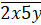
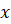
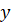
Задание третье. Найдите все натуральные числа вида (здесь — цифра сотен, — цифра единиц), которые делятся на 12. В ответ запишите их количество.

Задание четвёртое. Произведение двух чисел равно 10 800, а их НОД равен 60. Найдите НОК этих чисел.

Задание пятое. Найдите все пары натуральных чисел, НОД которых равен 5, а НОК равно 105.

Задание шестое. Сумма цифр искомого двузначного числа равна 8. Если цифры этого числа переставить, то получится число, которое меньше искомого на 18. Как велико искомое число?

Задание седьмое. В двузначном числе цифра десятков на 4 больше цифры единиц. Когда это число разделили на цифру единиц, то в частном получилось 24, а в остатке число, которое на 2 меньше делителя. Найдите заданное число.

Задание восьмое. В комнате стоят табуретки и стулья. У каждой табуретки по 3 ноги, у каждого стула по 4 ноги. Когда на всех табуретках и стульях сидят люди, то в комнате всего 39 ног. Сколько стульев и сколько табуреток в комнате?

Задание девятое. Когда брату было столько лет, сколько сестре сейчас, им вместе было 15 лет; когда сестре будет столько лет, сколько сейчас брату, им вместе будет 27 лет. Найдите возрасты брата и сестры.

Источник

«Любопытные свойства чисел». 5-й класс

Разделы: Математика

Класс: 5

«Мы… никогда не стали бы разумными, если бы исключили число из человеческой природы» (Платон)

Название «арифметика» происходит от древнегреческого слова arithmos – число. В понятии числа важны два момента. Во-первых, каждое число, например 5, выражает то общее, что присуще каждому множеству из 5 предметов. Во-вторых, каждое число есть результат пересчёта, начинающегося с единицы и завершающегося данным числом. Первые представления о числах формируются в глубинах мифологического сознания. В мифе число неразрывно связано с его символическим значением.

Арифметика мифа принадлежала к особому типу математической культуры. Она отличалась от современной математики тем, что её интересовал не весь ряд чисел, а только особо значимые из арифметических операций: сложение и умножение.
Некоторые народы использовали словесную систему нумерации. Например, у древних индусов она была следующей:

Слова, используемые для выражения чисел

0Пустой, небо, отверстие

1Начало, луна, земля, брахман

2Близнецы, ноздри, глаза, губыПодумайте, какими словами можно было бы обозначить другие числа?
Учащиеся предлагают различные варианты, которые записываются на доске.
Затем открывается данная таблица, и анализируются предложенные варианты с исторической и математической точек зрения.3Время, миры, огонь4Океаны, касты, страны света5Стрелы, легендарные герои «Махабхараты»6Части тела, цвета7Горы, мудрецы, отшельники8Змеи, слоны9Богини10Пальцы, воплощения бога «Вишну»12Боги14День, половина месяца20Ногти33Зубы

Почему числа записаны в таком порядке? (индусы записывали справа налево)
Попробуйте записать на языке индусов числа: 452; 38; 781.
Занимательное умножение. Парад чисел.
Арифметические действия с числами обладают рядом интересных закономерностей. Давайте посмотрим некоторые из них.

Свойство числа 481. Казалось бы, что может быть интересного у такого числа? Но тем не менее:

Его объяснениеВозьмём какое-либо двузначное число, например 12. Удвоим его и припишем справа 0. К результату (240) прибавим исходное число. Получится 252. Умножим это число на 481 и получим: 252*481=121212.
Возьмём другое двузначное число, например 23, и проделаем с ним те же операции. 23*2=46, 460+23=483, 483*481=232323.
В обоих случаях в результате получилось шестизначное число, в записи которого трижды повторяется исходное число. Как можно объяснить этот удивительный факт?Если взять двузначное число a, удвоить его и приписать справа 0, то получится число 20а. Добавив к нему исходное число а, получим 21а. Секрет загадочного умножения скрыт в равенстве 21*481=10101. Имеем 21а*481 =а*10101. То, как легко видеть, есть число, в записи которого участвует три раза двузначное число а.

Угадывание чисел.
Иногда занятия математикой превращаются в увлекательные приключения с числами. Вот два таких примера.

Пример: Задуманы числа 3 и 4. Перемножая их, получим 12, вычитаем из этого числа наименьшее из загаданных чисел. Имеем 9, после умножения чисел 9 и 3 получим число 27. Последняя цифра результата 7, по таблице находим, что были загаданы числа 3 и 4.
Обоснование. Пусть задуманы числа k и k+1, где 0

Подведение итогов занятия. Предложить учащимся найти другие интересные закономерности чисел к следующему занятию.
Во время данного занятия у учащимися созданы условия для формирования следующих УУД:

Источник