Что такое однокартинный чертеж
Обратимость чертежа



Вышеприведенные чертежи называются однокартинными. Однокартинный чертеж не обладает свойством обратимости. Проекционный чертеж становится обратимым при добавлении дополнительной информации.
горизонтальная проекция точки А; А2 – фронтальная проекция точки А; А1А2— линия связи. Если на К.Ч. заданы две проекции точки, точка однозначно задана на К.Ч.
На рис. 7 приведен комплексный чертеж прямой АВ. Прямая однозначно задана на комплексном чертеже, если заданы две ее проекции.


| Рис. 8 |
| Рис.10 |
| Рис.9 |
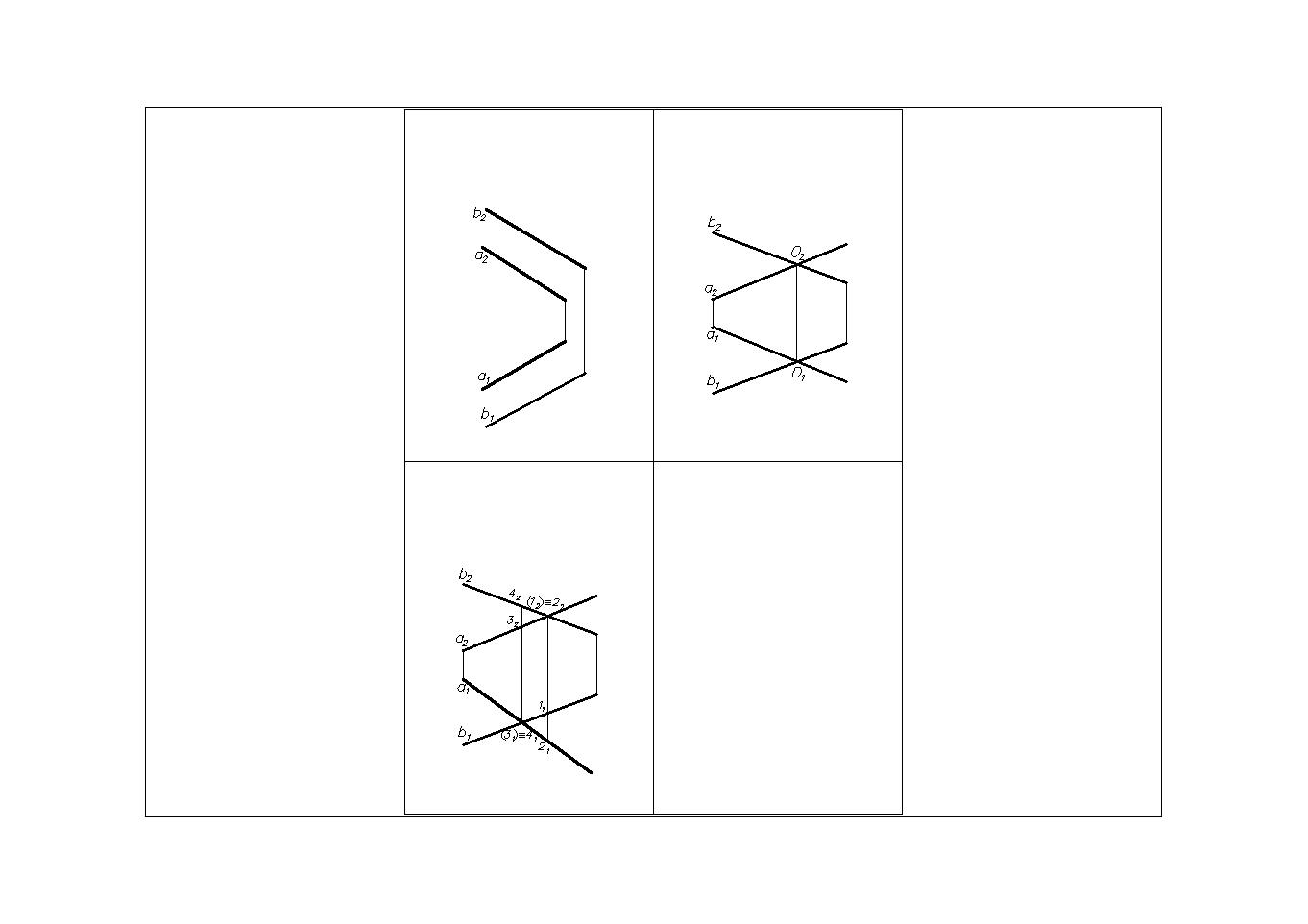
1. Параллельные прямые. Две прямые параллельны между собой, если их одноименные проекции тоже параллельны (Рис.8). Если aIIb, то a1IIb1и a2IIb2.
2. Пересекающиеся прямые (имеют одну общую точку). Две прямые пересекаются между собой, если точки пересечения одноименных проекций прямых лежат на одной линии связи (Рис.9). Если a xb = О,тоa1xb1 = О1 иa2xb2. = О2.
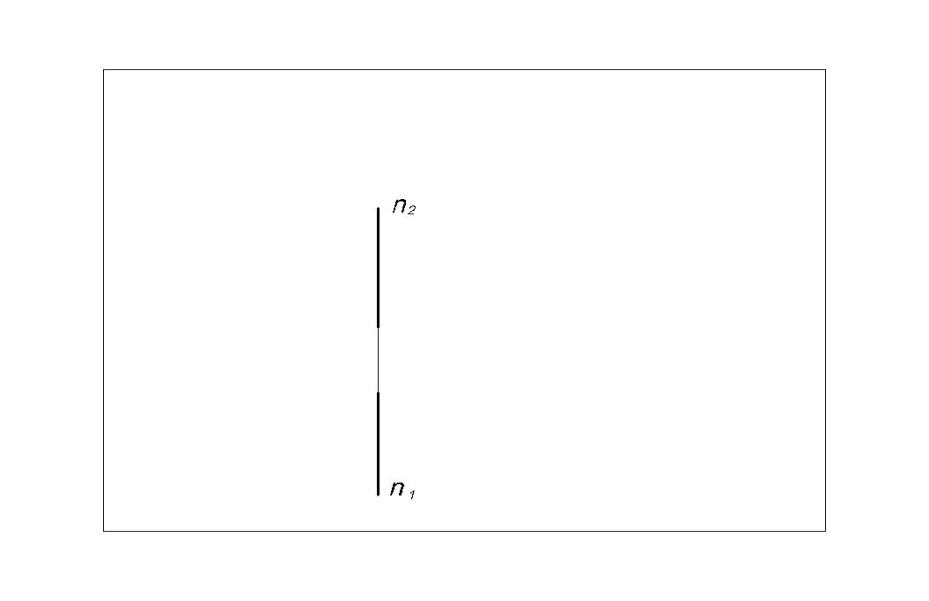
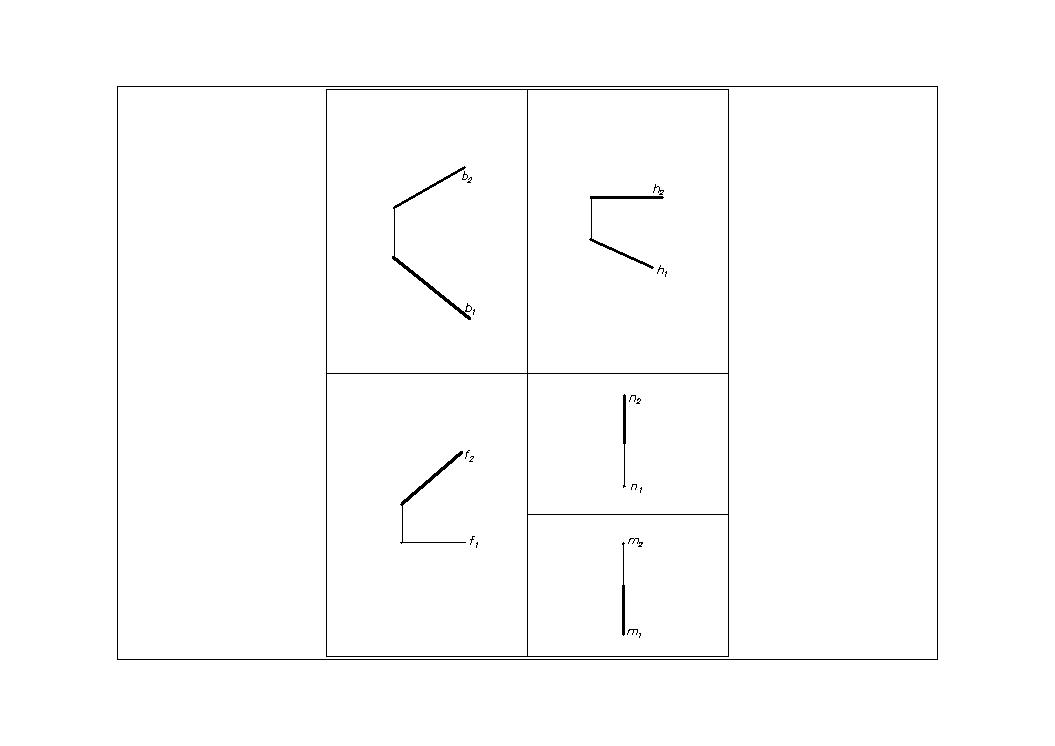
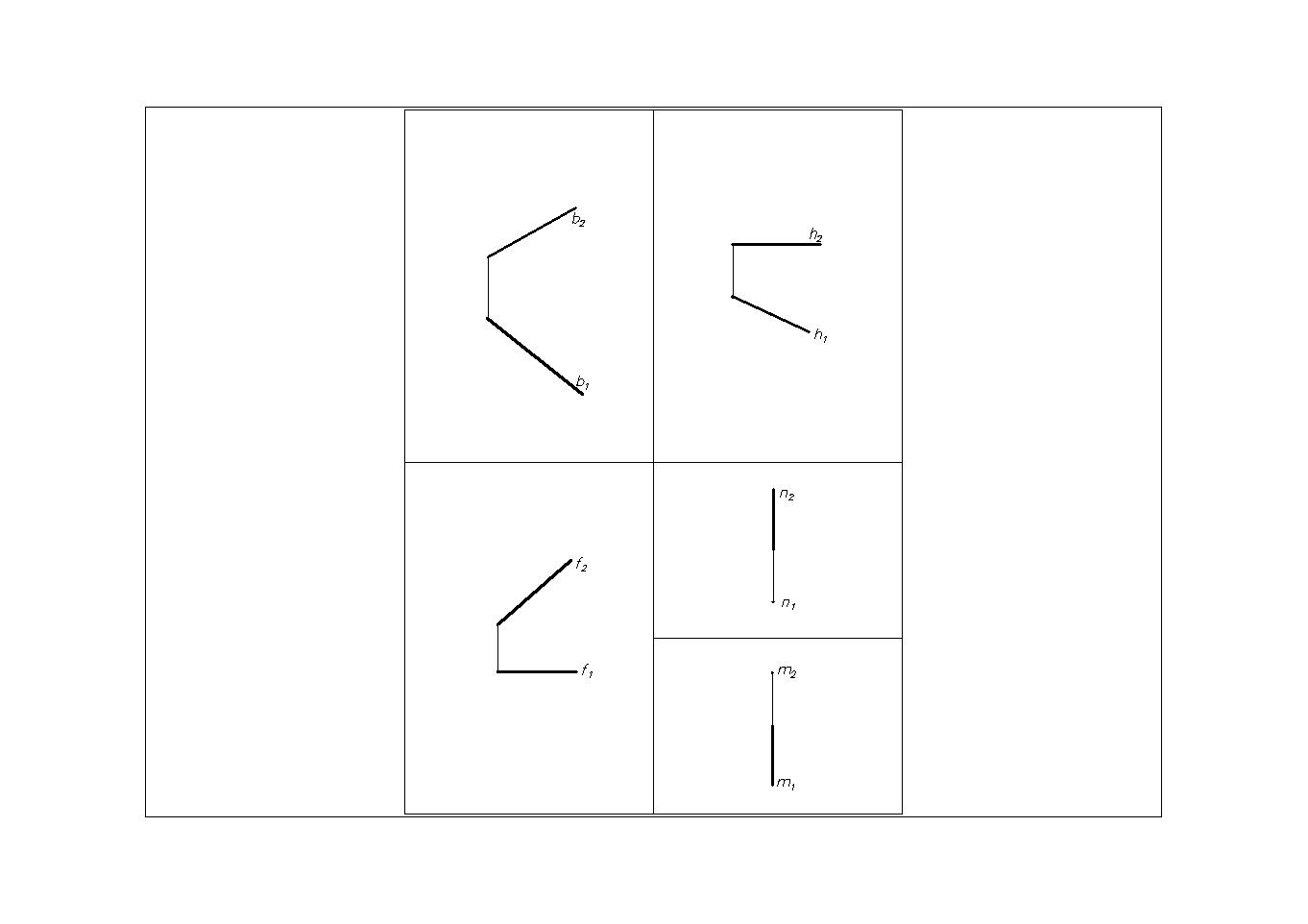

Рис.11 Рис.12 Рис.13 Рис.14
В зависимости от своего положения относительно плоскостей проекций прямые разделяют на прямые общего положения и прямые частного положения.
Прямая общего положения (Рис.11) – прямая, которая имеет углы, отличные от 0 и 90 одновременно со всеми плоскостями проекции (П1, П2).
Прямые, которые параллельны плоскостям проекций или перпендикулярные к ним называются прямыми частного положения.
Фронталь (Рис.13) – линия, все точки которой имеют одинаковую координату Y (ордината). Фронталь параллельна фронтальной плоскости проекций. Обозначение фронтали – f(fIIП2). На П2 f2= f, f2— натуральная величина отрезка АВ.
Профильная линия(Рис.14)– линия, все точки которой имеют одинаковую координату X (абсцисса). Профильная линияпараллельна профильной плоскости проекций. Обозначим профильную линию буквой п (пII П3). На П1 и П2 проекции профильной линии п совпадают с линией связи.
Комплексный чертеж точки



Теорема о проецировании прямого угла.
Если один из катетов прямого угла параллелен плоскости проекций, а второй не занимает проецирующего положения (не перпендикулярен плоскости проекций), то данный прямой угол на эту плоскость проекций проецируется без искажения.
Вышеприведенные чертежи называются однокартинными. Рассмотренные методы проецирования позволяют однозначно решить прямую задачу – построить проекцию (чертеж) геометрического образа.
Обратная задача начертательной геометрии – по данному чертежу реконструировать геометрический образ – решается неоднозначно (может быть несколько или бесчисленное множество решений). Из этого следует, что однокартинный чертеж не обладает свойством обратимости. Проекционный чертеж становится обратимым при добавлении дополнительной информации.
В нашем курсе мы будем применять обратимый чертеж, который называется комплексным чертежомв ортогональных проекциях (К.Ч.)
Комплексным чертежом называется чертеж, составленный из двух или более связанных между собой ортогональных проекций изображаемого геометрического образа.
Принцип образования: геометрический образ ортогонально проецируется минимум на две взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещаются с одной плоскостью.
 |
Условные обозначения точек – A,В,С,D… 1,2,3… и т.д.;
П1(XOY) – горизонтальная плоскость
П2(XOZ) – вертикальная (фронтальная) плоскость проекции;
А1 – горизонтальная проекция точки А на плоскость П1;
А2 – фронтальная проекция точки А на плоскость П2.
Рис.6 Чертеж на рис.6 является однокартинным.
Чертеж на рис. 7 называется комплексным чертежем точки А.
А1 – горизонтальная проекция точки А;
А1А2- линия связи.
Оба чертежа (рис.6 и рис.7) являются графической иллюстрацией ортогонального проецирования одной и той же точки А на две взаимно перпендикулярные плоскости (П1 и П2).
Если на К.Ч. заданы две проекции точки, можно утверждать, что точка однозначно задана на К.Ч.
Ортогональное проецирование. Свойства ортогонального проецирования
Ортогональное (прямоугольное) проецирование является частным случаем параллельного проецирования, когда направление проецирования перпендикулярно к плоскости проекций (s^П1). В этом случае проекции геометрических фигур называются ортогональными.
Ортогональному проецированию присущи все свойства параллельного проецирования, а также свойства, присущие только ортогональному проецированию.
Первое свойство. В общем случае ортогональная проекция отрезка всегда меньше его натуральной длины.
Рассмотрим частные случаи:
Если a = 0 Þ |А1В1 | = |АВ |, т.е. проекция равна самому отрезку.
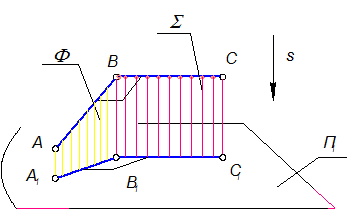
Второе свойство: теорема о проецировании прямого угла
Если одна сторона прямого угла параллельна какой-нибудь плоскости проекций, а вторая сторона не перпендикулярна ей, то на эту плоскость проекций прямой угол проецируется без искажения.
плоскость Ф = АВ Ç ВВ1
плоскость S = ВС Ç ВВ1
Третье свойство: ортогональная проекция окружности в общем случае есть эллипс.
Для получения обратимых однокартинных чертежей их дополняют необходимыми данными. Существуют различные способы такого дополнения. Например, чертежи с числовыми отметками.
Способ заключается в том, что наряду с проекцией точки А1 задаётся высота точки, т.е. её расстояние от плоскости проекций. Задают, также, масштаб. Такой способ используется в строительстве, архитектуре, геодезии и т. д. Однако, он не является универсальным для создания чертежей сложных пространственных форм.
В 1798 году французский геометр-инженер Гаспар Монж обобщил накопленные к этому времени теоретические знания и опыт и впервые дал научное обоснование общего метода построения изображений, предложив рассматривать плоский чертёж, состоящий из двух проекций, как результат совмещения двух взаимно перпендикулярных плоскостей проекций. Отсюда ведёт начало принцип построения чертежей, которым мы пользуемся и поныне.
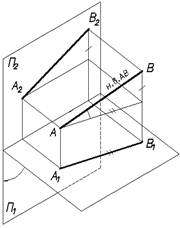
Поставим перед собой задачу построить проекции отрезка [AB] на две взаимно перпендикулярные плоскости проекций П1 и П2.
Пространственная модель.
П1 — горизонтальная плоскость проекций;
А1В1 — горизонтальная проекция отрезка;
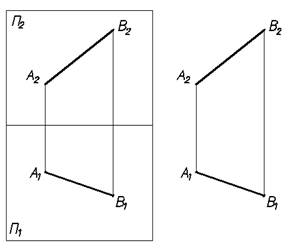
Плоская модель.
Свойства двухкартинного комплексного чертежа Монжа:
1. Две проекции точки всегда лежат на одной линии связи установленного направления.
2. Все линии связи одного установленного направления параллельны между собой.
Безосный чертёж.
Это обстоятельство имеет место в чертежах, применяющихся в технике, и такой чертёж называется безосным.
Проиллюстрируем вышесказанное на конкретном примере.
Задача: Составить чертёж для изготовления стола (рис. 1-18).
1.Построить три проекции стола, учитывая свойства эпюра Монжа.
2. Что не хватает для выполнения по чертежу данного изделия?
3. Да, конечно, размеров.
Теперь, когда есть три изображения изделия и его размеры, имеют ли значение для изготовления изделия расстояния от изделия до плоскостей проекций, т. е. привязка к осям x, y и z (размеры 1500, 2000, 2000 на чертеже).
Безосный чертеж позволяет, не привязываясь к осям, располагать изображения в удобном для исполнителя положении, но с соблюдением проекционной связи, т.е. построение чертежа происходит по законам, установленным Гаспаром Монжем
Однокартинный чертеж необратим, поэтому фигуру (оригинал) проецируют на 2 или 3 взаимно перпендикулярные плоскости проекций. В техническом черчении применяется до шести основных плоскостей проекций.
Спроецируем т. Ана 2 пл. проекций (рис.1.6):

 |
p2 — фронтальная;
Из точкиА опустим перпендикуляры на пл. p1 и пл. p2, получим соответственно:
А¢— горизонтальная проекция т. А; А¢¢-фронтальная проекция точки А.
Совмещая 3 пл. пр. в единую плоскость чертежа, получим комплексный чертёж (рис.1.7.).
1.6. Свойства комплексного чертежа.
1. Две проекции точки вполне определяют её положение в пространстве.
2. Две проекции точки всегда лежат на одной линии связи, пер- пендикулярной оси проекций. (A¢A¢¢)^ X и (A¢¢A¢¢¢)^ Z
Л Е К Ц И Я 2. Комплексный чертёж прямой линии.
2.1. Задание и изображение прямой. Принадлежность точки прямой.

Используя 3 – е свойство параллельного проецирования, можно сделать вывод о принадлежности точки прямой линии:
Способы дополнения однокартинного чертежа
Центральное проецирование
Суть метода заключается в том, что предметы (точки, прямые, плоскости, поверхности), находящиеся в пространстве, проецируются на некоторую плоскость лучами, выходящими из одной точки.
Изображение предметов при помощи центрального проецирования обладает хорошей наглядностью, но по такому изображению трудно определить истинную форму и размеры предмета. Проецирование широко применяется в изобразительном искусстве (при построении перспективы), в кинематографии.
При составлении машиностроительных чертежей пользуются другим методом проецирования – параллельным.
Параллельное проецирование

Параллельное проецирование отрезка АВ на плоскость П’ представлено на рис. 1.1. Лучи, выходящие из точек А и В, параллельны между собой и параллельны заданному лучу 
Свойства параллельного проецирования
Параллельное проецирование обладает большими возможностями решения графических задач на основе таких свойств: проекцией точки является точка, прямой – прямая линия, параллельных прямых – параллельные прямые. Если точка делит отрезок прямой в некотором отношении, то и проекции отрезка находятся в таком же отношении.
В зависимости от направления проецирующего луча по отношению к плоскости П’ параллельное проецирование может быть косоугольным (φ ≠ 90°) или прямоугольным (φ = 90°) – ортогональным.
Все машиностроительные чертежи выполняются на основе ортогонального проецирования, так как в этом случае легко устанавливается соотношение между длиной отрезка и его проекциями и соблюдается свойство о проецировании прямого угла плоскости. Читается это свойство так: прямой угол проецируется на плоскость в общем случае с искажением, но одна из сторон пря-
мого угла параллельна плоскости проекций – в этом случае проекция прямого угла – 90°. Это свойство является важным при решении геометрических задач.
Рассмотренные методы проецирования предмета на одну плоскость проекций позволяют однозначно решать прямую задачу, т. е. по данному оригиналу строить его чертежи. Однако обратная задача – по данному чертежу воспроизвести оригинал – не решается однозначно. В этом случае говорят – “чертеж необратим”. Для получения обратимых чертежей существуют различные методы дополнения однокартинного чертежа.
Способы дополнения однокартинного чертежа
Способ с числовыми отметками.Суть способазаключается в том, что недостающая в плоскости проекций пространственная координата отмечается на чертеже числом. Этот способ широко применяется в топографии, при пост-роении профиля дорог, в том числе железнодорожного пути.
Способ академика Федорова. Принципиальное отличие от предыдущего способа состоит в том, что числовые отметки заменяются масштабными отрезками. Способ в основном применяется в кристаллографии.
Способ составления аксонометрических проекции применяют в строительных и машиностроительных чертежах в основном для наглядного изображения предмета.
Способ составления комплексного чертежа наиболее широко применяется при составлении строительных и машиностроительных чер-
тежей.
2. ТОЧКА, ПРЯМАЯ И ПЛОСКОСТЬ НА КОМПЛЕКСНОМ
ЧЕРТЕЖЕ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Прежде чем перейти к изображению геометрических элементов на комп-лексном чертеже, рассмотрим положение некоторой точки А в пространственной системе координат – X, Y, Z (рис. 2.1).


А3 – профильная. Координаты Аx, Ay, Az определяют положение этой точки в пространстве. Такое наглядное изображение точки, находящейся в пространстве, дает представление о расположении точки относительно плоскостей проекций П1, П2, П3. Однако в этом случае искажаются действительные размеры в системе координат и, самое главное, затрудняется чтение чертежа при изображении сложных предметов. Французский геометр Г. Монж предложил перейти от такого изображения предмета к комплексному чертежу. Комплексный чертеж – это ортогональное изображение предмета на две или более взаимоперпендикулярные плоскости проекций, совмещенные с плоскостью чертежа. Это совмещение происходит следующим образом: плоскости П1 и П3 поворачиваются относительно осей X и Z до положения,
когда они составляют одну плоскость с П2 (рис. 2.2).
На таком комплексном чертеже точка будет изображаться своими проекциями. Чтобы точка на чертеже была задана, достаточно иметь две ее проекции. Размеры представляются на комплексном чертеже в натуральную величину. Предмет можно изучать спереди, сверху, слева, но при этом необходимо иметь навыки пространственного представления на таком чертеже.
Прямая на комплексном чертеже может быть задана двумя точками или своими проекциями. Минимальное количество проекций прямой на чертеже – две (рис. 2.3).

3. ПРЯМЫЕ И ПЛОСКОСТИ ОБЩЕГО И ЧАСТНОГО ПОЛОЖЕНИЯ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Прямые общего положения
Прямые общего положения наклонены ко всем плоскостям проекций и пересекают их. Точки пересечения прямой с плоскостями проекций называются следами прямой. Иногда бывает необходимо их определять. Пусть на чертеже дана прямая а, определим ее следы (рис. 3.1).
Чтобы определить точку пересечения прямой с горизонтальной плоскостью проекций – горизонтальный след, надо продолжить фронтальную проекцию прямой аα до пересечения с осью X, провести перпендикуляр к оси X, продолжить горизонтальную проекцию прямой а1 до пересечения с перпендикуляром. Горизонтальный след обозначается буквой Н. Необходимо обратить внимание на то, что сама точка Н присутствует на чертеже, так как Z = 0, т. е. точка принадлежит плоскости П1.