Что такое однородная величина

Понятие величины, свойства однородных величин

Этапы исторического развития способов измерения величин. Происхождение названий единиц измерения величин

1. Сравнение величин путем приложения предметов друг к другу.

2. Сравнение величин с помощью предмета-посредника (условной мерки).

3. Сравнение и измерение величин с помощью частей тела (локоть, ладонь).

4. Сравнение и измерение величин с помощью универсальных общепринятых условных мерок:

— чарка, штоф, бочка (для объемов),

— локоть, сажень, аршин (для расстояний),

— пуд, лот, фунт (для масс).

5. Введение метрической системы. Предложена в конце 18 в. учеными в Париже. Эта система мер принята не во всех странах. В СССР она использовалась с 1917 года. За основу измерения был принят метр (в пер. с греческого «измеряю»), величина которого равна приблизительно

1/40 000 000 части Гринвичского меридиана. Все остальные единицы измерения величин связаны с метром. Так 1 кг равен массе 1 дм 3 дистиллированной воды, 1 л равен объему этой же воды. Все остальные единицы измерения в 10 n раз больше или меньше основных (мм, дм, км, г, мг, мл и т.п.).

Свойства однородных величин:

1) для двух величин одного рода справедливо только одно из вы­сказываний: х=у или х у;

2) Отношение «быть большим по величине» ( х>у) является отно­шением порядка. Например, отношение «быть тяжелее» на множестве всех яблок является антирефлексивным (любое из яблок не тяжелее самого себя), антисимметричным (если яблоко х тяжелее яблока у, то яблоко у не тяжелее яблока х), транзитивным (если яблоко х тяжелее яблока у и яблоко у тяжелее яблока z, то яблоко х тяжелее яблока z);

3) отношение «быть одинаковым по величине» (х=у) является от­ношением эквивалентности. Например, «быть одинаковым по массе» на множестве всех яблок рефлексивно (каждое яблоко одинаково по массе с самим собой), симметрично (если яблоко х одинаково по массе с яблоком у, то яблоко у одинаково по массе с яблоком х), транзитивно (если яблоко х одинаково по массе с яблоком у и яблоко у одинаково по массе с яблоком z, то яблоко х одинаково по массе с яблоком z);

4) однородные величины можно складывать. Сложение величин обладает следующими свойствами:

а) переместительности, т.е. х+у=у+х,

б) сочетательности, т.е. x+(y+z)=(x+y)+z,

в) монотонности, т.е. х

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Основные положения однородных величин

Натуральное число как мера величины

Нам известно, что числа возникли из потребности счета и измерения. Если для счета предметов нам достаточно натуральных чисел, то для измерения нам необходимы действительные числа. В начальной школе в качестве результата измерения выступают натуральные числа. Мы также встанем на эту позицию, определив натуральное число как меру величины. Выясним, какой смысл имеют арифметические действия над натуральными числами с этой позиции.

Натуральные числа будем рассматривать в связи с измерением положительных скалярных величин: длин, площадей, масс, времени и др.

§1. Понятие положительной скалярной величины.

Рассмотрим два высказывания:

1.Многие окружающие нас объекты имеют длину;

2. Стол имеет длину.

Таким образом, термин «длина» применим для обозначения свойства целого класса объектов или одного объекта. Длина, это такое свойство объекта или объектов, которое проявляется в разной степени, т.е. можно сказать, что один стол длиннее другого, чего нельзя сказать о форме стола или о материале, из которого он сделан. Мы не можем сказать, что один стол «прямоугольнее» другого или «деревяннее»другого.

Таким образом, свойство «длина»- это особое свойство объектов, которое проявляется при сравнении их по протяженности. В процессе сравнения устанавливается, что два объекта либо имеют равные длины, либо длина одного больше длины другого объекта. Такие свойства объектов будем называть величинами.

Величины, выражающие одни и те же свойства объектов будем называть величинами одного рода или однородными величинами.

Основные положения однородных величин

1. Любые величины одного рода сравнимы: А=В либо А В.

2. Отношение «меньше» для однородных величин транзитивно: А А В.

5. Величину можно умножать на положительное действительное число, в результате получают величину того же рода х·А=В.

6. Величины одного рода можно делить, в результате получают число. Определение: Частным величин А и В называется такое положительное число х=А:В, что А=х∙В (деление определено через умножение величины на число).

Величины обладают одной особенностью, их можно оценить количественно. С этой целью величину надо измерить. Для измерения величины данного рода выбирают величину, называемую единицей измерения. Её будем обозначать Е.Если задана величина А и выбрана единица величины Е (того же рода), то измерить величину А – это значит найти такое положительное число х, что А=х·Е, х- численное значение величины А при выбранное единице величины Е или мера величины А при единице Е. Пишут х=m_Е(А).

Пример 1. А-длина отрезка а, Е- длина отрезка b, который в отрезке a укладывается 4 раза, тогда 4- мера длины отрезка а.

Пример 2. 2,6 кг=2,6∙кг, 13см=13·см, 16 с =16∙с.

Используя это представление, можно обосновать переход от одной единицы величины к другой.

ч= ·ч= ∙(60мин)= ( ∙60)мин=25мин.

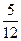
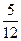
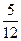
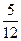
Определение.Величина, определяемая только численным значением, называется скалярной.

Определение.Величина, которая при выбранной единице измеренияопределяется положительным числом, называется положительной скалярной величиной.

Измерение величин позволяет переходить от сравнения величин к сравнению чисел, от действий над величинами к действиям над числами и наоборот.

1. Если величины А и В измерены с помощью единицы величины Е, то

2. Если величины А и В измерены с помощью единицы величины Е, то

Пример. А=5кг, В=3кг. =>А+В=5кг+3кг=(5+3)кг=8кг.

3. Если величины А и В таковы, что В=х∙А, а величина измерена с помощью единицы величины Е, то В=х∙А m(B)=х∙ m(A)

Пример. Еслимасса В в 3 раза больше массы А и А=2кг, то В=3 ∙А=3∙(2кг) =(3∙2)кг=6кг.

Рассмотренные понятия: объект (предмет, явление, процесс), его величина, её мера, единица величины- надо уметь вычленять в текстах и задачах.

Один и тот же объект может обладать несколькими величинами: для человека – рост (длина), масса, возраст (время), процесс равномерного движения связывает три величины S=V·t.

Аксиоматическое определение величины см. стр. 275.

Источник

Понятие величины

Величина – одно из основных математических понятий, воз­никшее в древности и в процессе длительного развития подверг­шееся ряду обобщений. Длина, площадь, объем, масса, скорость и многие другие – все это величины.

Величина — это особое свойство реальных объектов или явле­ний. Например, свойство предметов «иметь протяженность» назы­вается «длиной». Величину рассматривают как обобщение свойств некоторых объектов и как индивидуальную характеристику свой­ства конкретного объекта. Величины можно оценивать количест­венно на основе сравнения.

Например, понятие длины возникает:

1) при обозначении свойств класса объектов («многие окружающие нас предметы имеют длину»);

2) при обозначении свойства конкретного объекта из этого
класса («этот стол имеет длину»);

3) при сравнении объектов по этому свойству («длина стола
больше длины парты»).

Однородные величины – величины, которые выражают одно и то же свойство объектов некоторого класса.

Разнородные величины выражают различные свойства объ­ектов (один предмет может иметь массу, объем и др.).

Свойства однородных величин:

1. Однородные величины можно сравнивать.

Для любых величин а и b справедливо только одно из отно­шений: а b, а = b.

Например, масса книги больше массы карандаша, а длина ка­рандаша меньше длины комнаты.

2. Однородные величины можно складывать и вычитать. В
результате сложения и вычитания получается величина того же рода.

Величины, которые можно складывать, называются аддитив­ными. Например, можно складывать длины предметов. В резуль­тате получается длина. Существуют величины, которые не явля­ются аддитивными, например, температура. При соединении воды разной температуры из двух сосудов, получается смесь, темпера­туру которой нельзя определить сложением величин.

Мы будем рассматривать только аддитивные величины.

3. Величину можно умножать на действительное число. В
результате получается величина того же рода.

Пример: «Налей в банку 6 стаканов воды».

Если объем воды в стакане – V,то объем воды в банке – 6V.

4.Однородные величины делят. В результате получается не­отрицательное действительное число, его называют отношением величин.

Источник

Понятие измерения величины. Свойства скалярных величин.

Понятие измерения величины. Свойства скалярных величин.

Величина – неопределяемое понятие.

(Мы понимаем так: величина – это размер. Аристотель писал: «То или иное количество есть множество, если его можно счесть; есть величина, если его можно измерить».)

Под величиной понимают особые свойства реальных объектов или явлений.

-Какие величины вы знаете? (дл, масса, емкость…)

-Какие тройки взаимосвязанных величин? (ск, вр, рас)

-Каким методом пользуется учитель в нач. школе при ознакомлении с величинами (длиной)? (практическим)

Длина – это свойство предметов иметь протяжённость.

Масса – с математической точки зрения это такая положительная величина, которая обладает свойствами:

масса одинакова у тел, уравновешивающих друг друга на весах;

масса складывается, если тела соединяются вместе.

-Какие бывают величины?

(Разнородные величины- величины, которые выражают разные свойства объектов.

-Какие ещё бывают величины? (в геометрии векторная, скалярная; положительная, отрицательная; переменная, постоянная).

-Какие величины называются скалярными?

(Скалярные величины – величины, не имеющие направления или которые определяются одним численным значением.)

-Назовите свойства скалярных величин.

Свойства однородных скалярных величин

Любые две однородные величины сравнимы : они либо равны, либо одна меньше другой.

Т.е. для любых величин a и b справедливо одно и только одно из отношений:

Например, длина гипотенузы больше длины катета; масса яблока меньше массы арбуза, длины противоположных сторон прямоугольника равны.

Т.е. для любых величин a и b однозначно определяется величина

Например: пусть а- длина отрезка АВ, в – длина отрезка ВС. Тогда длина отрезка АС равна сумме длин отрезков АВ и ВС.

3. Величину можно умножать на неотрицательное действительное число, получая в результате число того же рода.

Например: если длину а отрезка АВ умножить на х=2, то получим длину 2а нового отрезка АС.

Например: Пусть а – длина отрезка АС, в – длина отрезка АВ, тогда длина ВС есть разность длин АС и АВ.

5. Величины одного рода делят, определяя частное через произведение величины на число:

Частным величин а и в называется такое неотрицательное действительное число х, что

Понятие измерения величины. Свойства скалярных величин.

Определение: Измерить величину значит сравнить её с некоторой величиной того же рода, принятой за единицу.

Определение: Если дана величина а и выбрана единица величины е, то в результате измерения величины а находят такое действительное число х, что а = x ● е.

Число x называют численным значением величины а при единице величины е.

Например, 8 кг = 8 1 кг.

Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой.

Выразить 1/5 часа в минутах.

1/5 ч = 1/5 ● 1 ч = 1/5 ● 60 мин = 60/5 мин = 12 мин.

Измерение величин позволяет свести сравнение их к сравнению чисел; операции над величинами к операциям над числами.

Не следует смешивать длину (она одна для отрезка) с численным значением длины, оно различно в зависимости от единицы измерения.

АВ = 4 см = 40 мм = 0,4 м

Свойства скалярных величин

Если величины а и в измерены при помощи единицы величины е, то отношения между величинами а и в будут такими же, как и отношения между их численными значениями и наоборот:

Пример: Сравните: 8 кг и 6 кг

Если величины а и в измерены при помощи единицы величины е, то чтобы найти численное значение суммы а + в , достаточно сложить численные значения величин а и в :

а +в = 3 m + 7 m = (3 + 7) m = 10 m

Например, а = 5 км, b в 3 раза больше длины а, то есть

b = 3 ● а = 3 ● (5 км) = (3● 5) км = 15 км

В начальном курсе математики, в частности в системе Л.В. Занкова, операции над величинами выполняются параллельно с операциями над их численными значениями. Например, в теме «Сложение отрезков» результат сложения можно найти 2 способами.

а =5см, в = 4 см. найти а+в.

Первый способ заключается в том, что строится отрезок = 5см и подстраивается 4 см. Получится всего 9 см.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Скоростное чтение

Курс повышения квалификации

Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-1047428

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

В Москве новогодние каникулы в школах могут начаться с 27 декабря

Время чтения: 1 минута

ЕГЭ в 2022 году пройдет в доковидном формате

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Величины и их измерения

Тема: ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЯ

Цель: Дать понятие величины, ее измерения. Познакомить с историей развития системы единиц величин. Обобщить знания о величинах, с которыми знакомятся дошкольники.

Понятие величины, их свойства. Понятие измерения величины. Из истории развития системы единиц величин. Международная система единиц. Величины, с которыми знакомятся дошкольники, и их характеристики.

1. Понятие величины, их свойства

Величина – одно из основных математических понятий, возникшее в древности и подвергшееся в процессе длительного развития ряду обобщений.

Первоначальное представление о величине связано с созданием чувственной основы, формированием представлений о размерах предметов: показать и назвать длину, ширину, высоту.

Под величиной понимаются особые свойства реальных объектов или явлений окружающего мира. Величина предмета – это его относительная характеристика, подчеркивающая протяженность отдельных частей и определяющая его место среди однородных.

Величины, характеризующиеся только числовым значением, называют скалярными (длина, масса, время, объем, площадь и др.). Кроме скалярных величин в математике рассматривают еще векторные величины, которые характеризуются не только числом, но и направлением (сила, ускорение, напряженность электрического поля и др.).

Скалярные величины могут быть однородными или разнородными. Однородные величины выражают одно и то же свойство объектов некоторого множества. Разнородные величины выражают различные свойства объектов (длина и площадь)

Свойства скалярных величин:

§ любые две величины одного рода сравнимы либо они равны, либо одна из них меньше (больше) другой: 4т5ц …4т 50кг Þ 4т5ц=4т500кг Þ 4т500кг>4т50кг, т. к. 500кг>50кг, значит

§ величины одного рода можно складывать, в результате получится величина того же рода:

2км921м+17км387м Þ 2км921м=2921м, 17км387м=17387м Þ 17387м+2921м=20308м; значит

§ величину можно умножать на действительное число, в результате получится величина того же рода:

12м24см × 9 Þ 12м24м=1224см, 1224см×9=110м16см, значит

§ величины одного рода можно вычитать, в результате получится величина того же рода:

4кг283г-2кг605г Þ 4кг283г=4283г, 2кг605г=2605г Þ 4283г-2605г=1678г, значит

§ величины одного рода можно делить, в результате получится действительное число:

8ч25мин :5 Þ 8ч25мин=8×60мин+25мин=480мин+25мин=505мин, 505мин :5=101мин, 101мин=1ч41мин, значит 8ч25мин :5=1ч41мин.

Величина является свойством предмета, воспринимаемым разными анализаторами: зрительным, тактильным и двигательным. При этом чаще всего величина воспринимается одновременно несколькими анализаторами: зрительно-двигательным, тактильно-двигательным и т. д.

Восприятие величины зависит от:

§ расстояния, с которого предмет воспринимается;

§ величины предмета, с которым он сравнивается;

§ расположения его в пространстве.

Основные свойства величины:

§ Сравнимость – определение величины возможно только на основе сравнения (непосредственно или сопоставляя с неким образом).

§ Относительность – характеристика величины относительна и зависит от выбранных для сравнения объектов один и тот же предмет может быть определен нами как больший или меньший в зависимости от того, с каким по размерам предметом он сравнивается. Например, зайчик меньше медведя, но больше мышки.

§ Изменчивость – изменчивость величин характеризуется тем, что их можно складывать, вычитать, умножать на число.

§ Измеряемость – измерение дает возможность характеризовать величину к сравнению чисел.

2. Понятие измерения величины

Потребность в измерении всякого рода величин, так же как потребность в счете предметов, возникла в практической деятельности человека на заре человеческой цивилизации. Так же как для определения численности множеств, люди сравнивали различные множества, различные однородные величины, определяя прежде всего, какая из сравниваемых величин больше, как меньше. Эти сравнения еще не были измерениями. В дальнейшем процедура сравнения величин была усовершенствована. Одна какая-нибудь величина принималась за эталон, а другие величины того же рода сравнивались с эталоном. Когда же люди овладели знаниями о числах и их свойствах, величине – эталону приписывалось число 1 и этот эталон стал называться единицей измерения. Цель измерения стала более определенной – оценить. Сколько единиц содержится в измеряемой величине. результат измерения стал выражаться числом.

Сущность измерения состоит в количественном дроблении измеряемых объектов и установлении величины данного объекта по отношению к принятой мере. Посредством операции измерения устанавливается численное отношение объекта между измеряемой величиной и заранее выбранной единицей измерения, масштабом или эталоном.

Измерение включает в себя две логические операции:

первая – это процесс разделения, который позволяет ребенку понять, что целое можно раздробить на части;

вторая – это операция замещения, состоящая в соединения отдельных частей (представленных числом мерок).

Деятельность измерения довольно сложна. Она требует определенных знаний, специфических умений, знания общепринятой системы мер, применения измерительных приборов.

В процессе формирования измерительной деятельности у дошкольников по средствам условной мерки дети должны понять, что:

§ измерение дает точную количественную характеристику величине;

§ для измерения необходимо выбирать адекватную мерку;

§ число мерок зависит от измеряемой величины (чем больше величина, тем больше ее численное значение и наоборот);

§ результат измерения зависит от выбранной мерки (чем больше мерка, тем меньше численное значение и наоборот);

§ для сравнения величин необходимо их измерять одинаковыми мерками.

3. Из истории развития системы единиц величин

Человек давно осознал необходимость измерять разные вели­чины, причем измерять как можно точнее. Основой точных измерений являются удобные, четко определенные единицы величин и точно воспроизводимые эталоны (образцы) этих единиц. В свою очередь, точность эталонов отражает уровень развития науки, техники и промышленности страны, говорит о ее научно-техническом потен­циале.

В истории развития единиц величин можно выделить несколько периодов.

Самым древним является период, когда единицы длины ото­ждествлялись с названием частей человеческого тела. Так, в ка­честве единиц длины применяли ладонь (ширина четырех пальцев без большого), локоть (длина локтя), фут (длина ступни), дюйм (длина сустава большого пальца) и др. В качестве единиц площади в этот период выступали: колодец (площадь, которую можно полить из одного колодца), соха или плуг (средняя площадь, обработанная за день сохой или плугом) и др.

В XIV—XVI вв. появляются в связи с развитием торговли так называемые объективные единицы измерения величин. В Англии, например, дюйм (длина трех приставленных друг к другу ячменных зерен), фут (ширина 64 ячменных зерен, положенных бок о бок).

В качестве единиц массы были введены гран (масса зерна) и карат (масса семени одного из видов бобов).

Следующий период в развитии единиц величин — введение еди­ниц, взаимосвязанных друг с другом. В России, например, такими были единицы длины миля, верста, сажень и аршин; 3 аршина составляли сажень, 500 саженей — версту, 7 верст — милю.

Однако связи между единицами величин были произвольными, свои меры длины, площади, массы использовали не только отдель­ные государства, но и отдельные области внутри одного и того же государства. Особый разнобой наблюдался во Франции, где каждый феодал имел право в пределах своих владений устанавливать свои меры. Такое разнообразие единиц величин тормозило развитие производства, мешало научному прогрессу и развитию торговых связей.

Новая система единиц, которая впоследствии явилась основой для международной системы, была создана во Франции в конце XVIII века, в эпоху Великой французской революции. В качестве основной единицы длины в этой системе принимался метр — одна сорокамиллионная часть длины земного меридиана, проходящего через Париж.

Кроме метра, были установлены еще такие единицы:

§ ар — пло­щадь квадрата, длина стороны которого равна 10 м;

§ литр — объем и вместимость жидкостей и сыпучих тел, равный объему куба с длиной ребра 0,1 м;

§ грамм — масса чистой воды, занимающая объем куба с длиной ребра 0,01 м.

Единица массы килограмм был определен как масса 1 дм3 воды при температуре 4 °С.

Так как все единицы величин оказались тесно связанными с единицей длины метром, то новая система величин получила назва­ние метрической системы мер.

В соответствии с принятыми определениями были изготовлены платиновые эталоны метра и килограмма:

§ метр представляла линей­ка с нанесенными на ее концах штрихами;

§ килограмм — цилинд­рическая гиря.

Эти эталоны передали на хранение Национальному архиву Франции, в связи с чем они получили названия «архивный метр» и «архивный килограмм».

Создание метрической системы мер было большим научным дос­тижением — впервые в истории появились меры, образующие стройную систему, основанные на образце, взятом из природы, и тесно связанные с десятичной системой счисления.

Но уже скоро в эту систему пришлось вносить изменения.

Оказалось, что длина меридиана была определена недостаточно точно. Более того, стало ясно, что по мере развития науки и техники значение этой величины будет уточняться. Поэтому от еди­ницы длины, взятой из природы, пришлось отказаться. Метром стали считать расстояние между штрихами, нанесенными на концах архивного метра, а килограммом — массу эталона архивного кило­грамма.

4. Международная система единиц

Международная система единиц (СИ) — это единая универсаль­ная практическая система единиц для всех отраслей науки, техники, народного хозяйства и преподавания. Так как потребность в такой системе единиц, являющейся единой для всего мира, была велика, то за короткое время она получила широкое международное призна­ние и распространение во всем мире.

В этой системе семь основных единиц (метр, килограмм, се­кунда, ампер, кельвин, моль и кандела) и две дополнительные единицы (радиан и стерадиан).

Как известно, единица длины метр и единица массы килограмм входили и в метрическую систему мер. Какие изменения претер­пели они, войдя в новую систему? Введено новое определение метра — он рассматривается как расстояние, которое проходит в вакууме плоская электромагнитная волна за долей секунды. Переход на это определение метра вызван ростом требований к точности измерений, а также стремлением иметь такую единицу величины, которая существует в природе и остается неизменной при любых условиях.

Определение единицы массы килограмма не изменилось, по-прежнему килограмм — это масса цилиндра из платиноиридиевого сплава, изготовленного в 1889 году. Хранится этот эталон в Меж­дународном бюро мер и весов в г. Севре (Франция).

Третьей основной единицей Международной системы является единица времени секунда. Она намного старше метра.

До 1960 года секунду определяли как часть солнечных суток, т. е. секунда определялась по вращению Земли вокруг своей оси. Это было сделано с таким расчетом, чтобы сохранить при­вычные отношения между различными единицами времени. При таком определении в сутках содержитсяс, что составляет 1440 мин, или 24 ч.

В 1960 году Генеральная конференция мер и весов приняла решение о переходе к единице времени, основанной на движении Земли по орбите вокруг Солнца. Секунду определили как часть года. Новое определение учитывало непостоянство средних солнечных суток и значительно повысило точность ее воспроизведения. Однако и это определение не удовлетворило ученых. В 1967 году секунду определили следующим образом: «Секунда равна периодам излучения, соответствую­щего переходу между двумя сверхтонкими уровнями основного состояния атома цезия- 133». В настоящее время имеется бо­лее точное определение секунды.

Вообще развитие науки и техники постоянно вносит свои кор­рективы в определения единиц величин.

Например, километр — это кратная единица, 1 км = 103×1 м = 1000 м;

миллиметр — это дольная единица, 1 мм=10-3 ×1м = 0,001 м.

Вообще, для длины кратной единицей являются километр (км), а дольными — сантиметр (см), миллиметр (мм), микрометр (мкм), нанометр (нм). Для массы кратной единицей является мегаграмм (Мг), а дольными — грамм (г), миллиграмм (мг), микрограмм (мкг). Для времени кратной единицей является килосекунда (кс), а дольными — миллисекунда (мс), микросекунда (мкс), наносекун­да (не).

5. Величины, с которыми знакомятся дошкольники, и их характеристики

Цель дошкольной подготовки — познакомить детей со свой­ствами объектов, научить дифференцировать их, выделяя те свойства, которые принято называть величинами, познако­мить с самой идеей измерения посредством промежуточных мер и с принципом измерения величин.

Длина — это характеристика линейных размеров предмета. В дошкольной методике формирования элементарных ма­тематических представлений принято рассматривать «длину» и «ширину» как два разных качества предмета. Однако в шко­ле оба линейных размера плоской фигуры чаще называют «длиной стороны», то же самое название используют при ра­боте с объемным телом, имеющим три измерения.

Длины любых предметов можно сравнивать:

§ приложением или наложением (совмещением).

При этом всегда мож­но либо приблизительно, либо точно определить, «на сколько одна длина больше (меньше) другой».

Масса — это физическое свойство предмета, измеряемое с помощью взвешивания. Следует различать массу и вес пред­мета. С понятием вес предмета дети знакомятся в 7 классе в курсе физики, поскольку вес — это произведение массы на ускорение свободного падения. Терминологическая некоррект­ность, которую позволяют себе взрослые в обиходе, часто пута­ет ребенка, поскольку мы иногда, не задумываясь, говорим: «Вес предмета 4 кг». Само слово «взвешивание» подталкивает к употреблению в речи слова «вес». Однако в физике эти ве­личины различаются: масса предмета всегда постоянна — это свойство самого предмета, а вес его меняется в случае измене­ния силы притяжения (ускорения свободного падения).

Для того чтобы ребенок не усваивал неправильную терми­нологию, которая будет путать его в дальнейшем в начальной школе, следует всегда говорить: масса предмета.

Кроме взвешивания, массу можно приблизительно опреде­лить прикидкой на руке («барическое чувство»). Масса — сложная с методической точки зрения категория для органи­зации занятий с дошкольниками: ее нельзя сравнить на глаз, приложением или измерить промежуточной меркой. Однако «барическое чувство» есть у любого человека, и на его исполь­зовании можно построить некоторое количество полезных для ребенка заданий, подводящих его к пониманию смысла поня­тия массы.

Основная единица массы – килограмм. Из этой основной единицы образуются другие единицы массы: грамм, тонна и пр.

Площадь — это количественная характеристика фигуры, указывающая на ее размеры на плоскости. Площадь принято определять у плоских замкнутых фигур. Для измерения пло­щади в качестве промежуточной мерки можно использовать любую плоскую форму, плотно укладывающуюся в данную фи­гуру (без зазоров). В начальной школе детей знакомят с палеткой — кусочком прозрачного пластика с нанесенной на него сеткой квадратов равной величины (обычно размером 1 см2). Накладывание палетки на плоскую фигуру дает возможность подсчитать примерное количество поместившихся в ней квад­ратов для определения ее площади.

В дошкольном возрасте дети сравнивают площади предметов, не называя этот термин, с помощью наложения предметов или визуально, путем сопоставления занимаемого ими места на сто­ле, земле. Площадь — удобная с методической точки зрения величина, поскольку позволяет организацию разнообразных про­дуктивных упражнений по сравнению и уравниванию площадей, определению площади путем укладывания промежуточных мер и через систему заданий на равносоставленность. Например:

1) сравнение площадей фигур методом наложения:

Площадь треугольника меньше площади круга, а площадь круга больше площади тре­угольника;

2) сравнение площадей фигур по количеству равных квад­ратов (или любых других мерок);

Площади всех фигур равны, так как фигуры состоят 4 равных квадратов.

При выполнении таких заданий дети в непрямой форме зна­комятся с некоторыми свойствами площади:

§ Площадь фигуры не изменяется при изменении ее поло­жения на плоскости.

§ Часть предмета всегда меньше целого.

§ Площадь целого равна сумме площадей составляющих его частей.

Эти задания также формируют у детей понятие о площади как о числе мер, содержащихся в геометрической фигуре.

Емкость — это характеристика мер жидкости. В школе ем­кость рассматривают эпизодически на одном уроке в 1 классе. Знакомят детей с мерой емкости — литром для того, чтобы в дальнейшем использовать наименование этой меры при ре­шении задач. Традиция такова, что с понятием объем в начальной школе емкость не связывают.

Время — это длительность протекания процессов. Понятие времени более сложное, чем понятие длины и массы. В обыденной жизни время — это то, что отделяет одно событие от другого. В математике и физике время рассматривают как скаляр­ную величину, потому что промежутки времени обладают свойствами, похожими на свойства длины, площади, массы:

§ Промежутки времени можно сравнивать. Например, на один и тот же путь пешеход затратит больше времени, чем велосипедист.

§ Промежутки времени можно складывать. Так, лекция в колледже длится столько же времени, сколько два урока в школе.

§ Промежутки времени можно вычитать, умножать на положительное действительное число.

§ Промежутки времени измеряют. Но процесс измерения времени отличается от измерения длины. Для измерения длины можно много­кратно использовать линейку, перемещая ее от точки к точке. Про­межуток времени, принятый за единицу, может быть использован лишь один раз. Поэтому единицей времени должен быть регулярно повторяющийся процесс. Такой единицей в Международной си­стеме единиц названа секунда. Наряду с секундой используются и другие единицы времени: минута, час, сутки, год, неделя, месяц, век.. Такие единицы, как год и сутки, были взяты из природы, а час, минута, секунда придуманы человеком.

Год — это время обращения Земли вокруг Солнца. Сутки — время обращения Земли вокруг своей оси. Год состоит приблизи­тельно из 365 — сут. Но год жизни людей складывается из целого числа суток. Поэтому вместо того, чтобы к каждому году прибав­лять 6 ч, прибавляют целые сутки к каждому четвертому году. Этот год состоит из 366 дней и называется високосным.

Календарь с таким чередованием лет ввел в 46 году до н. э. римский император Юлий Цезарь в целях упорядочивания сущест­вующего в то время очень запутанного календаря. Поэтому новый календарь называется юлианским. Согласно ему новый год начинает­ся с 1 января и состоит из 12 месяцев. Сохранилась в нем и такая мера времени, как неделя, придуманная еще вавилонскими астрономами.

Время смеет как физический, так и философский смысл. Поскольку ощущение времени субъективно, трудно полагаться на чувства в его оценках и сравнении, как это можно сделать в какой-то мере с другими величинами. В связи с этим в школе прак­тически сразу дети начинают знакомиться с приборами, изме­ряющими время объективно, т. е. независимо от ощущений человека.

При знакомстве с понятием «время» на первых порах на­много полезнее использовать песочные часы, чем часы со стрел­ками или электронные, поскольку ребенок видит, как сыплет­ся песок и может наблюдать «течение времени». Песочные часы удобно также использовать в качестве промежуточной меры при измерении времени (собственно, именно для этого они и придуманы).

Работа с величиной «время» осложнена тем, что время — это процесс, который не воспринимается сенсорикой ребенка непосредственно: в отличие от массы или длины, его нельзя потрогать или увидеть. Этот процесс воспринимается чело­веком опосредованно, по сравнению с длительностью других процессов. При этом привычные стереотипы сравнений: ход солнца по небу, движение стрелок в часах и т. п. — как прави­ло, чересчур длительны, чтобы ребенок этого возраста дейст­вительно мог их прослеживать.

В связи с этим «Время» — одна из самых трудных тем как в дошкольном обучении математике, так и в начальной школе.

Первые представления о времени формируются в дошколь­ном возрасте: смена времен года, смена дня и ночи, дети знако­мятся с последовательностью понятий: вчера, сегодня, завтра, послезавтра.

К началу школьного обучения у детей формируются пред­ставления о времени в результате практической деятельности, связанной с учетом длительности процессов: выполнение режимных моментов дня, ведение календаря погоды, знаком­ство с днями недели, их последовательностью, дети знакомят­ся с часами и ориентированием по ним в связи с посещением детского сада. Вполне возможно познакомить детей с такими единицами времени, как год, месяц, неделя, сутки, уточнить представление о часе и минуте и их длительности в сравнении с другими процессами. Инструментом измерения времени яв­ляются календарь и часы.

Скорость — это путь, пройденный телом за единицу вре­мени.

Скорость — величина физическая, ее наименования содер­жат две величины — единицы длины и единицы времени: 3 км/ч, 45 м/мин, 20 см/с, 8 м/с и т. п.

Очень трудно дать ребенку наглядное представление о ско­рости, поскольку это отношение пути ко времени, и ни изобра­зить его, ни увидеть невозможно. Поэтому при знакомстве со скоростью обычно обращаются к сравнению времени передви­жения объектов на равное расстояние или расстояний, прой­денных ими за одинаковое время.

Математически выполнить действие с именованными чис­лами можно следующим способом: выполнить действия с чис­ленными компонентами именованных чисел, а при записи от­вета добавить наименование. Такой способ требует соблюдения правила единого наименования в компонентах действия. Этот способ является универсальным. В начальной школе этим спо­собом пользуются и при выполнении действий с составными именованными числами. Например, для сложения 2 м 30 см + 4 м 5 см дети заменяют составные именованные числа на чис­ла одного наименования и выполняют действие: 230 см + 405 см = 635 см = 6 м 35 см либо складывают численные компоненты одних наименований: 2 м + 4 м = 6 м, 30 см + 5 см = 35 см, 6 м + 35 см = 6 м 35 см.

Эти способы используются при выполнении арифметичес­ких действий с числами любых наименований.

Источник