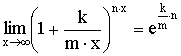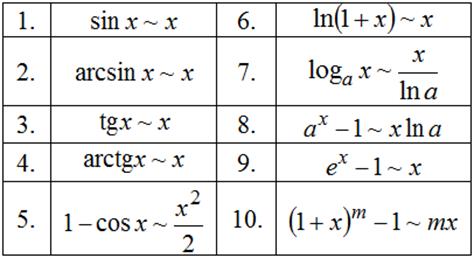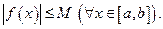Что такое ограниченность функции
Алгебра 9 класс. Урок№21-23. Возрастание и убывание функции.
Возрастание и убывание функции
Первое свойство, которое мы определим, это возрастание и убывание функции.
Функция называется возрастающей на множестве Х⊂D(f), если для любых х1 и х2, таких, что х1 f(x2). То есть большему значению аргумента, соответствует меньшее значение функции.
Понятия «возрастание» и «убывание» функции очень легко понять, если внимательно посмотреть на графики функции. Для возрастающей функции: мы как бы поднимаемся в горку, для убывающей соответственно — спускаемся. Общий вид возрастающих и убывающих функции представлен на графиках ниже.

Наибольшее и наименьшее значение
Наибольшее и наименьшее значение принято обозначать yнаиб. и yнаим..
Понятия ограниченности и наибольшего с наименьшим значением функции тесно связаны. Выполняются следующие утверждения:
а) Если существует наименьшее значение у функции, то она ограничена снизу.
б) Если существует наибольшее значение у функции, то она ограничена сверху.
в) Если функция не ограничена сверху, то наибольшего значения не существует.
г) Если функция не ограничена снизу, то наименьшего значения не существует.
Ребята мы с вами еще изучали понятия выпуклости функции. При решении некоторых задач, нам это свойство может понадобиться. Это свойство, также легко определяется с помощью графиков.
Функция выпукла вниз, если любые две точки графика исходной функции соединить, и график функции окажется ниже линии соединения точек.
Функция выпукла вверх, если любые две точки графика исходной функции соединить, и график функции окажется выше линии соединения точек.
Функция непрерывна, если график нашей функции не имеет разрывов, например, как график функции выше.
Если требуются найти свойства функции, то последовательность поиска свойств такова:
а) Область определения.
б) Монотонность.
в) Ограниченность.
г) Наибольшее и наименьшее значение.
д) Непрерывность.
е) Область значений.
Домашнее задание
Присылать ничего не нужно, проверка будет по выходу в школу!
Пусть 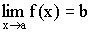

получаем 
Контрольный пример:

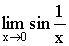
Бесконечно малые и их свойства.
Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если 


Основные свойства бесконечно малых функций (б.м.)
1° Сумма конечного числа б.м. функций является функцией бесконечно малой.
2° Произведение б функции на ограниченную есть функция бесконечно малая.
3° Произведение двух б.м функций есть функция бесконечно малая..
4° Произведение б.м функции на константу является бесконечно малой функцией.
5° Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция бесконечно малая.
6° Функция 
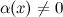
Основные теоремы о пределах.
Теорема 1. Предел суммы равен сумме пределов, если они
существуют:
Доказательство:

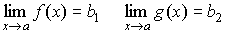
Из теоремы о связи между пределом и бесконечно малой величиной следует:


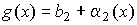
Получаем
Теорема 2. Предел произведения равен произведению пределов, если они существуют: 
Доказательство:


Из теоремы о связи между пределом и бесконечно малой величиной следует: 

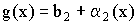
Получаем 
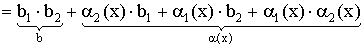


условии: все пределы существуют и 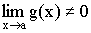
Доказательство:


Из теоремы о связи между пределом и бесконечно малой величиной следует:
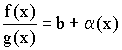

Получаем:
Теорема 4. Предел сохраняет знак неравенства. Если 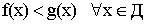

Доказательство:
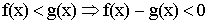
Следовательно, 

Следствие:
Теорема 5. Если функция ограниченна и монотонна на (a, b), то она имеет предел:
20-21. Первый и второй замечательные пределы и следствия.
Теорема. Первый замечательный предел 
Доказательство (геометрическое):
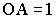
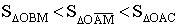

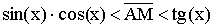
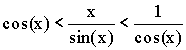

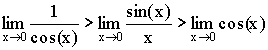
Так как 

Следствия из теоремы:
1) 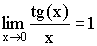
2) 
3) 
4) 
5) 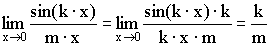
Теорема. Второй замечательный предел 
Доказательство:
Бином Ньютона:

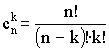
Используем бином Ньютона для доказательства неравенства: 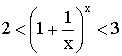

Отсюда заключаем, что 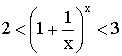
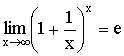
Следствия из теоремы:
1) 
2) 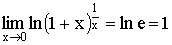
3) 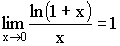
4)
22. Сравнения бесконечно малыхвеличин (б.м.в.) Эквивалентные бесконечно малые.
Непрерывность функции. Определение непрерывности функции в точке и на промежутке. Теорема об арифметических действиях над непрерывными функциями. Непрерывность сложной функции. Ограниченность непрерывной функции.
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Функция 

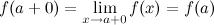
Функция 


Функция 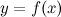
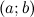
Функция 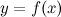

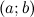




26. Теорема Вейерштрасса об ограниченности функции на замкнутом промежутке.
1) Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.
И 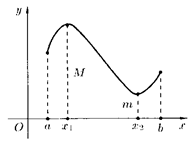
функция 
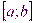
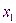



2) Если функция 

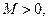
27. Теорема Больцано-Коши о промежуточном значении функции.
Если непрерывная функция, определённая на вещественном интервале, принимает два значения, то она принимает и любое значение между ними.
Следствия теоремы Больцано-Коши
1. Теорема о нуле непрерывной функции.
Если функция непрерывна на некотором отрезке и на концах этого отрезка принимает значения противоположных знаков, то существует точка, в которой значение функции равно нулю.
2. В частности любой многочлен нечётной степени имеет, по меньшей мере, один нуль.
§ 05. Свойства функций
Определение 1. Функция 
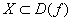
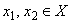
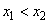
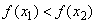
Определение 2. Функция 
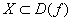
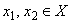
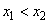
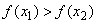
Монотонно возрастающие и монотонно убывающие функции называют монотонными.
Монотонные функции обладают следующими свойствами:
1) сумма двух монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;
2) произведение двух положительных монотонно возрастающих (монотонно убывающих) функций является монотонно возрастающей (монотонно убывающей) функцией;
3) если функция 
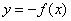
4) если положительная функция 
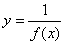
5) если функция 
Определение 3. Функция 
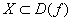
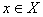

Определение 4. Функция 
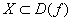
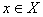
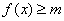
Ограниченная сверху и снизу на множестве Х функция называется ограниченной на этом множестве. Другими словами, если функция 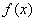
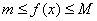
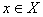
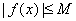
Определение 5. Точка 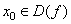

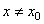
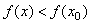
Определение 6. Точка 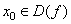

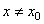
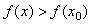
Точки максимума и минимума называют точками Экстремума функции.
Заметим, что функция в области своего определения может иметь несколько точек максимума или минимума.
Определение 7. Будем говорить, что в точке 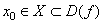

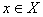
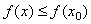
Определение 8. Будем говорить, что в точке 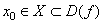

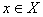
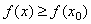
Если множество Х представляет собой отрезок [A; B], то наибольшее и наименьшее значения функция принимает либо в точке экстремума, либо на конце отрезка.
Говорят, что множество Х Симметрично относительно начала координат, если для любой точки 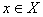
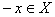
Определение 9. Функция 
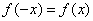
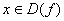
Определение 10. Функция 
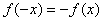
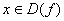
График четной функции имеет ось симметрии: так как точки 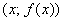
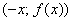
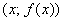
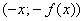
Четные и нечетные функции обладают следующими свойствами:
1) сумма двух четных (нечетных) функций есть функция четная (нечетная);
2) произведение двух четных (нечетных) функций есть функция четная; произведение четной и нечетной функций есть функция нечетная;
3) если нечетная функция 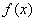
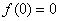
4) всякая функция, определенная на множестве Х, симметричном относительно начала координат может быть представлена в виде суммы двух функций, определенных на Х, причем одна из этих функций является четной, а другая – нечетной.
Определение 11. Функция 
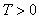
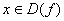
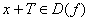
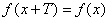
Наименьшее из чисел Т в определении 11 называют Периодом. Периодическая функция имеет бесконечно много периодов, все они кратны числу Т.
Все введенные в этом параграфе определения используются при исследовании функций и построении графиков.