Что такое оптимизационная задача

Понятие оптимизационных задач и оптимизационных моделей

Оптимизационными задачами в экономике называются экономико-математические задачи, цель которых состоит в нахождении наилучшего (оптимального) с точки зрения некото­рого критерия (критериев) варианта использования имею­щихся ресурсов (материальных, временных и пр.).

Общая структура оптимизационной модели состоит из целе­вой функции, принимающей значения в пределах ограничен­ной условиями задачи области (области допустимых решений), и из ограничений, характеризующих эти условия.

Целевая функция в самом общем виде определяется тремя моментами: управляемыми переменными; неуправляемыми переменными (зависящими, например, от внешней среды); видом (формой) зависимости между ними (видом функции).

Целевая функция связывает между собой различные вели­чины модели. Как правило, в качестве цели выбирается эконо­мический показатель (прибыль, рентабельность, себестоимость, валовая продукция и т. д.). Поэтому целевую функцию иногда называют экономической, критериальной.

(2.1)

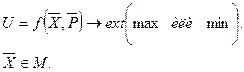
Система ограничений состоит из отдельных математичес­ких уравнений или неравенств, называемых балансовыми урав­нениями или неравенствами.

Ограничения подразделяются на:

а) линейные (I и II) и нелинейные (III и IV) (рисунок 2.1) (линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания; если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости являются нелинейными);

б) детерминированные (A, В) и стохастические (группы кри­вых С_i) (стохастические ограничения являются возможными, вероят­ностными, случайными) (рисунок 2.2).

Оптимизационные задачи вида (2.1) решаются методами математического про­граммирования. Существуют следующие основные методы математического программирования:

— методы линейного программирования требуют наличия системы взаимоувязанных факторов, критерия оценки оптимальности использования ресурсов, позволяют выбрать наилучшие способы использования имеющихся ресурсов;

— методы стохастического программирования, которыми решаются задачи планирования, если все или хотя бы часть параметров являются случайными величинами;

— методы динамического программирования, с помощью которых решаются линейные и нелинейные задачи, представленные в виде пошагового процесса;

— методы целочисленного программирования, с помощью которых решаются задачи с условием целочисленности переменных;

— методы выпуклого программирования;

— геометрическое программирование и др.

Выбор методов математического программирования для решения оптимизационных задач определяется видом целевой функции f, видом ограничений, определяющих область М, и специальными ограничениями на управляемые переменные (например, требованием их целочисленности, неотрицательности и т.д.).

Решением экономико-математической модели, или допу­стимым планом, называется набор значений неизвестных, ко­торый удовлетворяет ее системе ограничений. Модель имеет множество решений, или множество допустимых планов. Среди допустимых планов, удовлетворяющих целевой функции, как правило, имеется единственный план, называемый оптимальным, для которого целевая функция и критерий оптимальности имеют максимальное или минимальное значение. Если модель задачи имеет множество оптимальных планов, то для каждого из них значение целевой функции одинаково.

Если экономико-математическая модель задачи линейна, то оптимальный план достигается в крайней точке области изменения переменных величин системы ограничений. В случае нелинейной модели оптимальных планов и оптимальных значений целевой функции может быть несколько. Поэтому необходимо определять экстремальные планы и экстремаль­ные значения целевой функции. План, для которого целевая функция модели имеет экстремальное значение, называют экс­тремальным планом, или экстремальным решением.

Таким образом, для принятия оптимального решения лю­бой экономической задачи необходимо построить ее экономи­ко-математическую модель, по структуре включающую в себе систему ограничений, целевую функцию, критерий оптималь­ности и решение (оптимальный план).

Источник

Задача оптимизации

Задачей оптимизации в математике называется задача о нахождении экстремума (минимума или максимума) вещественной функции в некоторой области. Как правило, рассматриваются области, принадлежащие и заданные набором равенств и неравенств.

Содержание

Постановка задачи оптимизации

Для того, чтобы корректно поставить задачу оптимизации необходимо задать:

Тогда решить задачу 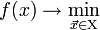означает одно из:

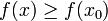
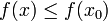
Если минимизируемая функция не является выпуклой, то часто ограничиваются поиском локальных минимумов и максимумов: точек x₀ таких, что всюду в некоторой их окрестности для минимума и для максимума.

Если допустимое множество 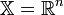, то такая задача называется задачей безусловной оптимизации, в противном случае — задачей условной оптимизации.

Классификация методов оптимизации

Методы, по средством которых решают задачи оптимизации, подразделяются на виды, соответствующие задачам, к которым они применяются:

Существующие в настоящее время методы поиска можно разбить на три большие группы:

Некоторые детерминированные методы:

Помимо того, оптимизационные методы делятся на следующие группы:

Также они разделяются по критерию размерности допустимого множества на методы одномерной оптимизации и методы многомерной оптимизации.

Литература

Ссылки

Методы второго порядка:
(требуют значения первой и второй частных производных):
Метод Ньютона • Метод Ньютона-Рафсона

Полезное

Смотреть что такое «Задача оптимизации» в других словарях:

задача оптимизации надёжности — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN reliability optimization problem … Справочник технического переводчика

Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия

Задача о рюкзаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия

Задача о рюказаке — Задача о ранце (рюкзаке) одна из задач комбинаторной оптимизации. Название это получила от максимизационной задачи укладки как можно большего числа нужных вещей в рюкзак при условии, что общий объём (или вес) всех предметов ограничен. Подобные… … Википедия

Задача о коммивояжере — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача о коммивояжёре — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача коммивояжера — Задача коммивояжёра (коммивояжёр бродячий торговец) является одной из самых известных задач комбинаторной оптимизации. Задача заключается в отыскании самого выгодного маршрута, проходящего через указанные города хотя бы по одному разу с… … Википедия

Задача коммивояжёра — Оптимальный маршрут коммивояжёра через 15 крупнейших городов Германии. Указанный маршрут является самым коротким из всех возможных 43 589 145 600. Задача коммивояжёра (англ. Travelling salesman problem, TSP) (коммивояжёр&#16 … Википедия

Задача о ранце — Пример задачи о ранце: необходимо разместить ящики в рюкзак при условии на вместимость рюкзака 15 кг, так чтобы суммарная полезность предметов в рюкзаке была максимальной. Задача о ранце (рюкзаке) (англ. … Википедия

Задача о максимальном потоке — Максимальный поток в транспортной сети. Числа обозначают потоки и пропускные способности. В теории оптимизации и теории графов, задача о максимальном потоке заключается в нахождении такого потока по транспортной сети, что сум … Википедия

Источник

Оптимизационные задачи. Общие сведения

Оптимизационные задачи. Общие сведения

Оптимизационная задача – это задача нахождения экстремума (минимума или максимума) целевой функции в некоторой области конечномерного векторного пространства, ограниченной набором линейных и/или нелинейных равенств и/или неравенств.

Целевая функция представляет собой набор критериев качества, которые должны быть оптимизированы одновременно. В общем случае целевая функция состоит из управляемых и неуправляемых переменных. Условие поиска экстремума целевой функции записывается в следующем виде:

Методы решения оптимизационных задач изучает математическое программирование. Математическое программирование – это математическая дисциплина, изучающая теорию и методы решения задач по определению экстремумов функций на множествах конечномерного векторного пространства, определяемых набором линейных и/или нелинейных ограничений (равенствами и/или неравенствами). Математическое программирование представляет собой, как правило, многократно повторяющуюся вычислительную процедуру, приводящую к искомому оптимальному решению. Выбор метода математического программирования для решения оптимизационной задачи определяется видом зависимостей в математической модели, характером искомых переменных, категорией исходных данных и количеством критериев оптимальности:

Решение задачи оптимизации осуществляется с помощью поисковых методов, использующих предшествующую информацию для построения улучшенного решения задачи (итерационные методы расчета). К настоящему времени разработано достаточно много методов локальной оптимизации для решения задач общего вида. Большинство из них используют принцип локального спуска, когда метод последовательно на каждом шаге переходит к точкам с существенно меньшими (большим) значениями целевой функции. Данные методы отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, а также критериями окончания поиска. Поиск оптимального значения в таких задачах может быть представлен в виде итерационного соотношения:

где переменная — это приращение вектора управляемых параметров. В зависимости от условия поиска (поиск максимального или минимального значения целевой функции) используется либо знак «+», либо знак «-».

Приращение вектора управляемых параметров в большинстве случаях вычисляется по формуле:

В данном выражении — значение вектора управляемых параметров на k-ом шаге, — шаг расчета, а — направление поиска экстремума функции.

В зависимости от числа управляемых параметров различают методы одномерной и многомерной оптимизации (многокритериальная оптимизация). Поиск считается одномерным, в случае если аргументом целевой функции является один управляемый параметр.

Шаг расчета

Итерационная форма методов локальной оптимизации для решения задач поиска экстремума целевой функции требует выбора шага расчета вдоль заданных направлений на каждом шаге итерации. Шаг расчета может быть постоянным или переменным, но оптимальное значение длины шага определяется в результате поиска экстремума целевой функции в выбранном направлении с использованием методов одномерной оптимизации:

Другими словами, величина шага расчета вычисляется при решении следующего выражения:

В результате решения данного уравнение мы получим, что шаг расчета в символьном виде определяется следующим образом:

где — значение аргумента функции на k-ом шаге итерации;

n – количество неизвестных переменных, которые определяются в ходе решения задачи;

L – некоторая константа, которая определяется из определителя следующей матрицы:

В результате для определения оптимального шага расчета требуется выполнить большой объем вычислений целевой функции. Для снижения числа операций на практике используют другой подход: подбирают такие значения шага расчета , чтобы они удовлетворяли любому из представленных ниже условию.

где коэффициент , а шаг расчета определяется итеративно путем умножения первоначального шага на коэффициент до тех пор пока не будет выполняться условие.

Рис.1. Критерий выбора шага расчета по правилу Армихо

Методика определения шага расчета оптимизационной задачи в соответствии с правилом Армихо заключается в следующем:

1.Задать коэффициент в диапазоне от 0 до 1.

2.Задать начальное значение шага .

Процедура поиска (проверка выполнения условия по правилу Армихо)

3. В случае если условие по правилу Армихо не выполняется, тогда необходимо скорректировать шаг расчета , где переменная может принимать любое значение от 0 до 1, по умолчанию примем, что переменная , а — текущий шаг поиска.

4. В случае если условие по правилу Армихо выполняется, тогда в качестве шага расчета можно принять , а процедура поиска завершается.

Данное правило требует однократного вычисления градиента, после чего небольшое количество итераций затрачивается на подбор подходящего шага. Каждая из таких вложенных итераций, в свою очередь, требует вычисления значения целевой функции без градиента, то есть проводимые испытания относительно легковесны. Следует отметить, что данное условие удовлетворяется для всех достаточно малых . Правило Армихо можно расширить на многокритериальный случай: неравенство 3.19 следует понимать покомпонентно.

— функция не должна превышать значения некоторой убывающей линейной функции, равной в нуле:

— величина скорости изменения функция в заданном направлении была в раз больше, чем скорость изменения функции в первоначальной точке

Рис.2. Критерий выбора шага расчета по правилу Вольфе-Пауэлла

Методика определения шага расчета оптимизационной задачи в соответствии с правилом Вольфе-Пауэлла заключается в следующем:

1. Задать коэффициент и в диапазоне от 0 до 1 .

2. Задать начальное значение шага , принять коэффициент и

Процедура поиска (проверка выполнения условия по правилу Вольфе-Пауэлла)

3. В случае если первое условие по правилу Вольфе-Пауэлла не выполняется, тогда принять коэффициент . Перейти к пункту №5.

4. В случае если второе условие по правилу Вольфе-Пауэлла не выполняется, тогда принять коэффициент :

— в случае если , то перейти к пункту №5;

— в случае если выполнить экстраполяцию, положив , где r – коэффициент экстраполяции . Перейти к пункту №3.

5. Выполнить текущий расчет шага по формуле

где — коэффициент интерполяции, который определяется в следующем диапазоне

Перейти к пункту №3.

6. В случае если выполняются оба условия правилу Вольфе-Пауэлла, тогда в качестве шага расчета можно принять , а процедура поиска завершается.

Методика определения шага расчета оптимизационной задачи в соответствии с правилом Голдстейна-Армийо заключается в следующем:

1.Задать коэффициент и в диапазоне от 0 до 1 .

2. Задать начальное значение шага

3. В случае если условие по правилу Голдстейна-Армийоне выполняется, тогда необходимо скорректировать шаг расчета , где переменная может принимать любое значение от 0 до 1, по умолчанию примем, что переменная , а — текущий шаг поиска.

Критерии останова оптимизационного процесса

Поиск оптимального решения завершается в случае, когда на итерационном шаге расчета выполняется один (или несколько) критериев:

— траектория поиска остается в малой окрестности текущей точки поиска:

— приращение целевой функции не меняется:

— градиент целевой функции в точке локального минимума обращается в нуль:

Классификация методов оптимизации.

В настоящее время для решения задач оптимизации разработано огромное количество различных математических методов. Применение того или иного метода определяется постановкой задачи, сложностью вычисления функции и ее производных, поведением функции и т. д.

Задачи оптимизации и методы их решения можно разделить по наличию или отсутствию ограничений (задаётся системой неравенств и равенств или более сложным алгоритмом) в математических моделях на методы условной и безусловной оптимизации. Для реальных задач характерно наличие ограничений, однако методы безусловной оптимизации также представляют интерес, поскольку задачи условной оптимизации с помощью специальных методов могут быть сведены к задачам без ограничений.

Методы безусловной оптимизации

Классическая задача безусловной оптимизации формулируется следующим образом: требуется найти вектор переменных , при котором целевая функция принимает экстремальное (максимальное или минимальное значение) значение

Экстремальное значение целевой функции соответствует оптимальному управлению. В графическом виде постановка задачи выглядит следующим образом:

Рис.3. Задача безусловной оптимизации для функции двух переменных

Сущность метода оптимизации в первую очередь определяется способом выбора направления движения к экстремуму. В зависимости от используемого порядка производных целевой функции методы безусловной оптимизации делят на методы нулевого, первого и второго порядков. Если производные не используются, то имеет место метод нулевого порядка, если используются первые или вторые производные, то соответственно метод первого или второго порядка.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач нулевого порядка:

Методы одномерного поиска:

— Метод дихотомического деления и метод золотого сечения – это методы одномерной оптимизации, основанные на делении отрезка, на котором ищется экстремум, пополам или в пропорциях золотого сечения (0,382 / 0,618), соответственно.

— Метод полиномиальной аппроксимации (метод квадратичной интерполяции) – это метод одномерной оптимизации, в соответствии с которым целевая функция аппроксимируется квадратичным полиномом.

Методы многомерного поиска:

— Метод покоординатного спуска (Гаусса-Зейделя) – это метод безусловной оптимизации нулевого порядка, в котором направления поиска выбираются поочередно вдоль всех координатных осей, шаг рассчитывается на основе одномерной оптимизации.

— Метод вращающихся координат (Метод Розенброка) – это метод безусловной оптимизации нулевого порядка, в котором реализуется покоординатный спуск, но вдоль координатных осей, поворачиваемых таким образом, чтобы направление одной из осей было близко к направлению, параллельному дну оврага.

— Симплексный метод (метод деформируемого многогранника или метод Нелдера-Мида) – это метод безусловной оптимизации нулевого порядка, основанный на многократно повторяемых операциях построения многогранника с (n+1) вершинами, где n — размерность пространства управляемых параметров, и перемещения наихудшей вершины (с наихудшим значением целевой функции) в направлении центра тяжести многогранника.

Градиент в базовой точке строго ортогонален к поверхности, а его направление показывает направление наискорейшего возрастания функции, а противоположное направление (антиградиента), соответственно, показывает направление наискорейшего убывания функции. Градиентные методы отличаются один от другого способом определения направления движения к оптимуму, размером шага и продолжительностью поиска вдоль найденного направления, а также критериями окончания поиска.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач первого порядка:

— Метод градиентного спуска – это метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента с переменным (дробным) шагом, который задается пользователем.

— Метод наискорейшего спуска – это метод нахождения локального минимума (максимума) функции при движении вдоль градиента с оптимальным шагом. Шаг расчета выбирается минимума целевой (минимизируемой) функции в направлении спуска.

— Метод сопряженных градиентов (метод Флетчера-Ривса) – это метод безусловной оптимизации первого порядка, в котором направление поиска на очередном шаге есть градиентное направление, скорректированное с учетом направления поиска на предыдущем шаге.

— Метод переменной метрики (метод Девидона-Флетчера-Пауэлла) – это метод безусловной оптимизации, в котором за основу взято решение системы уравнений, выражающих необходимые условия экстремума.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач второго порядка:

— Метод Ньютона – это метод безусловной оптимизации, основанный на использовании необходимых условий безусловного экстремума целевой функции: равенству нулю первой производной. В соответствии с данным методом определяют матрицу вторых частных производных целевой функции по управляемым параметрам (матрицу Гессе).

— Метод Марквардта – это метод безусловной оптимизации, направленный на решение задач о наименьших квадратах. Является альтернативой методу Гаусса – Ньютона. Может рассматриваться как комбинация последнего с методом градиентного спуска или как метод доверительных интервалов.

Методы условной оптимизации

Классическая задача условной оптимизации формулируется следующим образом: необходимо найти вектор переменных , при котором целевая функция принимает экстремальное (максимальное или минимальное значение) значение

при заданных условиях (равенствами и/или неравенствами), при этом число ограничений m может быть как больше, так и меньше числа переменных n.

, j=1,2,…,m.

Другими словами, необходимо найти экстремум целевой функции при условии, что значения аргументов функции принадлежат области допустимых значений, которая образуется системой ограничений. Экстремальное значение целевой функции соответствует оптимальному управлению. В графическом виде постановка задачи выглядит следующим образом:

Рис.4. Задача условной оптимизации для функции двух переменных

В зависимости от используемого метода решения методы условной оптимизации можно разделить на методы сведения задачи к безусловной оптимизации и методы непосредственного решения.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач условной оптимизации:

— Метод неопределенных множителей Лагранжа – это метод условной оптимизации, ориентированный на поиск экстремума целевой функции при наличии ограничений типа равенств.

— Условия Куна-Таккера – это метод решения оптимизационной задачи математического программирования с заданными ограничениями. Метод является обобщением метода множителей Лагранжа на случай общей задачи нелинейного программирования с ограничениями, как в виде равенств, так и в виде неравенств.

— Метод штрафных функций – это метод или группа методов для решения задач математического программирования, основанные на преобразовании задачи условной оптимизации в задачу безусловной оптимизации путем формирования новой целевой функции, учитывающей ограничения задачи.

Наиболее популярными (с точки зрения обучения в высшей школе) являются следующие методы решения оптимизационных задач условной оптимизации:

— Метод приведенного градиента – это метод условной оптимизации, ориентированный на решение задач с ограничениями типа равенств. Направление движение в данном методе определяет приведенный градиент функции.

Численные методы оптимизации реализованы и широко используются в различных математических пакетах. При этом наличие готовых программных средств (математических библиотек и пакетов) не только не снимает необходимость изучения методов, а наоборот, делает подготовку в этом направлении еще более актуальной. Это связано с тем, что при решении реальной задачи от специалиста требуется грамотная математическая постановка задачи, ее формализация, обоснование и выбор наиболее эффективного метода расчета, а также умение производить оценку адекватности и точности полученных результатов.

Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.

Источник