Что такое орнамент в геометрии

Геометрический орнамент

Становление геометрического орнамента

Геометрически орнамент возник задолго до появления текстиля, керамики, металлических предметов быта и орудий труда и каких бы то ни было рукотворных архитектурных сооружений. Как украшения для этих форм он стал использоваться по мере их изобретения. В большинстве случаев орнамент при этом выполнял не столько функцию украшения, сколько нес сакральный мистический смысл. Одним из самых первых распространившихся повсеместно элементов орнамента стал ромб. Так же достаточно часто использовался ромбо-меандровый орнамент. Данный геометрический элемент можно считать структурообразующим. Именно ромб лежит в основе орнамента в целом.

В качестве примера можно привести найденные на территории России костяные фигурки Матери-прародительницы, относимые к эпохе палеолита, декорированными именно ромбическим орнаментом. Женщины того времени на празднествах украшали себя именно таким узором. Постепенно он стал символом именно плодородия, удачи и процветания. Палеонтологом В. И. Бибиковой было убедительно доказано, что ромб и волнообразные линии, часто сопровождающие его, являются ничем иным, как воспроизведением узора мамонтовой кости. Раскопки показали, что такой орнамент использовался повсеместно, начиная от неолита и до бронзового века. Вплоть до гальштатской эпохи он помещался в основном на ритуальных предметах и жертвенниках.

Во время неолита к ромбо-меандровому орнаменту добавляются спирально-змеиный и линейно-струйчатый. Для этого периода характерны вертикальные линии, волнистые либо прямые, символизирующие дождь. Часто композицию дополняли клубки сплетшихся змей. Важным этапом в становлении орнамента считается возникновение геоцентрической идеи. Именно она стала символом завершения человеком познания мира. Изображения коловрата встречаются, например, на русских прялках, прославянских сосудах, в русских народных костюмах и т.д. Чаще всего «колесо Юпитера» изображалось с шестью спицами. Широко использовался этот орнаментальный элемент и в резьбе. В данном случае он носил название «громового знака». Все основные виды геометрического орнамента полностью сложились уже к I в до н. э. За прошедшие столетия этот вид декора изменений практически не претерпел. Если сравнить, например, орнаменты фабричных тканей XVIII – XX века с древними декорами, особой разницы заметить нельзя.

Арабский геометрический орнамент

В историю арабский геометрический орнамент вошел под названием «гирих» (араб. – «узел»). Мотивом восточного декора часто становилась плотно связанная орнаментальная сетка. В основе гириха лежит разделенный на части круг. Таким образом, происходит построение всех других фигур – треугольника, прямоугольника, многоугольника и т.д. Такое композиционное решение позволяет создавать симметричные мотивы. Любой геометрический орнамент всегда математически правилен и может быть разделен на равные части. Особенностью арабского гириха является некоторый отход от этой точности, предоставляющей художнику больший простор для творчества.

Создание бесконечного орнамента состоит из следующих основных этапов:

• выбор определений раппортной системы;
• построение отдельных мотивов;
• размещение их на сетке;
• выбор способа исполнения (зависит от материала).

Художественная сторона в орнаментах напрямую связана с четвертым этапом, то есть находиться в полностью зависимости от того, на каком предмете будет выполняться декор. Еще одной особенностью именно арабского узора является получения очень сложных геометрических систем всего лишь из одного мотива. О сложности орнаментов говорит, например, то, что уже в XVIII веке восточные художники умели гармонично сочетать двенадцатиконечные звезды с пятиконечными.

Источник

Геометрический орнамент

Геометрический орнамент формирует линейные, пространственные композиционные системы. Именно геометрический орнамент дает возможность постичь суть математического, рационального «объяснения» окружающего мира. Создавая разнообразные композиции, состоящие из центрических, квадратных, треугольных сегментов, художник опирался на исходные положения построения геометрического орнамента— математический расчет. Во главу угла ставилось число, которое в орнаментальной композиции кратно повторялось или выражало про-порциональное соотношение компонентов.

Основой геометрического орнамента являлась строгая последовательность и упорядоченность в использовании одних и тех же элементов. Чаще всего орнаментальные композиции, вводящие в себя геометрические элементы, выстраивались по законам симметрии. Однако встречались и более сложные варианты орнаментальных комбинаций, насыщенные растительными, тератологическими (звериными), гротескными сюжетами. Как правило, геометрические мотивы повторялись или чередовались, образуя непрерывный ритмический ряд единообразных сегментов.

Важной стороной изучения геометрического орнамента является не только выявление структуры и композиционных особенностей, но и раскрытие семантического толкования отдельных его составляющих.

Некоторые исследователи утверждают, что геометрический орнамент возник в первобытную эпоху и выражал некую абстрактную идею. Древний человек своеобразно отражал свои представления об окружающем мире с помощью знаков, изображаемых на различных бытовых предметах и на стенах пещер.

В первобытных орнаментальных композициях часто встречаются изображения геометрических фигур-символов: круга-солнца, квадрата- земли, треугольников-гор (или леса); спирали, выражающей идеи бес-конечности бытия, постоянного развития или вечного движения.

В каждой значимой культовой системе — языческой, христианской, буддийской, индуистской, мусульманской и других — появлялись собственные парадигмы, определявшие семантику геометрических фигур в орнаментальных композициях.

Хотя многие исследователи склонны видеть в геометрическом орнаменте проявление первобытно-общинных алгоритмов, каждая культура по-своему интерпретировала тот или иной знак.

Круг, не имеющий начала и конца, бесконечный и всеобъемлющий, являлся универсальным символом. Во многих традициях круг олицетворял солярный культ, представлял собой вселенское пространство, Космос. Иногда другие изображения — яйцо, черепаха, диск, часы — имели ту же смысловую нагрузку, отражали космогоническую сущность круга.

Основная функция круга (или шара) — символически изобразить небесные тела. В мировой художественной практике круг был непременным атрибутом египетского бога солнца Атона. Крылатый диск помещался над головой могущественного божества. Примером тому могут служить солнечная колесница Аполлона, колесницы индийских божеств. Перуанский бог Солнца изображался с лицом в виде золотого круга, китайской аналогии Неба. В христианском культе круг связан с понятием мира и бесконечности, небесного сияния, небесной сферы и т. п., у мусульман круг — это всевидящее око Аллаха.

Квадрат являлся основой орнаментального декора многих древних культур — Древней Индии, Америки, Китая, Греции; широко использовался мастерами-мозаичистами в Средние века. В соответствии с древними представлениями квадрат символизировал основы мироздания, т. е. четыре стороны света. Все углы квадрата (ромба) соотносились и с территориальными представлениями. Индейцы Северной Америки пуэбло, когда «указывали» направление, употребляли цветовое значение и направление, апеллируя при этом к квадратной форме. Квадрат (иногда прямоугольник) служил также обозначением пахотной земли, являясь ключевой фигурой земледельческого культа. Квадрат, заполненный внутри точками или линиями, обозначал у славянских племен засеянное поле. У китайцев прямоугольный блок «цзун» с отверстием внутри, как и узор из перекрещивающихся ромбов, символизировал богатую урожаем землю. В греко-римской традиции квадрат являлся символом Афродиты, воплощавшей женскую, плодородную силу.

Зигзагообразный и спиралевидный мотивы, часто встречавшиеся на бытовых и культовых предметах Греции, доколумбовой Америки, Китая, Индии, африканских племен условно обозначали либо море, либо молнию (у китайцев этот узор носил название «лэй вэнь»). Именно гроза (молния) символизировала появление Небесного дракона— покровителя воды и небесно-водных стихий. Спиралевидный орнамент являл собой как бы прототип движения некоторых небесных тел.

Появление треугольника связывали с магическим числом три или триединством понятий. В христианстве и иудаизме равносторонний треугольник вершиной вверх был знаком высшего божества. В средние века треугольник воспринимался как олицетворение Троицы: Бог Отец, Бог Сын и Бог Дух Святой. В древнекитайской традиции треугольник — почти всегда символ женского начала.

Одним из самых мистический и распространенных геометрических элементов по праву считался крест. До сих пор поражает воображение исследователей многообразие форм креста.

Разнообразные комбинации вышеперечисленных символов в искусстве орнамента подчас призваны раскрыть сакральный смысл предмета, его предназначение или применение. Но если рассматривать геометрический орнамент вне зависимости от его аллегорически- символического значения, то становится ясно, что художник часто преследовал чисто художественную цель — украсить предмет.

Мастера Древнего Египта (III тыс. до н. э. — VII в. до н.э.), кроме излюбленного стилизованного растительного декора, вплетали в канву орнамента и геометрические элементы — волнообразные линии, шашечный узор, сетки, точки. Интересен тот факт, что прототипом христианского креста, принятого коптской церковью в качестве своей эмблемы, был древнеегипетский анкх — символ бессмертия. В силу этнокультурных традиций, сложившихся в долине Нила, геометрические мотивы только дополняли основные композиционные решения.

В Индии в эпоху Гуптов (IV в. до н. э.) особую популярность приобрели орнаменты в виде чередующихся ромбов и кругов. С распространением буддийского культа храмы и культовые предметы стали украшаться розетками, вписанными в круги и квадраты. В керамических изделиях также появлялись геометрические мотивы, но вскоре их вытеснил растительный декор. Самыми примечательными были индийские ткани, украшенные всевозможными орнаментами, среди которых преобладали ромбы, квадраты, зигзаги.

Индейцы, населявшие территории Северной и Южной Америки (до XVIII в.), прославились керамическим ремеслом и ткачеством. Гончарные изделия, столь необходимые в повседневной жизни, декорировались всевозможными магическими символами — треугольниками, кругами, спиралями, зигзагами. Средневековых европейцев местные ткани поражали удивительной лаконичностью и сочностью узора. Орнаментальные композиции древних ацтеков, инков, майя, пуэбло, лакота и многих других отражали трепетное отношение к окружающему миру, запечатленному языком простейших геометрических фигур.
Особой красотой отличались орнаментальные построения Древней Греции (VII в. до н. э. — III в. н. э.). Меандр — зигзагообразный мотив — очевидно, олицетворял вечность движения, бесконечность повторения. Лента орнамента строго подчинялась форме, при этом не нарушалась целостность восприятия. Даже многокрасочные мозаичные полы отличались сдержанностью и простотой геометрических узоров. В искусстве мозаики греко-римским мастерам не было равных. Они искусно воспроизводили пространственную глубину так, что зрителю казалось, будто он идет по рельефному полу. Опыт античных художников был органически воспринят Византийской Империей (IV—XIV вв.).

Источник

геометрический орнамент

Смотреть что такое «геометрический орнамент» в других словарях:

Геометрический стиль — Геометрический стиль. Аттическая амфора. 2 я четверть 8 в. до н.э. ГЕОМЕТРИЧЕСКИЙ СТИЛЬ, одна из ранних стадий (9 8 вв. до нашей эры) развития древнегреческого искусства. Наиболее ярко проявился в вазописи, отчасти в мелкой пластике и глиптике:… … Иллюстрированный энциклопедический словарь

ГЕОМЕТРИЧЕСКИЙ — ГЕОМЕТРИЧЕСКИЙ, геометрическая, геометрическое (научн.). 1. прил. к геометрия. Геометрическая теорема. Геометрические тела (шар, конус, пирамида, призма и др.). Геометрические фигуры (треугольник, квадрат, круг и др.). 2. Состоящий из линий,… … Толковый словарь Ушакова

ГЕОМЕТРИЧЕСКИЙ СТИЛЬ — в искусстве ранняя (9 8 вв. до н. э.) стадия развития древнегреческого искусства: геометрический орнамент, геометризованные фигуры людей и животных в вазописи, схематичные бронзовые статуэтки … Большой Энциклопедический словарь

Геометрический стиль — Гидрия в стиле геометрики. 750 700 гг. до н. э. Лувр … Википедия

геометрический стиль — в искусстве, ранняя (IX VIII вв. до н. э.) стадия развития древнегреческого искусства: геометрический орнамент, геометризованной фигуры людей и животных в вазописи, схематичные бронзовые статуэтки. * * * ГЕОМЕТРИЧЕСКИЙ СТИЛЬ ГЕОМЕТРИЧЕСКИЙ СТИЛЬ… … Энциклопедический словарь

Орнамент — на здании … Википедия

Орнамент — исполненное в одной плоскости, выделенное рельефно илирезанное вглубь, одноцветное или иллюминованное красками изображение,служащее в архитектуре украшением различных частей зданий (полов,потолков, карнизов, фризов, капителей колонн, самых стен и … Энциклопедия Брокгауза и Ефрона

ОРНАМЕНТ — (от латинского ornamentum украшение), узор, состоящий из ритмически упорядоченных элементов для украшения каких либо предметов и архитектурных сооружений. Зачатки орнамента в искусстве палеолита, большого разнообразия форм орнамент достиг в… … Современная энциклопедия

Орнамент — (от латинского ornamentum украшение), узор, состоящий из ритмически упорядоченных элементов для украшения каких либо предметов и архитектурных сооружений. Зачатки орнамента в искусстве палеолита, большого разнообразия форм орнамент достиг в… … Иллюстрированный энциклопедический словарь

Источник

Учебный проект» Геометрия орнаментов и узоров»

Учебный проект» Геометрия орнаментов и узоров» выполнила ученица 9б класса Стекачева

Восхищаясь рукотворной красотой орнаментов, воплощенных в предметах декоративно-прикладного искусства, коврах, паркетах, гобеленах, вышивке и даже искусства уличного граффити — мы задумались о роли геометрии в создании этих произведений. Каждому человеку понятны принципы красоты. Но почему-то некоторым людям кажется, что они неспособны эту красоту воспроизвести. Математика может помочь в этом изящном искусстве и желании сделать красоту самому.

Просмотр содержимого документа
«Учебный проект» Геометрия орнаментов и узоров»»

Муниципальное общеобразовательное учреждение

«Средняя общеобразовательная школа №15

с углубленным изучением отдельных предметов

имени Героя Советского Союза

Расковой Марины Михайловны »

Энгельсского муниципального района Саратовской области.

Проектная работа по теме: «Геометрия орнаментов и узоров»

Выполнила ученица 9б класса Стекачёва Елизавета

Руководитель: учитель математики Затеева Валентина Павловна

Геометрия орнамента в Древнем Египте

Орнаменты в Древнем Египте

Геометрия орнамента в Древней Греции

Орнаменты в Древней Греции

Геометрия орнамента в Древней Руси

Орнаменты в Древней Руси

Мозаика Пенроуза и древние исламские узоры

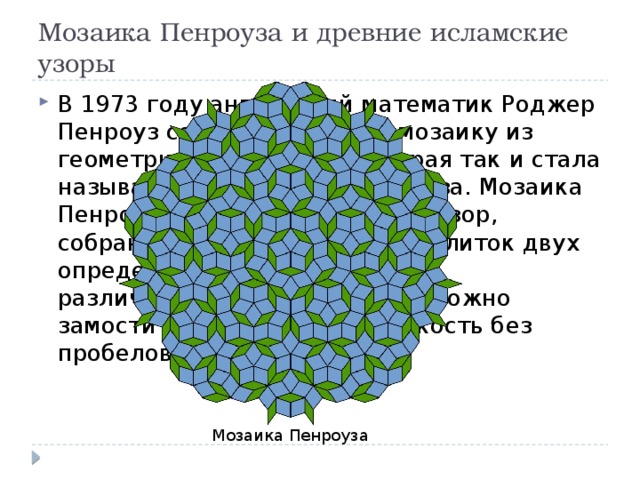
Мозаика Пенроуза и древние исламские узоры

Мозаика Пенроуза и древние исламские узоры

Мозаика Пенроуза и древние исламские узоры

Мозаика Пенроуза и древние исламские узоры

Источник

Что такое орнамент в геометрии

Оглядись, посмотри, как красиво –

Из орнаментов разных узор

На обоях, ковре. Белый с синим

На клеёнке штришками «забор»,

Разрисован и бабушкин фартук,

И на мамином сереньком платье

На кайме ярко стразы горят.

Кружева на салфетках, накидках

Составляют цветочный набор,

А на стёкла зимою налипнет

Из снежинок и льдинок узор.

Актуальность. Восхищаясь рукотворной красотой орнаментов, воплощенных в предметах декоративно-прикладного искусства, коврах, паркетах, гобеленах, вышивке и даже искусства уличного граффити — мы задумались о роли геометрии в создании этих произведений. Каждому человеку понятны принципы красоты. Но почему-то некоторым людям кажется, что они неспособны эту красоту воспроизвести. Математика может помочь в этом изящном искусстве и желании сделать красоту самому.

Объект исследования: орнаменты и узоры.

Предмет исследования: произведения искусства (картины, паркеты, ковры, часы), математика.

Цель исследования: изучение математических закономерностей, связанных с орнаментами и паркетами, а именно ответить на следующие вопросы:

-Какие геометрические преобразования лежат в основе создания таких орнаментов?

— Как построить измельчающие узоры?

Методы исследования:

— поисковый, аналитический, сравнения, наблюдения

Задачи:

1) Познакомиться с историей возникновения узоров.

2) Применить знания на практике, создав орнамент на основе изученных закономерностей.

3) Показать важность математических закономерностей.

Гипотеза: предполагаем, что роль математики в построении узоров очень велика. Сложность узора зависит от теоретических знаний человека, который рисует его.

Глава 1.1. Геометрия орнамента

Орнамент (от лат. ornamentum — украшение) — это узор, состоящий из повторяющихся, ритмически упорядоченных элементов.

Орнамент предназначен для украшения различных предметов (посуды, мебели, текстильных изделий, оружия) и архитектурных сооружений

Приложение 1. Связанный с поверхностью, которую он украшает и зрительно организует, орнамент, как правило, выявляет и подчеркивает своим построением, формой и цветом архитектурные и конструктивные особенности предмета, природную красоту материала.

В построении орнамента используют главным образом принцип симметрии. Рассматривая разные композиции, легко увидеть, что орнамент можно продолжать в разные стороны, даже если его первоначальная композиция ограничена и замкнута.

В народном творчестве, где орнамент нашел наибольшее распространение, постепенно складывались устойчивые формы и принципы построения орнамента, во многом определившие национальные, художественные традиции разных народов.

Слово «меандр» происходит от названия очень извилистой реки в Малой Азии. Ныне она называется Большой Мендерес. Орнамент меандр как будто повторяет излучины этой прихотливой реки. Акант — это род травянистого растения, распространенного в Средиземноморье. У него большие листья, красиво изогнутые стебли. В обоих этих орнаментах греки предстают перед нами прилежными учениками природы, которой они поклонялись. Они умели рассказать словами, вылепить из глины, вытесать из мрамора прекрасную сказку про каждый холм, каждую речку, каждый лист.

Не будет преувеличением сказать, что нигде орнаментальное искусство не достигло такого расцвета и совершенного воплощения, как на мусульманском Востоке. Для него характерно сочетание геометрических и растительных мотивов, так как Кораном было запрещено изображение людей и животных.

Впоследствии, распространившись по Европе, этот вид орнамента получил название «арабеска» (от ит. arabesco — арабский). В исламских странах арабеску представлял узор. На первый взгляд мы видим повторения, диктуемые симметрией, но это только самые крупные элементы орнамента- Приложение 1.

Высокого развития орнамент достиг в средневековой Руси. Для русского орнамента характерны как геометрические и растительные формы, так и изображения птиц, зверей, фантастических животных и человеческих фигур. Наиболее ярко русский орнамент выражен в резьбе по дереву и в вышивке. В плоском орнаменте одним из наиболее часто используемых мотивов является так называемая плетенка — различного вида переплетения полосок типа лент, ремней, стеблей цветов-Приложение 1.

По сути, именно это открытие побудило в конце XIX века физиков и математиков подробнее изучить орнаменты (тогда и было дано точное математическое определение орнамента).

Глава 1.2. Геометрия в орнаменте

Анализируя некоторые орнаменты, можно наблюдать примеры применения в них геометрических построений. Например, деление окружности на равные части, сопряжения, применение циклоид, параллельных астроид и завитков.

Изучая орнаменты от самых древних до современных, можно заметить, что с течением времени менялось их содержание, но композиционный строй, его ритмическая основа оставались неизменными. В композиции орнамента присутствует математическая основа. Особую роль играют симметрия и разбиение плоскости на равные фигуры. Преобладающее большинство орнаментов построено на основе строгой математической логики.

Перечислим виды геометрических орнаментов, ограничиваясь главным и идя от простого к сложному. Приведенные нами примеры немногочисленны, и их легко умножить.

Прежде всего назовем точку, которая мало значит сама по себе, но при повторении дает декоративный эффект, успешно использованный в искусстве Ирана и в китайских изделиях Танского периода.

Затем идет линия или лента, широко применявшаяся для того, чтобы разграничить отдельные мотивы. Линию можно увидеть и в доисторических орнаментах и на греческих вазах (геометрический и классический стили).

Квадрат, прежде всего, ограничивает поверхности, заполненные мотивами, как мы это видим, например, на кессонированных потолках эпохи Возрождения.

Ромб можно увидеть на множестве доисторической гончарной посуды и на китайских бронзовых изделиях периода Шан; он также служит для ограничения декорируемых поверхностей. То же можно сказать и о шашечном орнаменте, который широко используется в узорах тканей со времен Древнего Египта вплоть до современного искусства.

Треугольник служит орнаментальным мотивом для мозаичных полов и для тканей.

Шестиугольник и восьмиугольник, и их сочетания широко воспроизводились в декоративном искусстве стран ислама.

Среди кривых линий назовем в первую очередь синусоиду, волнообразную ленту, которая встречается как обрамление и в романском, и в китайском искусстве.

Спираль снискала большой успех и огромное распространение; она характерна для Эгейской, а затем и для микенской культур.

Часто и в самых разных странах применяется мотив круга, использовавшийся как собственно орнаментальный элемент, например на кипрских гончарных изделиях, так и для ограничения поверхности, заключающей в себе другие мотивы, как, например, на японских гербах.

Линейные орнаменты называются бордюрами.

БОРДЮР – это периодически повторяющийся рисунок на длинной ленте. Бордюры используются в настенных росписях, в чугунном литье для оград, мостов, набережных. Рисунки в виде бордюров наносятся на ткани, мебель, обои и т.д.

Любой бордюр может быть совмещён сам с собой параллельным переносом. При рисовании бордюров кроме параллельного переноса используется симметрия относительно прямой, и центральная симметрия.

Математические принципы построения бордюров:

а) параллельный перенос;

б) зеркальная (осевая) симметрия с вертикальной осью;

в) зеркальная (осевая) симметрия с горизонтальной осью;

г) поворотная (центральная) симметрия.

Всего существует семь типов симметрии бордюров:

а) В простейшем случае симметрия бордюра полностью исчерпывается переносной симметрией вдоль оси.

б) Бордюры обладают наряду с переносной также зеркальной симметрией. Здесь ось переноса является также осью симметрии.

в) У бордюров ось переноса является осью скользящего отражения.

г) Бордюры имеют вертикальные оси симметрии. Эти оси изображены на рисунке в виде отрезков прямых, перпендикулярных к оси переноса.

д) Бордюры обладают переносной симметрией и поворотной симметрией (центральной).

е) Бордюры обладают переносной симметрией, центральной симметрией и осевой симметрией относительно вертикальной оси.

ж) Бордюры, основанные на комбинировании зеркальных отражений. Такие бордюры имеют наряду с вертикальной также горизонтальные оси симметрии.

Рисунок бордюра получается, когда мы начинаем геометрически перемещать его элемент. Любой бордюр может быть совмещен сам с собой параллельным переносом. При рисовании бордюров используются, кроме параллельного переноса, симметрия относительно прямой и центральная симметрия (симметрия относительно точки).

Для построения линейных орнаментов (бордюров) нужно начать с построения его ячейки: также придумывают узор (трафаретку), потом с помощью параллельного переноса переносят узор на длину вектора (направленного отрезка) влево или вправо во столько раз, сколько нужно.

Глава 1.3. Построение орнаментов на компьютере

Основной принцип построения орнаментов в компьютерных программах – это отражение одного изображения в разные стороны.

«Рисунок» > «Отразить/повернуть» > «Отразить слева направо», «Отразить сверху вниз», «Повернуть на угол…»

Орнамент первого типа. Для его построения рисуем фрагмент, затем используем параллельный перенос.

Орнамент второго типа. Используем параллельный перенос и осевуюсимметрию (относительно горизонтальной оси).

Орнамент третьего типа. Используется композиция преобразований: осевая симметрия фрагмента относительно горизонтальной оси, параллельный перенос «нижней» части орнамента на вектор a/2, параллельный перенос получившегося рисунка на вектор a.

Орнамент четвёртого типа. Фрагмент отображается относительно вертикальной оси, затем осуществляется параллельный перенос получившегося рисунка.

Орнамент пятого типа. Композиция центральной симметрии и параллельного переноса.

Орнамент шестого типа. Композиция центральной симметрии, симметрии относительно вертикальной оси и параллельного переноса.

Орнамент седьмого типа. Композиция осевых симметрий относительно горизонтальной и вертикальной осей и параллельного переноса.

Глава 1.4. Виды орнаментов. Как создаются орнаменты

По-характеру композиции и расположению на украшаемой поверхности орнамент может быть нескольких видов: ленточным (его еще называют бордюром), сетчатым и розеточным.

Рассмотрим ленточные орнаменты — бордюры. Бордюром называют плоскую геометрическую фигуру, характеризующуюся векторами aи па (где n — целое число), при которых эта фигура переходит в себя, но не переходит в себя при параллельных переносах иного вида. Вектораназывают направляющим для бордюра.

Простейший бордюр построить очень просто: достаточно нарисовать какую-нибудь геометрическую фигуру и выполнить параллельный перенос на заданный вектор влево и вправо вдоль полосы. Такая «первоначальная фигура» называется фундаментальной областью бордюра.

Бордюры встречаются в разных местах: в настенных росписях, на лестничных переходах. Их можно увидеть в чугунном литье, которое используется в оградах парков, решетках мостов и набережных.

Бордюры, которые не имеют иных симметрий, кроме параллельных переносов

Бордюры, у которых фундаментальная область обладает центром симметрииО

Бордюры, у которых фундаментальная область имеет ось симметрии, параллельную вектору а

Бордюры, у которых фундаментальная область имеет ось симметрии, перпендикулярную вектору а

Бордюры, у которых фундаментальная область имеет одну ось симметрии, перпендикулярную вектору а, а другую — параллельную вектору а

Бордюры, имеющие такие оси симметрии, которых нет у фундаментальных областей

Помимо бордюров художникам-орнаменталистам известен и другой вид орнамента — сетчатый. Он заполняет всю плоскую поверхность сплошным узором. Для построения такого орнамента выделяют плоскую решетку, в которой одинаковые части повторяются в определенной геометрической последовательности. Различают пять типов плоских решеток, каждая из которых определяется двумя векторами а и b и углом п между ними. На рисунке показаны разные виды решеток: а) квадратная (а = b, а= 90°), б) прямоугольная (а = b, а= 90°), в) гексальная (а = bа = 60°), д) ромбическая (a = b, а ≠90°, а ≠60°), г) косая (a ≠b, и a≠ 90°).

Вид орнамента определяется не только структурой его решетки, но и числом элементов его симметрии. Зная геометрические закономерности, можно и самим сконструировать интересный орнамент или определить те геометрические преобразования, которые положены в его основу. Приложение 2.

Чем больше элементов симметрии содержит элементарная ячейка, тем интереснее и красивее орнамент. Каждая прямая, проходящая через сторону квадрата, а также прямая в ячейке может стать осью симметрии орнамента. Кроме того, имеется девять точек (А, В, С, D, М, О, N, L, К), вокруг которых можно повернуть ячейку, чтобы образовать новую ячейку или совместить старую ячейку саму с собой.

Помимо описанных видов орнамента в произведениях искусства встречается еще один. Такой орнамент замкнут и ограничен определенной геометрической формой (квадратом, ромбом, треугольником, кругом и др.). Орнамент, вписанный в круг или в правильный многоугольник, называется розеткой.

Глава 2. Геометрические паркеты

Паркеты из одинаковых правильных многоугольников

Сумма всех углов n-угольника равна 180°(n-2). Все углы правильного многоугольника равны; следовательно, каждый из них равен 180°(n-2)/n. В каждой вершине паркета сходится целое число углов; поэтому число 2·180° должно быть целым кратным числа 180°(n-2)/n. Преобразуем отношение этих чисел:

Разность n-2 может принимать лишь значения 1, 2 или 4; поэтому n может быть равно только 3, 4 или 6. Значит, можно получить паркеты, составленные из правильных треугольников, квадратов или правильных шестиугольников.

Паркеты из разных правильных многоугольников

Источник