Что такое основание треугольника
Основание треугольника – уравнение
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Рис. 1. Углы произвольного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
Рис. 2. Равнобедренный треугольник.
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
Рис. 3. Равносторонний треугольник.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Основание треугольника – уравнение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Рис. 1. Углы произвольного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
Рис. 2. Равнобедренный треугольник.
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
Рис. 3. Равносторонний треугольник.
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
Основание треугольника

Всего получено оценок: 97.
Всего получено оценок: 97.
Основание треугольника – это такая же сторона, как и две других. Основание редко имеет особое значение, но из-за визуальной обособленности от других сторон, ученики часто путаются и допускают ошибки. Разберем подробнее, как сторона треугольника может считаться основанием, и в каких случаях это действительно имеет значение
Стороны треугольника
У треугольника всегда три стороны. Одна из них считается основанием. Как правило, основание выделяется только построением, т.е. нижняя сторона треугольника, и приниматься за основание.
Иногда в решении указывают углы при основании произвольного треугольника. Это не совсем верно, поскольку в произвольном треугольнике все углы равнозначны, а значит не имеет смысла выделять углы при основании. Выделяются только углы при основании равнобедренного треугольника.
Нужно учитывать, что любой произвольный треугольник можно условно перевернуть, т.е. перечертить фигуру таким образом, чтобы основанием стала другая сторона. По этому разделять понятие боковых сторон и основания у произвольного треугольника не имеет смысла – это только добавит путаницы в решение задачи.
Уравнение основания треугольника, так же, как и уравнение любой из сторон треугольника, является уравнением прямой линии.
Равнобедренный треугольник
Равнобедренный треугольник – это единственный подвид треугольника, где основание имеет реальное практическое значение. Равнобедренным треугольником называется треугольник, у которого две стороны равны между собой. Равные стороны зовутся боковыми, а третья сторона считается основанием.
Существует две теоремы об основании равнобедренного треугольника. Это:
В равнобедренном треугольнике основание определяется значением сторон: равные стороны – боковые, неравная – основание.
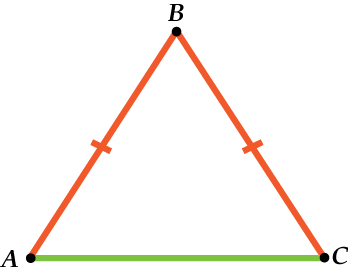
По ходу решения задачи может получится так, что основание окажется сбоку, не нужно этого пугаться. Стоит или привыкнуть к такому построению равнобедренного треугольника или каждый раз перечерчивать чертеж, разворачивая треугольник в нужную сторону.
Равносторонний треугольник
Равносторонний треугольник – это частный случай равнобедренного. У равнобедренного треугольника равны две стороны, а у равностороннего все три. Но именно из-за этого свойства значение основания равнобедренного треугольника теряется.
В равностороннем треугольнике какую сторону не выбери: две другие всегда будут равны между собой, а значит любая сторона может считаться основанием.
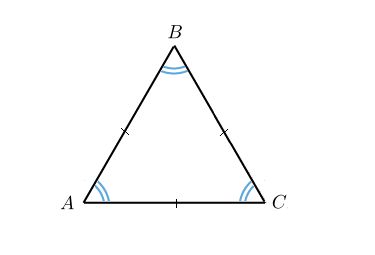
Существует формула, где часто упоминается слово основание. Это формула площади, которая равна половине произведения основания треугольника на высоту, проведенную к этому основанию. Но в качестве основания может быть принята любая сторона, главное, чтобы именно на нее падала высота. Поэтому и в этом случае выбор стороны треугольника, которую можно считать основанием, некритичен.
Что мы узнали?
Мы узнали, что такое основание треугольника. Поговорили о ситуациях, когда стоит выделять основание среди других сторон треугольника, а когда это окажется напрасной тратой времени. Обсудили значимость основания равнобедренного треугольника.
энциклопедия жизненных ответов
мы стараемся находить самые интересные вопросы и давать на них исчерпывающие ответы. заходите к нам почаще и вы всегда будете находить для себя что-нибудь новое и интересное.
темы вопросов
актуальные комментарии к ответам
Что такое основание треугольника?
Треугольник — это многоугольник с 3-мя сторонами (либо 3-мя углами). Стороны треугольника нередко обозначаются малеханькими буквами, которые соответствуют большим буквам, обозначающим обратные вершины.
Остроугольным треугольником именуется треугольник, у которого все три угла острые.
Тупоугольным треугольником именуется треугольник, у которого один из углов тупой.
Прямоугольным треугольником именуется треугольник, у которого один из углов прямой, другими словами равен 90°; стороны a, b, образующие прямой угол, именуются катетами; сторона c, обратная прямому углу, именуется гипотенузой.
Равнобедренным треугольником именуется треугольник, у которого две его стороны равны (a = c); эти равные стороны именуются боковыми, 3-я сторона именуется основанием треугольника.
Равносторонним треугольником именуется треугольник, у которого все его стороны равны (a = b = c). В том случае в треугольнике не равна ни одна из его сторон (abc), то это неравносторонний треугольник.
Главные характеристики треугольников
В любом треугольнике:
Признаки равенства треугольников
Треугольники равны, в том случае у их соответственно равны:
Признаки равенства прямоугольных треугольников
Два прямоугольных треугольника равны, в том случае производится одно из последующих критерий:
Высота треугольника — это перпендикуляр, опущенный из хоть какой вершины на обратную сторону (либо её продолжение). Эта сторона именуется основанием треугольника. Три высоты треугольника всегда пересекаются в одной точке, именуемой ортоцентром треугольника.
Ортоцентр остроугольного треугольника размещен снутри треугольника, а ортоцентр тупоугольного треугольника — снаружи; ортоцентр прямоугольного треугольника совпадает с верхушкой прямого угла.
Медиана — это отрезок, соединяющий всякую верхушку треугольника с серединой обратной стороны. Три медианы треугольника пересекаются в одной точке, всегда лежащей снутри треугольника и являющейся его центром масс. Эта точка разделяет каждую медиану в отношении 2:1, считая от вершины.
Биссектриса — это отрезок биссектрисы угла от вершины до точки скрещения с обратной стороной. Три биссектрисы треугольника пересекаются в одной точке, всегда лежащей снутри треугольника и являющейся центром вписанного круга. Биссектриса разделяет обратную сторону на части, пропорциональные прилегающим сторонам.
Срединный перпендикуляр — это перпендикуляр, проведенный из средней точки отрезка (стороны). Три срединных перпендикуляра треугольника пересекаются в одной точке, являющейся центром описанного круга.
В остроугольном треугольнике эта точка лежит снутри треугольника, в тупоугольном — снаружи, в прямоугольном — посреди гипотенузы. Ортоцентр, центр масс, центр описанного и центр вписанного круга совпадают исключительно в равностороннем треугольнике.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Подтверждение аксиомы Пифагора
Построим квадрат AKMB, используя гипотенузу AB как сторону. Потом продолжим стороны прямоугольного треугольника ABC так, чтоб получить квадрат CDEF, сторона которого равна a + b. Сейчас ясно, что площадь квадрата CDEF равна ( a + b ) 2. С иной стороны, эта площадь равна сумме площадей четырёх прямоугольных треугольников и квадрата AKMB, другими словами,
c 2 + 4 (ab / 2) = c 2 + 2 ab,
Соотношение сторон в случайном треугольнике
В общем случае (для случайного треугольника) имеем:
c 2 = a 2 + b 2 — 2 ab * cos C,
где С — угол меж сторонами а и b.
Дополнительно на New-Best.com:
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
Добавить комментарий Отменить ответ
Для отправки комментария вам необходимо авторизоваться.
Равнобедренный тупоугольный треугольник – основание, формула
Равнобедренный треугольник наиболее часто встречается в задачах по геометрии. Так сложилось, что равнобедренный треугольник не столь прост в решении, как правильный, но при этом обладает рядом интересных свойств, которые могут затруднить решение задачи.
Равнобедренный треугольник
Равнобедренным треугольником зовется треугольник, две стороны которого равны между собой. Тогда третья сторона зовется основанием, а равные стороны считаются боковыми.
Рис. 1. Равнобедренный треугольник.
Любой равнобедренный треугольник имеет ряд свойств:
Именно эти два свойства определяют специфические особенности равнобедренных треугольников. Как и произвольные треугольник, равнобедренные треугольники бывают 3 видов:
Углы при основании равнобедренного треугольника равны, а сумма углов треугольника всегда равна 180 градусам. Поэтому в равнобедренном и тупоугольном треугольнике наибольший угол всегда лежит напротив основания. Если такой угол лежал бы при основании, то сумма углов превысила бы 180 градусов, а это невозможно.
Тупоугольный треугольник
Тупой угол это угол больше 90 градусов. Очень часто тупоугольный треугольник стараются изобразить так, чтобы тупой угол находился у основания треугольника. Такой подход облегчает восприятие фигуры.
Рис. 2. Тупоугольный треугольник.
В любой треугольник тупой угол добавляет несколько особенностей:
Равнобедренный тупоугольный треугольник
Равнобедренный треугольник это треугольник, который с одной стороны содержит в себе тупой угол, с другой имеет две равные между собой стороны.
Такой равнобедренный треугольник сложно воспринимать визуально. Дело в том, что с одной стороны тупоугольные треугольники ученики часто изображают так, чтобы тупой угол был при основании.
Но если тупой угол начертить в основании, то реальное основание тупоугольного равнобедренного треугольника будет визуально совпадать с боковой стороной. Такой подход очень часто приводит к ошибкам. Поэтому равнобедренный тупоугольный треугольник лучше рисовать с тупым углом напротив основания, а сам угол подписывать прямо на чертеже.
Рис. 3. Равнобедренный тупоугольный треугольник.
С другой стороны, этот подход не всегда помогает воспринимать фигуру именно как тупоугольный треугольник. Поэтому и нужно подписывать углы, а при решении доказывать или проверять условие на наличие доказательств существования тупого угла в треугольнике.
Что мы узнали?
Мы узнали, что такое тупоугольный равнобедренный треугольник и какими особенностями он обладает. Поговорили о том, как лучше начертить тупоугольный треугольник и выделили проблемы, которые могут возникнуть с этим вопросом при решении задач.















