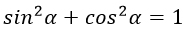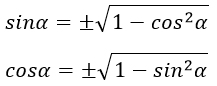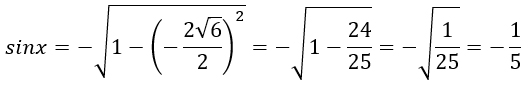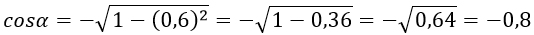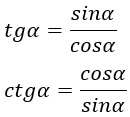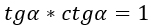Что такое основное тригонометрическое тождество
Основные тригонометрические тождества
Тригонометрические тождества — это равенства, которые устанавливают связь между синусом, косинусом, тангенсом и котангенсом одного угла, которая позволяет находить любую из данных функций при условии, что будет известна какая-либо другая.
\sin^<2>\alpha + \cos^ <2>\alpha = 1
tg \alpha \cdot ctg \alpha = 1
Содержание
Зависимость между синусом и косинусом
\sin^ <2>\alpha+\cos^ <2>\alpha=1
Данное тождество говорит о том, что сумма квадрата синуса одного угла и квадрата косинуса одного угла равна единице, что на практике дает возможность вычислить синус одного угла, когда известен его косинус и наоборот.
При преобразовании тригонометрических выражений очень часто используют данное тождество, которое позволяет заменять единицей сумму квадратов косинуса и синуса одного угла и также производить операцию замены в обратном порядке.
Нахождение тангенса и котангенса через синус и косинус
Данные тождества образуются из определений синуса, косинуса, тангенса и котангенса. Ведь если разобраться, то по определению ординатой y является синус, а абсциссой x — косинус. Тогда тангенс будет равен отношению \frac
Зависимость между тангенсом и котангенсом
tg \alpha \cdot ctg \alpha=1
Зависимости между тангенсом и косинусом, котангенсом и синусом
Примеры с решениями задач на использование тригонометрических тождеств
Пример 1
Решение
\sin^<2>\alpha + \left (-\frac12 \right )^2 = 1
Это уравнение имеет 2 решения:
\sin \alpha = \pm \sqrt <1-\frac14>= \pm \frac <\sqrt 3>
По условию \frac<\pi> <2>. Во второй четверти синус положителен, поэтому \sin \alpha = \frac<\sqrt 3> <2>.
tg \alpha = \frac<\sqrt 3> <2>: \frac12 = \sqrt 3
Пример 2
Решение
Алгебра
Лучшие условия по продуктам Тинькофф по этой ссылке
Дарим 500 ₽ на баланс сим-карты и 1000 ₽ при сохранении номера
. 500 руб. на счет при заказе сим-карты по этой ссылке
Лучшие условия по продуктам
ТИНЬКОФФ по данной ссылке
План урока:
Основное тригонометрическое тождество
Несложно догадаться, что синус и косинус угла – это величины, связанные друг с другом. Отложим на единичной окружности произвольный угол α и опустим из точки А перпендикуляр на ось Ох, в некоторую точку В:
Изучим треугольник АОВ. Он прямоугольный, а потому для него можно записать теорему Пифагора:
Мы рассматриваем единичную окружность, а потому ОА = 1, ОВ = соsα, AB = sinα. Подставив эти величины в равенство, получим тождество:
sin 2 α + соs 2 α = 1
Его называют основным тригонометрическим тождеством, ведь именно оно связывает значение двух прямых тригонометрических ф-ций – синуса и косинуса.
Задание. В прямоугольном треугольнике есть угол α. Известно, что sin α = 0,8. Чему равен соsα?
Решение. Подставим в основное тригон-кое тождество значение sinα = 0,8 и получим уравнение:
sin 2 α + соs 2 α = 1
соsα = – 0,6 или соsα = 0,6
Нашли два возможных значения косинуса. Но по условию α – это острый угол, ведь в прямоугольном треугольнике угол не может быть больше 90°. То есть угол α относится к первой четверти, а потому его косинус положителен. Значит, соsα = 0,6.
Рассмотренный пример показал, что одному заданному значению синуса соответствует сразу два противоположных друг другу значения косинуса. Верно и обратное. Действительно, отложим по оси Ох некоторую величину соsα и проведем вертикальную линию, чтобы найти соответствующие ему значения синуса. Она пересечет единичную окружность в двух точках с противоположными ординатами:
По этой причине при решении задач на использование основного тригон-кого тождества обычно указывают, к какой четверти относится угол α.
Задание. Вычислите sinα, если соsα = 0,28 и α принадлежит IV четверти.
sin 2 α + соs 2 α = 1
sin α = –0,96 или sin α = 0,96
Так как α принадлежит IV четверти, то sinα должен быть отрицательным, поэтому sinα = – 0,96.Напомним, что в IV четверти значение косинуса положительно, ведь соответствующая ей дуга единичной окружности располагается правее оси Оу, то есть абсциссы точек, принадлежащих ей, положительны.
Задание. Найдите tgα, если sinα = 5/13 и π/2 2 α + соs 2 α = 1
соs 2 α = 1 – sin 2 α = 1 – (5/13) 2 = 169/169 – 25/169 = 144/169
соsα = – 12/13 или соsα = 12/13
Условие π/2 2 α + соs 2 α = 1
Далее поделим его на величину соs 2 α:
Крайнее левое слагаемое – это величина tg 2 α, а следующая дробь равна единице, так как у неё совпадают числитель и знаменатель:
В итоге нам удалось получить ф-лу, которая связывает значение тангенса и косинуса угла. Есть такая формула и для котангенса. Для ее получения необходимо поделить основное тригон-кое тождество на sin 2 α:
Задание. Известно, что tgα = 0,75. Найдите соsα и sinα, если угол α принадлежит III четверти.
Просто подставляем в ф-лу известное значение тангенса и решаем получившееся уравнение. Для простоты вычислении заменим десятичную дробь 0,75 на обычную 3/4:
Так как угол относится к III четверти, где косинус отрицателен, то
Синус угла найдем, используя основное тригон-кое тождество:
sin 2 α + соs 2 α = 1
sin 2 α = 1 – соs 2 α = 1 – (– 0,8) 2 = 1 – 0,64 = 0,36
sinα = – 0,6 или sinα = 0,6
С учетом того, что в III четверти синус становится отрицательным, следует выбрать вариант sinα = – 0,6
Ответ: sinα = – 0,6; соsα = – 0,8.
Иногда ф-лы используют не для вычисления значений тригон-ких выражений, а для упрощения выражений. Из тождества sin 2 α + соs 2 α = 1 несложно получить из выражения
sin 2 α = 1 – соs 2 α
соs 2 α = 1 – sin 2 α
которые помогают в работе с длинными ф-лами.
Задание. Упростите выражение
4sin 2 α + 9соs 2 α – 6
таким образом, чтобы в нем не содержалось синуса.
Решение. Произведем замену sin 2 α = 1 – соs 2 α:
4sin 2 α+ 9соs 2 α – 6 = 4(1 – соs 2 α)+ 9соs 2 α – 6 =
= 4 – 4 соs 2 α + 9соs 2 α – 6 = 5соs 2 α – 2
Видим, что получилось значительно более простое выражение.
Задание. Избавьтесь от синуса в выражении
sin 4 α – соs 4 α
Решение. Воспользуемся ф-лой разности квадратов:
sin 4 α – соs 4 α = (sin 2 α – соs 2 α)(sin 2 α + соs 2 α) = (sin 2 α – соs 2 α)•1 =
= 1 – соs 2 α– соs 2 α = 1 – 2 соs 2 α
Задание. Упростите дробь
Тригонометрические функции суммы и разности
Легко проводить вычисления, когда все тригонометрические действия выполняются над одним углом α. Однако иногда в задачах добавляется ещё один угол, который обычно обозначают как β. Существуют ф-лы, с помощью которых можно вычислять тригон-кие ф-ции от суммы и разности углов α и β.
Вывод этих ф-л достаточно сложен, поэтому сначала мы просто без доказательства приведем две из них, позволяющие вычислять синус суммы и косинус суммы:
Достаточно запомнить их, а далее следующие формулы можно выводить из них. Так, если вместо β подставить угол (–β), то получим формулы для разности. При этом мы используем тот факт, что синус – нечетная ф-ция, то естьsin (– β) = – sinβ, а косинус – четная ф-ция, то есть соs (– β) = соsβ:
Теперь поступим также с ф-лой для косинуса разности:
Итак, нам удалось получить ф-лы для нахождения синуса и косинуса суммы и разности углов.
С помощью этих формул возможно вычислить значение тригон-ких ф-ций для некоторых нестандартных углов. (Стандартными считаются углы в 0°, 30°, 45°, 60° и 90°, ведь для них значение тригон-ких ф-ций можно узнать из таблички.)
Задание. Вычислите соs 150°.
Решение. В табличке стандартных углов есть углы, равные 90° и 60°. Их сумма как раз равна 150°. Поэтому запишем:
Задание. Вычислите синус, косинус и тангенс для угла 15°.
Решение. Угол в 15° можно представить как разность 45° – 30°. Тогда синус будет вычисляться так:
Далее вычислим косинус:
Можно выполнить проверку. Полученные значения должны удовлетворять основному тригон-кому тождеству. И действительно:
Проверка пройдена: сумма квадратов синуса и косинуса оказалась равной единице. Теперь посчитаем tg 15°, используя определение тангенса:
Задание. Вычислите значение тригонометрического выражения
sinπ/7 соsπ/42 + sinπ/42 соsπ/7
Решение: Значение тригон-ких ф-ций для углов π/7 и π/42 мы не знаем, однако это не помешает вычислениям. Можно заметить, что исходное выражение представляет собой синус суммы π/7 и π/42:
sinπ/7 соsπ/42 + sinπ/42 соsπ/7 = sin (π/7 + π/42) = sinπ/6 = 1/2
Задание. Упростите выражение
Вынесем за скобки множитель 2:
Теперь произведем замену:
C учетом этого можно переписать выражение и использовать ф-лу суммы косинусов:
Формулы двойного угла
Что будет, если формулу синуса суммы подставить не два различных угла α и β, а два одинаковых угла α и α? Получится ф-ла для синуса двойного угла:
Аналогично можно составить ф-лу и для косинуса двойного угла:
Итак, справедливы следующие ф-лы:
Задание. Вычислите sin 120° и соs 120°.
Задание. Упростите выражение
соs 2 t – соs 2t = соs 2 t – (соs 2 t – sin 2 t) = соs 2 t – соs 2 t + sin 2 t = sin 2 t
Задание. Докажите, что функция
является периодической и имеет период, равный π.
Решение. Используем ф-лу квадрата суммы:
Таким образом, исходную ф-цию можно переписать в виде
По определению, ф-ция является периодической с периодом Т, если выполняется условие у(х + Т) = у(х). Поэтому подставим в нашу ф-цию величину х + π:
Получили, что у(х + π) = y(x), то есть ф-ция имеет период, равный π.
Задание. Выведите формулы синуса и косинуса тройного угла.
Решение. Для их получения следует использовать ф-лу синуса суммы углов, в которую подставляют вместо β величину 2α:
Аналогично можно получить и ф-лу для косинуса тройного угла:
Формулы понижения степени
Если нам необходимо узнать косинус угла, который вдвое больше табличного, мы используем ф-лу:
соs 2α = соs 2 α – sin 2 α
А что делать, если нам надо вычислить косинус угла, который вдвое меньше известного? Попробуем преобразовать ф-лу косинуса двойного угла:
В результате нам удалось получить тождество, позволяющее по косинусу удвоенного угла найти косинус самого угла! Однако значительно чаще в тригонометрии это равенство записывают в обратном порядке:
и называют ф-лой понижения степени. Действительно, в левой части стоит косинус в квадрате, а справа – косинус без квадрата, но вычисляется он от угла 2α, а не α.
Попробуем получить аналогичную ф-лу и для синуса. Для этого используем основное тригон-кое тождество:
С помощью этих ф-л можно вычислять тригон-кие ф-ции для некоторых малых углов. Так, ранее мы с использованием ф-лу разности синусов определили, что
При этом мы представляли угол 15° как разность 45° – 30°. Но как посчитать соs 7,5°? Этот угол невозможно представить как разницу или сумму известных нам табличных углов (0°, 30°; 45°; 60° и 90°). Однако поможет ф-ла понижения степени. Действительно, ведь 2•7,5° = 15°. Тогда можно записать:
Мы нашли соs 2 7,5°. Чтобы узнать соs 7,5°, необходимо извлечь квадратный корень:
Так как угол 7,5° принадлежит I четверти, то его косинус должен быть положительным, поэтому можно записать:
Видно, что получается довольно громоздкое выражение. Используя ф-лу понижения степени, можно найти косинус и угла, который ещё вдвое меньше, то есть равен 3,75°, но в результате получится ещё более громоздкое выражение.
Задание. Вычислите sinπ/8.
Решение. Угол π/4 является табличным (его градусная мера составляет 45°). Поэтому можно записать:
Эти примеры показывают, что тригон-кие ф-ции многих нестандартных углов можно выразить, используя квадратные корни. Возникает вопрос – а любую ли тригонометрическую ф-цию можно выразить таким способом? Оказывается, что нет. Например, sin 10° невозможно найти ни в одной, даже самой подробной тригонометрической таблице. Мы не будем это доказывать, но эту величину невозможно представить в виде выражения, используя арифметические операции и корни. Однако существуют приближенные методы, позволяющие с любой наперед заданной точностью вычислять значение тригонометрических ф-ций.
Формулы приведения
Возможно, вы уже заметили, что синусы и косинусы принимают одинаковые значения в углах, чья сумма равна 90°. Например, sin30° = соs60° = 1/2, и при этом 30° + 60° = 90°. Также мы знаем, что sin 45° = соs 45° (45° + 45° = 90°) и sin60° = соs30° (60° + 30°). В чем причина такой закономерности и справедлива ли она для нестандартных углов?
Используя ф-лу синуса разности, мы можем записать, что
Полученная ф-ла sin (90° – α) = соsα называется формулой приведения. При ее выводе мы использовали тот факт, что sin 90° = 1, а соs 90° = 0, поэтому формула получилась очень простой. Однако синусы и косинусы других углов, кратных 90° (или кратных π/2, если измерять углы в радианах), также равны 0, 1 или – 1, поэтому для них тоже можно получить подобные простые ф-лы, например:
Похожих ф-л можно написать несколько десятков! Все их запоминать не надо, так как существует особое мнемоническое правило, позволяющее записать необходимую ф-лу.
Пусть есть некоторое тригон-кое выражение вида
где f – тригонометрическая ф-ция (sin; соs; tg; ctg)
k– угол, кратный π/2 (π/2, π, 3π/2, 2π)
Мы хотим заменить ее другой ф-цией, только от угла α. На первом шаге мы смотрим на слагаемое k. Если оно кратно π (– π, π, 2π), то ф-ция f остается неизменной. Если же слагаемое k – это число π/2 или 3π/2, то ф-цию f надо поменять на так называемую кофункцию (синус меняем на косинус, тангенс на котангенс и наоборот).
Далее надо определить знак, стоящий перед новой ф-цией. Для этого мы предполагаем, что α – это острый угол, то есть он принадлежит I четверти. Далее с учетом этого предположения смотрим, в какую четверть попадает угол k ± α, и какое значение принимает там исходная тригонометрическая ф-ция. Если она отрицательна, то перед новой тригонометрической ф-цией надо поставить минус. В противном случае ничего ставить не надо.
Лучше всего изучить это алгоритм на примерах.
Задание. Упростите выражение соs (π/2 + α).
Решение. Первый шаг – смотрим на слагаемое под знаком косинуса. Это число π/2. Оно НЕ кратно π, а потому мы должны поменять косинус на синус:
Второй шаг – надо определить, надо ли ставить минус перед синусом. Если α – это острый угол, то угол (π/2 + α) попадет во II четверть:
Во второй четверти косинус отрицателен, а потому перед синусом следует поставить минус:
Важное примечание. В этом примере для составления формулы приведения мы «предположили», что угол α является острым. В результате нам удалось получить формулу соs (π/2 + α) = – sinα. Однако отметим, что полученная нами формула выполняется для абсолютно любых значений угла α, а не только для 0° 1 2 + 3 соs2x
Основное тригонометрическое тождество
Классическое основное тригонометрическое тождество.
Перед тем, как переходить к различным тригонометрическим ужасам, в школе разбирают основное тригонометрическое тождество, благодаря которому, можно находить синус угла, зная его косинус, и наоборот.
Само тождество выглядит весьма мило:
Из этой формулы выразим синус и косинус:
Стоит обратить особое внимание на знаки «±». Почему их важно не забыть?
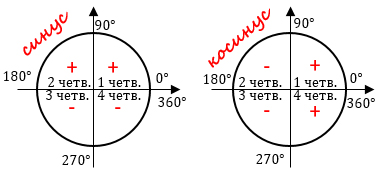
Посмотри на картинку ниже.
Если угол находится в первой четверти, то знаки его синуса и косинуса положительны.
Если угол находится во второй четверти, то знак его синуса положительный, а знак косинуса отрицательный.
Если угол находится в третьей четверти, то знаки его синуса и косинуса отрицательны.
Если угол находится в четвертой четверти, то знак его синуса отрицательный, а знак косинуса положительный.
Давай попробуем решить парочку примеров.
Найдите sinx, если cosx = 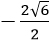
Угол х находится в третьей четверти, значит синус этого угла будет отрицательный и при выражении синуса из основного тригонометрического тождества мы должны перед корнем поставить знак минус.
Переводим дробь в десятичную.
Найдите cosx, если sinx = 0.6 и 90° < x < 180°.
Определяем знак косинуса. Угол х находится во второй четверти, значит значение косинуса будет отрицательным (см. окружности выше).
Другие полезные тождества.
Еще нельзя не упомянуть другие тригонометрические тождества, которые в своей сущности также являются основными.
2. Связь между тангенсом и котангенсом.
3. Следствия из основного тригонометрического тождества.
Эти формулы получаются путем деления обеих частей равенства на косинус (первая формула) и на синус (вторая формула).
Основные тригонометрические формулы и тождества sin, cos, tg, ctg
Основные тождества тригонометрии
Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.
Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).
Формулы приведения
Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.
Формулы приведения являются следствием периодичности тригонометрических функций.
Тригонометрические формулы сложения
Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.
Тригонометрические формулы сложения
На основе формул сложения выводятся тригонометрические формулы кратного угла.
Формулы кратного угла: двойного, тройного и т.д.
Формулы половинного угла
Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.
Формулы половинного угла
Формулы понижения степени
Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:
Общий вид формул понижения степени
Сумма и разность тригонометрических функций
Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.
Сумма и разность тригонометрических функций
Произведение тригонометрических функций
Формулы произведения тригонометрических функций
Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка
1.2.4 Основные тригонометрические тождества
Видеоурок: Тригонометрические тождества
Лекция: Основные тригонометрические тождества
Итак, напомним, что при рассмотрении тригонометрических функций, мы используем единичную окружность, с радиусом, равным единице.
Рассмотрим произвольный прямоугольный треугольник, полученный в результате движения радиус-вектора на некоторый угол.
К прямоугольному треугольнику применима теорема Пифагора, в соответствии с которой квадрат гипотенузы будет равен сумме квадратов остальных сторон треугольника. Так как мы знаем, что синусу соответствует значение ординаты на плоскости, то есть величина противолежащего катета, а косинусу значение абсциссы (прилежащего катета). Так же нам известно, что гипотенуза треугольника является радиусом окружности, длина которого равна единицы, то теорему Пифагора можем получить в следующем виде:
Остальные тригонометрические тождества мы можем получить, зная определение тангенса и котангенса.
Давайте перемножим первое и второе уравнение и посмотрим, что получилось. В результате данного математического действия получим, что произведение тангенса на котангенс равно единице:
А теперь давайте возьмем первое основное тождество и почленно разделим все на cos 2 α или на sin 2 α. В результате этого получим:
Первое тождество справедливо для всех углов. Остальные же используются исключительно при углах, синус и косинус которых не равен 0.