Что такое основные физические величины
Виды физических величин и их единицы измерения
Физические величины — что под этим понимается
Физические величины — это понятие в физике описывает характеристики тел или процессов, которые могут быть измерены на опыте с использованием измерительных методов и приборов.
Физическая величина — это одно из свойств материальных объектов (физической системы, явления или процесса), общее в качественном отношении для многих физических объектов, но по количественной характеристике индивидуальное для каждого из них.
Значение физической величины выражается одним или несколькими числами, характеризующими необходимую физическую величину, у которой обязательно должна быть указана размерность.
Размер физической величины — это значения чисел, указанные в значении физической величины.
Описание основных физических величин в системе СИ, единицы их измерения, обозначения и формулы
Основными физическими величинами в Международной системе единиц (СИ) являются: длина, масса, время, сила электрического тока, термодинамическая температура, количество вещества, сила света.
Единицы измерения основных физических величин в системе СИ
Время в системе СИ измеряется в секундах (с).
Расчет величины секунды основан на фиксировании численного значения частоты сверхтонкого расщепления основного состояния атома цезия-133 при температуре 0 °К, равной в точности 9 192 631 770 Гц.
Солнечные сутки разбираются на 24 часа, каждый час разбирается на 60 минут, а каждая минута состоит из 60 секунд. Таким образом, секунда — это 1 / ( 24 * 60 * 60 ) = 1 / 86400 от солнечных суток.
Единица длины по системе СИ — это метр (м). Величина метра определяется фиксацией численного значения скорости света в вакууме, равной 299 792 458 м/с.
Единицей измерения термодинамической температуры является Кельвин (K). В 1967-2019 годах Кельвин определялся как 1/273,16 части термодинамической температуры тройной точки воды. Шкала Кельвина использует тот же шаг, что и шкала Цельсия. 0 °K — это температура абсолютного нуля, а не температура плавления льда. Согласно современному определению что такое Кельвин, 0 °C установлены таким образом, что температура тройной точки воды на фазовой диаграмме равна 0,01 °C. В итоге шкалы Цельсия и Кельвина сдвинуты на 273,15 °.
| Основная физическая величина | Обозначение | Единица измерения в системе СИ |
| Длина | l | метр (м) |
| Масса | m | килограмм (кг) |
| Время | t | секунда (с) |
| Сила электрического тока | I | Ампер (А) |
| Термодинамическая температура | T | Кельвин (К) |
| Количество вещества | n | моль |
| Сила света | I_c | Кандела (кд) |
Табл.1. Основные физические величины, их обозначения и единицы измерения.
Производные единицы СИ, имеющие собственные наименования
Производные единицы СИ — это единицы измерения, которые исходят от семи основных единиц, определенных Международной системой единиц (СИ).
Такие единицы либо безразмерные, либо могут быть выражены с помощью различных математических операций из основных единиц СИ.
Пространство и время
Единиц измерения, входящих в систему СИ и имеющих собственные названия, которые относятся к пространству и времени — нет.
Периодические явления, колебания и волны, акустика
Частота — это число колебаний совершаемых за одну секунду. Единица измерения названа в честь физика Генриха Герца и обозначается Гц.
Тепловые явления
Энергия — это физическая величина, показывающая какую работу может совершить тело. Измеряется в джоулях (Дж).
Механика
Плоский угол — это часть плоскости, ограниченная двумя лучами, выходящими из одной точки. В системе СИ измеряется в радианах (рад).
Телесный угол — часть пространства, ограниченная некоторой конической поверхностью. Измеряется в системе СИ в стерадианах (ср).
Молекулярная физика
Давление — это скалярная физическая величина равная отношению силы давления, приложенной к данной поверхности, к площади этой поверхности. Единицей измерения в системе СИ является паскаль (Па).
Активность катализатора — характеристика, показывающая насколько катализатор активен в процессе своей работы.
Электричество и магнетизм
Сила — физическая величина, которая характеризует действие на тело других тел, в результате чего у тела изменяется скорость или оно деформируется. Измеряется в ньютонах (Н).
Мощность — это физическая величина, равная отношению работы к промежутку времени, за который совершенна эта работа. В Международной системе (СИ) единицей измерения мощности является ватт (Вт).
Электрический заряд — это физическая величина, характеризующая свойство тел или частиц входить в электромагнитные взаимодействия и определяющая значение сил и энергий этих взаимодействий. Единица измерения в системе СИ — это кулон (Кл).
Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к величине этого заряда. Измеряется в вольтах (В).
Сопротивление — физическая величина, характеризующая способность проводника препятствовать прохождению тока. Единица измерения — Ом. Источник электрической энергии является проводником и всегда имеет некоторое сопротивление, поэтому ток выделяет в нем тепло. Такое сопротивление называется внутренним. Если оно очень мало, то ток короткого замыкания будет большим, что может вывести источник тока из строя.
Емкость — это физическая величина, которая характеризует способность накапливать электрический заряд на одной из металлических обкладок конденсатора, равная отношению заряда к напряжению и измеряется в фарадах (Ф).
Конденсатор — это совокупность двух проводников, находящихся на малом расстоянии друг от друга и разделенных слоем диэлектрика. На значение емкости влияют геометрические размеры и среда. Материал, из которого сделаны обкладки конденсатора, может быть разным.
Электрическая проводимость (электропроводность) — это способность веществ пропускать электрический ток под действием электрического напряжения. Электрическая проводимость — величина, обратная сопротивлению. Измеряется в сименсах (См).
Характер электропроводности может быть разный, поэтому вещества делятся на электролиты (вещества, растворы и расплавы, проводящие электрический ток) и неэлектролиты (вещества, растворы и расплавы, которые не проводят электрический ток).
Оптика, электромагнитное излучение
Световой поток — величина, измеряемая количеством энергии, которую излучает источник света за единицу времени. В системе СИ единицей измерения светового потока является люмен (лм).
Освещенность — это величина светового потока, приходящаяся на единицу площади освещаемой поверхности. Освещенность измеряется в люксах.
Магнитный поток — физическая величина, численно равная произведению модуля магнитной индукции на площадь контура и на косинус угла между нормалью к контуру и вектором магнитной индукции. Единицей измерения магнитного потока в системе СИ является вебер (Вб).
Магнитная индукция — это векторная физическая величина, модуль которой численно равен максимальной силе, действующей со стороны магнитного поля на единичный элемент тока. Единичный элемент тока — это проводник длиной 1 м и силой тока в нем 1 А. Единицей измерения магнитной индукции в системе СИ является тесла (Тл).
Индуктивность — это физическая величина, характеризующая способность проводника с током создавать магнитное поле. Единица измерения — генри (Гн).
Радиоактивность — это способность некоторых атомных ядер самопроизвольно превращаться в другие ядра с испусканием различных видов радиоактивных излучений и элементарных частиц. Различают радиоактивность естественную – для существующих в природе неустойчивых изотопов, а также искусственную — для изотопов, полученных с использованием ядерных реакций. Единицей измерения радиоактивности является беккерель (Бк).
Поглощенная доза ионизирующего излучения — величина энергии ионизирующего излучения, переданная веществу. В единицах СИ поглощенная доза измеряется в джоулях, деленных на килограмм, и имеет специальное название — грей (Гр).
Эффективная доза ионизирующего излучения — величина, используемая как мера риска возникновения отдаленных последствий облучения всего человека и отдельных его органов и тканей с учетом их радиочувствительности. Единицей эквивалентной дозы является зиверт (Зв).
Собственные наименования имеют 22 производные единицы измерения, которые представлены в таблице 2.
| Величина | Единица измерения | Обозначение |
| Частота | герц | Гц |
| Температура по шкале Цельсия | градус Цельсия | <>^оС |
| Энергия | джоуль | Дж |
| Плоский угол | радиан | рад |
| Телесный угол | стерадиан | ср |
| Давление | паскаль | Па |
| Активность катализатора | катал | кат |
| Сила | ньютон | Н |
| Мощность | ватт | Вт |
| Электрический заряд | кулон | Кл |
| Разность потенциалов | вольт | В |
| Сопротивление | ом | Ом |
| Ёмкость | фарад | Ф |
| Магнитный поток | вебер | Вб |
| Магнитная индукция | тесла | Тл |
| Индуктивность | генри | Гн |
| Электрическая проводимость | сименс | См |
| Световой поток | люмен | лм |
| Освещенность | люкс | лк |
| Радиоактивность | беккерель | Бк |
| Поглощенная доза ионизирующего излучения | грэй | Гр |
| Эффективная доза ионизирующего излучения | зиверт | Зв |
Таблица 2. Таблица с произвольными единицами измерения в системе СИ, которые имеют собственные названия.
Преобразование единиц измерения
Рассмотрим в этом пункте только способы преобразования основных единиц измерения в системе СИ, а именно длины (м), массы (кг), времени (с), силы электрического тока (А), термодинамической температуры (К), количества вещества (моль).
Длина:
1 м = 0,001 км = 10 дм =100 см = 1000 мм
1 кг = 0,001 т = 0,01 ц = 1000 г = 1000000 мг
Основные физические величины
И.Ш. Коган
Излагаются две противоположные точки зрения на порядок выбора основных физических величин. Анализируется суть противоречия и показывается, что оно исчезает, если раздельно решать две разные проблемы — систематизацию физических величин и унификацию их единиц измерений. Предлагаются два различных определения для основной физической величины и для единицы основной физической величины. Указывается на то, что базирование на уровневом строении материи позволяет выявить основные физические величины с целью систематизации величин, а не принимать физические величины в качестве основных условно с целью унификации их единиц.
Оживленная дискуссия по поводу того, как выбрать основные физические величины, ведется с начала XX века. Эта дискуссия обычно предваряется различными взглядами выдающихся физиков М. Планка и А. Зоммерфельда на вопрос, суть которого можно выразить очень коротко: «Выбор основных физических величин произволен или продиктован природой?».
Точка зрения М. Планка, которую разделяет известный метролог Л. Сена [1], заключается в том, что выбор основных физических величин определяется практическими соображениями удобства пользования системой единиц физических величин. То же самое говорится и в метрологическом справочнике [2]: «Выбор физических величин, принимаемых за основные, и их число в принципе произвольны, но практические соображения приводят к некоторому ограничению свободы в выборе основных величин».
Точка зрения А. Зоммерфельда [3] иная: «Мы не придерживаемся точки зрения Планка, согласно которой вопрос о действительной размерности физической величины лишен смысла». Еще более четко сказано в работе [4]: «Мы вольны произвольно выбирать лишь единицы измерений, но размерности физических величин мы должны найти, они заданы самой природой этих величин». Такая точка зрения приводит к выводу: выбор основных физических величин должен быть продиктован природой и ни от каких систем единиц зависеть он не должен.
Попробуем иначе сформулировать выделенный выше жирным шрифтом вопрос, добавив в него всего четыре подчеркнутых слова: «Выбор основных физических величин для составления систем единиц произволен или продиктован природой?». И тогда ответ становится очевидным: практические соображения действительно приводят к ограничению свободы выбора основных единиц физических величин и к ограничению свободы выбора их числа. Но, повторяем, только для составления систем единиц измерений.
Заметим попутно, что в системах единиц не соблюдается принцип последовательности (очередности) образования единиц. Да и нужен ли он в системах единиц? Авторы работы [5] пишут: «Условия когерентности и последовательности образования производных единиц не являются совершенно жесткими и оставляют некоторую свободу как в выборе определяющих уравнений, так и в очередности образования производных единиц».
Другое дело, если речь идет не об унификации единиц физических величин, а о систематизации самих физических величин. Если вопросы измерений при этом не затрагиваются вообще. В этом случае правильной оказывается точка зрения А. Зоммерфельда. Ведь природе безразлично, какие системы единиц удобны человеку на планете Земля. И никакие практические соображения в этом случае не могут влиять на то, каким должен быть состав основных физических величин.
Последние несколько веков именно унификация единиц определяла, какими должны быть те основные физические величины, единицы которых положены в основу систем единиц. Унификация единиц и сейчас продолжает диктовать решение этой проблемы и будет стремиться диктовать всегда. Об этом как раз и свидетельствуют поправки к определению размерности в монографии Л. Брянского [6], когда слова «в системе величин»заменяются словами «в системе единиц».
Однако исследования по проблеме систематизации физических величин показывают: после того, как систематизация физических величин начинает проводиться без оглядки на системы единиц, начинает выясняться, что некоторые основные физические величины, единицы которых положены в основу СИ, не способствуют такой систематизации. Об этом свидетельствует аналитический обзор [7] истории развития проблемы систематизации физических величин.
Оказывается, некоторые часто применяемые единицы СИ необходимо корректировать с учетом выводов, вытекающих из процесса систематизации физических величин. Естественно, что после такой коррекции пришлось бы вносить соответствующие изменения в метрологические стандарты и в учебные пособия. К сожалению, подобная необходимость коррекции единиц СИ обречена на активное противодействие метрологов-практиков.
3. КАКИМИ ДОЛЖНЫ БЫТЬ ОСНОВНЫЕ ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ?
Для основной физической величины имеется стандартное определение [2]. Это «физическая величина, входящая в систему величин и условно принятая в качестве не зависящей от других величин этой системы». Нами предлагается дифференцировать это определение.
Развивающаяся сейчас уровневая физика тоже «не понимает» равноправия физических величин. Системный подход, одна из основ уровневой физики, требует придерживаться принципа причинности, следствием которого является принцип последовательности. Содержание принципа последовательности таково: то, что находится на более низком иерархическом уровне, должно определяться тем, что находится на более высоком иерархическом уровне.
ТЕМА 2. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ И ИХ ЕДИНИЦЫ
Физические величины
Физические величины разделяют:
1) основные – физические величины, входящие в систему величин и условно принятые в качестве независимых от других величин этой системы (пример – масса m);
2) производные – физические величины, входящие в систему величин и определяемые через основные величины этой системы (пример – сила F = m·a).
К основным величинам относятся: длина, масса, время, сила электрического тока, термодинамическая температура, количество вещества, сила света. К производным – такие, как сила, частота ит.д.
Единицы физических величин. Система единиц СИ
Единица измерения физической величины – физическая величина фиксированного размера, которой условно присвоено числовое значение, равное 1, и применяемая для количественного выражения однородных с ней физических величин.
Совокупность основных и производных единиц физических величин, образованная в соответствии с принципами для заданной системы физических величин называется системой единиц физических величин.
Единица физической величины, входящая в принятую систему единиц, называется системной.
В РФ используется международная система единиц СИ, устанавливаемая ГОСТ 8.417 – 2002 «ГСИ. Единицы величин».
Единицы, входящие в систему, делятся на основные (единица основной физической величины в данной системе) и производные (единица производной физической величины системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами или с основными и уже определенными производными).
Таблица 2.1 – Основные единицы системы СИ
| Величина | Единица | ||
| наименование | рекомендуе-мое обозна-чение | наименование | обозначение |
| Длина | l | метр | м |
| Масса | m | килограмм | кг |
| Время | t | секунда | с |
| Сила электрического тока | I | ампер | А |
| Термодинамическая температура | T | кельвин | К |
| Количество вещества | n, ν | моль | моль |
| Сила света | J | кандела | кд |
Таблица 2.2 – Пример производных единиц системы СИ
ГОСТ 8.417 устанавливает разрешенные к применению наравне с единицами СИ единицы других систем и внесистемные единицы – единица физической величины, не входящая в принятую систему единиц (таблица 2.3).
Таблица 2.3 – Пример внесистемных единиц, допускаемых к применению наравне с единицами системы СИ
Также стандарт устанавливает кратные (единица физической величины, в целое число раз большая системной и внесистемной единицы) и дольные(единица физической величины, в целое число раз меньшая системной или внесистемной единицы) (таблица 2.4).
Таблица 2.4 – Множители и приставки, используемые для образования наименований и обозначений десятичных кратных и дольных единиц
| Множитель | Приставка | Обозначение приставки | Множитель | Приставка | Обозначение приставки |
| экса | Э | деци | д | ||
| пета | П | санти | с | ||
| тера | Т | милли | м | ||
| гига | Г | микро | мк | ||
| мега | М | нано | н | ||
| кило | к | пико | п | ||
| гекто | г | фемто | ф | ||
| дека | да | атто | а |
Например, системная единица «метр» (м); кратная ей – «километр» (км), дольная – миллиметр «мм» (мм).
3.1 Классификация измерений
Измерение физической величины– совокупность операций по применению технического средства, хранящего единицу физической величины, обеспечивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения этой величины.
Измерения классифицируются по ряду признаков.
Признак 1.По общим приемам получения результатов измерений:
1) прямые –измерения, при которых искомое значение физической величины получают непосредственно. Примерами прямых измерений являются: измерения длины линейкой, т. е. путем сравнения искомой величины с мерой – линейкой и др.;
2) косвенные – измерения, при которых искомое значение величины определяют на основании результатов прямых измерений других физических величин, функционально связанных с искомой величиной. Например, мощность электрической цепи постоянного тока в соответствии с формулой P = I·U можно определить, проведя прямые измерения силы тока и напряжения;
3) совокупные – проводимые одновременно измерения нескольких одноименных величин, при которых искомые значения величин определяют путем решения системы уравнений, получаемых при измерениях этих величин в различных сочетаниях. Пример: значение массы отдельных гирь набора определяют по известному значению массы одной из гирь и по результатам измерений (сравнений) масс различных сочетаний гирь;
4) совместные– проводимые одновременно измерения двух или нескольких неодноименных величин для определения зависимости между ними.
Признак 2. По отношению к изменению измеряемой величины:
1) статические – измерения физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения. Пример: измерение длины детали при нормальной температуре;
2) динамические – измерения изменяющейся по размеру физической величины.
Признак 3. По числу измерений:
1) однократные – измерения, выполненные один раз;
2) многократные – измерения физической величины одного и того же размера, результат которых получен из нескольких следующих друг за другом измерений, т. е. состоящие из ряда однократных измерений.
Признак 4. По способу выражения результатов измерений:
2) относительные – измерения отношения величины к одноименной величине, играющей роль единицы, или измерение изменения величины по отношению к одноименной величине, принимаемой за исходную. Пример: измерение плотности жидкости ареометром;
Признак 5.По характеристике точности:
1) равноточные – ряд измерений какой-либо величины, выполненных одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью;
2) неравноточные – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерений и (или) в разных условиях.
Принципы измерений
Принцип измерений – это физическое явление или эффект, положенное в основу измерений. Рассмотрим лишь несколько широко распространенных эффектов.
1. Пьезоэлектрический эффект заключается в возникновении ЭДС на поверхности (гранях) некоторых кристаллов (кварц, турмалин, искусственные пьезоэлектрические материалы – пьезокерамики и др.) под действием внешних сил (сжатие, растяжение). Наибольшее применение для измерений нашли кварц и пьезокерамики (например, титанат бария), обладающие достаточно высокой механической прочностью и температурной стабильностью (кварц до температуры примерно 200 °С, пьезокерамика – до 115 °С). Пьезоэлектрический эффект обратим: ЭДС, приложенная к пьезоэлектрическому кристаллу, вызывает механические напряжения на их поверхности.
2. Термоэлектрический эффект широко применяется при измерениях температуры, причем используются две основных разновидности способов использования этого эффекта.
В первом используется свойство изменения электрического сопротивления металлов и полупроводников при изменении температуры. Из металлов часто применяются медь (для обычных измерений) и платина (для высокоточных измерений). Соответствующий измерительный преобразователь называется терморезистором. Чувствительные элементы полупроводникового преобразователя – термистора – изготавливаются из окислов различных металлов. С увеличением температуры сопротивление термистора уменьшается, в то время как у терморезистора – возрастает. Зависимость изменения сопротивления термисторов при изменении температуры существенно нелинейна, у медных терморезисторов – линейна, у платиновых аппроксимируется квадратным трехчленом. Платиновые терморезисторы позоляют измерять температуру в пределах от минус 200 до + 1000 °С.
Другим способом использования термоэлектрического эффекта является возникновение термо-ЭДС в замкнутом контуре, состоящем из двух разнородных проводников (или полупроводников), соединенных (спаянных) между собой на одном конце, а на другом подключенным к измерителю ЭДС, при различии температуры в месте спая и в месте соединения с измерителем. Соответствующие соединения двух разнородных проводников (полупроводников) называются термопарами. Широко используются для термопар хромель, копель, константан, платина и др. Термопары позволяют измерять температуру в широком диапазоне (от минус 200 до + 2800 °С). Например, пара хромель-константан позволяет измерять температуру до + 700 °С, а пара вольфрам-рений – до + 2800 °С. При этом приходится применять чувствительные измерители ЭДС, так как величина термо-ЭДС составляет от значений примерно 10 до 80 мкВ/°С.
3. Фотоэлектрический эффект. Для целей измерений используется внешний и внутренний фотоэффекты.
Внешний фотоэффект возникает в вакуумированном баллоне, имеющем анод и фотокатод. При освещении фотокатода в нем под влиянием фотонов света эмитируются электроны. В случае наличия между анодом и фотокатодом электрического напряжения эмитируемые фотокатодом электроны образуют электрический ток, называемый фототоком. Таким образом, происходит преобразование световой энергии в электрическую. Описанный преобразователь называется фотоэлементом. Существуют также газонаполненные фотоэлементы.
Внутренний фотоэффект возникает при освещении слоя между некоторыми полупроводниками и металлами. В этом слое возбуждается ЭДС. У ряда полупроводников под влиянием светового излучения изменяется электрическое сопротивление. Иногда этот эффект называется фоторезистивным, а соответствующие устройства – фоторезисторами. «Темновое» (при отсутствии освещения) сопротивление фоторезистора достаточно большое (например, 108 Ом). При освещении оно может уменьшиться до 105 Ом. Фоторезисторы обладают высокой чувствительностью, существенно превышающей чувствительность фотоэлементов. В качестве фоточувствительного материала применяют сернистый кадмий, сернистый свинец, кремний и др.
Методы измерений
Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений.
Методика выполнения измерений – установленная совокупность операций и правил при измерении, выполнение которых обеспечивает получение результатов измерений с гарантированной точностью в соответствии с принятым методом.
Методы измерений делятся:
1) метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений;
2) метод сравнения с мерой– метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой (пример: измерение массы на рычажных весах с уравновешиванием гирями (мерами массы с известным значением)). Методы сравнения реализуются следующими способами:
— дифференциальный метод измерений – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, и при котором измеряется разность между этими двумя величинами. Точность этого метода может быть высокой и определяется точностью величины, воспроизводимой мерой. Характерным примером дифференциального метода, иногда называемого методом неполного уравновешивания, является приведенный на рисунке 3.1. Вольтметр V включается с помощью переключателя П в цепь с измеряемым сопротивлением rx или в цепь с регулируемым потенциометром (мерой) r0. При достижении одинаковых показаний вольтметра (rx = r0) регистрируется искомое значение rx;
— нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля. Характерным примером нулевого метода является измерение активного сопротивления мостом постоянного тока (рисунок 3.2).
|
|
Мостовая схема оказывается полностью уравновешенной (гальванометр G показывает нуль), когда выполняется следующее условие: rxr2 = r1r3. Таким образом, при полном уравновешивании искомая величина rx = r1r3/r2;
— метод измерений замещением – метод сравнения с мерой, в котором измеряемую величину замещают мерой с известным значением величины. Пример: взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов (метод Борда);
— метод совпадений – метод сравнения с мерой, в котором разность между измеряемой величиной и известной величиной, воспроизводимой мерой измеряют, используя совпадения отметок шкал. Пример: измерение с помощью штангенциркуля.
ТЕМА 4. СРЕДСТВА ИЗМЕРЕНИЙ
Основные понятия о средствах измерений
Средство измерений – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.
Измерительное устройство – часть измерительного прибора (установки или системы), связанная с измерительным сигналом и имеющая обособленную конструкцию и назначение.
Показывающее устройство средства измерений – совокупность элементов средства измерений, которые обеспечивают визуальное восприятие значений измеряемой величины или связанных с ней величин.
Указатель средства измерений – часть показывающего устройства, положение которой относительно отметок шкалы определяет измерительное устройство показания средства измерений.
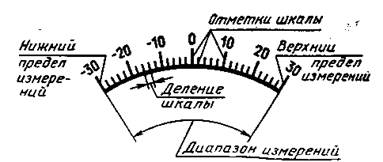
Шкала средства измерений – часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией (рисунок 4.1).
Рисунок 4.1 – Шкала средства измерений
Отметки на шкалах могут быть нанесены равномерно или неравномерно. В связи с этим можно выделить следующие виды шкал:
1) равномерная– шкала, длина делений которой не изменяется (рисунок 4.1);
2) практически равномерная – шкала, длина делений которой отличается друг от друга не более чем на 30 % и имеет постоянную цену делений;
3) неравномерная – шкала, длина делений которой отличается друг от друга более чем на 30 % и (или) имеет непостоянную цену делений;
4) существенно неравномерная– шкала с сужающимися делениями, для которой значение выходного сигнала, соответствующее полусумме верхнего и нижнего пределов диапазона изменений входного (выходного) сигнала, находится в интервале между 65 и 100 % длины шкалы, соответствующей диапазону изменений входного (выходного) сигнала;
5) степенная – шкала с расширяющимися или сужающимися делениями, отличная от шкал, указанных выше.
Деление шкалы – промежуток между двумя соседними отметками шкалы средства измерений (рисунок 4.1).
Длина деления шкалы – расстояние между осями (или центрами) двух соседних отметок шкалы, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы.
Цена деления шкалы – разность значения величины, соответствующих двум соседним отметкам шкалы средства измерений.
Диапазон измерений средства измерений– область значений величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений (рисунок 4.1).
Значения величины, ограничивающие диапазон измерений снизу и сверху (слева и справа) называют соответственно нижним и верхним пределами измерений (рисунок 4.1).