Что такое параллельный отрезок

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Параллельные прямые – две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные отрезки – два отрезка называются параллельными, если они лежат на параллельных прямых.

Параллельные лучи – два луча называются параллельными, если они лежат на параллельных прямых.

Теоретический материал для самостоятельного изучения.

Вы уже знаете, что на плоскости бывают пересекающиеся и непересекающиеся прямые, вы знаете, как их строить на чертеже. Теперь давайте рассмотрим прямые, которые называются параллельными, и научимся их строить различными способами.

Для начала дадим определение параллельным прямым.

Две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельные прямые имеют своё обозначение: a ║ b.

Рассмотрим прямые а и b, перпендикулярные прямой c. Ранее мы выяснили, что такие прямые не пересекаются, следовательно, прямые а и b параллельны.

Очень часто рассматриваются не только параллельные прямые, но и параллельные отрезки.

Дадим им определение.

Два отрезка называются параллельными, если они лежат на параллельных прямых.

Два луча называются параллельными, если они лежат на параллельных прямых.

Рассмотрим прямую с, пересекающую прямые а и b.

Прямая c называется секущей по отношению к прямым a и b, если она пересекает каждую из них.

Как видно из рисунка, при пересечении прямых а и b секущей c образуются 8 углов. Пронумеруем полученные углы.

Оказывается, некоторые пары образованных углов имеют свои названия.

Так, например, углы 3 и 5, 4 и 6 ‑ называются накрест лежащие углы.

Углы 4 и 5 или 3 и 6 ‑ называются односторонними углами.

А пары углов 1 и 5, 4 и 8, 2 и 6 или 3 и 7 ‑ называются соответственными углами.

Как же можно построить параллельные прямые?

Для построения параллельных прямых существует несколько способов построения с помощью различных чертёжных инструментов. Рассмотрим построение параллельных прямых с помощью чертёжного угольника и линейки.

Построим прямую b, проходящую через точку M и параллельную данной прямой а.

Приложим чертёжный угольник к прямой а, к нему приложим линейку. Теперь передвинем угольник вдоль линейки так, чтобы точка M оказалась на стороне угольника, остается провести прямую b. Прямые а и b будут параллельны, на основе признаков параллельности двух прямых, которые будут изучены позднее.

Материал для углублённого изучения темы

Другие способы построения параллельных прямых.

Рассмотрим ещё два способа построения параллельных прямых с помощью чертёжных инструментов.

В чертёжной практике очень часто используется способ построения параллельных прямых с помощью рейсшины.

При выполнении столярных работ, для разметки параллельных прямых используется ещё один инструмент – малка, который представляет собой две планки, скреплённые шарниром.

При нанесении параллельных рисок можно использовать рейсмус, который представляет собой деревянную заготовку с двумя регулируемыми брусками, на концах который прикреплены для нанесения рисок иглы или гвозди.

Разбор заданий тренировочного модуля

№ 1. Один из односторонних углов при двух параллельных прямых и секущей на 40º меньше другого. Найдите меньший угол, если известно, что сумма односторонних углов равна 180°.

Пусть х – меньший из односторонних углов, тогда больший равен х + 40. Т. к. сумма односторонних углов по условию равна 180°, составим уравнение.

х = 70° – градусная мера меньшего угла.

№ 2. Через параллельные прямые а и m проведены секущие АК и КР так, как показано на рисунке. КО = ВК = АК, при этом АК = КР = 9 см, отрезок ВО =АР, АР = 6 см. На сколько сантиметров периметр ∆ВОК меньше периметра ∆АКР?

Решение: найдём периметр ∆АКР.

Р_∆АКР = АК + КР + АР = 9 + 9 + 6 = 24 см

Найдём периметр ∆КВО. Для этого вычислим длины сторон треугольника КВО, исходя из условия задачи.

КО = ВК =АК = 9 = 6 см.

Р_∆КВО = ВК + КО + ВО = 6 + 6 + 4 = 16 см

Вычислим, на сколько периметр ∆ВОК меньше периметра ∆АКР.

Источник

Параллельность прямых

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение параллельности прямых

Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.

Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.

Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.

Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.

На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства и признаки параллельных прямых

Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.

Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.

Если секущая проходит через две параллельные прямые, то:

∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.

∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.

Если секущая образует перпендикуляр с одной из параллельных прямых, то она будет перпендикулярна и другой.

Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.

А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.

Задача 1

Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.

Решение

Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.

Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.

Задача 2

Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.

Решение

Поскольку а II b, значит ∠MKD + ∠KDN = 180°.

Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.

Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.

Источник

Параллельность и перпендикулярность

Параллельные прямые

Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их ни продолжали.

Через точку C проходит прямая, параллельная прямой AB. Двигай точки A, B и C.

Параллельные отрезки

Отрезки называются параллельными, если они лежат на параллельных прямых.

Отрезок CD параллелен отрезку AB. Двигай точки A, B, C и D.

Перпендикулярные прямые и отрезки

Перпендикулярные прямые — это прямые, образующие при пересечении прямые углы. Перпендикулярные отрезки — это отрезки, лежащие на перпендикулярных прямых.

Здесь прямые AB и CD перпендикулярны друг другу. Отрезки EF и GH перпендикулярны друг другу. Двигай точки A, B, C, E, F, G и H.

Перпендикуляр из точки к прямой

Перпендикуляр из точки к прямой – это отрезок, соединяющий точку с прямой, и перпендикулярный к этой прямой.

Здесь AB – прямая, а C – точка. И отрезок CD – это перпендикуляр из точки C к прямой AB. Двигай точки A, B и C.

Расстояние от точки до прямой

Расстояние от точки до прямой — это длина перпендикуляра, построенного от этой точки до этой прямой.

Здесь A — точка. EF — прямая. Расстояние от A до EF показывают ризки на перпендикуляре от A к EF. Двигай точки A, E и F.

Расстояние между параллельными прямыми

Расстояние между параллельными прямыми — это длина перпендикуляра, соединяющего эти прямые.

Здесь через точку A проходит прямая, параллельная прямой BC. Расстояние между прямыми показывают ризки на перпендикуляре. Двигай точки A, B и C.

Наклонная из точки к прямой

Наклонная из точки к прямой — это отрезок, соединяющий точку с прямой, и не перпендикулярный к этой прямой.

Здесь AB – прямая, а C – точка. И отрезок CD – это наклонная из точки C к прямой AB. Двигай точки A, B и C.

Источник

Параллельные прямые. Признаки параллельности прямых

Как мы знаем, прямые либо пересекаются (т.е. имеют одну общую точку), либо не пересекаются (т.е. не имеют ни одной общей точки).

Если прямые a и b параллельны, то это обозначают так:

На рисунке Рис.1 изображены прямые a и b, которые перпендикулярны к прямой c. В этом случае эти прямые не пересекаются (см. статью Перперндикулярные прямые), т.е. они параллельны (Определение 1).

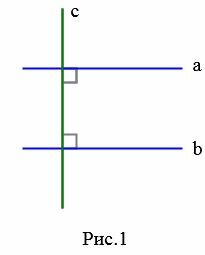Понятие параллельности можно распространять и на отрезки.

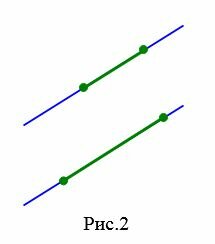Аналогично определяется параллельность отрезка и прямой, отрезка и луча, двух лучей, луча и прямой.

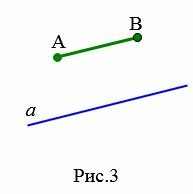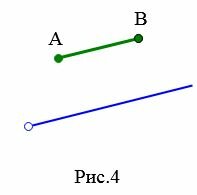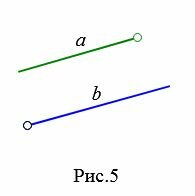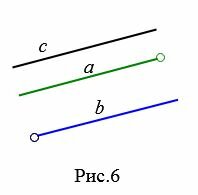На Рис.3 отрезок AB пераллелен к прямой a поскольку прямая, проходящай через отроезок AB параллельна прямой a. На рисунке Рис.4 отрезок AB пераллелен к лучу a так как прямые, проходящие через отрезок AB и луч a параллельны. Для Рис.5 и Рис.6 можно сделать аналогичные рассуждения.

Признаки параллельности прямых

Определение 3. Прямая c называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.

При пересечении прямой c с a и b образуются восемь углов, некоторые пары из которых имеют специальные названия (Рис.7):

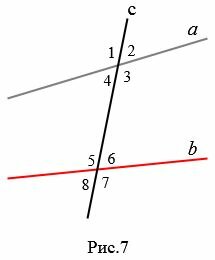Определим признаки параллельности двух прямых, связанные с этими парамы углов.

Теорема 1. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

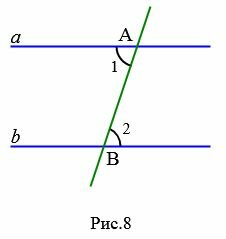
Доказательство. Предположим, что при пересечении прямых a и b секущей AB накрест лежащие углы равны: (Рис.8).

Докажем, что .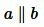

Если углы 1 и 2 прямые (Рис.9), то получается, что прямые a и b перпендикулярны прямой AB и, следовательно, они параллельны (теорема 1 статьи Перперндикулярные прямые и определение 1 настоящей статьи).

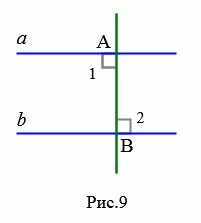Предположим, что углы 1 и 2 не прямые (Рис.10).

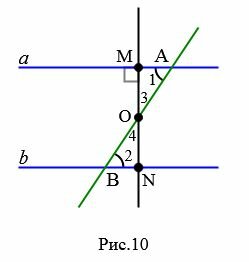Найдем середину отрезка AB и обозначим через O. Из точки O проведем перпендикуляр OM к прямой a. На прямой b отложим отрезок BN равной отрезку MA. Треугольники OAM и OBN равны по двум сторонам и углу между ними, так как OA=OB, MA=NB, . Тогда и .

означает, что точка N лежит на продолжении луча MO, т.е. точки M, O, N лежат на одной прямой. Угол BNO прямой (поскольку угол AMO прямой). Получается, что прямые a и b перпендикулярны к прямой MN, следовательно они параллельны.

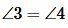
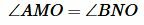
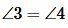
Теорема 2. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых a и b секущей с соответственные углы равны, например (Рис.11).

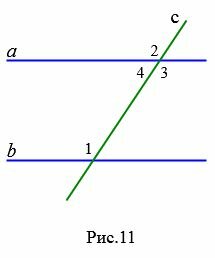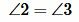
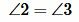
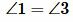
Так как углы 2 и 3 вертикальные, то . Тогда из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1, прямые a и b параллельны.

Теорема 3. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

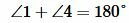
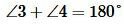
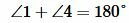
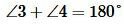
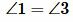
Доказательство. Пусть при пересечении прямых a и b секущей с сумма односторонних углов равна 180°, например (Рис.11). Из рисунка видно, что углы 4 и 3 смежные, т.е. . Из и следует, что . Но углы 1 и 3 накрест лежащие и, по теореме 1 прямые a и b параллельны.

Источник

Прямая линия. Параллельные прямые. Основные понятия.

Две прямые называются параллельными, если, находясь в одной плоскости, они не пересекаются, сколько бы их ни продолжали. Параллельность прямых на письме обозначают так: AB || СE

Возможность существования таких прямых доказывается теоремой.

Теорема.

Через всякую точку, взятую вне данной прямой, можно провести параллельную этой прямой.

Пусть AB данная прямая и С какая-нибудь точка, взятая вне ее. Требуется доказать, что через С можно провести прямую, параллельную AB. Опустим на AB из точки С перпендикуляр СD и затем проведем СE ^ СD, что возможно. Прямая CE параллельна AB.

Для доказательства допустим противное, т.е., что CE пересекается с AB в некоторой точке M. Тогда из точки M к прямой СD мы имели бы два различных перпендикуляра MD и MС, что невозможно. Значит, CE не может пересечься с AB, т.е. СE параллельна AB.

Следствие.

Аксиома параллельных линий.

Через одну и ту же точку нельзя провести двух различных прямых, параллельных одной и той же прямой.

Так, если прямая СD, проведенная через точку С параллельна прямой AB, то всякая другая прямая СE, проведенная через ту же точку С, не может быть параллельна AB, т.е. она при продолжении пересечется с AB.

Доказательство этой не вполне очевидной истины оказывается невозможным. Ее принимают без доказательства, как необходимое допущение (postulatum).

Следствия.

1. Если прямая (СE) пересекается с одной из параллельных (СВ), то она пересекается и с другой (AB), потому что в противном случае через одну и ту же точку С проходили бы две различные прямые, параллельные AB, что невозможно.

2. Если каждая из двух прямых (A и B) параллельны одной и той же третьей прямой (С), то они параллельны между собой.

Действительно, если предположить, что A и B пересекаются в некоторой точке M, то тогда через эту точку проходили бы две различные прямые, параллельные С, что невозможно.

Теорема.

Если прямая перпендикулярна к одной из параллельных прямых, то она перпендикулярна и к другой параллельной.

Перпендикуляр EF, пересекаясь с AB, непременно пересечет и СD. Пусть точка пересечения будет H.

Предположим теперь, что СD не перпендикулярна к EH. Тогда какая-нибудь другая прямая, например HK, будет перпендикулярна к EH и, следовательно через одну и ту же точку H будут проходить две прямые параллельные AB: одна СD, по условию, а другая HK по доказанному раньше. Так как это невозможно, то нельзя допустить, что СВ была не перпендикулярна к EH.

Источник