Что такое перестановочные матрицы
Матричное представление перестановок
Содержание
Матрица перестановок [ править ]
| Определение: |
| Матрица перестановок (англ. Permutation matrix) — квадратная бинарная матрица, в каждой строке и в каждом столбце которой находится лишь одна единица. |
Пусть дана перестановка [math]\sigma[/math] порядка [math]n[/math] :
[math]\begin
Соответствующей матрицей перестановки является матрица [math]n \times n[/math] вида:
Элементарная матрица перестановок [ править ]
| Определение: |
| Если матрица перестановок [math]P[/math] получена из единичной матрицы [math]E[/math] перестановкой местами двух строк (или двух столбцов), то такая матрица называется элементарной матрицей перестановок (англ. Elementary permutation matrix). |
Пример [ править ]
Применение [ править ]
Благодаря своим свойствам, матрицам перестановок нашлось применение в линейной алгебре. Они используются в элементарных преобразованиях матриц, то есть домножение слева или справа на матрицу перестановок, есть перестановка любых строк или столбов соответственно.
Свойства [ править ]
Теперь в обратную сторону [math]<(P^T P)>_
тогда перемножив получим:
СОДЕРЖАНИЕ
Определение
Учитывая перестановку π из т элементов,
представлен в двухстрочной форме
Характеристики
В этом разделе используется столбцовое представление матрицы перестановок, если не указано иное.
Умножение вектора-строки h раз переставит столбцы вектора: п π <\ displaystyle P _ <\ pi>>
Те же матрицы, действующие на векторы-строки (то есть после умножения), составляются по одному и тому же правилу
Для ясности, приведенные выше формулы используют префиксную нотацию для композиции перестановок, то есть
Из этого следует, что
Матричная группа
Дважды стохастические матрицы
Линейные алгебраические свойства
Примеры
Перестановка строк и столбцов
Перестановка строк
Объяснение
Матрица перестановок всегда будет иметь вид
является перестановка формы матрицы перестановок.
Таким образом, матрицы перестановок действительно меняют порядок элементов в векторах, умноженных на них.
Тема 1. «Матрицы и действия над ними» Основные понятия: Определение матрицы Виды матриц Действия над матрицами Перестановочные ма
Описание презентации по отдельным слайдам:
Описание слайда:
Тема 1. «Матрицы и действия над ними»
Основные понятия:
Определение матрицы
Виды матриц
Действия над матрицами
Перестановочные матрицы
Описание слайда:
1. Определение матрицы
Прямоугольная таблица чисел вида
называется матрицей.
— элементы матрицы.
Размер матрицы
Главная диагональ матрицы
Побочная диагональ матрицы
назад
Описание слайда:
Прямоугольная
Квадратная
Нулевая
Единичная
Диагональная
Симметричная
Вырожденная
Равные
Треугольная
Квазитреугольная (ступенчатая или трапециевидная)
Матрица-строка или строчная матрица
Матрица-столбец или столбцевая матриц
назад
Описание слайда:
Матрица называется прямоугольной, если количество ее строк не совпадает с количеством столбцов:
Матрица называется квадратной, если количество ее строк совпадает с количеством столбцов:
Описание слайда:
Матрица называется нулевой, если все ее элементы нулевые :
Квадратная матрица называется единичной, если элементы по главной диагонали единицы, а остальные элементы нулевые :
Описание слайда:
Квадратная матрица называется диагональной, если элементы по главной диагонали отличны от нуля, а остальные элементы нулевые:
Квадратная матрица называется симметричной, если относительно главной диагонали для всех ее элементов выполняется условие :
Описание слайда:
Квадратная матрица называется вырожденной, если ее определитель равен нулю.
Матрицы А и В (одинаковых размерностей) называются равными, если :
Описание слайда:
Квадратные матрицы вида
Описание слайда:
Прямоугольная матрица вида
называется квазитреугольной (ступенчатая или трапециевидная)
Описание слайда:
Матрица, состоящая из одной строки называется матрицей-строкой или строчной матрицей.
Матрица, состоящая из одного столбца называется матрицей-столбцом или столбцевой матрицей
Описание слайда:
Описание слайда:
Суммой (разностью) двух матриц одинаковой размерности называется матрица, элементы которой равны сумме (разности) соответствующих элементов матриц слагаемых.
Описание слайда:
Описание слайда:
Произведением матрицы на число называется матрица, полученная из данной умножением всех ее элементов на число.
Описание слайда:
Линейные операции обладают следующими свойствами:
Описание слайда:
Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей, транспонированной относительно данной.
Описание слайда:
Умножение матриц определяется для согласованных матриц.
Описание слайда:
Описание слайда:
В случае, когда АВ=ВА, матрицы А и В называют перестановочными или коммутативными.
Пример 1. Найти все перестановочные матрицы к матрице
Пример 2. Найти все перестановочные матрицы к матрице
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Свойства операции транспонирования:
Описание слайда:
Матрица А называется согласованной с матрицей В, если число столбцов матрицы А равно числу строк матрицы В:
Описание слайда:
Описание слайда:
Описание слайда:
Свойства операции умножение матриц:
1. Свойство сочетательности или ассоциативности
Свойство распределительности (дистрибутивности) справа и слева относительно сложения матриц
Описание слайда:
1) общий вид всех перестановочных матриц
2) Применим определение перестановочных матриц AB=BA:
Описание слайда:
3) По определению равных матриц
4) Общий вид всех перестановочных матриц
Описание слайда:
Описание слайда:
Спасибо за внимание!
Не забывайте готовиться к лекциям и семинарам!
(Тема следующей лекции «Определители»)
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Презентация «Как это было, как совпало – война, беда, мечта и юность!»
Памятка «Секреты эффективной похвалы»
Интегрированный урок окружающий мир и физкультура: «Океан, которого нет на карте. Закаливание воздухом»
Технология критического мышления » 6 шляп мышления»
Презентация «Развитие творческих способностей у младших школьников»
Виды занимательности при обучении грамоте
Определение в педагогике понятия «занимательность»
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5424133 материала.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Зарплаты педагогов Ростовской области вырастут в среднем на 10-15%
Время чтения: 2 минуты
АСИ организует конкурс лучших управленческих практик в сфере детского образования
Время чтения: 2 минуты
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Вопрос № 24. Определение операции умножения матриц. Примеры. Свойства умножения. Перестановочные матрицы. Примеры
Этих операций.
Вопрос № 23. Линейные (сложение и умножение на число) операции с матрицами Свойства
⊐ А и В – матрицы одинаковой размерности. Их суммой будет матрица той же размерности, эл-ты к-ой равны суммам эл-ов, стоящ.на соотв.местах
Cm+n= (Аm+n+ Bm+n) ⟷ (Cij=aij+bij)
A+B = 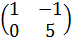

3) Существование нуля
⊐ 0: А+0=А
0 – нулевая матрица той же размерности, что и А. Матрица наз.нулевой, если все её эл-ты равны 0
Оm*n =
4) Существование противоположной матрицы
Умножение числа на матрицу
Произведением числа на матрицу будет матрица той же размерности, все элементы к-ой равны произв.k на соотв.эл-ты исходной матрицы.
(В=kA)⟷( 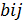
2∙ 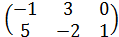
i ∙ 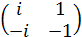
3∙
Умножение 2-х матриц: умножение А на В возможно тогда и только тогда, когда число столбцов А равно числу строк В; произведением матрицы А размера mxk на матрицу В размера kxn называется матрица С размера mxn, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы
Пр.: А∙В =
Св-ва умножения матриц:
В тех случаях, когда АВ=ВА, то говорят, что матрицы А и В перестановочные (они коммутируют).
Пр.: АВ =
ВА =
-1≠3⇒ АВ≠ВА
№25
Системы двух линейных ур-ий с двумя неизв. Имеют вид:
ax+by=c
dx=ey=f
где a,b,c,d,e,f-заданные числа,x,y-неизвестные.Числа
a,a,d,e-коэффициенты при неизвестных;с,f-свободые члены.Решение этой
системы может быть найдено двумя основными методами(подстановка,сложение
/вычетание)
Определители второго порядка,соотв. Данной матрице,наз.число,обознач.
символом
|a11 a12|
detA= | |
|a21 a22|
и определяемое рав-вом detA=a11a22-a12a21
Теорема. (Правило Крамера)
Теорема. Система из n уравнений с n неизвестными
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di =
A = 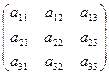


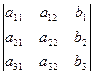
№26
Определители третьего порядка наз. число квадратной матрицы третьего
порядка,обозн. cимволом
|a11 a 12 a 13 |
A= |a21 a 22 a23 |
|a31 a32 a 33|
и определяемое рав-вом
detA=a11a22a33+a12a23a31+a13a21a32-a31a22a13-a21a12a33-a11a32a23
Диагональ,образ. эл-тами а11,а22,а33,наз. главной
Диагональ,образ. эл-тами а31,а22 и а13,наз. Побочной
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = ai 1 Ai 1 + ai 2 Ai 2 +. + ai n Ai n (i = 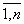
d = a1 j A1 j + a2 j A2 j +. + an j An j (j = 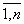
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Билет №27. Перестановки чисел 1,2,3. n. Инверсии. Подсчёт числа инверсий и четность-нечетность перестановки. Определители произвольного порядка.
Перестановка – упорядоченный набор чисел 1,2..n, трактуемый как биекция на множестве <1,2,…n>, в котором числу 1 ставят в соответствии i-тый элемент из набора N – порядок перестановки.
Перестановка является четной, если число инверсий четно. Нечетной, если число инверсий нечетно.
Инверсией в перестановке π порядка n называется всякая пара индексов i,j такая, что 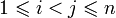
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Что такое перестановочные матрицы
Виктор Цекунов
Навигация
Affiliations
Template tips
2. Алгебра
___________________________________________________________________________
Оказываю платные услуги: решение задач по высшей математике. Оплата WebMoney.
Заказы направляйте сюда: Платные услуги
___________________________________________________________________________
2.1. Арифметика целых чисел.
2.2. Матрицы и определители.
2.3. Системы линейных уравнений.
2.4. Множества и отображения.
2.5. Комплексные числа.
2.8. Алгебраические уравнения.
2.9. Элементы теории полей.
2.10. Линейные пространства.
2.11. Линейные операторы.
2.12. Квадратичные формы.
2.1. Арифметика целых чисел.
2.1-1. Используя алгоритм Евклида сократить дробь: 169/448.
Решение:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после плюса стоят остатки):
448 = 169∙2 + 110,
169 = 110∙1 + 59,
110 = 59∙1 + 51,
59 = 51∙1 + 8,
51 = 8∙6 + 3,
8 = 3∙2 + 2,
3 = 2∙1 + 1,
2 = 1∙2.
Так как последний отличный от нуля остаток равен 1, то наибольший общий делитель чисел 448 и 169
НОД(448, 169) = 1.
Это означает, что числа 448 и 169 – взаимно простые. Следовательно, дробь
169/448 несократима.
2.1-2. Используя алгоритм Евклида сократить дроби: 490/1372; 92400/13960
Решение:
1) Д робь 490/1372:
Применяя алгоритм Евклида, получаем равенства (в правой части равенств после плюса стоят остатки):
1372 = 490∙2 + 392,
490 = 392∙1 + 98,
392 = 98∙4.
Так как последний отличный от нуля остаток равен 98, то наибольший общий делитель чисел 1372 и 490
НОД(1372, 490) = 98.
Сокращаем дробь на 98
(490:98)/(1372:98) = 5/14.
Вычислим M ₁.
M ₁ = 30636⁻¹ mod 13 или
30636 M ₁ mod 13=1,
30636 mod 13 · M ₁ mod 13=1,
8 · M ₁ mod 13=1, отсюда
8 M ₁ может принимать значения 14, 27, 40, …
Т.к. 40 делится на 8, то из уравнения
8 M ₁ = 40 находим
M ₁=40/8=5.
Вычислим M ₃.
M ₃ = 17316⁻¹ mod 23 или
17316 M ₃ mod 23=1,
17316 mod 23 · M ₃ mod 23=1,
20 · M ₃ mod 23=1, отсюда
20 M ₃ может принимать значения 24, 47, 70, 93, 116, 139, 162, 185, 208, 231,
254, 277, 300, …
Т.к. 300 делится на 20, то из уравнения
20 M ₃ = 300 находим
M ₃=300/20=15.
Вычислим M ₄.
M ₄ = 11063⁻¹ mod 36 или
11063 M ₄ mod 36=1,
11063 mod 36 · M ₄ mod 36=1,
11 · M ₄ mod 36=1, отсюда
11 M ₄ может принимать значения 37, 73, 109, 145, 181, 217, 253, …
Т.к. 253 делится на 11, то из уравнения
11 M ₄ = 253 находим
M ₄=253/11=23.
Подставим всё в (1)
x = (6 · 30636 · 5 + 33 · 10764 · 12 + 19 · 17316 · 15 + 14 · 11063 · 23) mod398268 =
= 13678970 mod398268 = 137858.
Ответ: x = 137858.
________________________________________________________________________________________________
2.2. Матрицы и определители.
2.2-2. Найдите все матрицы, перестановочные с матрицей
Решение:
Пусть матрица %20%D0%9C%D0%90%D0%A2.jpg)
АВ = ВА. (1)
Вычислим произведения матриц: АВ и ВА.
Итак, мы получили
det ( λA ) = λ ⁿ· detA и формула (1) доказана!
2. Из формулы (1) при n = 4, det A = 3 получаем
det 3 A = 3⁴· det A = 3⁴·3 = 3⁵= 243.
Ответ: det 3A = 3⁴·det A = 243.
2.3. Системы линейных уравнений.
2.3-2. Дана система уравнений:
Как выглядит базисное решение этой системы?
( к 2-й строке +3-ю строку, умноженную на (-2) )
( поменяем местами 2-ю и 3-ю строки )
2.3-4. Проверить, является ли система линейных уравнений
невырожденной, и решить её по формулам Крамера.
Решение:
1. Матрица А данной системы:
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= (к 3-й строке прибавим 2-ю строку, умноженную на 3) =
= (разложим определитель по 1-му столбцу) =
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
= ( к 2-й строке прибавим 1-ю строку, умноженную на (-1) ) =
= (разложим определитель по 1-му столбцу) =
2.5. Комплексные числа.
2.11. Линейные операторы.
Разложим определитель по 1-му столбцу
2.12. Квадратичные формы.
2.12-1. Как определить являются ли линейными преобразования каких-либо выражений?
________________________________________________________________________________________________
2.13. Тензоры.
2.13-1. Вычислить свертку Cijbkj+BmEikm






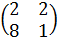
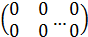
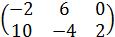
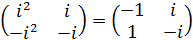



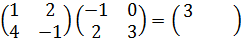
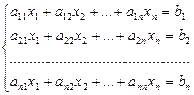
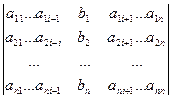
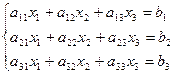

.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)
%20%D0%9C%D0%90%D0%A2.jpg)