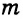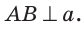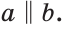Что такое перпендикуляр примеры

Перпендикулярные прямые в геометрии с примерами

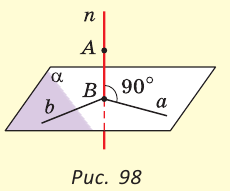
Определение: Две прямые называются перпендикулярными, если они пересекаются под прямым углом.

При пересечении двух перпендикулярных прямых образуются 4 прямых угла.

Отрезки и лучи называются перпендикулярными, если они лежат на перпендикулярных прямых. На рисунке 87 прямые

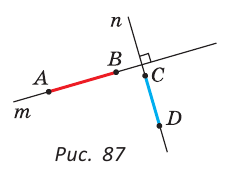
Определение. Перпендикуляром к данной прямой называется отрезок, который лежит на прямой, перпендикулярной данной, один из концов которого (основание перпендикуляра) является точкой пересечения этих прямых.

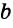
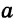
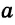
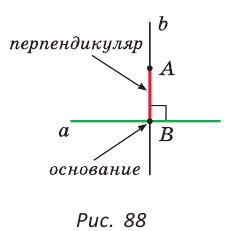
Прямая перпендикулярна прямой (рис. 88). Отрезок АВ — перпендикуляр к прямой , точка В — основание перпендикуляра. Точку В также называют проекцией точки А на прямую .

Если из точки М, которая не лежит на прямой , провести перпендикуляр МК к прямой (рис. 89), то получим перпендикуляр, опущенный из точки М на прямую . Если из точки Р, лежащей на прямой , провести перпендикуляр РЕ к прямой (рис. 90), то получим перпендикуляр, восстановленный (восставленный) к прямой .

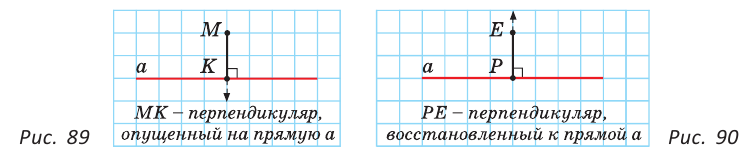
Теорема. Через точку, лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и только одну.

Дано: прямая ; точка А; (рис. 91).

Доказать: через точку А можно провести прямую, перпендикулярную прямой , и только одну.

Доказательство:

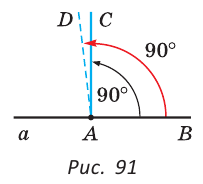
По аксиоме откладывания углов от луча АВ в данную полуплоскость можно отложить угол CAB, равный 90°, и притом только один. Тогда прямая АС перпендикулярна прямой . Предположим, что существует другая прямая AD, проходящая через точку А и перпендикулярная прямой . Тогда и от луча АВ в данную полуплоскость будут отложены два угла, равные 90°: А это невозможно по аксиоме откладывания углов. Следовательно, не существует другой прямой, проходящей через точку А и перпендикулярной прямой .

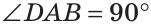
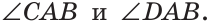
Теорема. Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой, и притом только одну.

Дано: прямая ; точка A, (рис. 92).

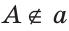
Доказать: через точку А можно провести прямую, перпендикулярную прямой , и притом только одну.

Доказательство:

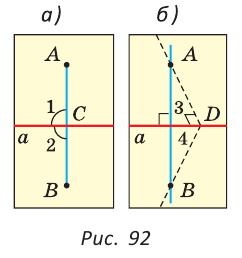
1) В начале докажем, что через точку А можно провести прямую, перпендикулярную прямой . Мысленно перегнем лист с чертежом по прямой (совместим верхнюю полуплоскость с нижней, повернув ее вокруг прямой ) (рис. 92, а). Точка А займет некоторое положение, которое обозначим точкой В. Вернем полуплоскости в прежнее положение и проведем прямую АВ. Так как углы 1 и 2 совпадают при наложении полуплоскостей, то они равны. А поскольку эти углы смежные, то каждый из них равен 90° и

2) Теперь докажем, что АВ — единственная прямая, проходящая через точку А и перпендикулярная прямой . Пусть прямая AD также перпендикулярна прямой . Тогда (рис. 92,6). Совместим полуплоскости еще раз. Угол 3 совпадет с углом 4, значит Тогда — развернутый, и через точки А и В будут проходить две прямые: ранее проведенная прямая и прямая, проходящая через точки A, D и В. А это невозможно по аксиоме прямой. Следовательно, прямая AD не перпендикулярна прямой . Теорема доказана.

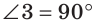
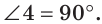
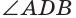
Из двух последних теорем следует, что на плоскости через любую точку можно провести прямую, перпендикулярную данной прямой, и притом только одну.

Теорема (о двух прямых, перпендикулярных третьей). На плоскости две прямые, перпендикулярные третьей, параллельны между собой.

Дано: 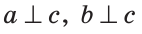(рис. 93).

Доказать:

Доказательство:

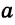
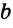
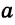
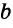
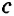
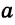
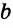
Если предположить, что прямые и пересекаются в некоторой точке М, то окажется, что через точку М проходят две прямые и , перпендикулярные третьей прямой , а это невозможно. Значит, прямые и лежат в одной плоскости и не пересекаются, то есть параллельны между собой. Теорема доказана.

Теорема, обратная данной

Если поменять условие и заключение теоремы местами, то получим утверждение, обратное данному. Для указанной выше теоремы получаем: «Если сумма двух углов равна 180°, то эти углы смежные». Но это утверждение неверно, поскольку можно привести пример двух углов, например, равных 60° и 120°, сумма которых 180°, но которые не являются смежными. Значит, приведенное утверждение не является теоремой.

Если же верно и обратное утверждение, то оно называется теоремой, обратной данной. Например, известна теорема: «Если сумма цифр числа делится на 3, то и число делится на 3» — и ей обратная: «Если число делится на 3, то и сумма цифр числа делится на 3».

Иногда прямую и обратную теоремы объединяют, употребляя при этом выражение «тогда и только тогда». Объединим вышеуказанные теоремы: «Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3».

Геометрия 3D

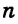
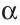
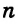
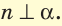
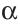
Пусть в пространстве прямая пересекает плоскость в точке В (рис. 98). Если прямая перпендикулярна любой прямой плоскости, проходящей через точку В, то она называется прямой, перпендикулярной плоскости. Пишут Отрезок АВ называется перпендикуляром к плоскости .

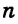
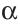
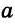
Чтобы прямая была перпендикулярна плоскости , достаточно, чтобы она была перпендикулярна каким-то двум прямым плоскости, проходящим через точку В. Например, прямым и .

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Определение перпендикулярных прямых, их свойства, характеристика

Содержание:

В геометрии существует понятие параллельных и перпендикулярных прямых. Ко вторым относится особый вид пересечения простейших геометрических фигур. Рассмотрим, какие прямые называются перпендикулярными. После теоретической выкладки материала научим правильно чертить такие чертежи при помощи угольника. Также разберёмся, что такое перпендикуляр к прямой, его свойства, обозначение.

Перпендикулярные прямые: определение, свойства

Теперь вы понимаете, что значит перпендикулярные прямые.
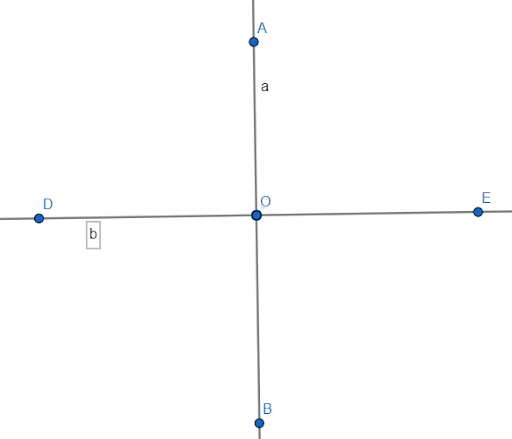
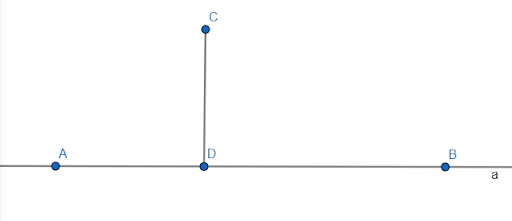
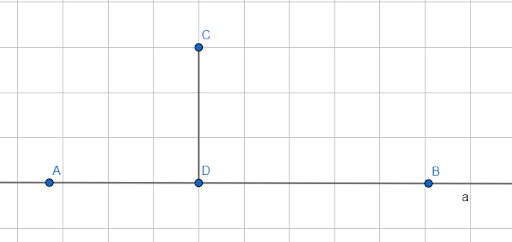
Дана линия a (AB) и не лежащая на ней точка C. Соединяющий их отрезок CD называется перпендикулярным, если отрезок CD образует с AB прямые углы. Точка D – основание перпендикуляра.

Способы построения

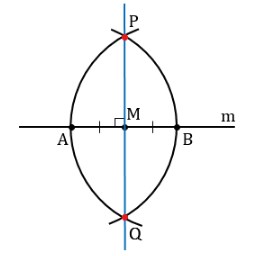
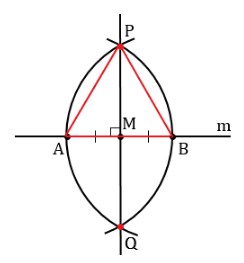
Второй способ сложнее. Дана линия m с лежащей на ней точкой M: M ∈ m. Построить отрезок PQ, проходящий через точку M и пересекающий m под прямым углом.

Теперь разберёмся, как доказать, что отрезки (прямые) перпендикулярны. Для этого рассмотрим треугольник APB или AQB (из условий задачи они одинаковые).

Две стороны простейшего многоугольника построены по радиусам одинаковых кругов, значит, они равны по длине – получаем равнобедренный треугольник, где AP = PB. Из условий задачи AM = BM, значит MP – медиана равнобедренного треугольника (исходя из определения этого термина). Отрезок PM – высота геометрической фигуры, она перпендикулярна основанию: PM ⟂ AB, что требовалось доказать.

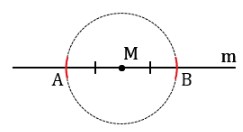
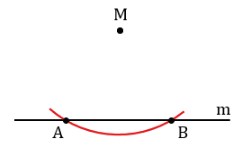
Проводим линию m и не лежащую на ней точку M. Рисуем окружность с центром M, пересекающую m в паре точек: A, B.

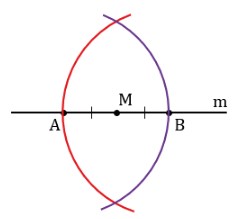
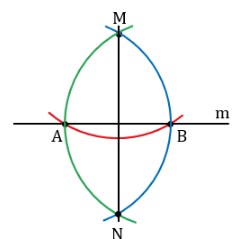
Чертим окружности с центрами в A и B, пересекающие M. Симметричную ей относительно прямой m точку обозначим N. Соединим их отрезком MN.

Докажем перпендикулярность MN линии m.

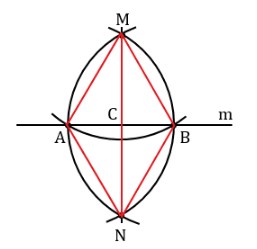
В треугольниках ANM с BNM равны стороны: AN = NB = AM = NB, AB – общая. Если три стороны треугольников равны, значит геометрические фигуры одинаковые: ∠АМС = ∠ВМС. Отрезки MC и CN – биссектрисы треугольников, где AB – основание. Далее, исходя из свойств равнобедренного треугольника, MC и CN – высоты геометрической фигуры, они перпендикулярны основанию. Получается, AB ⟂ MN.

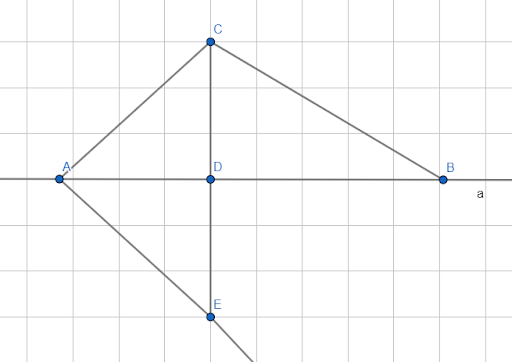
Задача

Мы доказали, что CE ⟂ a.
Последний шаг: покажем, что из точки C к прямой a нельзя провести более одного перпендикуляра.
Предположим: из точки С на прямую a возможно опустить второй перпендикуляр CD1. Тогда получим △CDD1 уже с парой прямых углов, что невозможно – у треугольника более одного прямого угла быть не может. Значит, из точки C нельзя опустить более одного перпендикуляра.
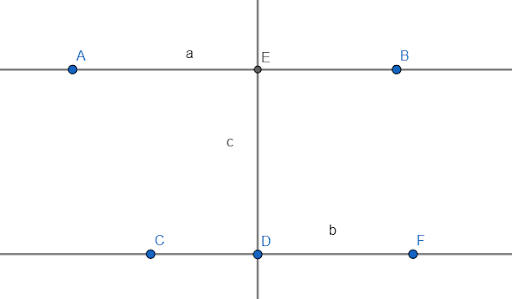
Исходя из рассмотренного материала, следует закономерное свойство двух прямых a и b, перпендикулярных к третьей c: между собой они параллельны: a||b.

Перпендикулярные отрезки – это отрезки, пересекающиеся под углом 90°.

Источник

Перпендикулярность

Содержание

На плоскости

Перпендикулярные прямые

Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.

В аналитическом выражении прямые, заданные линейными функциями и будут перпендикулярны, если выполнено условие . Эти же прямые будут перпендикулярны, если . (Здесь — углы наклона прямой к горизонтали)

Для обозначения перпендикулярности имеется общепринятый символ: , предложенный в 1634 году французским математиком Пьером Эригоном.

Построение перпендикуляра

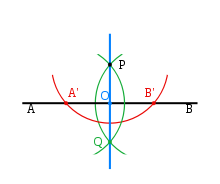
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В’.

Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В’ соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.

Координаты точки основания перпендикуляра к прямой

A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).

Если xa = xb (вертикаль), то xo = xa и yo = yp. Если ya = yb (горизонталь), то xo = xp и yo = ya.

Во всех остальных случаях

xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2); yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.

В трёхмерном пространстве

Перпендикулярные прямые

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим прямым, лежащим в одной плоскости и перпендикулярным в ней.

Перпендикулярность прямой и плоскости

Определение: Прямая называется перпендикулярной плоскости, если она перпендикулярна всем прямым лежащим в этой плоскости.

Признак: Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

В многомерных пространствах

Перпендикулярность плоскостей в 4-мерном пространстве

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости

Пусть задано n-мерное евклидово пространство (n>2) и ассоциированное с ним векторное пространство , а прямая l с направляющим векторным пространством и гиперплоскость с направляющим векторным пространством (где , ) принадлежат пространству .

Прямая l называется перпендикулярной гиперплоскости , если подпространство ортогонально подпространству , то есть

Источник

Значение слова «перпендикуляр»

[От лат. perpendicularis — отвесный]

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

ПЕРПЕНДИКУЛЯ’Р, а, м. [латин. perpendicularis — отвесный] (мат.). Прямая линия, составляющая прямой угол с данной прямой. Опустить из какой-н. точки п. на линию, на плоскость. Восставить п. какой-н. линии из какой-н. точки ее. П. к линии. П. к плоскости.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

перпендикуля́р

1. геометр. прямая линия, пересекающая какую-либо прямую под прямым углом (в 90 градусов)

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я стал чуточку лучше понимать мир эмоций.

Вопрос: излазить — это что-то нейтральное, положительное или отрицательное?

Ассоциации к слову «перпендикуляр&raquo

Синонимы к слову «перпендикуляр&raquo

Предложения со словом «перпендикуляр&raquo

Понятия, связанные со словом «перпендикуляр»

Отправить комментарий

Дополнительно

Предложения со словом «перпендикуляр&raquo

Для определения суточных потребностей в воде и электролитах восстанавливают перпендикуляр от показателя возраста или массы больного до пересечения с неправильной кривой в средней части номограммы.

Это разметочный инструмент, который применяют для измерения длины на чертежах, деления углов, прямых линий для вычерчивания окружностей, построения перпендикуляров.

По центру поставим засечку и поднимем вверх перпендикуляр, на котором отложим длину юбки по боку.

Источник