Что такое сопряженная величина

Большая Энциклопедия Нефти и Газа

Канонически сопряженная величина

Канонически сопряженные величины относятся к общей категории одновременно неизмеряемых величин, коммутатор которых равен постоянной. Но имеется также другая категория одновременно неизмеряемых величин, коммутатор которых равен отличному от нуля оператору. [1]

Рассмотрим две канонически сопряженные величины х и, рх. [2]

К числу канонически сопряженных величин относятся энергия и время. [3]

Мы рассмотрели возможность одновременного измерения двух канонически сопряженных величин и показали, что точность таких измерений всегда ограничена соотношениями Гейзенберга. Но сопряженные величины относятся к первой категории некоммутирующих величин: для них коммутатор постоянен. Можно ли прийти к аналогичным выводам для некоммутирующих величин второго рода, для которых коммутатор равен ненулевому оператору. [7]

Соотношения Гейзенберга имеют место для любой пары канонически сопряженных величин ( стр. [8]

Таким образом, точность одновременного определения двух канонически сопряженных величин регулируется принципом неопределенности, что было впервые установлено В. Гейзенбергом ( 1927), который писал: Никогда нельзя одновременно точно знать оба параметра, решающим образом определяющие движение такой мельчайшей частицы: ее место и ее скорость. Никогда нельзя одновременно знать, где она находится, как быстро и в каком направлении движется. Если ставят эксперимент, который точно показывает, где она находится в данный момент, то движение нарушается в такой степени, что частицу после этого нельзя даже снова найти. [9]

Таким образом, точность одновременного определения двух канонически сопряженных величин регулируется принципом неопределенности, что было впервые установлено В. Гейзенбергом ( 1927), который писал: Никогда нельзя одновременно точно знать оба параметра, решающим образом определяющие движение такой мельчайшей частицы: ее место и ее скорость. Никогда нельзя одновременно знать, где она находится, как быстро и в каком направлении движется. Если ставят эксперимент, который точно показывает, где она находится в данный момент, то движение нарушается в такой степени, что частицу после этого нельзя даже снова найти. [10]

На нескольких примерах мы показали, что анализ измерения двух канонически сопряженных величин приводит к соотношениям Гейзенберга. [13]

Это связано с тем, что при движении частицы в магнитном ( электромагнитном) поле канонически сопряженными величинами являются координата ( обобщенная в общем случае) и обобщенный импульс. [15]

Источник

Канонически сопряженные величины (КСВ)

КАНОНИЧЕСКИ СОПРЯЖЕННЫЕ ВЕЛИЧИНЫ (КСВ)

Все познается на примерах. Начну объяснение с бытовых примеров.

Например, если человек внешне всегда грязный, зато внутри всегда чистый. А если человек снаружи чистый, значит внутри грязный. Произведение этих величин – величина постоянная. А сами эти величины называются КСВ. Правда, великий медик сказал, что в человеке должно быть все чисто: снаружи и внутри. Жаль, что он не знал физику. Зато в медицине первым понял, что нужно лечить не болезни, а человека, т. е. устранять причины болезней, а болезни сами пройдут.

Для лучшего объяснения такого квантового явления, как принцип неопределенности Гензенберга, приведу еще несколько КСВ: богатство и порядочность, красота и характер, сила и ум (сила есть – ума не надо), энергия и время, координата и импульс и др. Общая формула всех КСВ:

где ai и bk есть КСВ, а cl – константа.

Теперь если вместо ai подставим наименьшее деление шкалы длины –ΔX, вместо bk – наименьшее деление шкалы импульсов – ΔP, а вместо cl – постоянную Планка, то получим уравнение принципа неопределенности:

Но это еще не все. Все физические величины можно представить как произведение трех основных величин – массы, длины и времени с соответствующими показателями степени:

Удобная запись Δ (0 + 1+ 0) + (1 + 1 – 1) = (1 + 2 – 1).

Теперь можно по-другому сгруппировать величины и получим еще одно уравнение неопределенности:

где: Е – энергия, Т – время.

Снова разложим на основные величины и получим:

(1 + 2 – 2) + (0 + 0 + 1) = (1 + 2 – 1)

В отличие от одномерных шкал, например длины, шкала принципа неопределенности – двухмерная. Наглядно это будет лист бумаги, где вдоль одной стороны нанесены деления длины –Δ X, а на перпендикулярной стороне – деления импульсов –Δ Р. Поскольку произведение ΔХ ΔР является предельно малой площадью, равной постоянной Планка, то если Вы захотите точно измерить координату, то при той же площади, создав мелкие деления длины, деления импульсов окажутся очень большими, которыми не сможете точно измерить импульс, и наоборот. Это и есть квантовая принципиальная невозможность измерить обе КСВ.

Учёные открыли дуализм корпускулярно-волновой,

Но дуализмов существует очень много.

Мышление и чувства – это тоже дуализм как таковой:

В мозгах он разделяется на «левое» и «правое» довольно строго.

Часть учёных доказывала, что свет состоит из частиц (корпускул). Другая часть доказывала, что свет состоит из волн. Но оказалось, что чем короче волна, тем она больше похожа на частицу. Так появился первый дуализм корпускулярно-волновой. Я увидел дуализм во многих явлениях природы. Например, «разум-интуиция». Это когда разум требует одно, а интуиция – другое. У кого больше развит разум (левое полушарие мозга), те больше доверяют разуму. У кого больше развита интуиция (правое полушарие мозга), те больше доверяют ей. Левополушарными являются учёные, которые информацию разделяют на отдельные элементы, анализируют их и дают точный ответ. Военным командирам, руководителям крупных предприятий некогда этим заниматься и они не точно, зато быстро принимают интуитивные решения. Это дуализм №2.

Дуализм №8 – это когда мои статьи можно воспринимать одновременно как в шутку, так и всерьёз.

Каждый человек с первого дня рождения начинает заниматься наукой. Наука в моём понимании не теория известного учёного, а с помощью обобщения опытов создаётся модель мира, которая снова проверяется опытом и совершенствуется и снова проверяется опытом и т. д. А догмы знаменитостей не являются наукой. Ребёнок в первый же день начинает исследовать окружающее пространство с помощью рук, глаз и голоса и строит свою модель мира. И в течении всей жизни совершенствует свою модель. Эта модель является программой поведения человека. На основе тестового опроса можно предвидеть, что ожидать от такого человека.

Источник

Большая Энциклопедия Нефти и Газа

Канонически сопряженная величина

Поскольку с макроскопической точки зрения постоянная Планка Л пренебрежимо мала, в макроскопических явлениях одновременное измерение двух канонически сопряженных величин оказывается практически возможным, ибо в этом случае неточность измерения намного превышает квантовые неопределенности. Но в масштабе явлений, затрагивающих элементарные частицы, величиной Л пренебречь нельзя, а потому квантовые неопределенности играют существенную роль. [16]

Покажем, что, если физическим величинам соответствуют некоммутирующие друг с другом операторы, в рамках квантовой механики они не могут быть одновременно вычислены точно. Наиболее важным в этом отношении является вычисление отклонения от средних значений операторов двух канонически сопряженных величин : координаты х и импульса рх. [24]

Из соотношения неопределенности вытекает, что в рамках квантовой механики невозможно точно теоретически предсказать для одного и того же момента времени и координату, и импульс электрона. Сторонники интерпретации квантовой механики в духе принципа дополнительности пытаются это объяснить особым влиянием на микромир макроприборов, воздействие которых при одновременном измерении двух канонически сопряженных величин ( например, координаты и импульса электрона) нельзя сделать сколь угодно малым. Возводя это в особый принцип, они приходят к выводу, что должен существовать некий конечный предел познания микромира. Таким образом, принцип дополнительности скорее носит мировоззренческий характер и имеет примерно такое же отношение к квантовой механике, какое в свое время имело механистическое мировоззрение к классической механике. [25]

Но можно поставить вопрос, действительно ли невозможно одновременно измерить две канонически сопряженные физические величины и какова физическая причина такой невозможности. Тонкий анализ, проведенный Бором и Гейзенбергом, показал, что на самом деле невозможно представить себе опыт, который позволил бы одновременно измерить две канонически сопряженные величины с точностью, превышающей ту, которую допускают соотношения неопределенностей Гейзенберга. Долгая дискуссия, зачинателями которой были Бор и Гейзенберг, закончилась в их пользу, и в настоящее время их утверждения, по-видимому, приняты всеми физиками, серьезно изучавшими данный вопрос. [26]

Как было показано выше, согласно положениям волновой механики, невозможно одновременно точно измерить две некоммутирующие наблюдаемые, в частности две канонически сопряженные величины. Это оказывается следствием фундаментального постулата о том, что состояние наших знаний о системе должно характеризоваться волновой функцией ф как до, так и после измерения. Если бы две канонически сопряженные величины можно было одновременно измерить точно, то состояние системы после измерения нельзя было бы характеризовать волновой функцией ф и от волновой механики пришлось бы отказаться. [28]

Согласование состоит в том, что требуемое изменение величины МЕм разделяют на два равных относительных изменения, осуществляемых на расстоянии в 1 / 4 периода фазовых колебаний одно от другого. Большое значение в понимании рассмотренных выше, а также описываемых в дальнейшем преобразований пучка имеет теорема Лиувилля. Эта теорема утверждает, что при движении системы, характеризуемой канонически сопряженными величинами ( обобщенными координатами и импульсами), объем данного участка фазового пространства, а также сумма частных фазовых объемов остаются неизменными. [30]

Источник

сопряженная величина

Смотреть что такое «сопряженная величина» в других словарях:

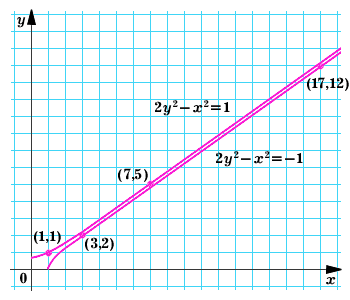
Гипербола (математика) — У этого термина существуют и другие значения, см. Гипербола. Гипербола и её фокусы … Википедия

ГОСТ 25142-82: Шероховатость поверхности. Термины и определения — Терминология ГОСТ 25142 82: Шероховатость поверхности. Термины и определения оригинал документа: 1.16. Базовая длина l Длина базовой линии, используемая для выделения неровностей, характеризующих шероховатость поверхности (черт. 12) Черт. 12 1.17 … Словарь-справочник терминов нормативно-технической документации

ГРИНА ФУНКЦИЯ — функция, связанная с интегральным представлением решений краевых задач для дифференциальных уравнений. Г. ф. краевой задачи для линейного дифференциального уравнения фундаментальное решение уравнения, удовлетворяющее однородным краевым условиям.… … Математическая энциклопедия

Железные дороги — I I. История развития железных дорог. Ж. дорога, в том виде, в каком она существует теперь, изобретена не сразу. Три элемента, ее составляющие, рельсовый путь, перевозочные средства и двигательная сила прошли каждый отдельную стадию развития,… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ГОСТ 23070-78: Анализ и оптимизация на ЭВМ радиоэлектронных схем. Термины и определения — Терминология ГОСТ 23070 78: Анализ и оптимизация на ЭВМ радиоэлектронных схем. Термины и определения оригинал документа: Многовариантный анализ 32. Анализ переходных процессов радиоэлектронной схемы Одновариантный анализ, при котором получают… … Словарь-справочник терминов нормативно-технической документации

Гиперболы — Под этим названием известен в аналитической геометрии ряд кривых линий. 1) Г. второго порядка, или так называемая Аполлониева гипербола. Эта кривая линия была известна уже грекам и принадлежит к числу конических сечений, т. е. получается через… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

ТЕРМОДИНАМИКА НЕОБРАТИМЫХ ПРОЦЕССОВ — (неравновесная термодинамика), изучает общие закономерности поведения систем, не находящихся в состоянии термодинамического равновесия. В таких системах имеют место разнообразные неравновесные процессы (теплопередача, диффузия, электрич. ток, хим … Химическая энциклопедия

Реакции нуклеофильного замещения — (англ. nucleophilic substitution reaction) реакции замещения, в которых атаку осуществляет нуклеофил реагент, несущий неподеленную электронную пару.[1] Уходящая группа в реакциях нуклеофильного замещения называется нуклеофуг. Все … Википедия

ЧТО ТАКОЕ РАСТЕНИЕ — Общая площадь планеты Земля составляет 510 млн. км2. На долю суши приходится 149 млн. км2, Мировой океан занимает 361 млн. км2. И суша и океан заселены растениями и животными. Разнообразие и тех и других очень велико. Ныне установлено… … Биологическая энциклопедия

Адиабатический инвариант — Адиабатический инвариант физическая величина, которая не меняется при плавном, «адиабатическом», изменении некоторых параметров физической системы. Адиабатичнисть изменения параметра означает, что характерное время этого изменения гораздо… … Википедия

ГОСТ Р 53784-2010: Элементы оптические для световых сигнальных приборов железнодорожного транспорта. Технические условия — Терминология ГОСТ Р 53784 2010: Элементы оптические для световых сигнальных приборов железнодорожного транспорта. Технические условия оригинал документа: 3.19 выборка: Выборка из партии по случайному признаку, состоящая из одной или более единиц… … Словарь-справочник терминов нормативно-технической документации

Источник

Что такое сопряженная величина

Читателю, вероятно, известны на первый взгляд трудные геометрические задачи, которые мгновенно решаются, если заменить одну данную точку другой, симметричной ей относительно прямой. Соображения симметрии очень важны и в алгебре.

В этой статье мы рассмотрим ряд ситуаций, в которых число вида полезно заменить сопряжённым Мы увидим, как этот простой приём — замена знака перед радикалом — помогает в решении разнообразных задач алгебры и анализа — от нехитрых оценок и преобразований до трудных олимпиадных задач и замысловатых придумок составителей конкурсных экзаменов.

Большинство наших примеров может служить первым знакомством с глубокими математическими теориями мы указываем статьи и книги для продолжения знакомства). Среди задач, включённых в статью, две — из Задачника «Кванта» и несколько — из писем читателей, уже испытавших удовольствие от трюков с радикалами и желающих поделиться им с другими.

Пары сопряжённых чисел появляются вполне естественным образом, когда мы решаем квадратное уравнение, а корень из дискриминанта не извлекается: скажем, уравнение имеет пару «сопряжённых» корней:

К этому мы ещё вернёмся, а начнём с примеров другого рода: займёмся «перебросками».

Если в книжке указан ответ к задаче а у вас получилось — не спешите искать ошибку в решении: ответ правильный — эти числа равны, потому что

Вот несколько характерных примеров, где полезно перенести «иррациональность» из числителя в знаменатель или наоборот.

Эта сумма мгновенно «сворачивается», если переписать её так:

По выражению из статьи [1] «остаются крайние» (см. также [5]).

2. Доказать, что для любых натуральных m и n

Подобный факт мы использовали недавно при решении трудной задачи

В самом деле, всегда

поскольку число — целое и отлично от 0 (равенство невозможно — подумайте, почему!). Если бы выполнялось неравенство, противоположное (1), то должно было бы быть и

n ( m + n √ 2 ) n ( 2 n √ 2 + 1 Но из (2) и (3) следует (1). Значит, наше предположение неверно, то есть (1) выполнено. Оно лишь немного сильнее, чем неравенство (1), поскольку π = 0,3183. > 0,3178. = 1 зато выглядит гораздо эффектнее. Помню как в мою бытность студентом на лекциях по алгебре наш профессор говорил: «Корень из это, примерно, 1,73; корень из 1,41. Поэтому их сумма равна. (следовала пауза, необходимая для сложения этих чисел 3,14. (он поворачивался к аудитории и сразу несколько человек с удовлетворением заключал профессор, выписывая окончательное «равенство»: 🙂 ] 3. Найдите предел последовательности Преобразуем a n так: Теперь ясно, что a n возрастает и стремится к В противоположность предыдущему примеру здесь мы имеем дело с хорошим приближением: 4 (M532). Даны две последовательности и Докажите, что В разности появляется «тройная иррациональность»; к таким иррациональностям мы ещё вернёмся (см. задачу 8), но пока мы будем рассматривать как одно целое. Заметим, что величина очевидно, заключена между и поскольку Итак, мы уже получили — левое неравенство Кроме того, число дающее при делении на 4 в остатке 2, не может быть полным квадратом (проверьте!), поэтому квадрат целого числа не больше из неравенств Теперь осталось оценить разность сверху. Посмотрите, как здесь дважды работает переброска «сопряжённого» числа в знаменатель: √ 4 n +2 – √ n – √ n +1 = 2 n + 1 – 2√ n ( n + 1) √ 4 n + 2 + √ n + √ n + 1 = = 1 (√ 4 n + 2 + √ n + √ n + 1 )(2 n + 1 + 2√ n ( n + 1) ) ≤ ≤ 1 (2√ n + √ n + √ n )(2 n + 2 n ) = 1 Заметим, что и эта оценка очень точная. Но убедиться в этом (и вообще исследовать поведение функции с многими радикалами) лучше уже не с помощью алгебраических преобразований, а средствами анализа — заменить переменную n на и воспользоваться формулой Тейлора Мы уже говорили о пользе симметрии в геометрических задачах. Своего рода симметрией в алгебре является замена плюса на минус. Так, если какое-либо выражение от равно и мы всюду в этом выражении заменим на то естественно ожидать, что новое выражение окажется равным сопряженному числу Мы будем пользоваться таким очевидным частным случаем этого свойства ( a и b — рациональны, — нет): 5. Доказать, что уравнение не имеет решений в рациональных числах x, y, z, t. Можно, конечно, найти отдельно сумму членов левой части, не содержащих (она должна быть равна 2), и отдельно — коэффициент при (он должен равняться 1). Но что делать с полученной громоздкой системой неясно. Вместо этого воспользуемся (4) и заменим плюс перед на минус! Слева стоит неотрицательное число, справа — отрицательное. 6. Доказать, что существует бесконечно много пар натуральных чисел, для которых x 2 отличается от 2 y 2 Несколько таких пар с небольшими легко найти подбором: это (1; 1), (3; 2), (7; 5), (рис. 1). Как продолжить этот набор? Можно ли записать общую формулу для этих решений? Рис. 1. Проходят ли эти гиперболы через бесконечное число узлов клетчатой бумаги? Найти ответы на эти вопросы нам поможет число Закономерность, позволяющая получать всё новые и новые решения указана в таблице: n (1 + √ 2 ) n x n y n x n 2 – 2 y n 2 (1 – √ 2 ) n 1 1 + √ 2 1 1 1 – 2 = –1 1 – √ 2 2 3 + 2√ 2 3 2 9 – 8 = 1 3 – 2√ 2 3 7 + 5√ 2 7 5 49 – 50 = –1 7 – 5√ 2 4 17 + 12√ 2 17 12 289 – 288 = 1 17 – 12√ 2 5 41 + 29√ 2 41 29 1681 – 1682 = –1 41 – 29√ 2 . . . . . . Какой будет шестая строчка? будут давать нужную пару. Доказать это поможет колонка таблицы из сопряжённых чисел (мы снова Перемножив два последних равенства, получим и интересующее нас выражение попеременно равно то 1, то Складывая и вычитая эти же два равенства, мы получим явное выражение для x n и y n : Освободитесь от иррациональности в знаменателе: Источник ← Что такое сальдо в расчетном листке зарплаты Что такое перпендикуляр примеры → Вам также понравится Что такое демодекс на лице 26.10.202316.04.2022 admin 0 Что такое субсидиарка при банкротстве 26.10.202304.05.2022 admin 0 Что такое пэт банка 29.10.202323.04.2022 admin 0 Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев. x n = (1 + √ 2 ) n + (1 – √ 2 ) n 2 , y n = (1 + √ 2 ) n – (1 – √ 2 ) n Можно ли в решении этой задачи про целые числа обойтись без иррациональных чисел и Теперь, зная ответ, мы можем легко выразить через предыдущую пару из ( x n + y n √ 2 )(1 + √ 2 ) вытекает До этого рекуррентного соотношения можно было, видимо, догадаться по нескольким первым решениям, а потом проверить, что Рекуррентные соотношения типа (6) возникают не только в теории чисел, но и в разных задачах анализа, теории вероятностей. Вот характерный пример комбинаторной задачи такого типа (она предлагалась на последней международной олимпиаде в Лондоне): 7 (М595). В вершине A правильного восьмиугольника сидит лягушка. Из любой вершины восьмиугольника, кроме вершины E, противоположной A, она может прыгнуть в любую из двух соседних вершин. Попав в E, лягушка останавливается и остаётся там. Найти количество e m различных способов, которыми лягушка может попасть из вершины A в E ровно за m прыжков. А интересующее нас число e 2 n равно, очевидно, а) c 1 = 1 б) a 1 = 2 в) a n +1 = 2 a n + 2 c n г) c n +1 = a n + 2 c n д) e 2 n = 2 c n –1 Из A в C за два прыжка можно попасть только одним способом: Из A в A за два прыжка можно попасть двумя способами: В A можно попасть из C двумя способами и из A двумя способами: В C можно попасть из A одним способом и из C — двумя: В E можно попасть из C двумя способами: Рис. 2. а) б) в) г) д) a n +1 + c n +1 √ 2 = ( a n + c n √ 2 )(2 + √ 2 ) (8) и — как вы уже, конечно, догадались — ещё так: a n +1 – c n +1 √ 2 = ( a n – c n √ 2 )(2 – √ 2 ). (9) Отсюда по индукции, пользуясь (7), получаем: Докажите, что последовательность содержит бесконечно много квадратов целых чисел. Составьте квадратное уравнение с целыми коэффициентами, один из корней которого Составьте уравнение 4-й степени с корнями и решите его, как биквадратное уравнение. Сравнивая ответ с данными корнями, докажите популярные формулы для двойных радикалов: c n = (2 + √ 2 ) n – (2 – √ 2 ) n а так как получаем окончательно Докажите, что функция — нечётная, и постройте её график. а) Докажите, что для любого натурального n б) Докажите, что последовательность убывает и стремится к пределу. а) Докажите, что последовательность сходится, и найдите её предел. б) Каковы первые 100 десятичных знаков после запятой в записи числа 2 + √ 2 + p e 2 n = (2 + √ 2 ) n –1 – (2 – √ 2 ) n –1 Задача решена. Неясно только, как в этой задаче (и в предыдущей задаче 6) можно было додуматься до формул, содержащих — ведь в задаче речь идёт о целых числах! (Для участников олимпиады и читателей «Кванта» задача 7 была облегчена тем, что в формулировке указывался ответ — «Квант», 1979, № 11, М595 ). Однако «сопряжённые числа» возникли бы совершенно автоматически, если бы мы владели началами линейной алгебры (см. [12]), и применили стандартные правила этой науки к решению уравнений (7). Эти правила предлагают сначала выяснить, какие геометрические прогрессии удовлетворяют данному рекуррентному соотношению. Значения, для которых такие прогрессии существуют, — они называются характеристическими значениями или собственными числами — определяются из некоторого уравнения (оно тоже называется характеристическим ). Для (7) характеристическое уравнение имеет вид его корни — как раз и Зная эти корни, любое решение рекуррентного соотношения мы можем получить как «линейную комбинацию» соответствующих геометрических прогрессий ([11]). «Начальное условие» (в нашем случае определяет нужное нам решение однозначно. Неудивительно, что даже самые простые рекуррентные целочисленные последовательности, для которых характеристическое уравнение — квадратное с целыми коэффициентами (примеры — те же (6) и (7) или последовательность Фибоначчи 1, 1, 2, 3, 5, см. [9], [10]), выражаются, как функции номера, с помощью «сопряжённых» квадратичных иррациональностей. Интересное продолжение этого факта мы увидим в следующей задаче с бо́льшим числом «сопряжённых» иррациональностей. Конечно, мы здесь можем выразить через ( q n ; r n ; s n ; t n ), пользуясь тем, что Нетрудно сообразить, каковы будут другие. Рассмотрим вместе с данным числом ещё три «сопряжённых»: Докажите, что при всех положительных x Постройте график функции и докажите, что при q n = λ 1 n + λ 2 n + λ 3 n + λ 4 n 4 , s n = λ 1 n + λ 2 n – λ 3 n – λ 4 n 4√ 3 , r n = λ 1 n – λ 2 n + λ 3 n – λ 4 n 4√ 2 , t n = λ 1 n – λ 2 n – λ 3 n + λ 4 n Теперь заметим, что Поэтому 1 + (λ 2 /λ 1 ) n + (λ 3 /λ 1 ) n + (λ 4 /λ 1 ) n · 1 Аналогично найдём, что Мы говорили выше, что сопряжённые числа возникают часто как корни квадратного уравнения с целыми коэффициентами. В связи с последней задачей возникает такое желание: 9. Написать уравнение с целыми коэффициентами, один из корней которого равен после преобразований получаем Именно такое уравнение получилось бы в качестве характеристического, если бы мы применили упомянутую мелким шрифтом в конце предыдущего раздела общую теорию к исследованию линейного преобразования в предыдущей задаче. Заметим, кроме того, что мы на самом деле получили уравнение наименьшей степени (с целыми коэффициентами) с корнем Попробуйте это доказать! Мы разобрали несколько примеров, в которых затрагивались пограничные вопросы алгебры, математического анализа и теории чисел. (Каждому направлению, которое мы наметили, можно было бы посвятить более подробную статью в «Кванте»!) В заключение покажем ещё, как можно смотреть на основных героев статьи — «сопряжённые числа» — с чисто алгебраической точки зрения. и их «взаимодействие» устроено так же, как во множестве самосовмещений прямоугольника. Мы закончим эту статью набором задач, в основном продолжающих уже затронутые темы, но требующих иногда и новых соображений, и обещанным списком литературы. Что больше: или 2. √ 2 = 1 + 1 . 2 + 1 √ 2 + 1 Докажите, что уравнения имеют бесконечное множество решений в целых числах. 6. 7. 8. 9. = β 1/2 n + β –1/2 n . 12. 13. 14. 2 √ ( A 2 > B > 0, A > 0). 15.