Что такое перпендикулярные векторы
Перпендикулярность векторов
Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.
Координаты вектора на плоскости, равного по модулю и перпендикулярного данному
Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.
Алгоритм получения координат перпендикулярных векторов
Вектор на плоскости xOy, перпендикулярный данному вектору получают так:
Графический пример
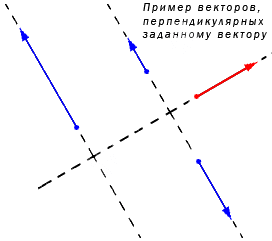
Рассмотрим небольшой графический пример (рис. 1).
На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: \(\vec\) и \(\vec\).
Векторы, изображенные черным цветом, перпендикулярны красному вектору.
Условие перпендикулярности векторов
Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.
Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.
Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.
Запишем условие перпендикулярности векторов.
Для двумерного случая:
\[ \large \boxed < a_
Для трехмерного случая:
\[ \large \boxed < a_
Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.
При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.
Примечание:
Есть такое правило: Количество неизвестных должно равняться количеству уравнений.
Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.
Перпендикулярные векторы в физике
В физике перпендикулярность некоторых векторов достаточно важна.
Вот несколько примеров:
Нахождение вектора, перпендикулярного данному вектору, примеры и решения
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Вторая часть доказательства
Условие перпендикулярности на координатной плоскости
Применим на практике и рассмотрим на примерах.
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Рассмотрим доказательство на примере.
Нахождение координат вектора, перпендикулярного двум заданным векторам
При решении применяется понятие векторного произведения векторов.
Разберем подробнее векторное произведение на примере задачи.
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
Как доказать что векторы перпендикулярны
Ключевые слова:
перпендикулярность, прямая линия, параллельность, вектор, коллинеарные вектора, координаты
Условие перпендикулярности векторов
Условие коллинеарности векторов
См. также:
Углы на плоскости, Координаты вектора
Напомним определение перпендикулярных векторов на плоскости и в трехмерном пространстве.
Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( 
радиан).
Для перпендикулярности двух ненулевых векторов 
и 
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство 
.
Пусть векторы 
и 
перпендикулярны. Докажем выполнение равенства 
.
По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы и перпендикулярны, то угол между ними равен девяноста градусам, следовательно, 
, что и требовалось доказать.
Переходим ко второй части доказательства.
Теперь считаем, что 
. Докажем, что векторы 
и 
перпендикулярны.
Так как векторы и ненулевые, то из равенства 
следует, что 
. Таким образом, косинус угла между векторами и равен нулю, следовательно, угол 
равен 
, что указывает на перпендикулярность векторов и .
Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.
Как же выглядит условие перпендикулярности двух векторов в координатной форме?
В разделе скалярное произведение в координатах мы показали, что для двух векторов с заданными координатами 
и 
на плоскости справедливо равенство 
, а для двух векторов 
и 
в пространстве 
. Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид 
на плоскости, а в трехмерном пространстве 
.
Рассмотрим применение полученных условий на практике, для этого разберем решение нескольких примеров.
Перпендикулярны ли векторы 
.
Вычислим их скалярное произведение по координатам 
. Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.
да, векторы перпендикулярны.
Перпендикулярны ли векторы 
и 
, где 
– координатные векторы прямоугольной системы координат в трехмерном пространстве.
Векторы 
и 
имеют соответственно координаты 
и 
(при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов: 
Так как 
, то векторы 
и 
не перпендикулярны.
нет, не перпендикулярны.
Найдите значение 
, при котором векторы 
и 
перпендикулярны.
Воспользуемся условием перпендикулярности двух векторов в пространстве в координатной форме 
векторы перпендикулярны при 
.
В некоторых случаях возможно ответить на вопрос о перпендикулярности двух векторов без использования необходимого и достаточного условия перпендикулярности. Например, когда известны длины всех сторон треугольника, построенного на двух векторах, то можно найти угол между векторами и посмотреть, равен ли он девяноста градусам.
Стороны АВ, АС и ВС треугольника АВС равны соответственно 8, 6 и 10 см. Убедитесь, что векторы 
и 
перпендикулярны.
Если векторы и перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство 
. Проверим его справедливость: 
.
Следовательно, АВ и АС – катеты прямоугольного треугольника АВС, поэтому, векторы и перпендикулярны.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 – 
| 7538 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов. Тема применима для задач, связанных с уравнениями прямых и плоскостей.
Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.
Необходимое и достаточное условие перпендикулярности двух векторов
Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.
При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.
Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?
Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.
Большинство случаев доказательства перпендикулярности двух ненулевых векторов на плоскости или в пространстве производится с помощью необходимого и достаточного условия перпендикулярности двух векторов.
Вторая часть доказательства
Условие перпендикулярности на координатной плоскости
Применим на практике и рассмотрим на примерах.
Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.
Ответ: да, заданные векторы a → и b → перпендикулярны.
Ответ: нет, векторы i → – j → и i → + 2 · j → + 2 · k → не перпендикулярны.
Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим
a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( – 2 ) · 1 = 0 ⇔ λ = 2
Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.
Нахождение вектора, перпендикулярного данному
Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.
Нахождение вектора, перпендикулярного данному в плоскости.
Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.
Рассмотрим доказательство на примере.
Нахождение координат вектора, перпендикулярного двум заданным векторам
При решении применяется понятие векторного произведения векторов.
Разберем подробнее векторное произведение на примере задачи.
Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :
a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 – k → · 1 · 0 – j → · 2 · 3 – i → · 0 · 2 = 3 · i → + ( – 6 ) · j → + 4 · k →
Перпендикулярные векторы
Другими словами, два вектора будут перпендикулярны, когда они образуют прямой угол, и поэтому их векторное произведение будет равно нулю.
Чтобы вычислить, перпендикулярен ли один вектор другому, мы можем использовать формулу для скалярного произведения с геометрической точки зрения. То есть с учетом того, что косинус образующего ими угла будет равен нулю. Следовательно, чтобы узнать, какой вектор перпендикулярен другому, нам нужно только установить векторное произведение равным 0 и найти координаты таинственного перпендикулярного вектора.
Формула двух перпендикулярных векторов
Основная идея перпендикулярности двух векторов заключается в том, что их векторное произведение равно 0.
Учитывая, что для любых двух перпендикулярных векторов их векторное произведение будет:
Выражение гласит: «вектор к перпендикулярно вектору б”.
Мы можем выразить приведенную выше формулу в координатах:
График двух перпендикулярных векторов
Предыдущие векторы, представленные на плоскости, будут иметь следующую форму:
Где мы можем извлечь следующую информацию:
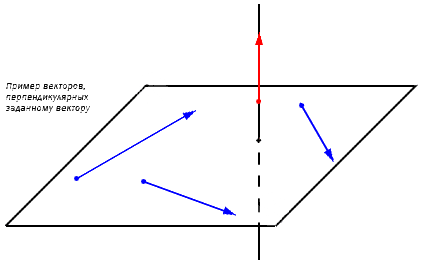
Вектор, перпендикулярный плоскости, известен как вектор нормали и обозначается значком п, такое, что:
Демонстрация
Мы можем доказать условие, что произведение двух перпендикулярных векторов равно нулю, за несколько шагов. Следовательно, нам нужно запомнить формулу векторного произведения только с геометрической точки зрения.
2. Мы знаем, что два перпендикулярных вектора образуют угол в 90 градусов. Итак, альфа = 90, так что:
3. Затем мы вычисляем косинус 90:
4. Мы видим, что при умножении косинуса 90 на произведение модулей все удаляется, потому что они умножаются на 0.
5. Наконец, условие будет:
Пример
Выразите уравнение через любой вектор, перпендикулярный вектору v.
Для этого определим вектор п any, и мы оставляем их координаты неизвестными, поскольку мы их знаем.
Итак, применяем формулу векторного произведения:
Наконец, выразим векторное произведение в координатах:
Решаем предыдущее уравнение:
Итак, это будет уравнение как функция вектора п который был бы перпендикулярен вектору v.