Что такое плоская поверхность
Разновидности плоских поверхностей
Плоские поверхности на чертеже
Совокупность элементов моделирования поверхности, обеспечивающая закон её образования, называют определителем поверхности. Например, записывают: плоскость 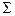
Все поверхности (геометрические фигуры) условно разделяют на два вида: плоские и кривые.
В этом разделе рассмотрим плоские поверхности.
Различают плоские поверхности простые и составные.
Простые плоские поверхности бывают двух видов: плоскости и грани.
задают изображением элементов определителя.
Плоскость моделируют как траекторию непрерывного перемещения прямой образующей (прямолинейного или вращательного вокруг оси, перпендикулярной образующей прямой).
Перемещение образующей можно задавать следующим образом.
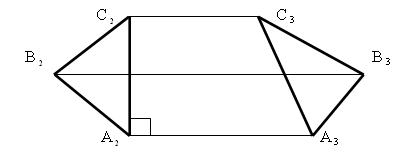
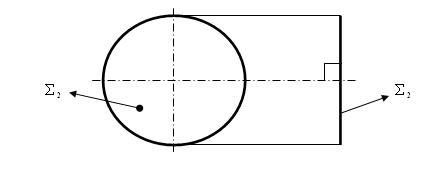
На рис. 5.1 – 5.3 представлены изображения граней: треугольника, четырёхугольника и круга.
Составные плоские поверхности (многогранные) – представляют собой несколько граней (не лежащих в одной плоскости), состыкованных между собой. Линию стыка каждой пары граней называют рёбром, которое является общей линией границ этих граней (их общей образующей).
Составные плоские поверхности подразделяют на монотипные и комплексные многогранные поверхности.
Монотипные многогранные поверхности моделируют с помощью направляющей ломаной прямой линии. При этом различают следующие варианты таких поверхностей.
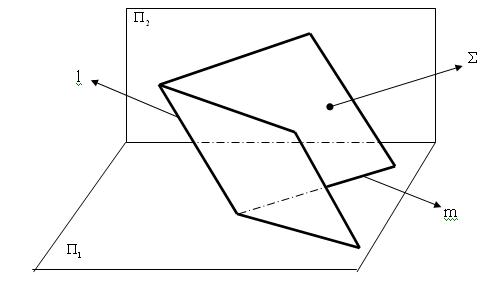
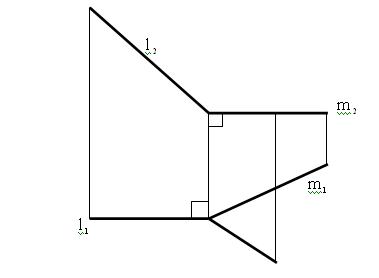
Призматическая поверхность. Моделирование призматической поверхности производят путём параллельного перемещения образующей прямой l по направляющей ломаной прямой m (все рёбра между собой параллельны).
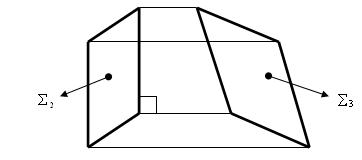
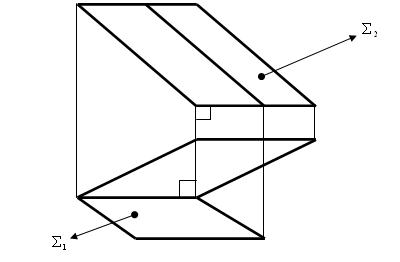
На рис. 5.4 представлен аксонометрический чертёж призматической поверхности.
Комплексный чертёж определителя призматической поверхности представлен на рис. 5.5.
Комплексный чертёж призматической поверхности выполнен на рис. 5.6.
Частным случаем призматической поверхности является призма, которая представляет собой замкнутую призматическую поверхность (направляющая ломаная прямая – замкнута).
На рис. 5.7 приведён чертёж прямой трёхгранной призмы.
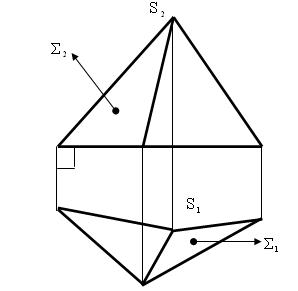
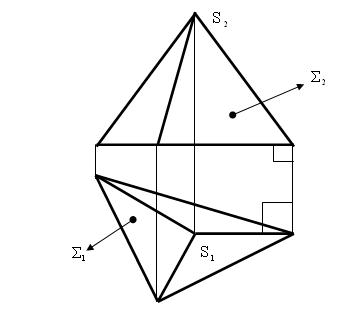
На рис. 5.8 представлен комплексный чертёж пирамидальной поверхности.
Частным случаем пирамидальной поверхности является пирамида, которая представляет собой замкнутую пирамидальную поверхность (направляющая ломаная прямая – замкнута).
На рис. 5.9 представлен комплексный чертёж трёхгранной пирамиды.
Комплексные многогранные поверхности получают стыковкой многогранных поверхностей и граней разного типа.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Что такое плоская поверхность
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке познакомимся с плоскими поверхностями, узнаем, что такое плоскость.
На альбомном листе нужно что-то нарисовать.
В комнате стоят мягкое кресло, журнальный столик и диван.
На какой из этих предметов положим альбомный лист?
Конечно на журнальный стол, так как у него поверхность плоская.
У дивана и кресла поверхность искривленная, поэтому положив на них лист бумаги, рисовать будет неудобно.
В безветренную погоду плоской будет поверхность озера, а при ветре станет искривленной. Плоской можно назвать поверхность пола, потолка и стены, листа бумаги и оконного стекла.
Выполним практическую работу:
На листе бумаги построим с помощью циркуля круг с радиусом 4 см.
Увеличим радиус в 2 раза и начертим круг с этим же центром.
Увеличим еще в 2 раза радиус и начертим третий круг с тем же центром.
Если этот процесс продолжить, то постепенно круги заполнят весь лист бумаги.
Этот процесс может быть бесконечным, какую бы точку плоскости мы не выбрали.
Такая же ситуация сложится, если вместо круга возьмем другую фигуру, например, квадрат, треугольник и т.п.
Лист бумаги может «продолжаться» на листе ватмана, лист ватмана «продолжается» на школьной доске, школьная доска «продолжается» на стене.
Итак, плоскость похожа на лист бумаги или спокойную поверхность озера, которые могут продолжаться бесконечно.
Круг, треугольник, квадрат, прямоугольник – плоские фигуры.
Любая из этих фигур – часть плоскости.
Чтобы выделить эту часть плоскости нужно закрасить фигуру.
Геометрическая фигура перестанет быть плоской, если ее изогнуть.
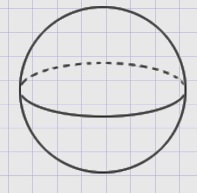
Куб, цилиндр, шар, конус – это объемные предметы, их в математике называют геометрическими телами.
Поверхность грани куба, основания цилиндра и конуса – плоские.
Тень объемных предметов – плоская.
С помощью солнечного света можно получить плоское изображение реального предмета. Однако по виду тени не всегда можно восстановить оригинал.
Например, форму круга может иметь тень мяча, колеса, тарелки.
Если взять куб и обвести его основание, то получится на листе квадрат – плоская фигура, в результате мы изобразили только одну грань куба. По такому изображению сложно разузнать куб, но как условное обозначение оно может использоваться на картах и схемах.
Чтобы на плоском листе бумаги изобразить объемный предмет, нужно применять правила рисования объемных предметов на плоскости, с помощью которых нарисованный на плоскости предмет кажется объемным.
Такое изображение в математике называется наглядным.
Для наглядного изображения куба достаточно показать три его грани. Для наглядного изображения мяча нужно провести дополнительные линии.
Итак, на этом уроке мы рассмотрели «плоские поверхности», познакомились с понятием «плоскость», а также убедились в возможности изображения на плоскости объемных предметов.
«Плоские поверхности. Плоскость»
Цели: ввести понятие «плоскость»; учить сравнивать и приводить примеры плоской поверхности и искривленной; совершенствовать умение изображать геометрические фигуры; развивать пространственное мышление.
Содержимое разработки
«Плоские поверхности. Плоскость«
cформировать представления о плоской поверхности и плоскости
работать над усвоением правила порядка действий в выражениях
Над умением выполнять поставленные задачи
развивать логическое мышление, умение анализировать
Развивать умение работать в парах
Учить слушать ответы других
Оборудование: учебник для второго класса Л.Г. Петерсон “Математика” 2 часть; геометрические фигуры и тела: прямоугольник, квадрат, треугольник, круг, цилиндр, куб, пирамида, конус, параллелепипед, шар; карточки с изображением геометрических тел: цилиндр, куб, пирамида, конус, параллелепипед, шар; листы бумаги и фломастеры.
Орг. момент (1 минута)
Математику нельзя изучать наблюдая, как это делает сосед.
Дети читают и поясняют высказывание
2. Актуализация знаний
— Рассмотрите запись, что можете сказать?
— На какие группы можно разделить выражения?
— Прочитайте по-разному буквенные выражения.
— Прочитать числовые выражения
Составь выражения и найди значения: с.34 №7
Ребята показывают ответы на дощечках
3Постановка цели урока
— Посмотрите на доску и скажите, с чем мы будем работать сегодня на уроке?
На доске расположены геометрические фигуры: треугольник, круг, квадрат, прямоугольник. Все фигуры сделаны из картона одного цвета. Поверхность треугольника сделана специально неровная, с бугорками.
— С геометрическими фигурами.
— Что это за фигуры, как они называются?
— Это квадрат, треугольник, круг, прямоугольник.
— Они одного цвета. Изготовлены из одного материала.
— А есть ли среди них лишняя фигура? Почему она лишняя?
— Да. Круг, у него нет углов.
— Треугольник, у него поверхность отличается от других фигур.
— Мне нужен один помощник, чтобы исследовать данные фигуры.
Один ученик выходит к доске.
— Потрогай, погладь поверхность лишней фигуры – треугольника.
— Поверхность неровная, негладкая, на ней есть ямки и бугорочки.
— А теперь исследуй поверхность оставшихся фигур. Какая у них поверхность?
— У других фигур поверхность гладкая, ровная.
— А ещё такую поверхность называют плоской.
— Что значит плоский, как вы понимаете?
-Перед вами несколько предметов: Стул, тетрадь. Полка. Чем они похожи?
Все эти предметы имеют ровную поверхность
-Какие еще предметы имеют плоские поверхности?
Доска, стена стол и др.
— Плоский – значит ровный, без возвышений и углублений, с прямой и гладкой поверхностью.
4. Постановка учебной задачи (4-5 минут)
— Ребята, как вы думаете, я случайно попросила вас обратить внимание на поверхность фигур?
— Будем работать над поверхностями фигур.
— Попробуйте сформулировать тему сегодняшнего урока.
Учитель на доске открывает часть темы урока: “Плоские поверхности”.
“Открытие” детьми нового знания (7-8 минут)
— У меня на столе стоят геометрические тела.
— Кто может назвать эти тела?
Учитель показывает тела: цилиндр, куб, конус, параллелепипед, пирамида, шар.
— Это цилиндр, куб, конус, параллелепипед, пирамида, шар.
— Ребята, как вы думаете, а у этих геометрических тел есть плоские поверхности? Докажите.
Мне нужен помощник.
— Есть. Если провести рукой по поверхности, она будет ровной и гладкой.
— Я с вами согласна. И предлагаю выполнить задание.
У вас на листочках нарисовано геометрическое тело, вы должны синим карандашом заштриховать плоские поверхности данного тела.
Дети выполняют задание по вариантам. Один представитель каждого варианта выходит к доске и выполняет своё задание на доске.
На доске изображены геометрические тела: цилиндр, куб, конус, параллелепипед, пирамида, шар.
— При выполнении этого задания у вас возникли трудности. Давайте попробуем разрешить их.
— С какими геометрическими телами были затруднения? Почему?
— С цилиндром, конусом и шаром. Затруднялись, не могли найти плоские поверхности.
— А у каких тел легко определили плоские поверхности?
— Давайте понаблюдаем, возьмём в руки куб, проведём по одной плоской поверхности, по другой плоской поверхности. Что есть у этих поверхностей?
— Проведите рукой по поверхности шара. Что заметили, есть у этого тела край?
— Значит, какой можно сделать вывод из наших наблюдений?
-Если же представить, что плоскую поверхность можно продолжить во всех направлениях так, чтобы у нее не было краев, то в таком случае мы получили плоскость. Плоскость не имеет краев, продолжается во всех направлениях без конца и края.
— А сейчас закройте глаза и представьте море. Безветренная погода, море спокойно, на нем нет ни единой волны. Море простирается без конца и края, так, что мы не видим берегов. Плоскость- это как поверхность моря, когда не видно берегов.
— У плоских поверхностей есть края
Звук волн. Релаксация..
— Как проверить правильность наших рассуждений?
— Откроем учебник на странице 35 и прочитаем сведения в жёлтой рамочке.
— Плоские поверхности имеют края. У плоскости края нет. Её можно продолжить во всех направлениях.
— Помогут новые сведения решить проблемы, которые у нас возникли?
(Учитель вместе с детьми разбирают трудности, которые возникли при работе с цилиндром, конусом, шаром.)
— Итак, ребята, что нового мы узнали сегодня на уроке математики?
— Что плоские поверхности – это поверхности гладкие, ровные без возвышений и углублений. У плоских поверхностей есть края, а у плоскости краёв нет. Плоскость можно продолжить во всех направлениях.
— Ребята, можем мы дополнить тему нашего урока: “Плоские поверхности. Плоскость”?
— Приведите примеры плоских поверхностей из окружающей обстановки.
— Столешница у стола, учебник, доска, пол в классе.
— А привести примеры плоскости вы можете?
— Нет. В природе плоскости не существует.
6. Первичное закрепление (4-5 минут)
— Вопросы есть по новому материалу ко мне, друг другу?
— Выполняем задание №3, страница 35. Прочитайте задание про себя. Скажите, что нужно сделать в задании?
— Нужно провести две пересекающиеся прямые, которые проходят через точку О. Определить, на сколько частей эти прямые разделили плоскость и раскрасить эти части в разные цвета.
— Выполняем задание №3 в учебнике по этапам с комментарием.
1. Проводим через точку О прямую.
2. Проводим вторую прямую, которая пересекает первую прямую в точке О.
3. Две пересекающиеся прямые делят плоскость на 4 части.
4. Раскрашиваем каждую часть разными цветами.
— Итак, сегодня на уроке математики мы познакомились с новым материалом. Интересно было?
— С этим материалом мы будем работать на следующих уроках.
7. Физ. минутка (1-2 минуты)
— Ребята, сегодня на уроке математики мы должны с вами решить задачу и поработать с выражением. Чем вы хотите заняться в первую очередь?
— На последних уроках математики мы с вами решали задачи, находили значения выражений используя алгоритм.
— Кто помнит, какие виды алгоритмов бывают?
— Линейные, разветвляющиеся и циклические.
— Это линейный алгоритм, т.к. все действия идут подряд.
Один ученик решает задачу на доске, остальные ребята решают в тетрадях.
— Проверяем. Объясни, как нашёл задуманное число? Какими знаниями пользовался?
— Я находил неизвестное число с помощью уравнения. Чтобы найти задуманное число, нужно выполнить обратные операции.
— Учитель проверяет и ставит + тем, кто решил правильно
— Кто сделал задание на все “+”? Молодцы!
Дети поднимают руки.
— Прочитайте и скажите, о чем говорится в задаче?
Что сделали с цветами? Прочитайте вопрос задачи. Что нужно найти?
Что обозначает весь отрезок?
О том что дети собирали ромашки колокольчики.
Поставили в 2 вазы.
Все цветы, которые собрали на поляне.
Решить задачу самостоятельно
Один ученик решает на закрытой доске
9. Рефлексия деятельности (2-3 минуты)
— Урок подходит к концу. Вам было интересно на уроке математики? Почему?
— Да. Мы интересно работали с геометрическими телами. Решали задачу и находили значение выражения.
— Что вы считаете нужным запомнить?
— Что такое плоская поверхность, чем она отличается от плоскости. Что не все геометрические тела имеют плоские поверхности.
— А эти знания вам нужны в жизни?
— Да. Мы сможем на практике определять плоскость и плоские поверхности. Это интересно.
Что такое плоская поверхность
Основные понятия и определения
Поверхность как объект инженерного исследования может быть задана следующими основными способами: а) уравнением; б) каркасом; в) определи гелем; г) очерком.
Составлением уравнений поверхностей занимается аналитическая геометрия; она рассматривает поверхность как множество точек, координаты которых удовлетворяют уравнению вида F (х,у, z) = 0.
В начертательной геометрии поверхность на чертеже задается каркасом, определителем, очерком.
Поверхность, образованная движущейся в пространстве линией, на чертеже может быть задана определителем поверхности.
Определителем поверхности называется совокупность геометрических фигур и связей между ними. позволяющих однозначно образовать поверхность в пространстве и задать ее на чертеже.
Способ образования поверхности движущейся в просфанстве линией называют кинематическим.
Линию, образующую при своем движении в пространстве данную поверхность называют образующей (производящей).
Образующая при своем движении может изменять свою форму или оставаться неизменной. Закон перемещения образующей можно, в частности, задать неподвижными линиями, на которые при своем движении опирается образующая. Эти линии называются направляющими.
На чертеже при задании поверхности ее определителем строятся проекции направляющих линий, указывается, как находятся проекции образующей линии. Построив ряд положений образующей линии, получим каркас поверхности. Пример образования поверхности кинематическим способом показан на рис. 96.
В качестве образующей а этой поверхности взята плоская кривая. Закон перемещения образующей задан двумя направляющими m и n и плоскостью а. Образующая а скользит по направляющим, все время оставаясь параллельной плоскости a.
Определитель поверхности выявляется путем анализа способов образования поверхности или се основных свойств. В общем случае одна и та же поверхность может быть образована несколькими способами, поэтому может иметь несколько определителей. Обычно из всех способов образования поверхности выбирают простейший. Например, боковая поверхность прямого кругового цилиндра может быть образована четырьмя способами (рис. 97):
а) как след, оставляемый в пространстве прямой а при ее вращении вокруг оси m (рис. 97,а).
б) как след, оставляемый в пространстве кривой линией b при ее вращении вокруг оси m (рис. 97,6).
в) как след, оставляемый в пространстве окружностью с при поступательном перемещении ее центра О вдоль оси m. при этом плоскость окружности все время остается перпендикулярной к этой оси (рис. 97,в).
г) как огибающую всех положений сферической поверхности р постоянного радиуса, центр которой перемещается по оси m (рис.97,г).
Наиболее простым из рассматриваемых будет определитель Ф ( а,m ) [ A1].
Задание поверхности на чертеже каркасом или определителем не всегда обеспечивает наглядность ее изображения. В некоторых случаях поверхность целесообразнее задавать ее очерком.
Очерком поверхности называется проекция проецирующей цилиндрической поверхности, огибающей заданную поверхность.
По известному уравнению поверхности или се определителю, или очерку всегда можно построить каркас поверхности.
Многообразие поверхностей требует их систематизации. Для поверхностей, образованных кинематическим способом в основу систематизации положен их определитель.
В зависимости от вида образующей поверхности разделяются на два класса:
Поверхности нелинейчатые
Поверхности нелинейчатые подразделяют на поверхности с образующей переменного вида (изменяющей свою форму в процессе движения) и на поверхности с образующей постоянного вида.
Нелинейчатые поверхности с образующей переменного вида
К нелинейчатым поверхностям с образующей переменного вида относятся:
1. Поверхность общего вида. Такая поверхность образуется перемещением образующей переменного вида а по криволинейной направляющей т (рис. 98).
2. Каналовая поверхность. Эта поверхность образуется движением плоской замкнутой линии, плоскость которой определенным образом ориентирована в пространстве (рис. 99).
Площадь, ограниченная образующей, монотонно изменяется в процессе ее движения но направляющей. Например, каналовую поверхность имеет переходный участок, соединяющий два трубопровода разной формы.
Примером циклической поверхности может быть корпус духового музыкального инструмента.
Нелинейчатые поверхности с образующей постоянного вида
К нелинейчатым поверхностям с образующей постоянного вида относятся:
1. Поверхность общего вида. Такая поверхность может быть образована движением произвольной кривой линии а по направляющей m (рис. 101).
2. Трубчатая поверхность. Образующей трубчатой поверхности является окружность постоянного радиуса. Плоскость окружности при ее движении остается перпендикулярной к направляющей (рис. 102).
Примером трубчатой поверхности может быть поверхность проволоки круглого сечения.
Поверхности линейчатые
Линейчатые поверхности образуются движением прямой (образующей) по заданному закону. В зависимости от закона движения образующей получаем различные линейчатые поверхности.
Линейчатые поверхности с тремя направляющими
К линейчатым поверхностям с тремя направляющими относятся:
1. Поверхность косого цилиндра. Такая поверхность может быть образована движением прямолинейной образующей по трем криволинейным направляющим (рис. 103).
P e ш е н и е. Для определения недостающей проекции точки, воспользуемся признаком принадлежности ее поверхности: точка принадлежит поверхности; если она принадлежит какой-либо линии этой поверхности.
Для данной линейчатой поверхности при построении проекций образующей сначала задается ее горизонтальная проекция, а затем находится фронтальная. Поэтому через известную горизонтальную проекцию точки A’ проводим проекцию образующей а’2, определяем ее фронтальную проекцию а2«, на которой по линии связи найдем искомую фронтальную проекцию точки A».
Для определения недостающей горизонтальной проекции точки В’ выполним следующие построения:
1. Построим ряд образующих заданной поверхности a1,a2,a3,a4 .
2. На фронтальной плоскости проекций через известную проекцию точки В» проведем проекцию вспомогательной линии b’ принадлежащей заданной поверхности и пересекающей образующие.
3. По известным фронтальным проекциям точек пересечения проекции линии b» с образующими а1«, а2«, а3«, а4« найдем горизонтальные проекции этих точек. Соединив их плавной линией, построим горизонтальную проекцию вспомогательной линии b’ на которой по линии связи найдем искомую проекцию точки В’.
К линейчатым поверхностям с тремя направляющими относятся, например, поверхности гребных винтов судов и пропеллеров самолетов. В архитектуре и строительстве они используются при возведении крытых зданий стадионов, рынков, вокзалов.
Линейчатые поверхности с двумя направляющими и плоскостью параллелизма (поверхности Каталана)
К линейчатым поверхностями с двумя направляющими плоскостью параллелизма относятся:
a( n ⊥ a) (рис. 108). Поверхность прямого коноида используется в гидротехническом строительстве для формирования поверхности устоев мостовых опор.
Линейчатые поверхности с одной направляющей (торсы)
1. Поверхность с ребром возврата. Эта поверхность образуется движением прямолинейной образующей, во всех своих положениях касательной к пространственной кривой, называемой ребром возврата.
2. Цилиндрическая поверхность. Данная поверхность образуется движением прямолинейной образующей, скользящей по кривой направляющей и остающейся параллельной своему исходному состоянию (рис.110).
3. Коническая поверхность. Эта поверхность образуется движением прямолинейной образующей, скользящей по кривой направляющей и проходящей во всех своих положениях через одну и ту же неподвижную точку S (рис. 111).