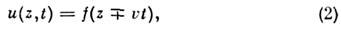Что такое плоская волна

ПЛОСКАЯ ВОЛНА

— волна, ук-рой направление распространения одинаково во всех точках пространства. = v _ф= v) существуют стационарные (т. е. перемещающиеся как целое) бегущиеП. в., к-рые можно представить в общем виде

Полезное

Смотреть что такое «ПЛОСКАЯ ВОЛНА» в других словарях:

плоская волна — Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны. [ГОСТ 24346 80] плоская волна 1. Волна с плоскими фронтами 2. Волна, в которой частицы с одной фазой лежат на плоских параллельных… … Справочник технического переводчика

плоская волна — Волны на поверхности океанов и морей, образующиеся из ветровых волн после полного прекращения воздействия на них ветра (обычно зыбь длиннее ветровых волн и более правильна). Syn.: зыбь … Словарь по географии

Плоская волна — 71. Плоская волна Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

плоская волна — plokščioji banga statusas T sritis fizika atitikmenys: angl. plane wave vok. ebene Welle, f; flache Welle, f rus. плоская волна, f pranc. onde plane, f … Fizikos terminų žodynas

Плоская волна — волна, в которой всем точкам, лежащим в любой плоскости, перпендикулярной к направлению её распространения, в каждый момент соответствуют одинаковые смещения и скорости частиц среды (для механических волн) или одинаковые напряжённости… … Большая советская энциклопедия

ортогонализированная плоская волна — ortogonalizuotoji plokščioji banga statusas T sritis fizika atitikmenys: angl. orthogonalized plane wave vok. orthogonalisierte ebene Welle, f rus. ортогонализированная плоская волна, f pranc. onde plane orthogonalisée, f … Fizikos terminų žodynas

плоская радиоволна — плоская волна Поперечная радиоволна, поверхности равных фаз которой представляют собой параллельные плоскости, перпендикулярные к направлению распространения. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины распространение радиоволн… … Справочник технического переводчика

Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия

Плоская радиоволна — 46. Плоская радиоволна Плоская волна Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

плоская световая волна — Световая волна, фронт которой представляет собой плоскость. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика Обобщающие термины… … Справочник технического переводчика

Источник

Плоская волна

Смотреть что такое «Плоская волна» в других словарях:

ПЛОСКАЯ ВОЛНА — волна, у к рой направление распространения одинаково во всех точках пространства. Простейший пример однородная монохроматич. незатухающая П. в.: и(z, t)=Aeiwt±ikz, (1) где А амплитуда, j= wt±kz фаза, w=2p/Т круговая частота, Т период колебаний, k … Физическая энциклопедия

плоская волна — Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны. [ГОСТ 24346 80] плоская волна 1. Волна с плоскими фронтами 2. Волна, в которой частицы с одной фазой лежат на плоских параллельных… … Справочник технического переводчика

плоская волна — Волны на поверхности океанов и морей, образующиеся из ветровых волн после полного прекращения воздействия на них ветра (обычно зыбь длиннее ветровых волн и более правильна). Syn.: зыбь … Словарь по географии

Плоская волна — 71. Плоская волна Волна, фронт которой представляет собой плоскость, перпендикулярную к направлению распространения волны Источник: ГОСТ 24346 80: Вибрация. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

плоская волна — plokščioji banga statusas T sritis fizika atitikmenys: angl. plane wave vok. ebene Welle, f; flache Welle, f rus. плоская волна, f pranc. onde plane, f … Fizikos terminų žodynas

ортогонализированная плоская волна — ortogonalizuotoji plokščioji banga statusas T sritis fizika atitikmenys: angl. orthogonalized plane wave vok. orthogonalisierte ebene Welle, f rus. ортогонализированная плоская волна, f pranc. onde plane orthogonalisée, f … Fizikos terminų žodynas

плоская радиоволна — плоская волна Поперечная радиоволна, поверхности равных фаз которой представляют собой параллельные плоскости, перпендикулярные к направлению распространения. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины распространение радиоволн… … Справочник технического переводчика

Волна — У этого термина существуют и другие значения, см. Волна (значения). Волна изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами,… … Википедия

Плоская радиоволна — 46. Плоская радиоволна Плоская волна Источник: ГОСТ 24375 80: Радиосвязь. Термины и определения оригинал документа … Словарь-справочник терминов нормативно-технической документации

плоская световая волна — Световая волна, фронт которой представляет собой плоскость. [Сборник рекомендуемых терминов. Выпуск 79. Физическая оптика. Академия наук СССР. Комитет научно технической терминологии. 1970 г.] Тематики физическая оптика Обобщающие термины… … Справочник технического переводчика

Источник

Плоская волна

Другими решениями волнового уравнения являются сферическая волна ( концентрическая вокруг точки) и цилиндрическая волна (концентрическая вокруг прямой линии). Их можно легко аппроксимировать на небольших участках вдали от центра с помощью плоской волны.

Содержание

Однородная гармоническая плоская волна

Плоскую волну проще всего описать, если выбрать систему координат так, чтобы одна ось соответствовала направлению ее распространения. В направлениях, перпендикулярных распространению, не происходит колебаний. Таким образом, гармоничную однородную плоскую волну можно назвать

представляет собой плоское уравнение для волнового фронта.

Общая форма плоской волны

В общих чертах плоская волна описывается формулой

Плоская волна является решением волнового уравнения

На практике используются только гармонические плоские волны, поскольку любую общую плоскую волну можно представить как сумму гармонических плоских волн. Это связано с тем, что общую форму плоской волны A можно представить в виде интеграла Фурье :

Неоднородная плоская волна

Плоская волна всегда является решением уравнения Гельмгольца (временное преобразование Фурье волнового уравнения)

Чтобы уравнение Гельмгольца оставалось верным, волновое число должно оставаться действительным, что связано с условием k → ⋅ k → знак равно k 2 ( ω ) <\ displaystyle <\ vec > \ cdot <\ vec > = k ^ <2>(\ omega)>

и означает ограничение на выбор комплексного волнового вектора. Это условие явно означает, что действительная часть ( ) волнового вектора должна быть перпендикулярна его мнимой части ( ). β → <\ displaystyle <\ vec <\ beta>>> α → <\ displaystyle <\ vec <\ alpha>>>

поглощение

Если действительная и мнимая части комплексного волнового вектора выбраны как параллельные векторы, мнимая часть волнового числа не равна нулю, как в предыдущем разделе, и волновое число становится комплексным.

Уровни постоянной фазы и постоянной амплитуды идентичны, только амплитуда экспоненциально убывает в направлении распространения. Итак, это однородная плоская волна.

идеализация

Плоская волна всегда заполняет бесконечно протяженное пространство и поэтому является идеализацией реальной волны. Потому что, с одной стороны, плоская волна не может быть излучена конечно протяженным передатчиком, а с другой стороны, энергия плоской волны бесконечна. Оба они нефизичны.

Источник

Что такое плоская волна

Уравнением волны называется выражение, которое дает смещение колеблющейся точки как функцию ее координат (x, y, z) и времени t.

Эта функция должна быть периодической как относительно времени, так и координат (волна – это распространяющееся колебание, следовательно периодически повторяющееся движение). Кроме того, точки, отстоящие друг от друга на расстоянии l, колеблются одинаковым образом.

Уравнение плоской волны

Найдем вид функции x в случае плоской волны, предполагая, что колебания носят гармонический характер.

Направим оси координат так, чтобы ось x совпадала с направлением распространения волны. Тогда волновая поверхность будет перпендикулярна оси x. Так как все точки волновой поверхности колеблются одинаково, смещение x будет зависеть только от х и t: . Пусть колебание точек, лежащих в плоскости , имеет вид (при начальной фазе )

Найдем вид колебания частиц в плоскости, соответствующей произвольному значению x. Чтобы пройти путь x, необходимо время .

Следовательно, колебания частиц в плоскости x будут отставать по времени на t от колебаний частиц в плоскости , т.е.

– это уравнение плоской волны.

Таким образом, x есть смещение любой из точек с координатой x в момент времени t. При выводе мы предполагали, что амплитуда колебания . Это будет, если энергия волны не поглощается средой.

Такой же вид уравнение (5.2.3) будет иметь, если колебания распространяются вдоль оси y или z.

В общем виде уравнение плоской волны записывается так:

Выражения (5.2.3) и (5.2.4) есть уравнения бегущей волны.

Уравнение (5.2.3) описывает волну, распространяющуюся в сторону увеличения x. Волна, распространяющаяся в противоположном направлении, имеет вид:

.

Уравнение волны можно записать и в другом виде.

Введем волновое число , или в векторной форме:

где – волновой вектор, – нормаль к волновой поверхности.

Так как , то . Отсюда . Тогда уравнение плоской волны запишется так:

Уравнение сферической волны

В случае, когда скорость волны υ во всех направлениях постоянна, а источник точечный, волна будет сферической.

Предположим, что фаза колебаний источника равна wt (т.е. ). Тогда точки, лежащие на волновой поверхности радиуса r, будут иметь фазу . Амплитуда колебаний здесь, даже если волна не поглощается средой, не будет постоянной, она убывает по закону . Следовательно, уравнение сферической волны:

где А равна амплитуде на расстоянии от источника равном единице.

Уравнение (5.2.7) неприменимо для малых r, т.к. при , амплитуда стремится к бесконечности. То, что амплитуда колебаний , следует из рассмотрения энергии, переносимой волной.

Источник

Бегущие электромагнитные волны

Уравнение плоской бегущей волны

Если волна движется по О х без поглощения энергии, то это характеризуется уравнением:

Что называют электромагнитной волной. Волновое число

Запись выражения ( 1 ) примет совершенно другой вид при известном волновом числе.

Если перейти к комплексным числам, применив формулу Эйлера, уравнение плоской волны зафиксируем.

Выражение ( 6 ) имеет физический смысл только в действительной части, но R e возможно опустить в записи уравнения волны.

Перейдем к рассмотрению волнового процесса, где не происходит изменение фазы.

При условии, что υ волны зависит от частоты колебаний, то такая волна подвержена дисперсии.

Уравнение сферической бегущей волны

Сферическая волна – это волна, волновая поверхность которой является концентрической сферой. Такое уравнение примет вид:

где r является расстоянием от центра волны до точки рассмотрения. Если имеем дело со сферической волной, то ее амплитуда колебаний не будет постоянной даже при условии, что энергия не поглощается средой. Ее убывание происходит обратно пропорционально расстоянию. Выполнение уравнения ( 8 ) возможно тогда, когда источник волн считается точечным.

Уравнение бегущей волны в любом виде подчинено волновому уравнению.

За основу необходимо принять выражение для амплитуд электромагнитной волны:

Для записи уравнения колебаний H → в электромагнитной волне, в случае если она считается плоской и распространяется по О х :

Необходимо учитывать, что тело, которое поглощает падающую на него энергию, оказывается под давлением, равным среднему значению объемной плотности энергии в электромагнитной волне.

Следует применять соотношение амплитуд электромагнитной волны, которое записывается:

Следует, что значение объемной плотности электрической энергии примет вид:

Формула плотности магнитного поля:

После усреднения плотности, имеем:

Источник