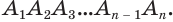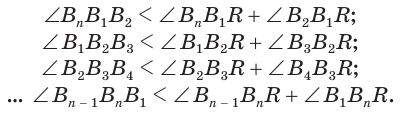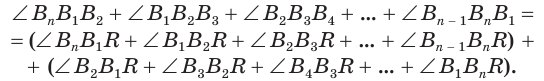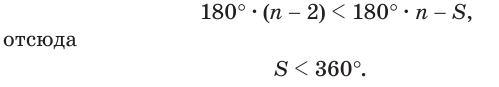Что такое плоские углы трехгранного угла
Трёхгранный угол
Трёхгранный угол — это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгранного угла. Стороны углов называются рёбрами, плоские углы при вершине трёхгранного угла называются его гранями. Каждая из трёх пар граней трёхгранного угла образует двугранный угол (ограниченных третьей гранью, не входящей в пару; при потребности естественным образом снимается это ограничение, в результате чего получаются необходимые полуплоскости, образующие весь двугранный угол без ограничения). Если поместить вершину трёхгранного угла в центр сферы, на её поверхности образуется ограниченный им сферический треугольник, стороны которого равны плоским углам трехгранного угла, а углы — его двугранным углам.
Содержание
Неравенство треугольника для трёхгранного угла
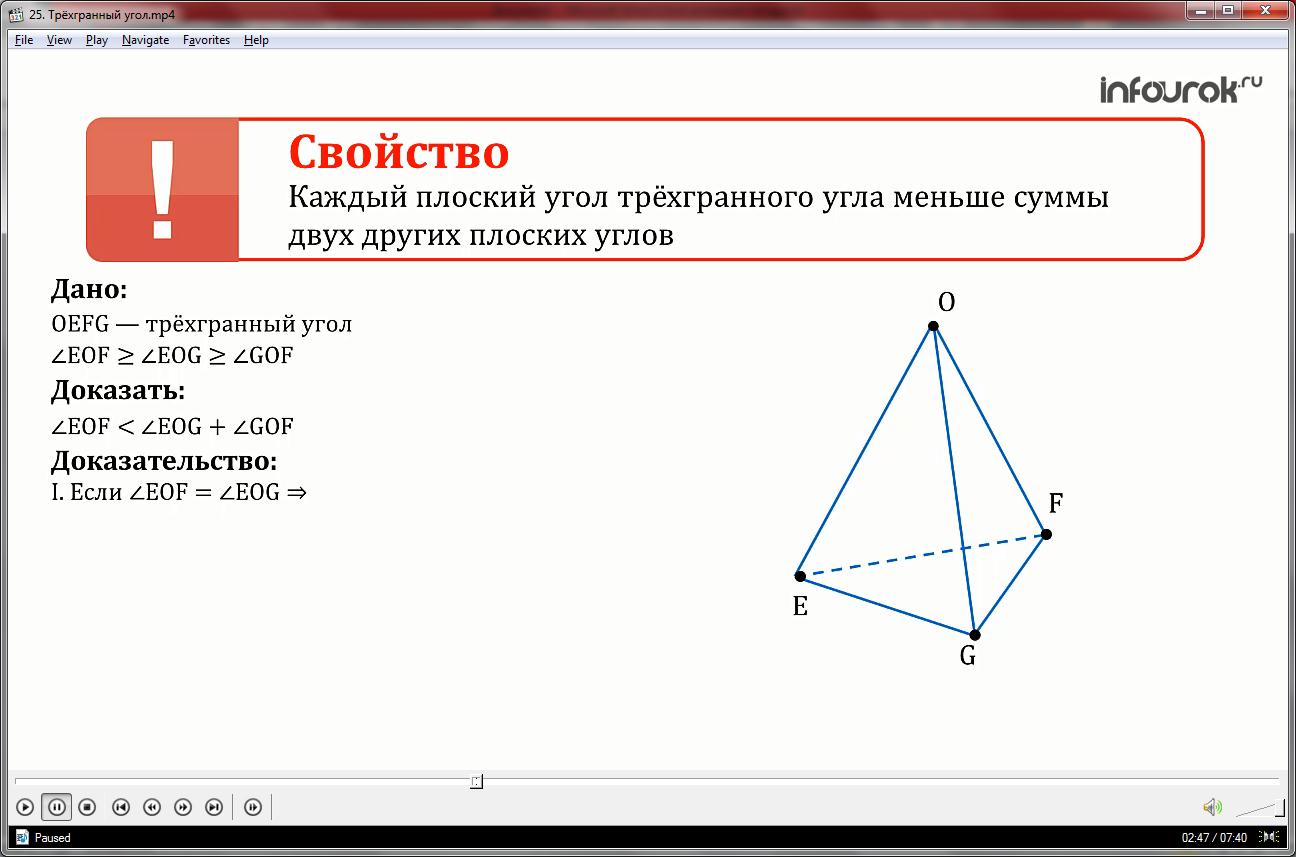
Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов.
Сумма плоских углов трёхгранного угла
Сумма плоских углов трёхгранного угла меньше 360 градусов.
Пусть OABC – данный трехгранный угол. Рассмотрим трехгранный угол с вершиной A, образованный гранями ABO, ACO и углом BAC. Напишем неравенство:
Аналогично, и для оставшихся трехгранных углов с вершинами B и С:
Складывая эти неравенства и учитывая, что сумма углов треугольника ABC равна 180°, получаем
Следовательно : 
Теорема косинусов для трёхгранного угла
Первая теорема косинусов для трехгранного угла 
Вторая теорема косинусов для трехгранного угла 
где α, β, γ — плоские углы, A, B, C — двугранные углы, составленные плоскостями углов β и γ, α и γ, α и β.
Напишем первую теорему косинусов для него
и после упрощений получаем:
Теорема синусов для трёхгранного угла
, где α, β, γ — плоские углы трёхгранного угла; A, B, C — противолежащие им двугранные углы.
См. также
Полезное
Смотреть что такое «Трёхгранный угол» в других словарях:
Трёхгранный угол — часть пространства, ограниченная бесконечной треугольной пирамидой (см. рис.). Грани этой пирамиды называются гранями Т. у., её вершина вершиной Т. у., полупрямые, по которым пересекаются грани, называются ребрами Т. у. Ребра образуют… … Большая советская энциклопедия
трёхгранный угол — Пространственная фигура, образованная тремя лучами, исходящими из одной точки и не лежащими в одной плоскости. [http://sl3d.ru/o slovare.html] Тематики машиностроение в целом … Справочник технического переводчика
трёхгранный угол — см. Телесный угол. * * * ТРЕХГРАННЫЙ УГОЛ ТРЕХГРАННЫЙ УГОЛ, см. Телесный угол (см. ТЕЛЕСНЫЙ УГОЛ) … Энциклопедический словарь
ТРЁХГРАННЫЙ УГОЛ — см. Телесный угол … Естествознание. Энциклопедический словарь
ТРЁХГРАННЫЙ — ТРЁХГРАННЫЙ, трёхгранная, трёхгранное. 1. Имеющий три грани. Трехгранная призма. 2. Образуемый пересечением трех граней, проходящих через одну точку (мат.). Трёхгранный угол. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
Трехгранный угол — Трёхгранный угол это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгранного угла. Стороны углов называются… … Википедия
телесный угол — часть пространства, ограниченная некоторой конической поверхностью (рис. 1); в частности, трёхгранный (рис. 2) и многогранный (рис. 3) углы ограничены соответственно тремя и многими плоскими гранями, сходящимися в вершине телесного угла. Единицу… … Энциклопедический словарь
ТЕЛЕСНЫЙ УГОЛ — часть пространства, ограниченная нек рой конич. поверхностью (рис. 1); в частности, трёхгранный (рис. 2) и многогранный (рис. 3) углы ограничены соотв. тремя и мн. плоскими гранями, сходящимися в вершине Т. у. Значение Т. у. равно отношению… … Естествознание. Энциклопедический словарь
трёхгранный — ая, ое. 1) Имеющий три грани. Трёхгра/нный напильник. Т ые штыки. 2) матем. Образуемый пересечением трёх граней, проходящих через одну точку. Трёхгра/нный угол … Словарь многих выражений
Сферическая теорема Пифагора — Прямоугольный сферический треугольник с гипотенузой c, катетами a и b и прямым углом C. Сферическая теорема Пифагора теорема, устанавливающая соотношение между сторонами прямоугольного … Википедия
Урок «Трёхгранный угол»
Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Для изучения сегодняшней темы нам необходимо вспомнить:
1) неравенство треугольника: каждая сторона треугольника меньше суммы двух других сторон.
2) теорему о соотношении сторон и углов треугольника: напротив большей стороны лежит больший угол.
3) свойство равнобедренного треугольника:
в равнобедренном треугольнике высота, проведенная к основанию, является медианной и высотой;
3) первый признак равенства треугольников: если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу
между ними другого треугольника, то такие треугольники равны.
Определение: Трехгранный угол – это часть пространства, ограниченная тремя углами с общей вершиной, не лежащих в одной плоскости и имеющими попарно общие стороны.
Общая вершина этих углов называется вершиной трехгранного угла. Стороны углов называются ребрами, углы, заключенные между парами лучей являются плоскими углами и называются гранями трехгранного угла. Грани трехгранного угла образуют двугранные углы.
Докажет свойство плоских углов трехгранного угла:
Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов.
Рассмотрим трехгранный угол OEFG, предположим, что EOF EOG GOF
Докажем случай EOF EOG.
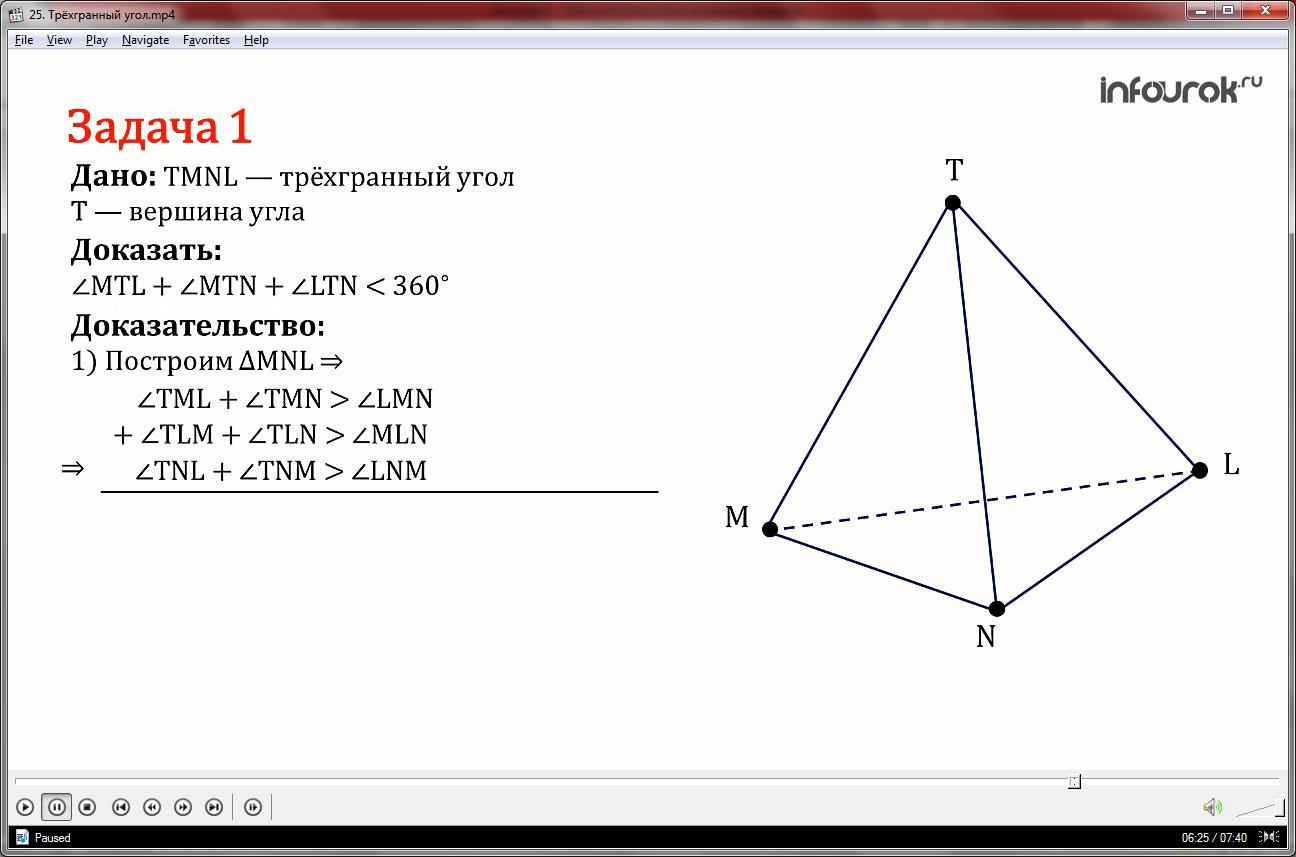
Поступим следующим образом на EF выберем точку S, где угол EOG равен углу EOS, а поскольку EOG LMN),
Далее мы складываем все неравенства, по частям, получаем одно неравенство, где в правой части, находятся углы треугольника MNL, а в левой сумма пар углов треугольников построенных на плоских углах трехгранного угла TMNL.
Используя свойство неравенства отнимает его обе части от положительного числа 540º, поменяв его знак на противоположный, в левой части число 540º представляем в виде суммы трех числе 180º и сгруппировав их,
Получаем неравенство, где в левой части сумма плоских углов трехгранного угла TMNL
Применив теорему о сумме углов треугольника, получаем неравенство
© 2021 Проект «Уроки математики»
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.
Трехгранный угол
Трехгранный угол
Трёхгранный угол — это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгранного угла. Стороны углов называются рёбрами, плоские углы при вершине трёхгранного угла называются его гранями. Грани трёхгранного угла образуют двугранные углы.
Неравенство треугольника для трёхгранного угла
Каждый плоский угол трёхгранного угла меньше суммы двух других его плоских углов.
Теорема косинусов для трёхгранного угла
cosα = cosβcosγ + sinβsinγcosA, где α, β, γ — плоские углы, A — двугранный угол, составленный плоскостями углов β и γ.
Теорема синусов для трёхгранного угла
, где α, β, γ — плоские углы трёхгранного угла; A, B, C — противолежащие им двугранные углы.
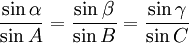
Полезное
Смотреть что такое «Трехгранный угол» в других словарях:
ТРЕХГРАННЫЙ УГОЛ — см. Телесный угол … Большой Энциклопедический словарь
трехгранный — ТРЁХГРАННЫЙ ая, ое. 1. Имеющий три грани. Т. напильник. Т ые штыки. 2. Матем. Образуемый пересечением трёх граней, проходящих через одну точку. Т. угол … Энциклопедический словарь
Трёхгранный угол — Трехгранный угол. Трёхгранный угол это часть пространства, ограниченная тремя плоскими углами с общей вершиной и попарно общими сторонами, не лежащими в одной плоскости. Общая вершина О этих углов называется вершиной трёхгран … Википедия
Телесный угол — Телесный угол часть пространства, которая является объединением всех лучей, выходящих из данной точки (вершины угла) и пересекающих некоторую поверхность (которая наз … Википедия
Двугранный угол — и линейный угол двугранного угла … Википедия
трёхгранный угол — см. Телесный угол. * * * ТРЕХГРАННЫЙ УГОЛ ТРЕХГРАННЫЙ УГОЛ, см. Телесный угол (см. ТЕЛЕСНЫЙ УГОЛ) … Энциклопедический словарь
ТЕЛЕСНЫЙ УГОЛ — часть пространства, ограниченная некоторой конической поверхностью, в частности трехгранный и многогранный углы ограничены соответственно тремя и многими плоскими гранями, сходящимися в вершине телесного угла. Единицу измерения телесного угла… … Большой Энциклопедический словарь
ТЕЛЕСНЫЙ УГОЛ — часть пространства, ограниченная некоторой конической поверхностью, в частности трехгранный и многогранный углы ограничены соответственно тремя и многими плоскими гранями, сходящимися в вершине телесного угла. Единицу измерения телесного угла… … Большой Энциклопедический словарь
телесный угол — часть пространства, ограниченная некоторой конической поверхностью (рис. 1); в частности, трёхгранный (рис. 2) и многогранный (рис. 3) углы ограничены соответственно тремя и многими плоскими гранями, сходящимися в вершине телесного угла. Единицу… … Энциклопедический словарь
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №12. Многогранные углы
Перечень вопросов, рассматриваемых в теме.
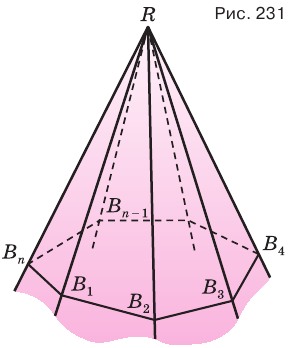
Три луча с общим началом в точке O — OA, OB и OC, которые не лежат в одной плоскости образуют трехгранный угол ОАВС.
Свойство трехгранного угла: каждый плоский угол трехгранного угла меньше сумму двух других плоских углов.
Утверждение: для любого выпуклого многогранного угла существует плоскость, пересекающая все его ребра.
Теорема: Сумма плоских углов выпуклого многогранного угла меньше 360°.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Рассмотрим три луча с общим началом в точке O — OA, OB и OC, которые не лежат в одной плоскости (рис. 1). Каждая пара лучей образует плоский угол. Три угла АОВ, ВОС, СОА образуют трехгранный угол ОАВС. Каждый из углов АОВ, ВОС, АОС является плоским углом этого трехгранного угла. Каждый плоский угол трехгранного угла меньше сумму двух других плоских углов.
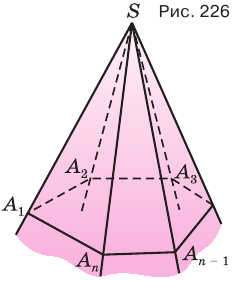
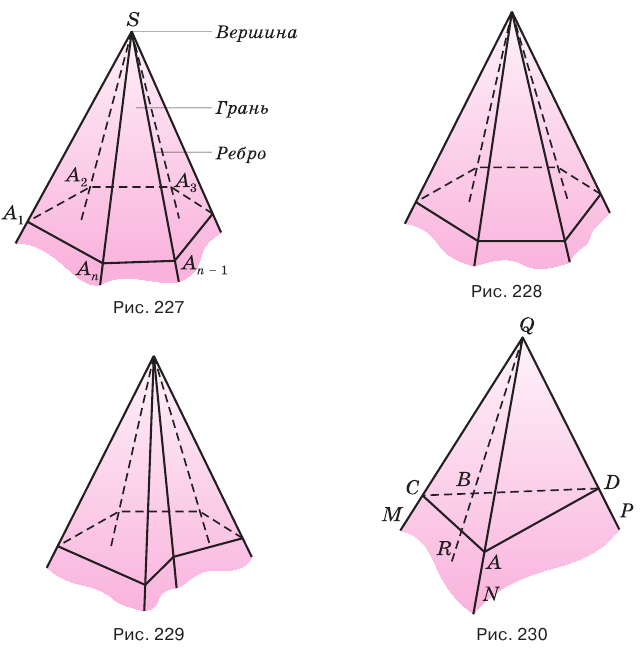
Рассмотрим фигуру, составленную из углов А1ОА2, А2ОА3, и так далее до АпОА1 и их внутренних областей так, что смежные углы не лежат в одной плоскости, а несмежные углы не имеют общих точек (рис. 2). Такая фигура называется многогранным углом. Такой угол называется выпуклым, если он лежит по одну сторону от плоскости каждого из своих плоских углов.
Теорема.
Сумма плоских углов выпуклого многогранного угла меньше 360 градусов.
Доказательство.
Найдем сумму плоских углов. Каждый плоский угол можно выразить через сумму углов треугольника, который образуется парой ребер и плоскостью, пересекающей все ребра многогранного угла. Далее вынесем из под скобок 180 градусов и перегруппируем в скобках углы так, чтобы в скобках была сумма плоских углов трехгранного угла, образованного тремя соседними лучами.
Сумма плоских углов трехгранного угла больше третьего плоского угла, поэтому каждая сумма углов в скобках не больше, чем соответствующий им третий плоский угол. Поэтому искомая сумма не превышает 360 градусов.
Что и требовалось доказать.
Примеры и разбор решения заданий тренировочного модуля
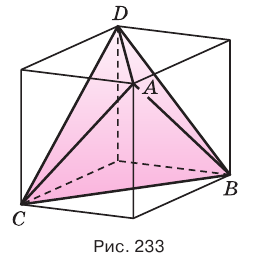
Дан тетраэдр ABCD (рис. 3). В этом тетраэдре углы DAB, DAC и ACB прямые. Ребра AC и CB равны 10 сантиметрам, отрезок DB равен 10
сантиметров. Необходимо найти двугранный угол ABCD.
Решение
По условию прямая DA перпендикулярно прямым AB и AC. Тогда по признаку перпендикулярности прямой и плоскости прямая DA перпендикулярна ABC.
Тогда прямая DA – перпендикуляр к плоскости ABC. Прямая DC – наклонная, а AC – проекция. По условию прямая AC перпендикулярна прямой BC. Тогда по теореме о трех перпендикулярах наклонная DC перпендикулярна прямой BC. Это означает, что угол ACD является линейным углом искомого двугранного угла. Из прямоугольного треугольника DCB найдем DC по теореме Пифагора. 
Из прямоугольного треугольника ACD теперь можно выразить косинус угла ACD. 
= 60°.
В трехгранном угле два плоских угла равны 115.8º и 97º. Если величина третьего плоского угла задается целым числом градусов, то ее наибольшее значение равно?
Обозначим величину третьего плоского угла за X. Воспользуемся теоремой о сумме плоских углов многогранного угла: сумма плоских углов многогранного угла меньше 360º. Следовательно, можно записать неравенство:
Правильные многогранники в геометрии с примерами
Пусть есть плоский многоугольник 
Многогранный угол называется выпуклым, если он расположен по одну сторону от плоскости любой его грани. Многогранный угол на рисунке 228 выпуклый, а на рисунке 229 — невыпуклый. По количеству граней многогранные углы разделяют на трехгранные, четырехгранные и т. д.
Теорема 12.
Сумма плоских углов выпуклого многогранного угла меньше 360°.
Доказательство:
Установим сначала, что каждый плоский угол трехгранного угла меньше суммы двух других его углов.
Пусть есть трехгранный угол 
(рис. 230). Пусть для определенности угол 
— больший из плоских углов трехгранного угла. В плоскости грани 
от луча 
отложим угол 
, равный углу 
, и на лучах 
и 
отложим равные отрезки 
и 
. Через прямую 
проведем такую плоскость, которая пересекает ребра 
и в некоторых точках 
и 
. Треугольники 
и 
равны, так как у них сторона 
общая, и по построению равны углы 
и 
, а также стороны 
и 
. Значит, 
Далее по свойству сторон треугольника получаем 
или 
или 
Теперь, поскольку у треугольников 
и 
сторона 
общая, стороны и равны, но 
, то 
Прибавив к левой и правой частям этого неравенства соответственно углы и , которые равны друг другу, получим, что 
или 
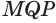
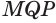
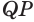
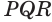
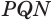
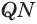
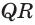
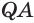
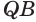
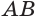
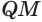
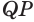
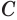
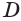
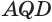
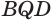
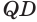
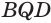
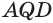
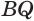
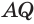
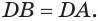
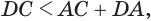
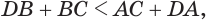
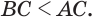
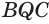
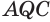
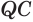
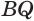
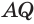
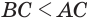
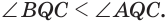
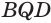
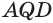
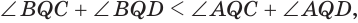
Пусть теперь есть выпуклый многогранный угол с вершиной 
(рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник 
каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем:
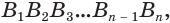
Сложим покомпонентно эти неравенства:
Теперь обратим внимание на то, что сумма в левой части последнего неравенства есть сумма углов многоугольника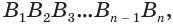 
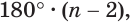
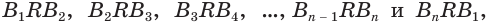
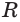
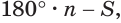
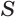
которая равна 
а в правой — сумма углов всех треугольников 
но без их углов при вершине , которая равна 
где 
выражает сумму плоских углов данного многогранного угла. Таким образом,
Многогранник, у которого все грани являются равными правильными многоугольниками и все двугранные углы равны друг другу, называется правильным многогранником.
Из этого определения следует, что у правильного многогранника равны друг другу все его:
Теорема 13.
Количество ребер, сходящихся в каждой вершине правильного многогранника, не больше пяти.
Доказательство:
Допустим, что это не так, т. е. в вершине многогранника сходится шесть или больше ребер. Тогда при этой вершине многогранник имел бы шесть или больше равных плоских углов. Учитывая, что сумма этих углов меньше 360°, получаем, что каждый из них меньше 60°. Но это невозможно, поскольку гранями правильного многогранника являются правильные многоугольники, а у них углы не меньше 60°.
Теорема 14.
Количество сторон правильного многоугольника, являющегося гранью правильного многогранника, не больше пяти.
Доказательство:
В каждой вершине правильного многогранника сходится не менее трех плоских углов, а поэтому каждый из них должен быть меньше 120°. Вместе с этим угол правильного шестиугольника равен 120°, а угол правильного многоугольника с большим количеством сторон больше 120°. Поэтому правильные многоугольники, количество сторон которых больше пяти, не могут быть гранями правильного многоугольника.
Теорема 15.
Есть пять типов правильных многогранников.
Доказательство:
В соответствии с теоремой 14 гранями многогранника могут быть правильные треугольники, четырехугольники или пятиугольники.
Если гранями правильного многогранника служат треугольники, то, с учетом теоремы 13, в вершинах многогранника могут сходиться три, четыре или пять ребер. Если гранями правильного многогранника служат четырехугольники или пятиугольники, то в вершинах многогранника может сходиться только три ребра. Значит, существует не более пяти видов правильных многогранников.
Чтобы убедиться, что такие виды многогранников существуют, достаточно указать способ построения каждого из них.
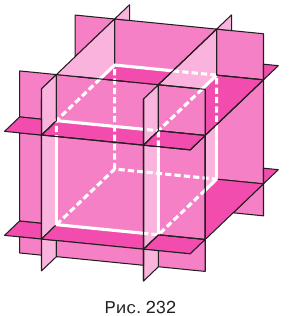
Прежде всего отметим, что правильным многогранником, гранями которого служат правильные четырехугольники, т. е. квадраты, является куб, который еще называют правильным гексаэдром. Куб можно построить так. В произвольно выбранной плоскости построить квадрат, через его стороны провести плоскости, перпендикулярные выбранной плоскости, и провести еще одну плоскость, параллельную выбранной плоскости и отстоящую от нее на сторону квадрата (рис. 232). Мы видим, что гексаэдр имеет 6 граней, 12 ребер и 8 вершин.
Построение многогранника, в каждой вершине которого сходится по три треугольные грани, может быть таким. Построить куб. Выбрать одну из его вершин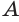 
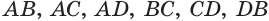
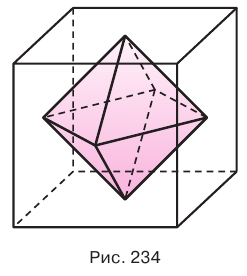
и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине 
. Пусть это вершины 
, 
, 
. Точки , , , 
являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков 
является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде 
все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Построение многогранника, в каждой вершине которого сходится по четыре треугольные грани, может быть таким. Построить куб и найти центры шести его граней (рис. 234). Эти точки являются вершинами многогранника, все грани которого — правильные треугольники. Такой многогранник называется правильным октаэдром. Октаэдр имеет 8 граней, 12 ребер и 6 вершин.
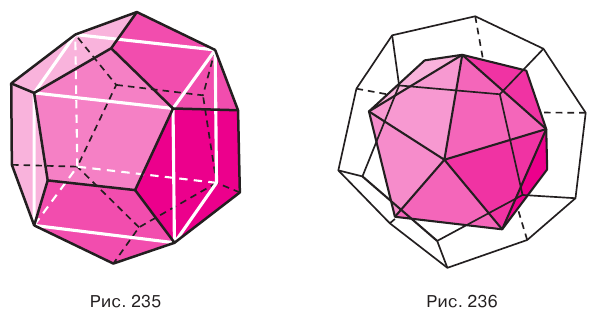
Построение многогранника, в каждой вершине которого сходится по три пятиугольные грани, можно выполнить, снова используя куб. Если через каждое из двенадцати ребер куба провести плоскость, которая не имеет с поверхностью куба других общих точек, кроме точек этого ребра, то полученные 12 плоскостей при пересечении дадут грани некоторого многогранника. Можно так подобрать наклон этих плоскостей к граням куба, что грани этого двенадцатигранника будут правильными пятиугольниками (рис. 235). Такой многогранник называется правильным додекаэдром. Додекаэдр имеет 12 граней, 30 ребер и 20 вершин.
Наконец, многогранник, в каждой вершине которого сходится по пять треугольных граней, можно построить, используя додекаэдр: центры граней додекаэдра являются вершинами искомого правильного многогранника (рис. 236). Такой многогранник называется правильным икосаэдром. Икосаэдр имеет 20 граней, 30 ребер и 12 вершин.
Таким образом, есть пять типов правильных многогранников.
Названия правильных многогранников происходят из греческого языка. Термин тетраэдр, по-гречески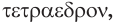 
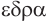
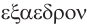
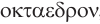
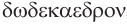
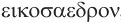
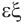
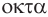
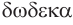
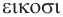
означает четырехгранник: 
— четыре и 
— грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески 
, 
, 
, 
, означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник: 
, — шесть, 
— восемь, 
— двенадцать, 
— двадцать.
Мы знаем, что правильные гексаэдр и тетраэдр имеют описанный и вписанный шары. Также описанный и вписанный шары имеют октаэдр, додекаэдр и икосаэдр. Центры этих шаров совпадают, и эта точка является центром симметрии соответствующего правильного многогранника, кроме тетраэдра, который не имеет центра симметрии.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.