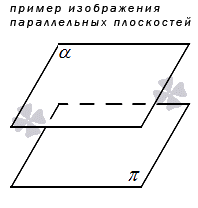
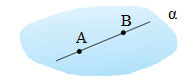
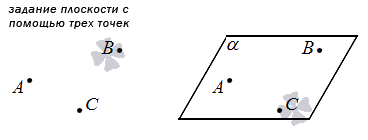Что такое плоскость в геометрии 7 класс определение
Плоскость

Всего получено оценок: 107.
Всего получено оценок: 107.
Плоскость – это основная единица планиметрии. Для правильного восприятия сложных фигур, таких как, пирамида, конус или призма, необходимо понимать и, главное, представлять себе, что такое плоскость.
Определение плоскости
Плоскость представляет поверхность, содержащую прямые, соединяющие две любые ее точки. Это определение звучит достаточно запутанно, поэтому лучше его запомнить. А для понимания стоит запомнить, что плоскость это прямая поверхность. Любая грань пирамиды это плоскость, так же как стена, поверхность стола или лист бумаги.
Стена является частью плоскости, так как любой другой пример плоскости из реальной жизни это ограниченное пространство, а плоскость безгранична, так же как и линия.
Из плоскостей в планиметрии составляются фигуры, как в стереометрии из линий. Яркий пример: четырехугольная пирамида, которая состоит из пяти граней, каждая из которых является частью отдельной плоскости.
Геометрия состоит из двух разделов: планиметрия и стереометрия. Фигуры на плоскости, состоящие из линий и точек это раздел стереометрии. Планиметрия изучает фигуры из плоскостей, прямых и точек. Проще говоря, планиметрия – это геометрия объемных фигур.
Способы задания плоскостей
Плоскость может быть задана тремя точками, нележащими на одной прямой. Из этого утверждения следуют еще два варианта задания плоскостей. При этом специального знака плоскостей не существует.
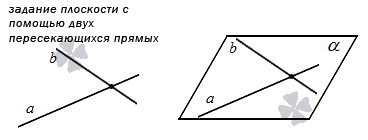
Плоскость можно задать двумя пересекающимися прямыми, тогда одной точкой будет служить точка пересечения прямых, а двумя другими произвольные точки на одной и второй прямой.
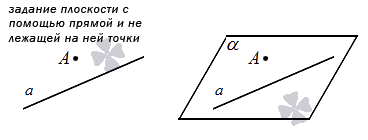
Еще один вид это задание прямой и точкой, нележащей на этой прямой. По аналогии со вторым вариантам: одна точка уже есть и не лежит на прямой, а две других это произвольные точки имеющейся линии.
Взаимное расположение прямой и плоскости
Прямая в пространстве может быть параллельной плоскости, лежать в плоскости и пересекать ее. Рассмотрим каждый вариант более подробно.
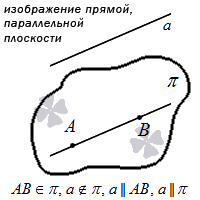
Прямая параллельная плоскости, если она не имеет общих точек с ней. Признак параллельности прямой и плоскости крайне прост: прямая параллельна плоскости, если параллельна любой прямой лежащей в этой плоскости.
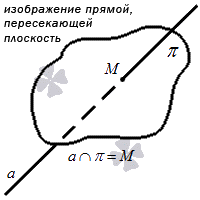
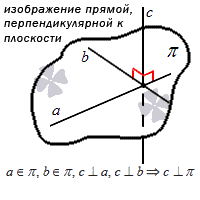
Прямая в пространстве может пересекать плоскость, если имеет с ней одну общую точку. Обратите внимание, что тогда прямая и плоскость образуют угол. Чтобы его увидеть, необходимо провести прямую в плоскости через точку пересечения. Тогда угол между этими прямыми и будет углом между прямой и плоскостью. Кроме того, прямая может быть перпендикулярна плоскости. Признак перпендикулярности прямой и плоскости звучит так: прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых в этой плоскости и пересекает плоскость в месте пересечения этих прямых.
Прямая в пространстве может лежать в плоскости, если две любые точки этой прямой принадлежат этой плоскости.
Взаимное расположение плоскостей
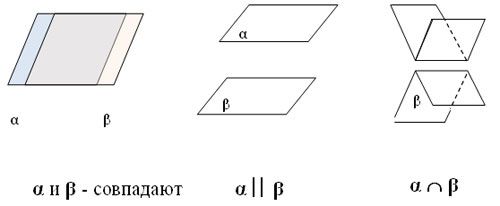
Плоскости в пространстве могут совпадать, пересекаться или быть параллельными.
Плоскости параллельны, если попарно параллельны две пересекающиеся прямые в каждой из плоскостей.
Пересекаться плоскости могут только по прямой. В этом случае плоскости образуют угол. Чтобы найти его численные значения нужно в каждой из плоскостей провести прямую перпендикулярную прямой пересечения плоскостей. Эти две прямые и образуют угол плоскостей. Эти свойства иногда называют правилами плоскостей.
Что мы узнали?
Мы дали определение и привели примеры плоскости. Выделили варианты пересечения прямой и плоскости и пересечения плоскостей. Привели несколько признаков, относящихся с плоскостям и разобрали все случаи существования плоскостей в пространстве.
Плоскость в пространстве – необходимые сведения
Плоскость – это одна из наиболее важных фигур в планиметрии, поэтому нужно хорошо понимать, что она из себя представляет. В рамках этого материала мы сформулируем само понятие плоскости, покажем, как ее обозначают на письме, и введем необходимые обозначения. Затем мы рассмотрим это понятие в сравнении с точкой, прямой или другой плоскостью и разберем варианты их взаимного расположения. Все определения будут проиллюстрированы графически, а нужные аксиомы сформулированы отдельно. В последнем пункте мы укажем, как правильно задать плоскость в пространстве несколькими способами.
Понятие плоскости и ее обозначения
Плоскость представляет собой одну из простейших фигур в геометрии наравне с прямой и точкой. Ранее мы уже объясняли, что точка и прямая размещаются на плоскости. Если эту плоскость разместить в трехмерном пространстве, то мы получим точки и прямые в пространстве.
В жизни представление о том, что такое плоскость, нам могут дать такие объекты, как поверхность пола, стола или стены. Но нужно учитывать, что в жизни их размеры ограничены, а здесь понятие плоскости связано с бесконечностью.
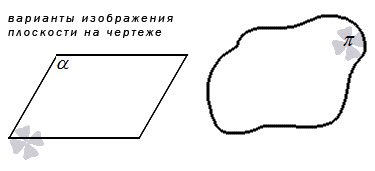
Если нам нужно графическое отображение плоскости, то обычно для этого используется замкнутое пространство произвольной формы или параллелограмм.
Плоскость принято рассматривать вместе с прямыми, точками, другими плоскостями. Задачи с этим понятием обычно содержат некоторые варианты их расположения друг относительно друга. Рассмотрим отдельные случаи.
Как могут располагаться плоскость и точка друг относительно друга
Первый способ взаимного расположения заключается в том, что точка расположена на плоскости, т.е. принадлежит ей. Можно сформулировать аксиому:
В любой плоскости есть точки.
Если некая плоскость задана в пространстве, то число точек, принадлежащих ей, является бесконечным. А какого минимального количества точек будет достаточно для определения плоскости? Ответом на этот вопрос будет следующая аксиома.
Через три точки, которые не расположены на одной прямой, проходит единственная плоскость.
Другой способ взаимного расположения точки и плоскости можно выразить с помощью третьей аксиомы:
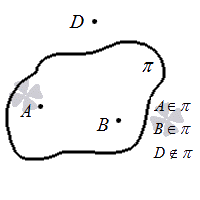
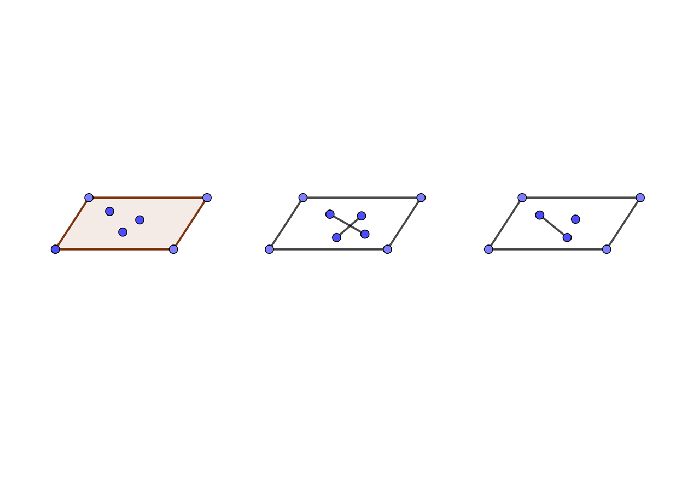
Можно выделить как минимум 4 точки, которые не будут находиться в одной плоскости.
Графически последнюю аксиому можно представить так:
Варианты взаимного расположения прямой и плоскости
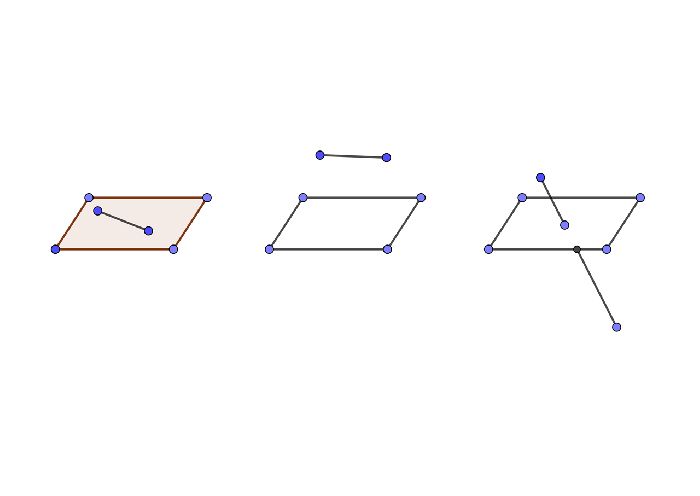
Самый простой вариант – прямая находится в плоскости. Тогда в ней будут расположены как минимум две точки этой прямой. Сформулируем аксиому:
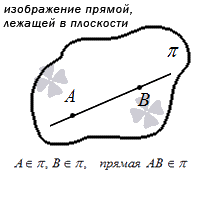
Если хотя бы две точки заданной прямой находятся в некоторой плоскости, это значит, что все точки этой прямой расположены в данной плоскости.
Графически этот вариант расположения выглядит так:
Если мы решаем задачу, в которой есть плоскость, нам необходимо знать, что из себя представляет нормальный вектор плоскости.
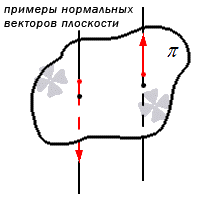
Нормальный вектор плоскости – это такой вектор, который лежит на перпендикулярной прямой по отношению к плоскости и не равен при этом нулю.
Примеры нормальных векторов плоскости показаны на рисунке:
Если прямая расположена внутри плоскости, то она делит ее на две равные или неравные части (полуплоскости). Тогда такая прямая будет называться границей полуплоскостей.
Любые 2 точки, расположенные в одной полуплоскости, лежат по одной сторону от границы, а две точки, принадлежащие разным полуплоскостям, лежат по разную сторону от границы.
Варианты расположения двух плоскостей друг относительно друга
1. Наиболее простой вариант – две плоскости совпадают друг с другом. Тогда они будут иметь минимум три общие точки.
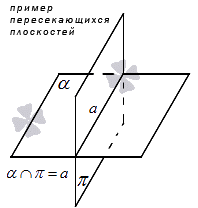
2. Одна плоскость может пересекать другую. При этом образуется прямая. Выведем аксиому:
Если две плоскости пересекаются, то между ними образуется общая прямая, на которой лежат все возможные точки пересечения.
На графике это будет выглядеть так:
В таком случае между плоскостями образуется угол. Если он будет равен 90 градусам, то плоскости будут перпендикулярны друг другу.
3. Две плоскости могут быть параллельными друг другу, то есть не иметь ни одной точки пересечения.
Если у нас есть не две, а три и больше пересекающихся плоскостей, то такую комбинацию принято называть пучком или связкой плоскостей. Подробнее об этом мы напишем в отдельном материале.
Как задать плоскость в пространстве
В этом пункте мы посмотрим, какие существуют способы задания плоскости в пространстве.
1. Первый способ основан на одной из аксиом: единственная плоскость проходит через 3 точки, не лежащие на одной прямой. Следовательно, мы можем задать плоскость, просто указав три таких точки.
Если у нас есть прямоугольная система координат в трехмерном пространстве, в которой задана плоскость с помощью этого способа, то мы можем составить уравнение этой плоскости (подробнее см, соответствующую статью). Изобразим данный способ на рисунке:
2. Второй способ – задание плоскости с помощью прямой и точки, не лежащей на этой прямой. Это следует из аксиомы о плоскости, проходящей через 3 точки. См. рисунок:
3. Третий способ заключается в задании плоскости, которая проходит через две пересекающиеся прямые (как мы помним, в таком случае тоже есть только одна плоскость.) Проиллюстрируем способ так:
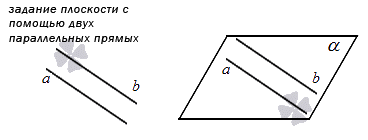
4. Четвертый способ основан на параллельных прямых. Вспомним, какие прямые называются параллельными: они должны лежать в одной плоскости и не иметь ни одной точки пересечения. Получается, что если мы укажем в пространстве две такие прямые, то мы тем самым сможем определить для них ту самую единственную плоскость. Если у нас есть прямоугольная система координат в пространстве, в которой уже задана плоскость этим способом, то мы можем вывести уравнение такой плоскости.
На рисунке этот способ будет выглядеть так:
Если мы вспомним, что такое признак параллельности, то сможем вывести еще один способ задания плоскости:
Если у нас есть две пересекающиеся прямые, которые лежат в некоторой плоскости, которые параллельны двум прямым в другой плоскости, то и сами эти плоскости будут параллельны.
Таким образом, если мы зададим точку, то мы сможем задать плоскость, которая проходит через нее, и ту плоскость, которой она будет параллельна. В таком случае мы тоже можем вывести уравнение плоскости (об этом у нас есть отдельный материал).
Вспомним одну теорему, изученную в рамках курса по геометрии:
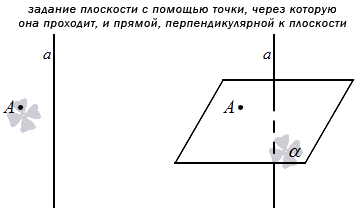
Через определенную точку пространства может проходить только одна плоскость, которая будет параллельна заданной прямой.
Это значит, что можно задать плоскость путем указания конкретной точки, через которую она будет проходить, и прямой, которая будет перпендикулярна по отношению к ней. Если плоскость задана этим способом в прямоугольной системе координат, то мы можем составить уравнение плоскости для нее.
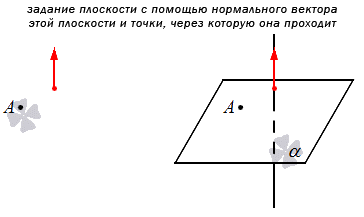
Также мы можем указать не прямую, а нормальный вектор плоскости. Тогда можно будет сформулировать общее уравнение.
Мы рассмотрели основные способы, с помощью которых можно задать плоскость в пространстве.
Плоскость
Понятие плоскости
поверхность школьной доски:
Эти поверхности ограничены, у них есть края. Но представление о плоскости мы имеем с их помощью.
Только плоскость простирается безгранично (в любом направлении, заданном на этой плоскости).
Понятие плоскость принадлежит к числу основных понятий геометрии.
Обозначение плоскости
Конечно, нарисовать плоскость, у которой нет краев, невозможно. Поэтому, при изображении плоскости, рисуют только ее часть:
Обозначается плоскость строчными буквами греческого алфавита – α (альфа), β (бета), γ (гамма) и т.д.:
Буквы пишут либо рядом с плоскостью, либо на плоскости.
Определение плоскости
Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки. ( то есть, любая прямая, соединяющая две ее точки, целиком принадлежит ей).
Поделись с друзьями в социальных сетях:
Термины, определения и формулы по геометрии за 7 класс
Геометрия – наука, занимающаяся изучением геометрических фигур (в переводе с греческого слово «геометрия» означает «землемерие»).
В планиметрии изучаются свойства фигур на плоскости. В стереометрии изучаются свойства фигур в пространстве.
Отрезок — это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка.
Угол — это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.
Лучи называются сторонами угла, а точка — вершиной угла.
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности.
Радиус окружности – отрезок, соединяющий центр окружности с какой-либо её точкой.
Отрезок, соединяющий две точки окружности, называется ее хордой.
Хорда, проходящая через центр окружности, называется диаметром.
Круг — это часть плоскости, ограниченная окружностью.
Угол называется развёрнутым, если обе его стороны лежат на одной прямой. ( Развёрнутый угол равен 180°).
Две геометрические фигуры называются равными, если их можно совместить наложением.
Середина отрезка — это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
Биссектриса угла — это луч, исходящий из вершины угла и делящий его на два равных угла.
Угол называется прямым, если он равен 90°.
Угол называется острым, если он меньше 90° (т.е. меньше прямого угла).
Угол называется тупым, если он больше 90°, но меньше 180°. (т.е. больше прямого, но меньше развёрнутого).
Два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой, называются смежными. Сумма смежных углов равна 180°.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого. Вертикальные углы равны.
Расстоянием от точки до прямой называется длина перпендикуляра, проведённого из этой точки к прямой.
Перпендикулярные прямые — прямые, которые при пересечении образуют прямой угол.
Параллельные прямые — прямые, лежащие в одной плоскости и не имеющие общих точек.
Треугольник — это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой и трех отрезков, соединяющих эти точки. Точки называются вершинами, а отрезки — сторонами треугольника.
Сумма углов треугольника равна 180°.
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Если все три угла треугольника острые, то треугольник называется остроугольным.
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
Если один из углов треугольника прямой, то треугольник называется прямоугольным.
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две стороны, образующие прямой угол — катетами.
(Т. о соотношениях между сторонами и углами треугольника) В треугольнике против большей стороны лежит больший угол, и обратно, против большего угла лежит большая сторона.
В прямоугольном треугольнике гипотенуза больше катета.
(Признак равнобедр. треугольника) Если два угла треугольника равны, то треугольник равнобедренный.
(Т. Неравенство треугольника) Каждая сторона треугольника меньше суммы двух других сторон.
Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.
Теорема – утверждение, справедливость которого устанавливается путём рассуждений. Сами рассуждения называются доказательством теоремы.
Первый признак равенства треугольников
«Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то эти треугольники равны.»
Сокращенно его называют равенство «по двум сторонам и углу между ними».
На рисунке 1 представлен треугольник ABС. Который имеет три вершины (А, В и С). И стороны – АВ, АС и ВС.
Треугольники считаются равными, когда все их стороны и углы соответственно равны друг другу (в случае, когда равны лишь углы, а стороны пропорциональны, треугольники называются подобными). Таким образом очевидно, что равные треугольники можно наложить друг на друга – и они полностью совпадут.
Доказательство первого признака равенства треугольников
Два треугольника: ABC и DEF (рисунок 2).
По условию теоремы две пары отрезков этих треугольников равны между собой (АС = FD и СВ = EF). Углы между отрезками также равны (т.е. ∠АСВ = ∠EFD).
Доказать, что треугольник ABC равен треугольнику DEF.
Поскольку имеется равенство углов (∠АСВ = ∠EFD), треугольники можно наложить друг на друга, так чтобы вершина С совпадала с вершиной F.
При этом отрезки СА и СВ наложатся на отрезки FE и FD.
А поскольку отрезки двух треугольников равны между собой (АС = FD и СВ = EF по условию), то отрезок АВ также совпадёт со стороной ED.
Это в свою очередь даст совмещение вершин А и D, В и Е.
Следовательно, треугольники полностью совместятся, а значит, они равны.
Теорема доказана.
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Как и в доказательстве первого признака, нужно убедиться, достаточно ли этого для равенства треугольников, можно ли их полностью совместить?
1. Так как MN=PR, то эти отрезки совмещаются, если совместить их конечные точки.
2. Так как∡N=∡R и∡M=∡P, то лучи MK и NK наложатся соответственно на лучи PT и RT.
3. Если совпадают лучи, то совпадают точки их пересечения K и T.
4. Совмещены все вершины треугольников, то есть ΔMNK и ΔPRT полностью совместятся, значит они равны.
Третий признак равенства треугольников
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Опять попробуем совместить треугольникиΔMNK и ΔPRT наложением и убедится, что соответственно равные стороны гарантирует и равенство соответственных углов этих треугольников и они полностью совпадут.
Совместим, например, одинаковые отрезки MK иPT. Допустим, что точки N и R при этом не совмещаются.
Пусть O — середина отрезка NR. Соответственно данной информацииMN=PR, KN=TR. Треугольники MNR и KNR равнобедренные с общим основанием NR.
Поэтому их медианы MO и KO являются высотами, значит перпендикулярны NR. Прямые MO и KO не совпадают, так как точки M, K, O не лежат на одной прямой. Но через точку O прямой NR можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.
Доказано, что должны совместиться и вершины N и R.
Третий признак позволяет назвать треугольник очень сильной, устойчивой фигурой, иногда говорят, что треугольник — жёсткая фигура. Если длины сторон не меняются, то углы тоже не меняются. Например, у четырёхугольника такого свойства нет. Поэтому разные поддержки и укрепления делают треугольными.
Перпендикуляр к прямой
Из точки не лежащей на прямой можно провести перпендикуляр к этой прямой и притом только один
Медианы,биссектриссы и высоты треугольника
В любом треугольнике медианы пересекаются в одной точке. Биссектрисы пересекаются в одной точке. Высоты или их продолжения также пересекаются в одной точке
Свойства равнобедренного треугольника
Признаки параллельности двух прямых. Теорема 1
Если при пересечении двух прямых секущей накрест лежащие углы равны то прямые параллельны.
Признаки параллельности прямых.Теорема 2
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Признаки параллельности прямых. Теорема 3.
Если при пересечении двух прямых секущей сумма односторонних углов равна 180⁰ то прямые параллельны.
Теорема об углах образованных двумя параллельными прямыми и секущей.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Аксиома параллельных прямых.
В одной плоскости с заданной прямой через точку, не лежащую на этой прямой, можно провести только одну прямую, параллельную заданной прямой.
Теоремы об углах, образованных двумя параллельными прямыми и секущей
Теорема Сумма углов треугольника равна 180°.
Рассмотрим произвольный треугольник KLM и докажем, что ∡K+∡L+∡M=180°.
Проведём через вершину L прямую a, параллельную стороне KM.
Углы, обозначенные 1, являются накрест лежащими углами при пересечении параллельных прямых a и KMсекущей KL, а углы, обозначенные 2 — накрест лежащими углами при пересечении тех же параллельных прямых секущей ML.
Очевидно, сумма углов 1, 2 и 3 равна развёрнутому углу с вершиной L, т. е.
∡1+∡2+∡3= 180°или ∡K+∡L+∡M=180°.
Следствия из теоремы о сумме углов треугольника
Следствие 1. Сумма острых углов прямоугольного треугольника равна 90°.
Следствие 2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
Следствие 3. В равностороннем треугольнике каждый угол равен 60°.
Следствие 4. В любом треугольнике либо все углы острые, либо два угла острые, а третий — тупой или прямой.
Следствие 5. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Из равенств ∡KML+∡BML= 180° и ∡K+∡L+∡KML=180° получаем, что ∡BML=∡K+∡L.
Четырёхугольники
Многоугольник — фигура, состоящая из нескольких точек плоскости, поочередно соединённых между собой непересекающимися отрезками.
Выпуклый многоугольник — это многоугольник, который весь лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
Теорема:Сумма внутренних углов выпуклого n-угольника равна (n-2)*1800.
Параллелограмм- это четырёхугольник, у которого противоположные стороны попарно параллельны.
Свойство:в параллелограмме противоположные стороны равны и противоположные углы равны.
Свойство:диагонали параллелограмма точкой пересечения делятся пополам.
Теорема(признакпараллелограмма): Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма): Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
Теорема(признак параллелограмма): Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.Параллельные стороны-основания, непараллельные стороны-боковые.
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Прямоугольная трапеция — это трапеция, у которой один из углов прямой.
Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пресекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойство: диагонали прямоугольника равны.
Теорема(признакпрямоугольника): если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Ромб — это параллелограмм, у которого все стороны равны.
Свойство: диагонали ромба взаимно перпендикулярны и делят его углы пополам.
Квадрат — это прямоугольник, у которого все стороны равны.
Площадь
Площадь плоской фигуры-это количество единичных квадратов, вмещающихся в данную фигуру.
Площадь квадрата равна квадрату его стороны.
Площадь прямоугольника равна произведению его смежных сторон.
Площадь параллелограмма равна произведению его основания на высоту.
Площадь треугольника равна половине произведения его основания на высоту.
Площадь прямоугольного треугольника равна произведению его катетов.
Если высоты двух треугольников равны, то их площади относятся как основания.
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Площадь трапеции равна полусумме её оснований на высоту.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Теорема(обр.): если квадрат одной стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Подобные треугольники
Отрезки m и n пропорциональны отрезкам m1и n1,если отношения их длин равны m:m1= n: n1.
Подобные треугольники — это треугольники,у которых соответственные углы равны, а сходственные стороны пропорциональны.
Коэффициент подобия — это число, равное отношению сходственных сторон подобных треугольников.
Теорема: Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Свойство биссектрисы тр-ка: биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Теорема(первый признак подобия треугольников): если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
Теорема(второй признак подобия треугольников): если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.
Теорема(первый признак подобия треугольников): если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
Средняя линия треугольника – это отрезок, соединяющий середины двух его сторон.
Теорема: Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Среднее пропорциональное(среднее геометрическое)двух величин – это квадратный корень из произведения этих величин.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
С. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы,заключённым между катетом и высотой, проведённой из вершины прямого угла.
Синус острого угла прямоугольного треугольника — это отношение противолежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника- это отношение прилежащего катета к гипотенузе.
Окружность
Касательная к окружности – это прямая, имеющая с окружностью только одну общую точку.
Т. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Т.(обр.) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной.
Центральный угол – это угол с вершиной в центре окружности.
Дуга окружности измеряется центральным углом, который на неё опирается.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Т.Вписанный угол равен половине дуги, на которую он опирается.
С. Вписанные углы, опирающиеся на одну и ту же дугу, равны.
С. Вписанный угол, опирающийся на полуокружность, — прямой.
Т. Если две хорды окружности пересекаются, произведение отрезков одной хорды равно произведению отрезков другой хорды.