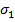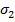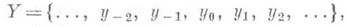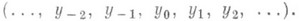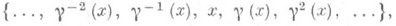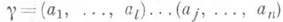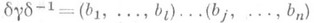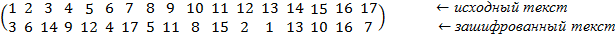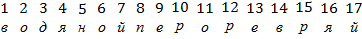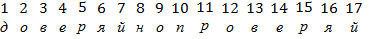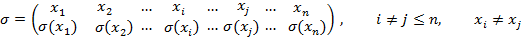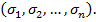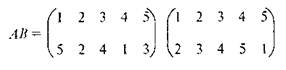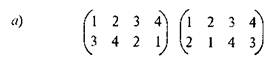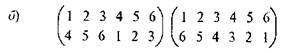Что такое подстановка в алгебре

ПОДСТАНОВКА

(*)

что для любого целого i s(y i )=y i+1 Обозначение бесконечного цикла таково:

Цикл длины 2 есть транспозиция. Группа S n содержит ( п-1)! циклов длины п. Для любой подстановки g из S(X).существует такое разбиение множества X на непересекающиеся подмножества, что на каждом из них g действует как цикл. Конечные подмножества этого разбиения имеют вид

где при . Циклы, индуцируемые подстановкой Y на подмножествах разбиения, наз. независимыми циклами подстановки g. Например, (1, 3, 4) и (2, 5)- независимые циклы П.

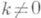
g записывается в виде

Из независимых циклов данной П. можно получить независимые циклы П., сопряженной с ней. Напр., если

П. возникли впервые в комбинаторике 18 в. В кон. 18 в. Ж. Лагранж (J. Lagrange) применил их при исследовании разрешимости алгебраич. уравнении в радикалах. О. Коши (A. Cauchy) посвятил многочисленные исследования этому понятию. Ему, в частности, принадлежит идея разложения П. в произведение циклов. Исследования групповых свойств П. восходит к Н. Абелю (N. Abel) и особенно к Э. Галуа (Е. Galois). См. Галуа теория, Подстановок группа.

Лит.:[1] Jordan С., Traite des substitutions et des equations altfebriques, P., 1057; [2] Кострикин А. И., Введение в алгебру, М., 1977; [3] Курош А. Г., Курс высшей алгебры, 11 изд., М., 1975; [4] Холл М., Теория групп, пер. с англ., М., 1962. Д. А. Супруненко.

Полезное

Смотреть что такое «ПОДСТАНОВКА» в других словарях:

подстановка — замена, замещение; подмена, субституция, смена, подстановление, перемена Словарь русских синонимов. подстановка см. замена Словарь синонимов русского языка. Практический справочник. М.: Русский язык. З. Е. Александрова … Словарь синонимов

ПОДСТАНОВКА — ПОДСТАНОВКА, подстановки, жен. (книжн.). Действие по гл. подставить в 4 знач. подставлять; замена одного другим. Решить задачу без подстановки буквенных показателей. Подстановка целого числа. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

ПОДСТАНОВКА — см. подставить. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

подстановка — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN substitution … Справочник технического переводчика

Подстановка — Это статья о подстановке как о синтаксической операции над термами. Возможно, вас интересует перестановка. В математике и компьютерных науках подстановка это операция синтаксической замены подтермов данного терма другими термами, согласно… … Википедия

Подстановка — элементов данного множества (математическая), замена каждого из его элементов а каким либо другим элементом φ(а) из того же множества; при этом должны получаться все элементы исходного множества и каждый только один раз. Таким образом,… … Большая советская энциклопедия

ПОДСТАНОВКА — Лавочная подстановка. Пск. Шутл. О женщине маленького роста. СПП 2001, 61 … Большой словарь русских поговорок

Подстановка — ж. действие по гл. подстановить Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой

Источник

Понятие о подстановке и перестановке. Алгебра

Понятие о подстановке и перестановке. Алгебра

ТЕОРЕМА 1. Существует n! различных перестановок n-ой степени из n чисел.

Доказательство:

Пример: Рассмотрим перестановку шестого порядка: 2, 5, 1, 4, 6, 3

1 – две инверсии, затем единицу вычеркнем из перестановки; теперь возьмём двойку и подсчитаем, сколько чисел стоит левее двойки; 2 – ноль инверсий; вычёркиваем двойку и принимаемся за тройку; левее тройки стоит три числа, то есть тройка даёт нам три инверсии; вычёркиваем тройку и считаем, сколько чисел будет левее четвёрки; четвёрка даёт одну инверсию, вычёркиваем четвёрку и считаем количество чисел левее пятёрки; пятёрка даёт 0 инверсий, вычёркиваем пятёрку и считаем количество инверсий, которые даёт шестёрка; шестёрка даёт 0 инверсий.

1 – две инверсии; 2 – ноль инверсий; 3 – три инверсии; 4 – одна инверсия; 5 – ноль инверсий; 6 – ноль инверсий.

Определение 4. Транспозицией называется такое преобразование перестановки, при котором какие – либо два её элемента меняются местами, а все остальные элементы остаются на своих местах.

Теорема 2 . Все n! перестановок можно записать в таком порядке, что каждая следующая будет получаться из предыдущей с помощью одной транспозиции ( такой порядок называется идеальным), при этом ни одна перестановка не встретится дважды, а начинать можно с любой перестановки. Доказательство опустим.

Следствие из теоремы 2 : из какой–либо перестановки n-ой степени можно получить любую другую перестановку n-ой степени с помощью нескольких транспозиций.

Определение 5 . Подстановкой n-ой степени называется любое отображение множества натуральных чисел от 1 до n самого на себя.

Каждую подстановку будем записывать в две строки, предполагая, что под каждым числом записано именно то число, которое ему соответствует. Заметим, что порядок чисел в верхней строчке является несущественным, например, рассмотрим подстановку пятой степени:

Здесь и в той и в другой подстановке 1 переходит в 5; 2 переходит в 4; 3 переходит в 2; 4 переходит в 3 и 5 переходит в 1. Поэтому эти подстановки тождественные. Каждую подстановку можно записывать так, чтобы все числа в первой строке располагались в порядке возрастания. При такой записи подстановок любые две подстановки одной степени будут отличаться только перестановками во второй строке. Отсюда следует довольно простой и важный вывод : существует n! различных подстановок n – ой степени.

Определение 6 . Будем называть подстановку чётной, если общее количество инверсий, содержащихся и впервой и во второй строчках чётное число и нечётной, если общее число инверсий в двух строчках – число нечётное.

Источник

05. Перестановки и подстановки

Мы получили два эквивалентных определения определителя третьего порядка (формулы (4) и (5)). С помощью (4) определитель 3-го порядка вводится с помощью определителей второго порядка (разложение по столбцу). При этом легко проверяется, что все столбцы равноправны. Аналогично рекуррентным образом можно определить определитель n-го порядка (определитель квадратной матрицы n-го порядка), т. е.

=

= (7)

Но в этом случае уже не так просто, как для определителя третьего порядка, проверить, что разложения по остальным столбцам или строкам дают тот же самый результат. Поэтому чаще всего используют в качестве исходного другой подход к определению определителя n-го порядка. Но при этом используются в качестве вспомогательного материала перестановки и подстановки.

Определение 5. Перестановкой Из N Чисел (или N символов) называется расположение этих чисел (или символов) в любом определённом порядке (без повторений).

Теорема 1. Число перестановок из N Символов равно n!

Доказательство. Составляя перестановку, в качестве первого её элемента можно выбрать точно n символов. Если первый элемент выбран, то в качестве второго элемента можно выбрать любой из оставшихся (n – 1) символов. Следовательно, первые два места можно заполнить n×(n – 1 ) способами. Если два места в перестановке уже заполнены, то на третье место можно поставить любой из оставшихся (n – 2) символов. Следовательно, первые три места можно заполнить n×(n – 1)×(n – 2 ) способами. Продолжая этот процесс, получим, что все n мест в перестановке можно заполнить n×(n – 1)×(n – 2)×…×3×2×1 = n! способами.

Говорят, что числа К и Р образуют в перестановке (…К…р…) Инверсию, если К > Р, Но в перестановке К стоит раньше Р. Перестановка называется Чётной, если она содержит чётное число инверсий. Перестановка называется Нечётной, если она содержит нечётное число инверсий.

Пример. 1) Перестановка (9, 7, 1, 3, 4, 8, 5, 2, 6) чётная. В ней число 9 образует инверсии со всеми стоящими за ней числами, их 8. Число 7 образует новые инверсии со всеми стоящими за ней числами, кроме числа 8, их 6. Число 1 не образует ни одной новой инверсии. Числа 3 и 4 образуют по одной новой инверсии с числом 2. Число 8 образует ещё инверсии с 5, 2 и 6, их 3. Число 5 образует инверсию с числом 2. Итак, получается 8 + 6 + 1 + 1 + 3 + 1 = 20 инверсий.

2) Перестановка ( 2, 1, 3, 5, 4, 6, 9, 8, 7) нечётная. В ней инверсии образуют пары чисел 2 и 1, 5 и 4, 9 и 8, 9 и 7, 8 и 7. Получилось 5 инверсий.

Если в перестановке два символа поменять местами, а все остальные символы оставить на старых местах, то получим новую перестановку. Это преобразование перестановки называется Транспозицией.

Теорема 2. Всякая транспозиция меняет чётность перестановки.

Доказательство. Пусть в перестановке символы К и Р меняются местами. При этом возможны два случая.

1) Символы К и Р В данной перестановке стоят рядом, т. е. (…К, Р …). После транспозиции получится перестановка (….Р, к …). Если К и Р Составляли инверсию в данной перестановке, то после инверсии они уже не будут составлять инверсию и наоборот. Число инверсий, которые К и Р Составляли в данной перестановке с остальными символами, не изменится. Следовательно, число инверсий изменится на 1, т. е. чётность перестановки изменится.

2) Символы К и Р В данной перестановке стоят не рядом, т. е. (….К,…,р…). После транспозиции получится перестановка (…Р,…,к…). Число инверсий, которые К и Р Составляли в данной перестановке с символами, стоящими перед К И после Р, не изменится. Если между К и Р Стоят M символов, то переставить К и Р можно следующим образом: переставить К последовательно с каждым из этих M Символов, затем переставить К и Р, затем в обратном порядке переставить Р с каждым из этих M символов. Получим 2m + 1 транспозиций соседних символов. По доказанному каждая из них меняет чётность перестановки. Итак, чётность перестановки изменилась.

Следствие. При n > 1 число чётных перестановок равно числе нечётных перестановок и равно 0,5×n!.

Определение 6. Подстановкой из N символов ( или Подстановкой N-ой степени) называется любое взаимнооднозначное отображение множества этих символов на себя.

Элементы данного множества будем обозначать 1, 2, …, n. Подстановка А может быть записана так: если число К переходит в число aК, то А = . Если в записи подстановки А Некоторые столбцы поменять местами, то получится то же самое отображение данного множества, т. е. та же подстановка. Например,

А = = .

Запись подстановки А = будем называть стандартной. Всякую подстановку можно записать в стандартном виде. Верхнюю и нижнюю строки подстановки можно рассматривать как перестановки. Подстановка А называется чётной, если её верхняя и нижняя строки есть перестановки одинаковой чётности, т. е. общее число инверсий в них – чётное. В противном случае А Называется Нечётной. Так как перестановка столбцов равносильна транспозиции как в верхней так и в нижней строке, то при перестановке столбцов чётность подстановки не изменится, поэтому чётность подстановки можно вычислять по её стандартному виду и в этом случае она совпадает с чётностью нижней строки.

Подстановка Е = называется Тождественной Или Единичной.

Произведением двух подстановок одного и того же порядка называется результат последовательного выполнения тех отображений, которые задают эти подстановки. Например, если А = , В = , то

А×В = . Действительно, первая подстановка переводит 1 в 5, вторая переводит 5 в 4, следовательно, окончательно 1 перейдёт в 4. Аналогично, , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, ; , , следовательно, .

Аналогично получаем, что В×А = . Отсюда следует, что умножение подстановок не подчиняется коммутативному закону. Но можно проверить, что (А×В)×С = А×(В×С) для любых подстановок А, В, С Одного и того же порядка. Очевидно, А×Е = Е×А для любой подстановки А, Если А и Е Одного порядка. Для подстановок А = и В = очевидно А×В = В×А = Е. Следовательно, А-1 = В, т. е. каждая подстановка имеет обратную.

Источник

Лекция № 8 Понятие подстановки. Элементы алгебры подстановок. Использование подстановок в тайнописи

Цель:рассмотреть понятие подстановки, тождественной подстановки,

объяснить, как выполняются действия умножения подстановок, нахождения обратной подстановки,

перечислить свойства произведения подстановок,

рассмотреть понятия инверсии, четности-нечетности подстановок

показать, как подстановки применяются в тайнописи

Получил как-то Фома от одного из своих друзей телеграмму. Эта телеграмма была какой-то странной. Вот что в ней было написано: «йажзеирпончорс медж».

Сможете ли вы «прочитать» этот текст? Фома же, немного подумав, понял секрет этой телеграммы. Его приглашали в гости. Он решил ответить в том же духе. Сочинил ответную телеграмму и зашифровал ее таким же способом. Получилась запись из двух строк:

«приеду в субботу встречайте»,

После окончания шифровки Фома захотел всю свою переписку с другом вести только зашифрованными текстами, меняя время от времени способ шифровки. Поэтому он рьяно взялся за разработку метода шифрования.

Буквы исходного текста он решил заменять номерами позиций, которые занимают эти буквы. Вот какой список номеров получил Фома для телеграммы друга:

Затем он заметил, что зашифрованный текст отличается от исходного только измененным порядком буки. Как изменяется порядок букв, легко увидеть с помощью тех же номеров позиций. Например, зашифрованный текст телеграммы друга Фома теперь смог представлять и виде списка:

Сопоставление этих двух списков дает ключ к шиф­ровке текста:

.

Направление стрелок определяет порядок шифровки текста. Например, буква, стоящая в шифруемом тексте в первой позиции, должна занять в зашифрованном тексте 18-ю позицию.

Если направление стрелок сменить на противоположное, то та же двухстрочная таблица будет определять порядок расшифровки текста. Например, буква, стоящая в зашифрованном тексте в 18-й позиции, должна занять в расшифрованном тексте первую позицию.

Наконец, если первая строка будет всегда связана с исходным текстом, то отпадет необходимость в использовании стрелок. (При шифровке исходным текстом является шифруемый текст, а при расшифровке – зашифрованный).

Поняв все это, Фома быстро записал ключ ко 2-ой шифровке своей телеграммы:

Осталось только сообщить каким-либо образом этот ключ своему другу, и тайна переписки гарантирована!

Если идеи Фомы вы поняли, то вот вам зашифрованное любимое его изречение:

Оно зашифровано ключом:

Попробуйте-ка прочитать это изречение!

«Доверяй, но проверяй!»

Вы, вероятно, уже догадываетесь, что шифровальных ключей подобного вида можно придумать очень много. Каждый из них можно представить в виде двухстрочной таблицы:

.

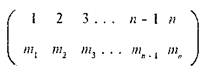
Здесь в верхней строке стоят все натуральные числа от 1 до п в возрастающем порядке. Нижняя строка получается некоторой перестановкой чисел из верхней строки. Вся таблица в целом называется подстановкой порядка п.

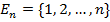
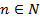
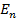
Рассмотрим множество , где , каждый элемент в которой представлен только один раз. Тогда взаимно-однозначное отображение множества на себя называется подстановкой степени п.

Множество подстановок п-й степени обозначается .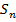

Отношение 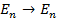бинарное, поэтому подстановки принято записывать в виде двухрядной матрицы, в первой строке которой записаны прообразы, а во второй – их образы:

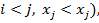
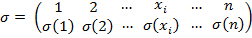
Если прообразы (аргументы) расположены в порядке возрастания (при то запись подстановки такого вида называют канонической. Если аргументы не записаны в порядке возрастания, то, переставляя столбцы (при этом сама подстановка не меняется, а изменяется лишь порядок произношения соответствий), можно верхнюю строку привести к упорядоченному виду:

или

По возможности будем пользоваться именно канонической записью. Такая запись встречалась, когда мы записывали перестановку из п элементов. Отметим, что прообразом перестановки служит произвольное конечное множество, а прообразом подстановки – обязательно .

Найдем число возможных различных подстановок степени п. Поскольку каждой канонической записи подстановки эквивалентна соответствующая перестановка, то число подстановок п-й степени равна числу перестановок из п элементов, т. е. множество состоит из элементов.

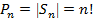
Вернемся к Фоме. С помощью подстановки-ключа

он зашифровал сообщение, состоящее из одного слова, и отправил его другу. Нерасшифрованное сообщение тот зашифровал еще раз, но уже с помощью другого ключа

Получившееся дважды шифрованное сообщение он адресовал вам: «сноас».

Расшифруйте это сообщение. , «сосна»

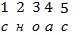
Процесс расшифровки вы можете провести значительно быстрее, если будете знать, как над подстановками выполняется одна алгебраическая операция. Эта операция называется умножением подстановок. (При желании вы можете назвать ее по-другому, ибо она никак не связана с обычным умножением чисел).

Рассмотрим на примере, как она выполняется. Умножим подстановки, с помощью которых шифровалось сообщение Фоме:

Процедура умножения сводится к последовательному проведению подстановок.

В первой подстановке (А): 1 → 5;

во второй подстановке (В): 5 → 1;

В итоге получаем: 1 → 1.

Аналогично, из «2 → 2» и «2 → 3» следует: «2 → 3». Проведя еще три рассуждения такого типа, получим подстановку-произведение

Используя подстановку АВ как шифратор, вы можете теперь в один прием расшифровать сообщение Фомы «сноас». Заодно проконтролируете себя.(ВА= «насос»)

Если вам будет интересно, то можете придумать свои подстановки-шифраторы сообщений и вести тайную переписку с друзьями.

Занимаясь расшифровкой сообщений, вы познакомились с алгебраической операцией над новыми объектами подстановками. Если кого-то из вас заинтересовали не только шифровки, но и сами по себе подстановки, то вы можете лучше познакомиться с ними, выполнив следующие задания.

ЗАДАНИЕ 1. Найдите произведения подстановок:

ЗАДАНИЕ 2.Найдите произведение ВА подстановок А иВ, рассмотренных выше. Используя подстановку ВА как шифратор, расшифруйте еще раз сообщение «сноас». Сравните результат с результатом предыдущей расшифровки. После этого вы сможете сказать, обладает ли умножение подстановок свойством коммутативности.

Пусть заданы две подстановки и , причем

Источник