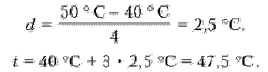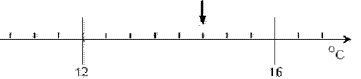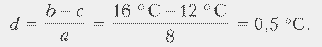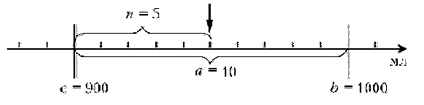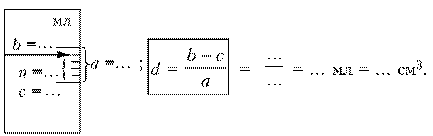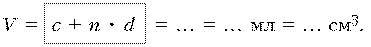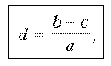Формирование умения снимать показания измерительных приборов

7-й класс. Базовый курс

В 7-м классе, после знакомства с измерительными приборами, я выделяю дополнительно один-два урока (в зависимости от уровня математической подготовки класса) для формирования умения снимать показания измерительных приборов, имеющих шкалу. Можно использовать демонстрационное и лабораторное оборудование (измерительные цилиндры с различной ценой деления, термометры, амперметры, вольтметры и т.д.), а также рисунки шкал приборов в учебниках, задачниках, дидактических карточках.

В процессе эвристической беседы ученики, рассматривая различные измерительные приборы, выделяют их общие признаки и делают записи в тетрадях:

«Шкальный измерительный прибор имеет:

1) шкалу;
2) указатель, перемещающийся по шкале;
3) обозначение единиц измерения физической величины, которую измеряет данный прибор».

Затем они приходят к выводу (и записывают порядок действий в тетрадь), что для снятия показаний приборов необходимо выполнить следующие действия:

1) определить, какая физическая величина измеряется данным прибором;
2) определить цену деления прибора;
3) определить показания прибора.

Далее следует мотивационный этап – я вызываю у учеников затруднение: на доске или на экране (с помощью кодоскопа) демонстрирую шкалу и прошу определить показание.

К сожалению, обычно немногие могут быстро и правильно выполнить это простое задание (хотя определять цену деления семиклассники уже должны уметь из курса математики). Ученик, давший правильный ответ, подробно объясняет, как он рассуждал. Затем семиклассники оформляют рисунок в тетрадях и делают вычисления (один из учеников комментирует). Я показываю записи на экране – для проверки:

Далее я сообщаю: «Сегодня мы будем учиться снимать показания с любой (!) самой сложной шкалы любого (даже незнакомого!) прибора», – и показываю на экране (или на доске) новую шкалу:

Ученики аккуратно делают рисунок в тетрадях и получают учебные инструкционные карты с очень подробным алгоритмом снятия показаний прибора. В инструкционной карте I – два задания. Для выполнения задания 1 необходима таблица (она висит на стене), задание 2 можно пока пропустить или выполнить устно.

Один из учеников читает вслух задания и способы их выполнения. Класс делает записи в тетрадях, я пишу на доске (или использую кодоскоп):

1) °С, температура.
2) Цена деления:

3) Показания прибора: c + n • d.

t = 12 °С + 5 • 0,5 °С = 14,5 °С.

Далее можно начать оформлять задачу № 31 (рис. 9) из задачника В.И.Лукашика (для 7–8-го классов).

Поясняю, что достаточно изобразить участок шкалы, на котором снимают показания (рисовать полностью измерительные цилиндры слишком долго). Затем ученики продолжают работать самостоятельно, по необходимости пользуясь инструкционными картами или с помощью учителя.

На дом дается аналогичное задание: снять показания изображенных на рисунках приборов.

Обычно на отработку и закрепление умения требуется еще один урок (я использую часы из резерва). За это время каждый ученик выполняет разное количество заданий (они могут быть различными и по уровню сложности), что позволяет осуществлять дифференцированный подход. Учитель и сильные ученики оказывают помощь тем, у кого возникают затруднения. Оценивать классные и домашние работы можно выборочно.

На следующем уроке проводится лабораторная работа № 1. Теперь ученики используют полученные знания и умения на практике, работая с реальными физическими измерительными приборами. А учитель, проверяя работу, сможет судить о сформированности навыка снятия показаний.

Лабораторная работа № 1

Цель работы: определить цену деления измерительного цилиндра и научиться определять с его помощью объем жидкости.

Оборудование: измерительный цилиндр с водой.

Задание 1. Определить цену деления измерительного цилиндра.

Задание 2. Определить объем жидкости в измерительном цилиндре.

Перевод единиц из см 3 в м 3 обычно вызывает затруднения. Необходимо обсудить с семиклассниками, как это делается. Сильные ученики быстро выполняют работу и берут измерительные цилиндры с другой ценой деления (или другие приборы). Таким образом, за 2–3 урока удается сформировать обобщенное умение снимать показания со шкальных измерительных приборов и повысить интерес к предмету. Больше к этому вопросу в старших классах мы не возвращаемся.

Снятие показаний приборов

Учебная инструкционная карта I

Задание 1: определить, какая физическая величина измеряется данным прибором.

1) найдите на шкале обозначение единицы физической величины;
2) установите по таблице наименование единицы физической величины, измеряемой данным прибором;
3) установите по таблице, какую физическую величину измеряет данный прибор;
4) прочитайте значения физических величин, указанные на шкале прибора.

Задание 2: определить пределы измерения прибора.

1) определите наименьшее значение физической величины, указанное на шкале прибора. Запишите: «Нижняя граница измерения прибора равна. »;
2) определите наибольшее значение физической величины, указанное на шкале. Запишите: «Верхняя граница измерения прибора равна. »

Учебная инструкционная карта II

Задание: определить цену деления шкалы прибора.

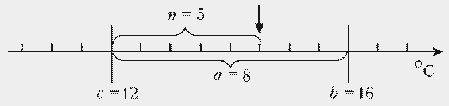
Ценой деления прибора называют значение физической величины, приходящееся на наименьшее деление данного участка шкалы прибора:

b – верхняя граница участка шкалы;
c – нижняя граница участка шкалы;
a – число делений, т.е. число промежутков между черточками от c до b.

Учебная инструкционная карта III

Задание: определить показания прибора.

Полученный результат соответствует значению измеряемой физической величины.

Внимание! Не забывайте при вычислениях указывать единицы физических величин!

Источник

Физические величины и параметры, единицы измерения

Под величинами подразумевают те характеристики явлений, которые определяют явления и процессы и могут существовать независимо от состояния среды и условий. К таким, например, относятся электрический заряд, напряженность поля, индукция, электрический ток и т. д. Среда и условия, в которых протекают явления, определяемые данными величинами, могут изменить эти величины в основном только количественно.

Под параметрами подразумевают такие характеристики явлений, которые определяют свойства сред и веществ и влияют на соотношение между собственно величинами. Они не могут существовать самостоятельно и проявляются лишь в их действии на собственно величины.

К параметрам относятся, например, электрическая и магнитная постоянные, удельное электрическое сопротивление, коэрцитивная сила, остаточная индукция, параметры электрических цепей (сопротивление, проводимость, емкость, индуктивность на единицу длины или объема в данном устройстве) и др.

Значения физических параметров

Значения параметров обычно зависят от условий, в которых протекает данное явление (от температуры, давления, влажности и т. п.), но при постоянстве этих условий параметры сохраняют свои значения неизменными и поэтому называются также постоянными.

Изучение любого явления в физике не ограничивается только установлением качественных зависимостей между величинами, эти зависимости должны быть оценены количественно. Без знания количественных зависимостей нет действительного представления о данном явлении.

Количественно же величина может быть оценена только путем измерения ее, т. е. путем экспериментального сравнения заданной физической величины с одинаковой по физической природе величиной, принятой за единицу измерения.

Измерение может быть прямым или косвенным. При прямом измерении величину, значение которой необходимо определить, непосредственно сравнивают с единицей измерения. При косвенном измерении значения искомой величины находят вычислением по результатам прямых измерений других величин, связанных с данной определенным соотношением..

Установление единиц измерения крайне важно как для развития науки при исследованиях и установления физических законов, так и в практике для ведения технологических процессов, а также для контроля и учета.

Единицы измерения разных величин могут устанавливаться произвольно, без учета связи их с другими величинами, или с учетом таких связей. В первом случае при подстановке числовых значений в уравнение связи необходимо еще дополнительно учитывать эти связи. Во втором случае необходимость в последнем отпадает.

В каждой системе единиц различают основные и производные единицы. Основные единицы устанавливают произвольно, при этом обычно исходят из какого-либо характерного физического явления или свойства вещества или тела. Основные единицы должны быть независимы друг для друга и число их должно определяться необходимостью и достаточностью для образования всех производных единиц.

Так, например, число основных единиц, необходимых для описания электрических и магнитных явлений, равно четырем. В качестве основных единиц не обязательно принимать единицы измерения основных величин.

Важно лишь, чтобы число основных единиц измерения было равно числу основных величии, а также чтобы их можно было воспроизвести (в виде эталонов) с максимальной точностью.

Производными единицами называются единицы, установленные на основании закономерностей, связывающих величину, для которой устанавливается единица, с величинами, единицы которых установлены независимо.

Для получения производной единицы какой-либо величины записывают уравнение, выражающее связь этой величины с величинами, определяемыми основными единицами, и затем, приравняв коэффициент пропорциональности (если он в уравнении имеется) единице, заменяют величины единицами измерения и выражают их через основные единицы. Следовательно, размерность единиц совпадает с размерностью соответствующих величин.

Основные системы единиц в электротехнике

Единицы систем СГС оказались в большинстве случаев неудобными для практики (слишком большими или слишком малыми), что привело к созданию системы практических единиц, кратных единицам системы СГС (ампер, вольт, ом, фарада, кулон и т. д.). Они и были положены в основу получившей в свое время широкое распространение системы МКСА, исходными единицами которой являются метр, килограмм (масса), секунда и ампер.

Удобство этой системы единиц (получившей название абсолютной практической системы) заключается в том, что все ее единицы совпадают с практическими, благодаря чему в формулах связи между величинами, выраженными в этой системе единиц, исчезла необходимость во введении добавочных коэффициентов.

В системе СИ семь исходных единиц: килограмм, метр, секунда, ампер, кельвин, моль, кандела.

Для оценки величин, значительно превышающих по размерам данную единицу измерения, либо значительно меньше ее, применяются кратные и дольные значения единиц. Эти единицы получаются путем присоединения к наименованию основной единицы соответствующей приставки.

Источник

показание

Ценные, полезные показания. | Расхождение в показаниях литературных источников. | По официальным показаниям, нормы завышены.

Свидетельские показания по делу. | Предъявить кому-либо показания. | Давать официальные показания на кого-либо.

Подписать свои показания. | Я просила суд огласить показания свидетеля.

Снять, записать показания. | Показания дозиметра, термометра, барометра.

Показания к операции. | Показания к стационарному лечению.

Антигриппин. Показания: для профилактики и лечения гриппа и ОРВИ.

Полезное

Смотреть что такое «показание» в других словарях:

показание — См. известие, объявление, свидетельство давать показания. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. показание свидетельство, подтверждение, доказательство, указание, симптом;… … Словарь синонимов

ПОКАЗАНИЕ — ПОКАЗАНИЕ, показания, ср. (книжн.). 1. Свидетельство, знак (слово, запись и т.п.), по которому можно судить о чем нибудь. Показания источников о времени этого события расходятся. Собрать показания древних авторов о чем нибудь. 2. Устное или… … Толковый словарь Ушакова

ПОКАЗАНИЕ — в доказательственном праве один из видов доказательств, используемых для установления обстоятельств, которые имеют значение для правильного разрешения гражданских и уголовных дел. Словарь финансовых терминов … Финансовый словарь

показание — ПОКАЗАНИЕ, свидетельство … Словарь-тезаурус синонимов русской речи

ПОКАЗАНИЕ — ПОКАЗАНИЕ, я, ср., обычно мн. 1. Свидетельство, рассказ. Показания очевидцев. 2. Ответ на допросе. П. подсудимого. 3. Величина чего н., показываемая измерительным прибором. П. счётчика. 4. к чему. Данные, указывающие на необходимость или… … Толковый словарь Ожегова

показание — 4.22 показание (indication): Свидетельство, полученное при неразрушающем контроле. Источник: ГОСТ Р ИСО 3183 2009: Трубы стальные для трубопроводов нефтяной и газовой промышленности. Общие технические условия … Словарь-справочник терминов нормативно-технической документации

Показание СИ (X) — 2. Показание СИ (X) значение измеряемой величины, получаемое как непосредственный отсчет СИ (в том числе, после автоматизированной обработки с помощью сопряженного процессора) или после введения обязательных (регламентированных) поправок.… … Словарь-справочник терминов нормативно-технической документации

показание — rodmuo statusas T sritis automatika atitikmenys: angl. indication; reading vok. Ablesung, f; Anzeige, f rus. показание, n pranc. affichage, m; indication, f; lecture, f; relève, m … Automatikos terminų žodynas

показание — rodmuo statusas T sritis Standartizacija ir metrologija apibrėžtis Tai, ką rodo matuoklis. atitikmenys: angl. indication; reading vok. Anzeige, f; Sichtanzeige, f rus. отсчет, m; показание, n pranc. indication, f ryšiai: susijęs terminas –… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

показание — rodomoji vertė statusas T sritis Standartizacija ir metrologija apibrėžtis Matuoklio rodoma vertė, pagrįsta jo gradavimo kreive. atitikmenys: angl. indicated value vok. indizierter Wert, m rus. показание, n pranc. valeur indiquée, f ryšiai:… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

показание — rodmuo statusas T sritis chemija apibrėžtis Matuojamo dydžio vertę atitinkantis įtaiso parodymas. atitikmenys: angl. indication rus. показание … Chemijos terminų aiškinamasis žodynas

Источник

Мощность

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение мощности

Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.

Мощность в физике — это количество работы, которая совершается за единицу времени.

Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.

В электромеханике данная величина тоже связана со скоростью, а конкретно — с тем, как быстро передается ток по участку цепи. Исходя из этого, мы можем рассмотреть еще одно определение.

Мощность — это скалярная физическая величина, которая характеризует скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии.

Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).

Мощность человека в зависимости от деятельности

Вид деятельности

Мощность, Вт

Бег со скоростью 9 км/ч

Плавание со скоростью 50 м/мин

Как обозначается мощность: единицы измерения

В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.

Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.

В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.

Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.

В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.

Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.

Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр. 🐴

Источник

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):

(5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

На точность измерения влияет много факторов, в частности:

Все это необходимо учитывать при проведении измерений.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник