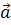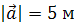Что такое положение точки

Положение точки на плоскости и в пространстве

Система координат — способ определять положение и перемещение точки или тела с помощью чисел или других символов. Координатами точки называется совокупность чисел, которые определяют ее положение в пространстве, на плоскости или на прямой.

Вообще систему координат можно выбрать на любой вкус — так, чтобы было удобно характеризовать положение в пространстве точек, образующих траекторию движения тела. Если эта траектория прямая, то для нее подходит линейная система координат — одна ось ОХ, где 0 — начало отсчета. Для движения точки на плоскости нужны две координатные оси. Их можно расположить под любым углом друг к другу. Если этот угол прямой, то мы имеем дело с обычной прямоугольной системой координат. Такие системы называют декартовыми в честь предложившего их французского математика и физика Рене Декарта. Координата точки на оси X называется абсциссой, координата на оси Y — ординатой, а координата на оси Z (если система строится в трехмерном пространстве) — аппликатой. Прямоугольную систему координат легко обобщить для пространства любой размерности, поэтому она широко применяется.

Есть также общая декартова система, которая не является прямоугольной.

Угол между координатными осями может отличаться от 90° — такую систему называют косоугольной. Ее применяют, например, для описания положения атомов в кристаллической решетке.

Для описания положения точек на плоскости может быть применена и двухосная система координат, где одна из осей вращается вокруг начала координат, все время указывая на изучаемую точку плоскости. Такая система координат называется полярной.

Существуют и сферические системы координат, определяющие положение точки на сфере. Например, географические координаты: широта, долгота и высота над определенной уровенной поверхностью (уровнем моря, к примеру).

Небесные координаты

В астрономии положение небесных тел определяется сферическими координатами, например прямым восхождением и склонением. Системы небесных координат отличаются отсчетной поверхностью — фундаментальной плоскостью и началом отсчета. Если это плоскость горизонта, то система называется горизонтальной, если экватора, то экваториальной, если эклиптики, то галактической.

Философ в печке

Рене Декарт, в честь которого названа система координат, в молодости служил в армии. Однажды в заброшенной деревне он, спасаясь от холода, забрался в печь и просидел там целый день. Когда вечером математик выбрался наружу, его философия, которую он позже описывал во многих работах, была уже готова. Декарт утверждал, что именно в печи ему пришли в голову знаменитые слова: «Мыслю, следовательно, существую».

Источник

Положение и движение точки в пространстве

Урок 2. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Положение и движение точки в пространстве»

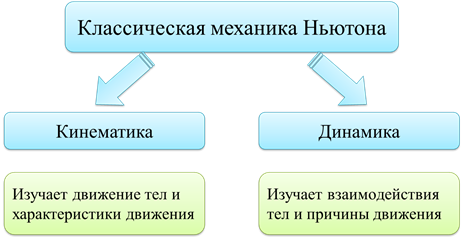
Мы продолжаем тему классической механики Ньютона. Механика делится на два основных раздела: кинематика и динамика. Мы начнём с изучения кинематики.

Кинематика изучает движение тел, способы описания этого движения, а также, его характеристики.

Описать движение человека или полет бабочки математически — это крайне сложная задача. Но есть задачи и проще: например, описать движение материальной точки. Добавим теперь, что эта точка двигается равномерно и прямолинейно. Тогда, описать её движение не так уж сложно. Именно с таких идеализированных моделей и следует начать изучение кинематики. Ведь если мы сможем описать движение каждой точки тела, то мы также сможем описать движение самого тела.

В первую очередь, нужно создать систему отсчёта. Система отсчёта состоит из тела отсчёта, системы координат и счётчика времени.

Тело отсчёта — это физическое тело, относительно которого задаётся положение данного тела или точки.

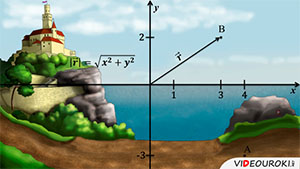
Понять это довольно просто. На рисунке изображено дерево.

На каком расстоянии находится это дерево? На каком расстоянии от чего? — спросите вы. Конечно, нам нужно выбрать точку отсчета. Это может быть белый треугольник на камне, а может быть флажок на за́мке. В зависимости от этого выбора, ответ на вопрос будет различным. Необходимо выбрать какую-то точку за точку отсчёта, то есть за ноль. Скажем, мы можем обозначить за ноль центр картинки.

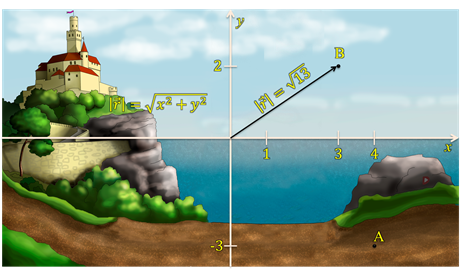
Далее, мы используем декартовы координаты, чтобы описать положения тел. Выбираем единичный отрезок и, исходя из этого определяем положения тел. Это положение задаётся с помощью координат. Например, точка А имеет координаты четыре и минус три, а точка Б — три и два. Также, можно задать положение тела с помощью радиус-вектора — это вектор, который соединяет точку и начало координат.

Радиус-вектор обозначается латинской буквой r и, как и любой другой вектор, имеет длину и направление. Длиной радиус-вектора будет является геометрическая сумма координат точки. Иными словами, мы вычисляем длину радиус-вектора, используя теорему Пифагора. То есть, длина радиус-вектора, описывающего положение точки B будет равна .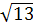

Модуль и направление любого вектора находят с помощью проекций этого вектора на оси координат.

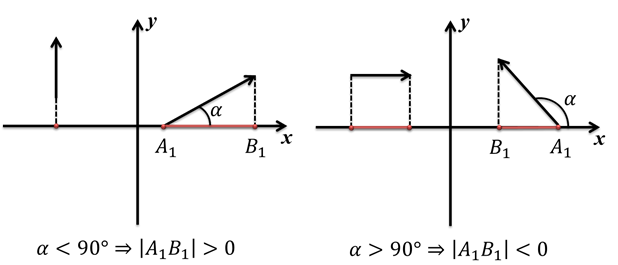
Что же такое проекция? Давайте рассмотрим вектор 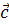с начальной точкой А и конечной точкой B, находящийся в системе координат на плоскости.

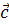
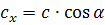
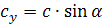
Из точек А и B опустим перпендикуляры на ось икс. Длина отрезка А₁ B₁ — это и есть проекция вектора цэ на ось x. Точно таким же способом находится проекция вектора на ось y. Как видно из построения: . Аналогично можно найти проекцию на ось y: ..

Проекция вектора на ось — это алгебраическая величина. Её знак можно определить так: если, двигаясь от начальной точки проекции до конечной точки проекции, надо идти в положительном направлении, то проекция положительная, а в противном случае — она отрицательная.

Иначе это можно объяснить так: если вектор составляет острый угол с направлением оси, на которую мы собираемся сделать проекцию, то проекция будет положительной, а если угол между вектором и направлением оси — тупой, то проекция будет отрицательной.

Нетрудно догадаться, что если вектор перпендикулярен оси, то его проекция на эту ось будет равна нулю.

Аналогично, если вектор параллелен оси, то его проекция на эту ось будет равна модулю вектора.

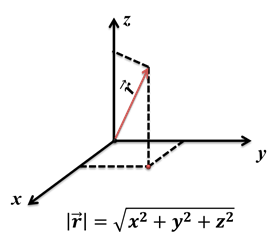
Рассмотрим теперь, как задать положение точки в пространстве, а не на плоскости. Как вы знаете, у есть три пространственных измерения, поэтому, чтобы задать положение точки в пространстве нам нужно три координаты. Сначала мы точно также, как и ранее, находим точку на плоскости, а потом от этой точки откладываем числовое значение координаты z параллельно оси Z.

Положение такой точки точно также можно задать с помощью радиус-вектора. Его модуль также будет находиться с помощью геометрической суммы координат точки.

Примеры решения задач.

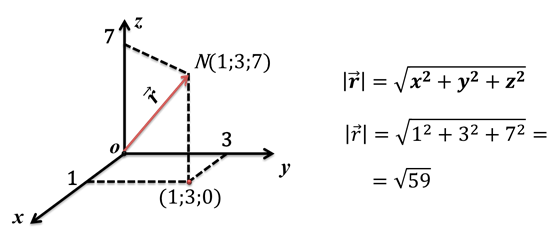
Задача 1. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

Задача 2. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

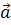
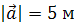
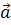
Задача 3. Постройте проекции вектора на оси x и y и найдите их числовые значения, если , а угол между и осью x составляет 30.

Источник

Кинематика. Задание положения точки.

Положение точки в пространстве можно задать двумя способами: координатным и векторным.

При задании движения координатным способом с телом отсчета связывают какую-либо систему координат, например, декартовую. Движение точки М будет задано в том случае, если ее координаты будут известны, как функции времени:

Эти зависимости называются уравнениями движения точки в декартовых координатах. Они выражают текущие координаты движущейся точки в виде функций времени. Если точка движется, оставаясь все время в одной плоскости, можно ограничиться двумя уравнениями движения: x = x(t), y = y(t).

Допустим, М – движущаяся точка относительно тела отсчета А. В теле А в качестве точки отсчета выберем произвольную точку О и построим вектор Этот вектор называется радиус-вектором точки М.

Радиус-вектор – это вектор, соединяющий начало отсчета с положением точки в любой момент времени.

Когда точка М движется, радиус-вектор непрерывно изменяется во времени, поэтому существует некоторая вектор-функция времени Зная эту функцию, для каждого времени t можно построить вектор и тем самым найти положение движущейся точки в данный момент. Функция называется векторным законом (векторным уравнением) движения точки М.

Точка задается радиус-вектором, если известны его длина (модуль) и направление в пространстве, другими словами – значения его проекций r_x, r_y, r_z на оси координат OX, OY и OZ, или углы между радиус-вектором и осями координат. При рассмотрении движения на плоскости:

Здесь за мы принимаем модуль радиус-вектора , а r_x и r_y являются его проекциями на оси координат, все три величины скалярны, x и y – координаты точки А.

Из этих уравнений видно, что между координатным и векторным способами задания положения точки существует связь.

Источник

Положение точки в пространстве

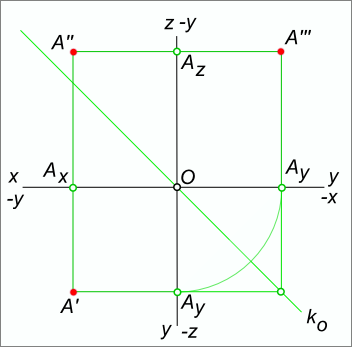
Положение точки в пространстве представим с помощью пространственного макета. Пусть даны в пространстве точка A и три взаимно перпендикулярные плоскости проекции.

Положение точки в пространстве определяется тремя координатами (x, y, z), показывающими величины расстояний, на которые она удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно через точку A провести прямые, перпендикулярные к плоскостям проекций, определить точки A`, A», A»` встречи этих прямых с плоскостями проекций и измерить величины отрезков [AA`], [AA»], [AA»`], которые укажут соответственно значение аппликаты z, ординаты y, абсциссы x точки A.

Прямые (AA` ⊥ H), (AA» ⊥ V), (AA»` ⊥ W) называют проецирующими прямыми или проецирующими лучами. Прямую (AA`), проецирующую точку A на горизонтальную плоскость проекций, называют горизонтально проецирующей прямой (лучом). Прямую (AA») проецирующую точку A на фронтальную плоскость проекций называют фронтально проецирующей прямой (лучом). Прямую (AA»`) проецирующую точку A на профильную плоскость проекций называют профильно-проецирующей прямой (лучом). Две проецирующие прямые, проходящие через точку A, определяют плоскость, которую принято называть проецирующей.

Связь между горизонтальной и профильной проекциями точки может быть установлена с помощью двух ортогональных отрезков [A`A<sub>y</sub>] и [A<sub>y</sub>A»`] и сопрягающей их дуги окружности, с центром в точке пересечения координатных осей. Отмеченной связью пользуются для нахождения недостающей профильной или горизонтальной проекции.

Положение профильной (горизонтальной) проекции по заданным горизонтальной (профильной) и фронтальной проекциям может быть найдено и без проведения дуги окружности. В этом случае связь между горизонтальной и профильной проекциями может быть установлена с помощью ломаной линии A`,A<sub>o</sub>,A»` с вершиной A_o на биссектрисе угла, образованного осями y. Биссектрису O,A_o,A»` называют постоянной прямой k_o эпюра Монжа.

Из записи следует: 1. Точка в пространстве удалена: а) от плоскости проекции W на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси y (или же фронтальная проекция A» от оси z); б) от плоскости проекции V на такую же величину, на какую горизонтальная проекция этой точки A` удалена от оси x (или ее профильная проекция A»` от оси z); в) от плоскости проекции H на такую же величину, на какую ее фронтальная проекция A» удалена от оси x (или ее профильная проекция A»` от оси y).

Если принять во внимание, что на эпюре прямые, перпендикулярные к осям проекций и соединяющие разноименные проекции точек, называют линиями связи (проекционной связи), то пункт 3. а) может быть сформулирован иначе: горизонтальная и фронтальная проекции любой точки принадлежат одной линии связи.

б) горизонтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси y; в) фронтальная и профильная проекции любой точки принадлежат одному перпендикуляру (одной линии связи) к оси z.

Источник

Положение и движение точки в пространстве

Урок 2. Физика 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Положение и движение точки в пространстве»

Мы продолжаем тему классической механики Ньютона. Механика делится на два основных раздела: кинематика и динамика. Мы начнём с изучения кинематики.

Кинематика изучает движение тел, способы описания этого движения, а также, его характеристики.

Описать движение человека или полет бабочки математически — это крайне сложная задача. Но есть задачи и проще: например, описать движение материальной точки. Добавим теперь, что эта точка двигается равномерно и прямолинейно. Тогда, описать её движение не так уж сложно. Именно с таких идеализированных моделей и следует начать изучение кинематики. Ведь если мы сможем описать движение каждой точки тела, то мы также сможем описать движение самого тела.

В первую очередь, нужно создать систему отсчёта. Система отсчёта состоит из тела отсчёта, системы координат и счётчика времени.

Тело отсчёта — это физическое тело, относительно которого задаётся положение данного тела или точки.

Понять это довольно просто. На рисунке изображено дерево.

На каком расстоянии находится это дерево? На каком расстоянии от чего? — спросите вы. Конечно, нам нужно выбрать точку отсчета. Это может быть белый треугольник на камне, а может быть флажок на за́мке. В зависимости от этого выбора, ответ на вопрос будет различным. Необходимо выбрать какую-то точку за точку отсчёта, то есть за ноль. Скажем, мы можем обозначить за ноль центр картинки.

Далее, мы используем декартовы координаты, чтобы описать положения тел. Выбираем единичный отрезок и, исходя из этого определяем положения тел. Это положение задаётся с помощью координат. Например, точка А имеет координаты четыре и минус три, а точка Б — три и два. Также, можно задать положение тела с помощью радиус-вектора — это вектор, который соединяет точку и начало координат.

Радиус-вектор обозначается латинской буквой r и, как и любой другой вектор, имеет длину и направление. Длиной радиус-вектора будет является геометрическая сумма координат точки. Иными словами, мы вычисляем длину радиус-вектора, используя теорему Пифагора. То есть, длина радиус-вектора, описывающего положение точки B будет равна .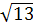

Модуль и направление любого вектора находят с помощью проекций этого вектора на оси координат.

Что же такое проекция? Давайте рассмотрим вектор 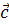с начальной точкой А и конечной точкой B, находящийся в системе координат на плоскости.

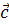
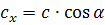
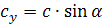
Из точек А и B опустим перпендикуляры на ось икс. Длина отрезка А₁ B₁ — это и есть проекция вектора цэ на ось x. Точно таким же способом находится проекция вектора на ось y. Как видно из построения: . Аналогично можно найти проекцию на ось y: ..

Проекция вектора на ось — это алгебраическая величина. Её знак можно определить так: если, двигаясь от начальной точки проекции до конечной точки проекции, надо идти в положительном направлении, то проекция положительная, а в противном случае — она отрицательная.

Иначе это можно объяснить так: если вектор составляет острый угол с направлением оси, на которую мы собираемся сделать проекцию, то проекция будет положительной, а если угол между вектором и направлением оси — тупой, то проекция будет отрицательной.

Нетрудно догадаться, что если вектор перпендикулярен оси, то его проекция на эту ось будет равна нулю.

Аналогично, если вектор параллелен оси, то его проекция на эту ось будет равна модулю вектора.

Рассмотрим теперь, как задать положение точки в пространстве, а не на плоскости. Как вы знаете, у есть три пространственных измерения, поэтому, чтобы задать положение точки в пространстве нам нужно три координаты. Сначала мы точно также, как и ранее, находим точку на плоскости, а потом от этой точки откладываем числовое значение координаты z параллельно оси Z.

Положение такой точки точно также можно задать с помощью радиус-вектора. Его модуль также будет находиться с помощью геометрической суммы координат точки.

Примеры решения задач.

Задача 1. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

Задача 2. В системе координат отметьте точку N (1;3;7), постройте соответствующий радиус-вектор и найдите его длину.

Задача 3. Постройте проекции вектора на оси x и y и найдите их числовые значения, если , а угол между и осью x составляет 30.

Источник