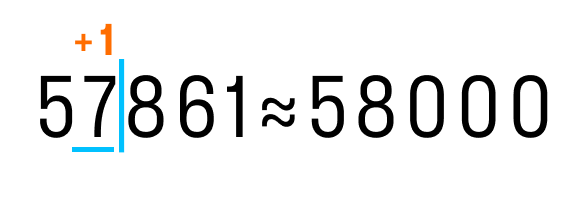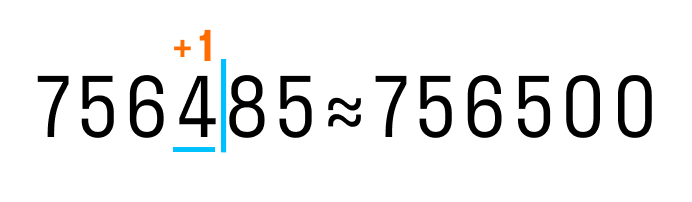Что такое после числа

Письмовник

Когда нужны буквенные наращения после цифр?

Техническое оформление текста

Когда применять наращения?

Наращение (буквенное падежное окончание) используется в записи порядковых числительных: 10-й класс «Б»; ученик 11-го класса; 1-й вагон из центра; 5-й уровень сложности; занять 2-е и 3-е места; в начале 90-х годов, 12-й маршрут.

Наращение не используется:

Как применять наращения?

Наращение падежного окончания в порядковых числительных, обозначенных арабскими цифрами, может быть однобуквенным или двухбуквенным.

По закрепившейся традиции наращение должно быть однобуквенным, если последней букве числительного предшествует гласный звук: 5-й день (пятый день), 25-я годовщина (двадцать пятая годовщина), в 32-м издании (в тридцать втором издании), в 14-м ряду (в четырнадцатом ряду).

Наращение должно быть двубуквенным, если последней букве предшествует согласный: 5-го дня (пятого дня), к 25-му студенту (к двадцать пятому студенту), из 32-го издания (из тридцать второго издания), из 14-го ряда (из четырнадцатого ряда).

Если подряд следуют два порядковых числительных, разделенных запятой или соединенных союзом, падежное окончание наращивают у каждого из них: 1-й, 2-й вагоны; 80-е и 90-е годы.

Если подряд следуют более двух порядковых числительных, разделенных запятой, точкой с запятой или соединенных союзом, то падежное окончание наращивают только у последнего числительного: 1, 2 и 3-й вагоны, 70, 80, 90-е годы.

Если два порядковых числительных следуют через тире, то падежное окончание наращивают:

а) только у второго числительного, если падежное окончание у обоих числительных одинаковое: 50–60-е годы, в 80–90-х годах;

б) у каждого числительного, если падежные окончания разные: в 11-м – 20-х рядах.

Как записать существительное или прилагательное, начинающееся числом? Как правильно: 3-х мерный или 3-мерный?

Корректное оформление: трехмерный (предпочтительно), 3-мерный.

Если в составе сложных существительных и прилагательных есть числительное, то его можно записать в словесной форме (прописью) или в словесно-цифровой форме (цифрой и присоединяемым дефисом существительным или прилагательным). При использовании словесно-цифровой формы записи буквенные наращения после числительных не пишутся.

Неверно

Верно

Примечание. В узкоспециальных изданиях допускается заменять прилагательное (название физической единицы) соответствующим кратким обозначением: 5-км расстояние, 12-т нагрузка.

Как писать названия классов: 1а класс или 1-й «А» класс?

Специальных правил оформления литеры в названии класса нет. В прочих случаях литерные добавления, как правило, пишутся строчными буквами без кавычек и присоединяются без пробела и без дефиса к предшествующей цифре: рисунок 1а, пункт 2д, дом 3а и т. д. Поэтому по аналогии можно было бы написать 1а класс, класс 10г, но на практике такой вариант не используется.

Наиболее распространены варианты оформления с прописной литерой, заключенной в кавычки: наш 10-й «Б», поступил в 1-й «А» класс и т. д. Такое оформление особенно уместно в тех случаях, когда литера располагается не сразу после числительного (или когда числительное вообще отсутствует): 10-й класс «Б»; классы «А» и «Б».

При написании числительного словом используется аналогичное оформление: первый «А» класс, десятый «Б». Ср.: Здесь можно было переждать какую-нибудь опасность, покурить, поговорить с девчонкой – словом, свой девятый «В» Мельников не случайно обнаружил именно здесь. Г. Полонский, Доживем до понедельника. Служкин запустил девятый «А» в кабинет и раскрыл классный журнал. А. Иванов, Географ глобус пропил.

Мильчин А. Э., Чельцова Л. К. Справочник издателя и автора. М., 2003.

Источник

Названия больших чисел

Существует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Числа состоят из цифр. Число 52 состоит из двух цифр: 5 и 2. Числа с 1 впереди и последующими нулями имеют названия. Всем известны: 10 — десять, 100 — сто, 1000 — тысяча, 1 000 000 — миллион. Так как большие числа с большим числом нулей записывать неудобно, используют сокращения в виде степеней: запись 10 11 означает число с 11-ю нулями, запись 10 52 означает число с 52-мя нулями и т.д. Приведем названия чисел с десятками и сотнями нулей.

Названия «круглых» чисел, которые можно встретить в школьной программе:
1 000 000 — миллион (6 нулей)
1 000 000 000 — миллиард или биллион (9 нулей)
1 000 000 000 000 — триллион (12 нулей)
1 000 000 000 000 000 — квадриллион (15 нулей)
1 000 000 000 000 000 000 — квинтиллион (18 нулей)
1 000 000 000 000 000 000 000 — секстиллион (21 нуль)
1 000 000 000 000 000 000 000 000 — септиллион (24 нуля)
1 000 000 000 000 000 000 000 000 000 — октиллион (27 нулей)
1 000 000 000 000 000 000 000 000 000 000 — нониллион (30 нулей)
1 000 000 000 000 000 000 000 000 000 000 000 — дециллион (33 нуля)

Еще некоторые примеры интересных названий:
10 100 — гугол, googol (100 нулей)
10 10 100 — гуголплекс, googolplex (десять в степени гугол)
10 140 — асанкхейя, asankhyeya или сто квинквадрагинтиллионов
10 303 — центиллион, centillion
10 3003 — миллиллион, millillion
10 3000003 — милли-миллиллион, milli-millillion

Самого большого числа в мире не существует, так как любое большое число всегда можно увеличить, умножить, возвести в степень, и получится другое большее число. Бесконечность не является числом.

Из известных самых больших чисел, имеющих название (математическое доказательство) можно выделить: число TREE(3), число SCG(13), число Лоудера, число Мозера, число Скьюза, число Райо, число Грэма, инфитеиплеон.

Таблица больших чисел с указанием количества нулей и названиями на русском и английском.

Источник

Включается ли в период времени дата после предлогов «до» и «по»

Если в договоре для определения срока используется предлог «по», то дата после него включается в соответствующий срок. Эта позиция обусловлена тем, что при толковании условий договора суд принимает во внимание буквальное значение содержащихся в нем слов и выражений ( ч. 1 ст. 401 ГК). А по словарю русского языка С.И. Ожегова предлог «по» имеет несколько значений, в том числе указывает на меру времени или срок. Другими словами, предлог «по» перед датой подразумевает «включая эту дату».

Пример
В договоре указано, что товар должен быть оплачен в срок по 25.01.2021. В таком случае последний день для оплаты товара — 25.01.2021.
Стороны согласовали срок действия договора с 01.01.2021 по 28.02.2021. В этой ситуации последний день действия договора — 28.02.2021.

По поводу предлога «до» отсутствует единое мнение.

Одни считают, что использование предлога «до» исключает указанную после него дату из срока. Например, если указано «до 10.02.2021», то срок оканчивается 09.02.2021 в 24 часа 00 минут. Объясняется это тем, что по словарю русского языка С.И. Ожегова предлог «до» употребляется для указания на время, отделяющее одно событие от другого.

Вместе с тем есть и противоположная точка зрения — предлог «до» не исключает указанную после него дату из срока. Так, если указано «до 10.02.2021», то последний день срока — 10.02.2021. Такой позиции, например, придерживался ВХС в письме от 03.06.2005 N 03-24/1053.

На заметку
В Инструкции по делопроизводству установлено правило касательно предлога «до». Так, если срок исполнения документа определяется с использованием предлога «до», указанная за ним дата является крайней датой исполнения документа (подп. 146.4 п. 146). Однако Инструкция по делопроизводству устанавливает общие требования к документированию управленческой деятельности и организации работы с документами, т.е. не содержит требований к договорам (п. 1).

Следовательно, если в договоре для определения срока использован предлог «до», то может возникнуть спор.

Суд в таком случае будет устанавливать конечную дату срока путем сопоставления условия о сроке с другими условиями и смыслом договора в целом. Если это не поможет определить момент окончания срока, то суд будет выяснять действительную общую волю сторон с учетом цели договора. При этом будут приниматься во внимание все соответствующие обстоятельства, включая предшествующие договору переговоры и переписку, практику, установившуюся во взаимных отношениях сторон, последующее поведение сторон (ст. 401 ГК).

Во избежание споров рекомендуем добавлять слово «включительно» после указания даты. Это целесообразно делать как при использовании предлога «до», так и с предлогом «по». Также избежать разной трактовки срока можно, если использовать конструкцию «не позднее…».

Примеры формулировок в договоре
«Срок оплаты работ — до 10.02.2021 включительно.»
«Срок действия настоящего договора с 01.01.2021 по 20.03.2021 включительно.»
«Товар по настоящему договору должен быть поставлен не позднее 29.01.2021.»

Читайте этот материал в ilex >>*
*по ссылке Вы попадете в платный контент сервиса ilex

Источник

Разряды и классы чисел

Числа и цифры

Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.

Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.

Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …

От количества цифр в числе зависит его название.

Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.

Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.

Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.

Каждая цифра в записи многозначного числа занимает определенное место — позицию.

Классы чисел

Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.

Названия классов многозначных чисел справа налево:

Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:

А теперь прочитаем число единиц каждого класса слева направо:

Разряды чисел

От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:

Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.

Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.

У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.

Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.

Низший (младший) разряд многозначного натурального числа — разряд единиц.

Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.

Разрядные единицы обозначают так:

Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.

Чтобы легче понимать математику — записывайтесь на наши курсы по математике!

Потренируемся

Пример 1. Записать цифрами число, в котором содержится:

Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:

Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.

Пример 2. Сколько сотен содержится в числе 6284?

В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.

Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.

Значит, в данном числе содержится 62 сотни.

Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.

Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:

Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.

Источник

Правильное округление чисел

Приближенные значения

В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.

У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Примерчики

Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.

Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.

Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.

Приближенное значение — число, которое получилось после округления.

Для записи результата округления используют знак «приблизительно равно» — ≈.

Округлить можно любое число — для всех чисел работают одни и те же правила.

Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.

Округление натуральных чисел

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.

Особенности натуральных чисел:

Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.

Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.

Правила округления чисел:

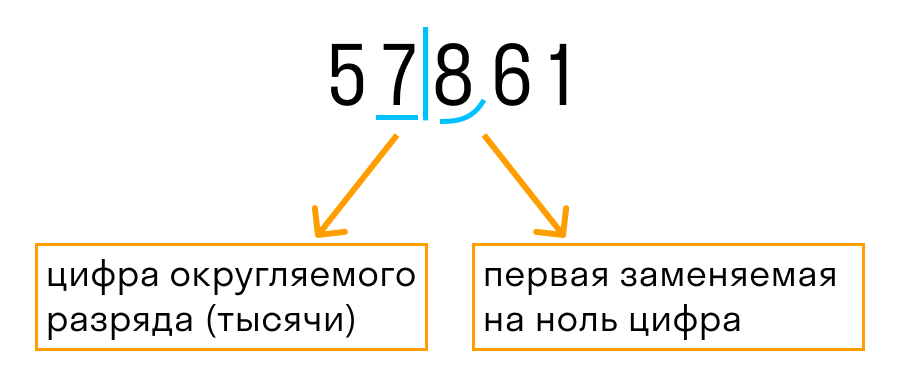
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.

После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.

Теперь округлим 756 485 до сотен:

Округлим число 123 до десятков: 123 ≈ 120.

Округлим число 3581 до сотен: 3581 ≈ 3580.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.

Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:

Округление десятичных дробей

Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:

Разряды целой части:

Разряды дробной части:

Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.

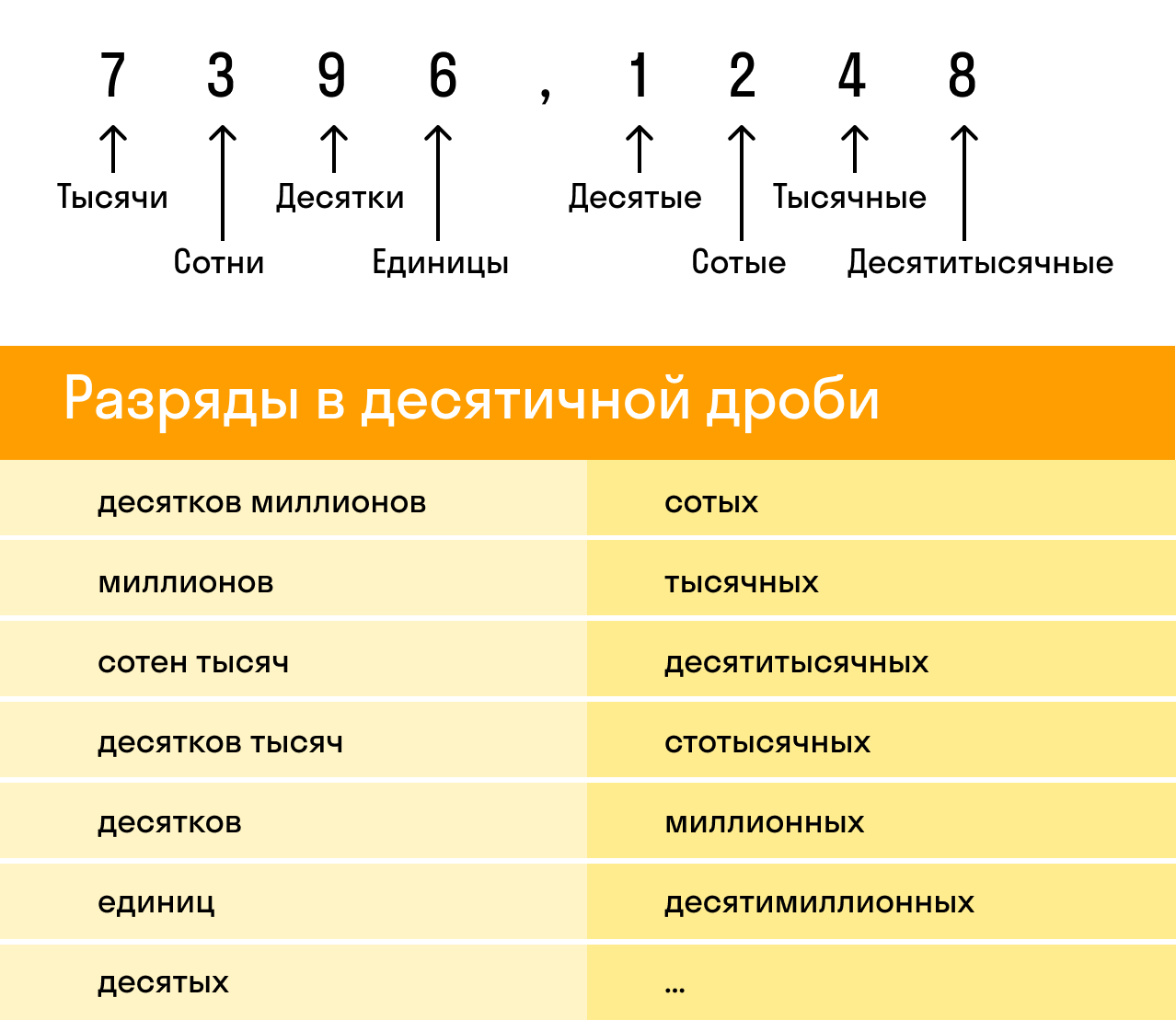
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:

Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.

То число, к которому дробь ближе, называют округленным значением числа.

Цифра, которая записана в данном разряде:

Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.

Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.

Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.

Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.

Пример 1

256,43 ≈ 256,4 — округление до десятых;

4,578 ≈ 4,58 — округление до сотых;

17,935 ≈ 18 — округление до целых.

Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.

Пример 2

79,7 ≈ 80 — округление до десятков;

0,099 ≈ 0,10 — округление до сотых.

Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.

Источник