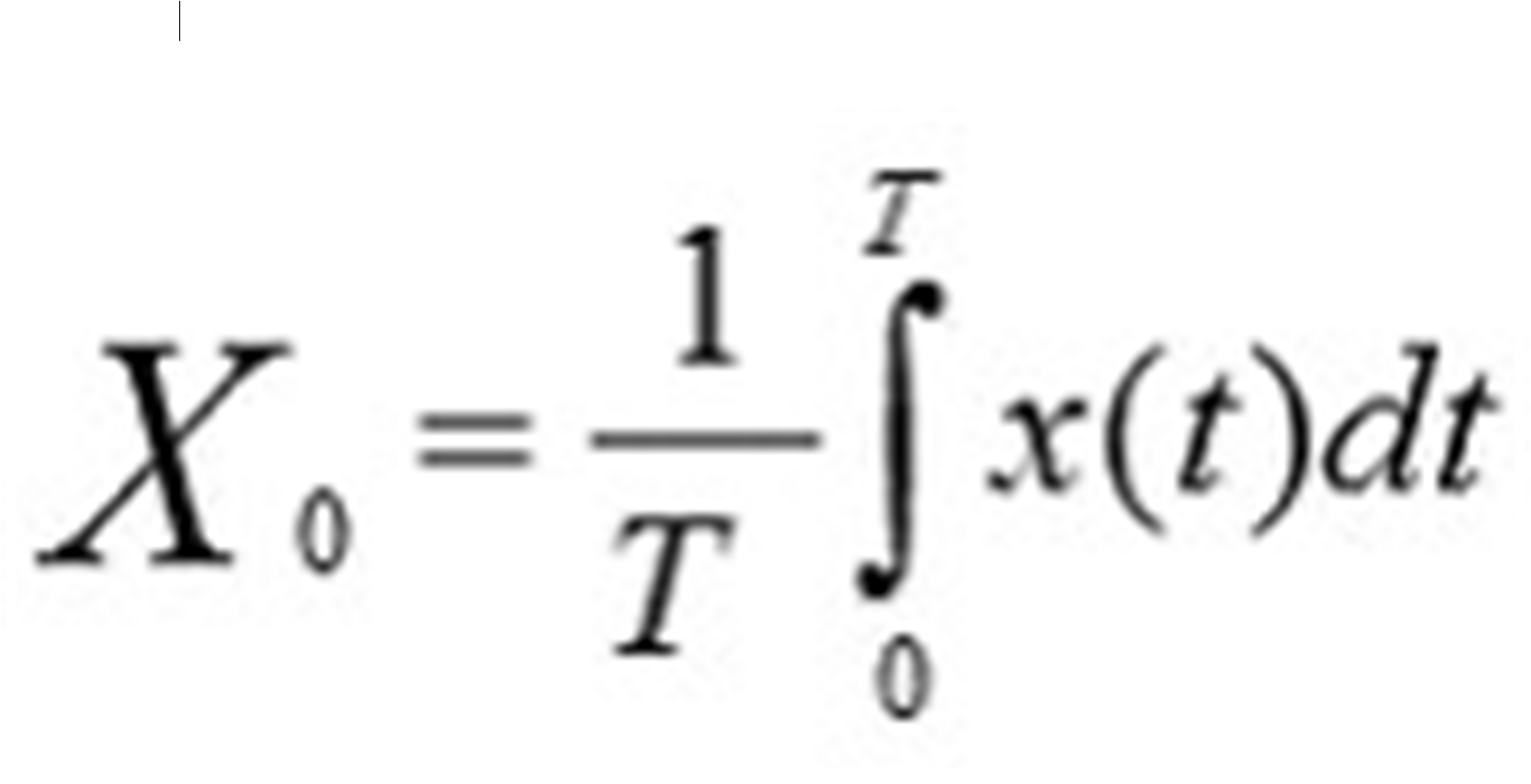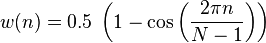Что такое постоянная составляющая сигнала

Постоянная составляющая сигнала изображения

Свет по своей природе униполярен, так как яркость не может быть величиной отрицательной. Следовательно, и сигнал изображе­ния также униполярен и поэтому имеет среднюю (постоянную) со­ставляющую.

Среднее значение сигнала за строку пропорционально средней яркости этой строки. Среднее значение сигнала за полный кадр пропорционально средней яркости всего изображения.

Рис. 4.5. Зависимость средней составляющей от характера изображения для сигналов: а — негативного; б — позитивного

Средняя составляющая зависит, во-первых, от характера объек­та (соотношения площадей его ярких и темных элементов) и, во-вторых, от освещенности объекта. На рис. 4.5 показано образова­ние средней составляющей для двух изображений, А и Б при негативном и позитивном сигналах.

В изображении А преобладают темные участки, так как это уз­кая светлая полоска на темном фоне. В изображении Б, нао­борот, преобладают светлые участки.

Из рисунка видно, что при негативной полярности сигнала для изображения А средняя составляющая значительно больше, чем для изображения Б. При позитивной полярности сигнала, наоборот, средняя составляющая изображения Б больше, чем для изображе­ния А. Если объект подсветить, то черные элементы станут се­рыми и средняя составляющая негативного сигнала уменьшится, а позитивного — увеличится. Если освещение объекта ослабить, то средняя составляющая негативного сигнала возрастет, а позитив­ного — уменьшится.

При передаче изображения неподвижного объекта и неизмен­ной освещенности средняя составляющая будет постоянной. Обычно во время телевизионной передачи освещенность и содержание изо­бражения (т. е. соотношение между светлыми и темными элемен­тами) меняются. Однако эти процессы происходят постепенно. По­этому частота изменений средней составляющей получается очень низкой и колеблется в пределах от 0 до 2. 3 Гц, что дает право по сравнению даже с самой низкой частотой сигнала изображе­ния (50 Гц) во всех случаях считать среднюю составляющую по­стоянной составляющей сигнала.

В усилительных ступенях, имеющих разделительные конденсато­ры, постоянная составляющая неизбежно теряется. При этом лю­бая сцена, независимо от ее содержания и освещенности, вос­производится на экране кинескопа с одинаковой средней яркостью, а хорошо освещенные кадры не отличаются от затемненных. В цвет­ном телевидении потеря постоянной составляющей приводит к ис­кажению насыщенности цветов изображения по всему полю экрана:

недостаток средней яркости воспринимается как сгущение красок, а ее избыток, наоборот, как обеднение. Для устранения искаже­ний, возникающих вследствие потери постоянной составляющей, в телевизионных устройствах принимаются меры по ее сохранению или восстановлению.

4.7. Качество телевизионного изображения

Качество изображения, воспроизводимого на экране кинескопа, определяется степенью соответствия его изображению передаваемо­го объекта и, в первую очередь, зависит от особенностей форми­рования сигнала изображения и вносимых в него искажений.

На рис. 4.6, а, б показаны изображение, состоящее из чередую­щихся разнояркостных деталей различной ширины, и форма не­гативного сигнала одной строки развертки. Пока электронный луч ЭЛ перемещается по достаточно широкой светлой детали А, об­разуется сигнал изображения, соответствующий уровню белого. Ко­гда луч достигает левой границы темной детали Б и проходит ее, сигнал постепенно нарастает от уровня белого до уровня черного, а затем, при прохождении правой границы этой детали, посте­пенно спадает снова до уровня белого.

Аналогично формируются сигналы и при развертке других де­талей изображения (В, Г, Д и т.д.). Однако по мере уменьше­ния их размеров уменьшаются амплитуда и период следования соответствующих импульсов. Так, импульсы, соответствующие круп­ным деталям изображения (А, Б, В), ширина которых больше диаметра электронного луча на поверхности фотомишени, достигают полного размаха (от уровня белого до уровня черного) и имеют большой период следования, т. е. являются низкочастотными. Им­пульсы, соответствующие мелким, соизмеримым с диаметром луча деталям (Г, Д, Е, Ж, 3, И), образуют высокочастотные состав­ляющие сигнала изображения. Амплитуда этих импульсов убывает по мере уменьшения размеров деталей, принимая практически нулевые значения для деталей, ширина которых меньше половины диаметра луча (К, Л, М). Это значит, что сигнал изображения на участке строки от И до Н приобретает почти постоянное значение, соответствующее средней яркости данного участка, а детали К, Л, М раздельно не передаются и не будут воспроизведены.

Таким образом, вследствие конечных размеров диаметра луча ог­раничивается разрешающая способность телевизионной системы, т. е. ее способность передавать и воспроизводить относительно мелкие детали изображения. По той же причине форма импульсного сигнала получается отличной от прямоугольной, и границы между де­талями изображения различной яркости на экране кинескопа ока­зываются размытыми. Однако при оптимальной фокусировке и боль­шой скорости движения электронного луча, а также неискажен­ной передаче сигнала изображения указанные дефекты практичес­ки незаметны.

Если же форма сигнала изображения, поступающего на моду­лятор кинескопа, искажена, то качество изображения заметно ухуд­шается. Так, ослабление («завал») низкочастотных (или среднечастотных) составляющих (рис. 4.6, б, штриховая кривая 1) приводит к появлению убывающего по яркости серого тянущегося про­должения («тянучки») справа от границы крупной темной детали Б (рис. 4.6, в). Ослабление высокочастотных импульсов (штриховая кривая 3) вызывает уменьшение четкости изображения, так как яр­кость мелких деталей Е, Ж, 3 при этом усредняется (рис. 4.6,г). Если, наоборот, имеет место чрезмерное усиление высокочастотных составляющих сигнала (штриховая кривая 2), то наблюдается де­фект, называемый «пластикой», т. е. справа от границы раздела между темной и светлой деталями Г и Д появляется более свет­лая (белее белого) окантовка (рис. 4.6, д).

Рис. 4.6. Зависимость качества изображения от формы сигнала изображения:

а — передаваемое изображение; б — форма негативного сигнала одной строки раз­вертки; в — искажения изображения при завале низкочастотных или среднечастотных составляющих сигнала («тянучка»); г—искажения изображения при ослаб­лении высокочастотных импульсов (потеря четкости изображения): д—искажения изображения при чрезмерном усилении высокочастотных составляющих сигнала («пластика»)

Для устранения рассмотренных недостатков в телевизионных усилительных устройствах широко применяются схемы низкочастотной и высокочастотной коррекции амплитудно-частотных характеристик.

Источник

Что такое постоянная составляющая сигнала

Компьютерная техника, радиоэлектроника, электрика

Переменный ток

Переменный ток все время изменяет свое направление в отличие от постоянного, который протекает только в одном направлении. Постоянный ток вырабатывают батареи и источники постоянного тока, а переменный – генераторы сигналов и государственные энергетические системы.

Синусоидальные колебания

Форма переменного тока или напряжения может принимать самые различные виды. Наиболее распространенной является синусоидальная форма переменного напряжения или тока (рис. 2.1). Синусоидальное колебание имеет два максимальных значения, или пика: положительный пик и отрицательный. Пиковое значение называется также амплитуде синусоиды. Значение синусоидального напряжения, измеренное от пика до пика (размах), является разностью потенциалов между положительным пиком и отрицательным.
Размах = Положительная амплитуда + Отрицательная амплитуда = Удвоенная амплитуда.

Рис. 2.1. Синусоидальные колебания переменного тока

Среднеквадратическое значение

Постоянный ток имеет постоянное значение, и это значение можно использовать во всех вычислениях. Значение же переменного тока изменяется во времени. Чтобы преодолеть эту трудность, за «постоянное» значение переменного тока приняли и используют его среднеквадратическое значение.
Среднеквадратическое значение переменного тока является эквивалентом значения постоянного тока, при котором вырабатывается такая же мощность, что и при исходном значении переменного тока. Если известно среднеквадратическое значение переменного тока, то его можно использовать для вычисления мощности так же, как если бы это было постоянное напряжение или ток. Например:

Мощность пост. тока = Постоянный ток х Постоянное напряжение;
Мощность перем. Тока = Среднеквадр. значение тока х Среднеквадр. значение напряжения.

Значения переменного тока и напряжения всегда задают в виде среднеквадратической величины, за исключением специально оговоренных случаев.
Пример 1
Какое сопротивление имеет домашний электрический обогреватель мощностью 1 кВт?
Решение
Домашние обогреватели работают от сетевого напряжения, имеющего среднеквадратическое значение 240 В (в России 220 В. — Прим. перев.). Мощность, потребляемая обогревателем, составляет 1 кВт = 1000 Вт. Из формулы P = V2/R определяем

P = V2/R = 240*240/1000 = 57, б Ом.

Соотношение между пиковыми и среднеквадратическими значениями

Среднеквадратическое значение сигнала переменного тока зависит от его формы. Так, среднеквадратическое значение синусоидального сигнала составляет 0,707 его пикового значения (амплитуды). Заметим, что это справедливо только для синусоидального сигнала. Например, если амплитуда синусоидального сигнала Vр = 10 В, то его среднеквадратическое значение составит Vср.кв. = 0,707 * Vр = 0,707 * 10 = 7,07 В (см. рис. 2.2). Из соотношения Vср.кв. = 0,707 * Vр следует, что

Vр = 1/0,707 * Vср.кв. = 1,414 * Vср.кв.

Рис. 2.2. Среднеквадратическое значение синусоидального сигнала.

Рис. 2.3. Постоянная составляющая сигнала переменного тока.

Постоянная составляющая в сигнале переменного тока

До сих пор мы имели дело с сигналами переменного тока, которые не содержали постоянной составляющей. Рассмотрим два синусоидальных сигнала, изображенных на рис. 2.3. Левый сигнал не имеет постоянной составляющей, и его положительный пик равен отрицательному. Правый же сигнал содержит составляющую постоянного тока величиной 5 В.
Постоянная составляющая переменного тока называется также средним, или усредненным значением сигнала переменного тока.
Определим постоянную составляющую сигнала, имеющего прямоугольную форму (рис. 2.4).

Рис. 2.4.

1. Сначала определим положение нулевого уровня.
2. Вычислим площадь А1, лежащую выше нулевого уровня:
А1 = 4*1 = 4.

3. Вычислим площадь А2, лежащую ниже нулевого уровня:
А2 = 2*1 = 2.

4. Вычислим суммарную площадь:
А1 – А2 = 4 – 2 = 2.

5. Отсюда среднее значение напряжения за период равно
Суммарная площадь/Время периода = 2/3 = 0,67 В.

Среднеквадратическое значение сложных сигналов

Как уже говорилось, соотношение
Среднеквадратическое значение = 0,707 амплитуды
справедливо только для синусоидальных сигналов. Среднеквадратическое значение сигналов, имеющих другую форму, может быть определено следующим образом.
1. Определить площадь сигнала за один период. Заметим, что при определении площади отрицательное значение превращается в положительное.
2. Определить среднее значение площади сигнала за период.
3. Вычислить квадратный корень из средней площади сигнала за период.
Определим среднеквадратическое значение сигнала, имеющего форму меандра (рис. 2.5(а)). Площадь положительного полупериода этого сигнала равна 3 * 3 = 9. Площадь отрицательного полупериода составля¬ет (-3) * (-3) = 9. Среднее значение площади за период, следовательно, равно 9. Отсюда среднеквадратическое значение напряжения будет корень из 9 = 3 В.

Рис. 2.5. Сравнение среднеквадратических значений
прямоугольного и синусоидального сигналов.

Для сравнения определим среднеквадратическое значение синусоидального напряжения, имеющего значение положительной и отрицательной амплитуды +3 В и –3 В соответственно (рис. 2.5(б)): 0,707 * 3 В = 2,12 В.

Как видим, прямоугольный сигнал имеет большее среднеквадратическое значение. Это объясняется тем, что площадь под прямоугольной огибающей больше, чем площадь под синусоидой, хотя оба сигнала имеют одинаковые значения положительного и отрицательного пиков. В данном случае среднеквадратическое значение прямоугольного сигнала равно его пиковому значению.

На рис. 2.6 изображен прямоугольный сигнал, имеющий только положительные значения. Среднеквадратическое значение этого сигнала меньше его пикового значения.
При однополупериодном выпрямлении среднеквадратическое значение напряжения равно половине его амплитуды.
При двухполупериодном выпрямлении среднеквадратическое значение такое же, как у полной синусоиды, т. е. 0,707 амплитуды (рис. 2.7), поскольку при вычислении среднеквадратического значения положительная полуволна сигнала идентична отрицательной, положительный полупериод идентичен отрицательному.
Заметим, что постоянная составляющая, или среднее значение сигнала, это просто усредненное значение напряжения за один период, не имеющее никакого отношения к среднеквадратическому значению.

Рис. 2.6. Среднеквадратическое значение прямоугольного сигнала, имеющего только положительную полярность.

Рис. 2.7. (а) При однополупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,5 амплитуды.
(б) При двухполупериодном выпрямлении синусоидального напряжения его среднеквадратическое значение равно 0,707 амплитуды.

В этом видео наглядно рассказывается о типах тока, в том числе о переменном токе:

Источник

Термин: Постоянная составляющая сигнала

Значение постоянной составляющей сигнала – это среднее значение этого сигнала на рассматриваемом промежутке времени. Теоретически постоянная составляющая сигнала вычисляется интегральным выражением

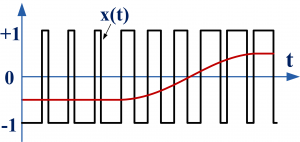
где интервал времени T стремится к бесконечности. При практической интерпретации этого понятия в задачах обработки сигнала интеграл берётся на скользящем интервале времени заданного размера (т.е. по выборке изучаемого участка сигнала). Постоянная составляющая сигнала, исходя из геометрического смысла интеграла, хорошо видна на графике сигнала во времени как величина, равная площади между осью нулевого значения сигнала и графиком (учитывая, что под осью площадь отрицательна, а над осью – положительна). На графике показано красной кривой значение постоянной составляющей X₀ для скользящего окна интегрирования с размером, сравнимым с периодом сигнала.

Для цифрового сигнала оценка постоянной составляющей – это среднее арифметическое выборки из N отсчетов.

В спектральном представлении сигнала информацию о постоянной составляющей сигнала несёт нулевая гармоника спектра этого сигнала.

Размер выборки для вычисления постоянной составляющей зависит от условий задачи. Например, если сигнал имеет выраженные гармонические составляющие с известной частотой, то целесообразно, чтобы выборка включала целое число периодов этих составляющих (иначе на выходе будут пульсации). Если спектр сигнала не известен заранее, можно применить оконную функцию – например, окно Ханна:

Это позволяет уменьшить влияние нецелых периодов на концах выборки. Примеры оконных функций можно найти, например, здесь.

На практике, когда сигналы представлены напряжением или током, для обозначения режима измерения постоянного напряжения или тока, который по сути является режимами измерения постоянной составляющей этих сигналов, широко применяется термин DC (direct current).

Не во всех сигналах постоянная составляющая информационна. Для удаления постоянной составляющей из сигнала применяют фильтры высокой частоты.

Некоторые среды передачи сигнала не позволяют передавать постоянную составляющую сигнала (например, среды, имеющие емкостную или индуктивую гальваническую развязку), Для передачи постоянной составляющей сигнала через такие среды используют различные технические принципы, связанные со специальными способами модуляции и кодирования сигнала.

Постоянная составляющая может быть и не связана с сигналом, а порождаться самим прибором или преобразователем (из-за неидельности его характеристик) в виде смещения нуля.

Источник

Эта непостоянная постоянная составляющая: что делать?

Analog Devices AD822

Владимир Рентюк, Запорожье, Украина

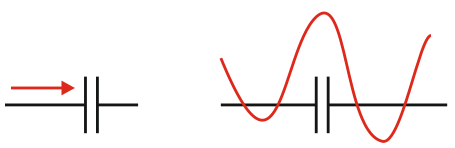
Ситуация, когда в полезном сигнале имеется постоянная составляющая, достаточно обычна. Эта составляющая может быть представлена некоторым фиксированным смещением или иметь нестационарный, плавающий характер. Как правило, она является паразитной и мешает производить обработку полезного переменного сигнала. Таким образом, возникает необходимость ее устранения, и обычно для этого используется разделительный конденсатор. Безусловно, это самое распространенное решение, и сразу вспоминается шутка, которой маститые инженеры вводят в ступор новичков, задавая им простой вопрос: как быстро доказать, что конденсатор проводит переменный ток и не пропускает постоянный. И на все их долгие и пространные объяснения показывают свое (Рисунок 1).

а) б)
Рисунок 1.	Конденсатор для напряжения постоянного и переменного токов. Постоянный ток «уперся» в конденсатор и дальше пройти не может (а), а переменный его «обходит» (б).

Если все изложенное является критичным, то на первый план выходит компенсация постоянной составляющей внешним смещением или задание строго необходимого при наличии некоторой постоянной составляющей в структуре сигнала. Подход хороший, но только если точно известно, какая она (постоянная составляющая) будет, и будет ли она постоянной. Причем, не только во времени, а и, в зависимости от внешних условий, как минимум, от температуры. Если не будет точной компенсации, то в случае, например, измерения среднеквадратичного значения сигнала, будет допущена ошибка. Еще один момент кроется в том, что если аналоговая часть, допустим некоторый масштабирующий усилитель, подключается на вход АЦП микроконтроллера, то для получения максимального динамического диапазона необходимо поднять аналоговый сигнал на величину напряжения, равную половине напряжения питания микроконтроллера или половине максимального номинального напряжения, допустимого для входа его АЦП.

Автору статьи пришлось однажды искать решение для, скажем так, «изделия специального назначения». В нем был блок обработки сигналов с большим динамическим диапазоном, поступающих с некого сенсора через систему сложных, переключаемых в зависимости от ситуации фильтров. Причем спектр этого сигнала достаточно широк, а его низкочастотная составляющая могла лежать в области инфранизких частот. Вычислитель осуществлял контроль среднеквадратичного уровня сигнала и при его отклонении в пределах ±1% выдавал некую очень важную команду. Кроме переменной составляющей, входной сигнал в своей структуре содержал еще и неизвестное по величине и меняющееся по уровню постоянное напряжение смещения. Вдобавок, на печатной плате не было лишнего места, и даже ее высота была ограничена, Ну и, коль это было «изделие специального назначения», то и требования к нему по ударо- и вибростойкости были специальные. Как видим, ни о каких разделительных конденсаторах или о подаче компенсирующего смещения речь даже не могла идти. Схемное решение, которое решило проблему такой необычной компенсации постоянной составляющей исходного сигнала (без разделительного конденсатора) и задания фиксированного и строго определенного смещения, приведено на Рисунке 2. Впервые в общем виде оно было опубликовано в [1].

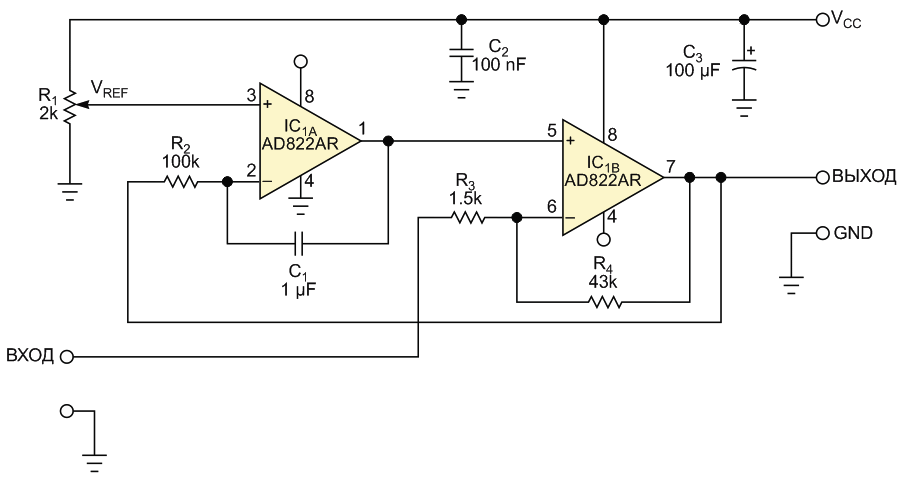Рисунок 2.	Схема цепи ультразвукового сенсора, использующая компенсацию постоянной составляющей входного сигнала [1].

Для предлагаемой схемы желательно использовать операционный усилитель (ОУ) типа «rail-to-rail» по входу и выходу, естественно, допускающий включение в режиме с однополярным источником питания, например, AD822 [2]. Это увеличивает динамический диапазон компенсации постоянной составляющей входного напряжения. Заданная величина выходного смещения, не зависящая от величины постоянной составляющей в структуре сигнала, устанавливается подачей необходимого уровня опорного напряжения V_REF. На Рисунке 2 он формируется при помощи построечного резистора R₁, но этот резистор может быть заменен источником опорного напряжения или резистивным делителем. (Автором успешно использовались оба варианта). Как уже отмечалось выше, для получения максимального динамического диапазона выходной уровень опорного постоянного напряжения устанавливается равным половине напряжения питания V_CC. Усилитель, выполненный на ОУ IC_1B, усиливает и инвертирует высокочастотную составляющую напряжения входного сигнала с коэффициентом усиления равным R₄/R₃, обычным для схем усилителей на базе ОУ в инвертирующем включении.

Инвертирующий вычитающий интегратор, выполненный на ОУ IC_1A, обеспечивает компенсацию любого неподходящего для работы схемы напряжения смещения внутри контура отрицательной обратной связи. Переменная составляющая сигнала ослабляется выбором соответствующей постоянной времени интегратора R₂C₁, оставляя, таким образом, лишь усредненную постоянную составляющую смещения на выходе ОУ IC_1B ниже нижней граничной рабочей частоты входного сигнала. Это смещение выходного сигнала в рабочем диапазоне частот будет равно заданному уровню опорного напряжения. На Рисунке 2 показана временная диаграмма действия такой компенсации для случая ступенчатого изменения смещения постоянной составляющей во входном сигнале на величину 4 В. То есть, если учитывать коэффициент усиления схемы, приведенной на Рисунке 2, равный

это будет в условиях очень глубокого перерегулирования, как минимум в 29 дБ! Тем не менее, и это можно видеть из Рисунка 3, время установления предлагаемой схемы с учетом переходных процессов составляет менее 100 мс.

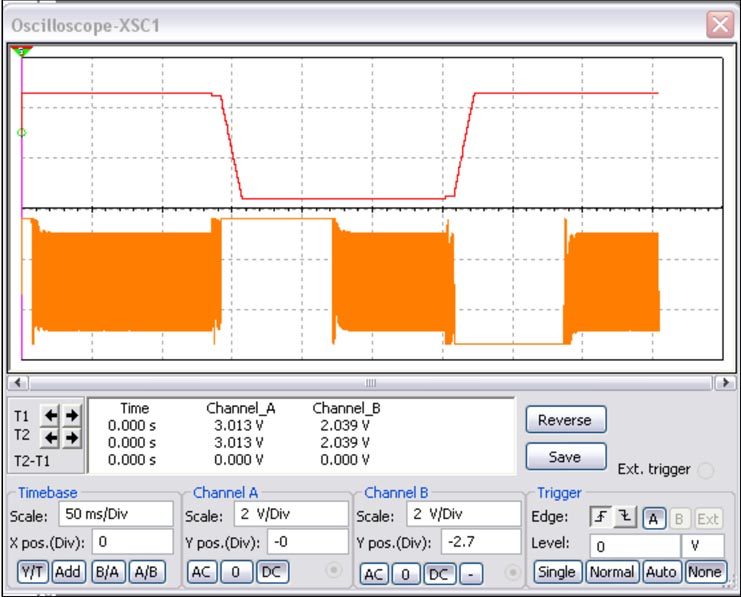Рисунок 3.	Процесс компенсации ступеньки смещения входного напряжения в 4 В. Время установления менее 100 мс.

Рассмотренное схемотехническое решение имеет еще две дополнительные полезные области применения. Во-первых, это ФВЧ первого порядка без входных емкостей, в котором амплитудно-частотная характеристика имеет спад 6 дБ/октава с частотой среза по уровню –3 дБ. Во-вторых, эта схема также может служить удобным в использовании дифференциатором (инвертирующим и без входного конденсатора) с реакцией на шаг ступенчатого изменения входного напряжения. Как известно, такие дифференциаторы являются потенциально неустойчивыми и, следственно, не очень удобны в применении.

Нижняя частота среза схемы, приведенной на Рисунке 2, определяется по формуле:

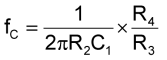(1)

Формула получена в результате моделирования. Для значений элементов, приведенных на Рисунке 2, частота среза в области низких частот равна 47 Гц.

А где же обещанные инфранизкие частоты, спросит читатель? Заменим элементы в интеграторе на R₂ = 2 МОм и C₁ = 2.2 мкФ и зададим коэффициент усиления, например, равный 12, то есть k = R₄/R₃ = 12. Это будет соответствовать той задаче, которую решал автор статьи в своем, упомянутом в начале статьи, проекте.

Согласно формуле (1), имеем:

АЧХ такого варианта каскада приведена на Рисунке 4.

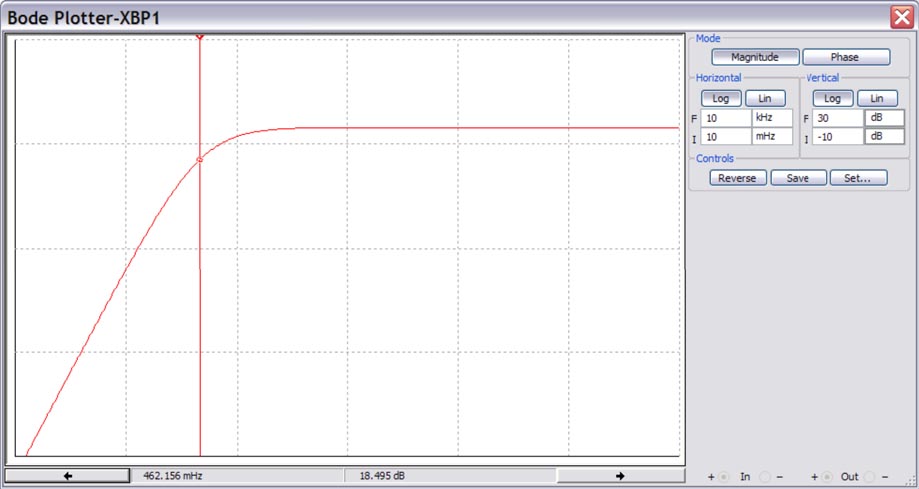Рисунок 4.	Амплитудно-частотная характеристика в области инфранизких частот.

Как видим, все обошлось без нежелательного разделительного электролитического конденсатора. В противном случае пришлось бы использовать электролитический конденсатор емкостью, как минимум, в 470 мкФ и, естественно, схему формирования сдвига выходного напряжения. Приведенное схемное решение было использовано автором в целом ряде проектов и ни разу не имело нареканий.

Ссылки:

Источник