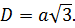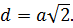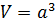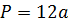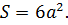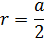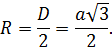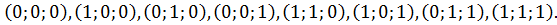Что такое поверхность куба в математике
Что такое куб: определение, свойства, формулы
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
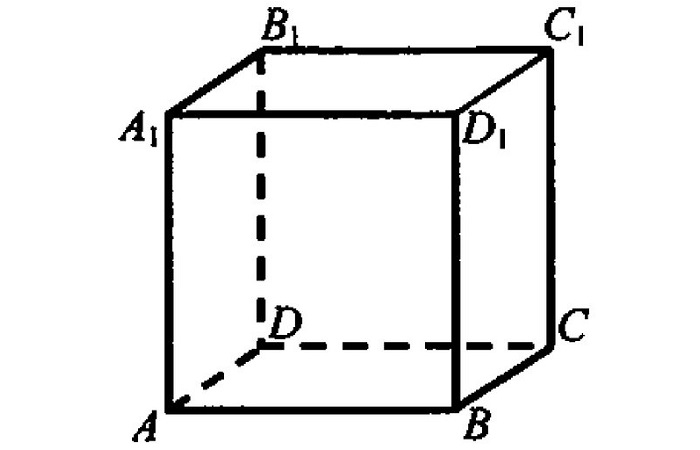
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
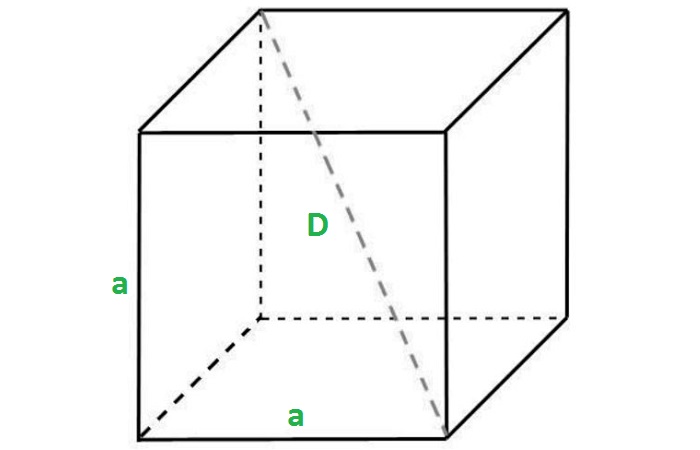
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
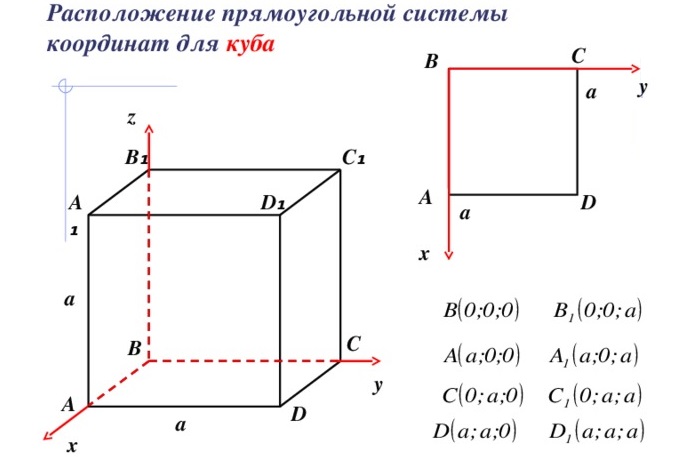
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
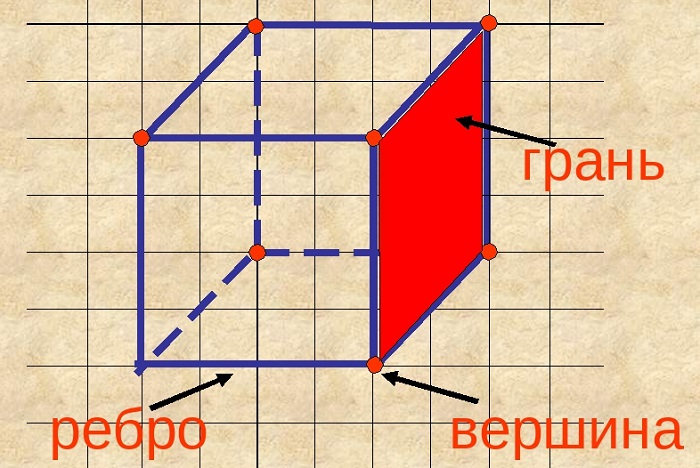
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
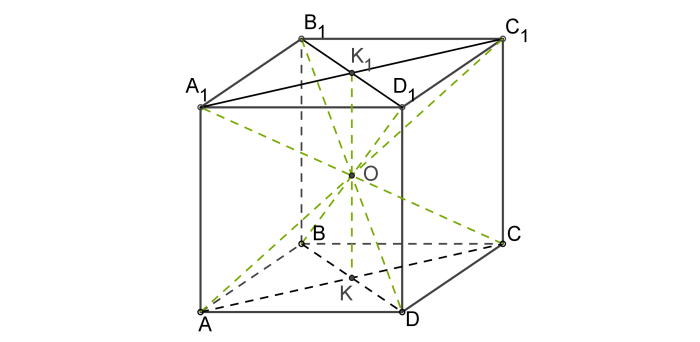
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
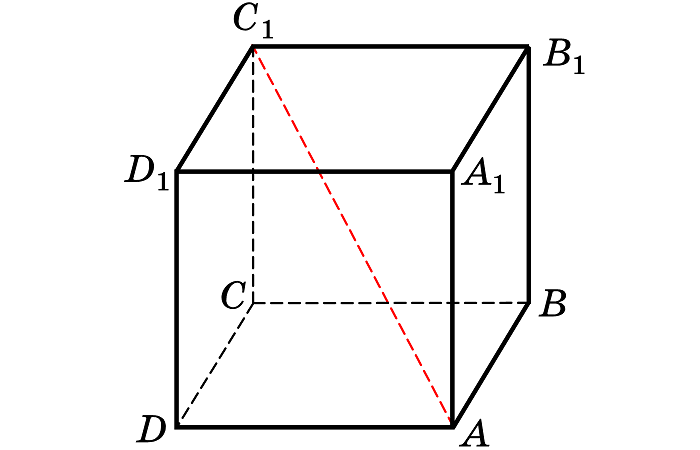
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
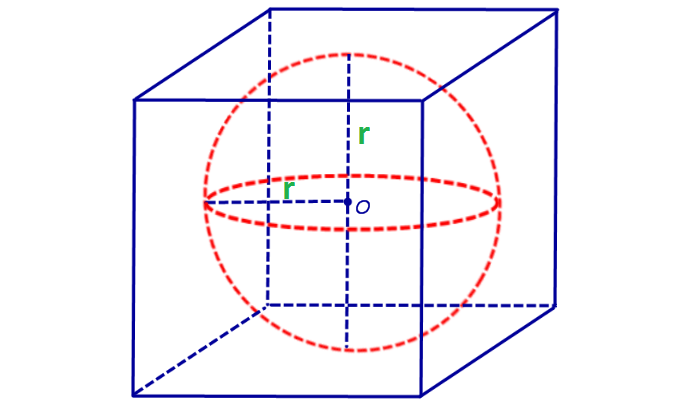
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
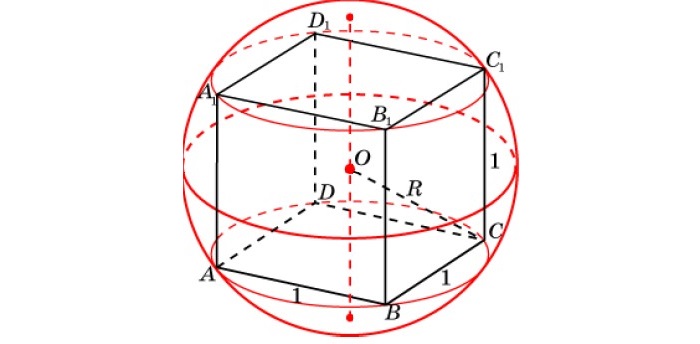
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
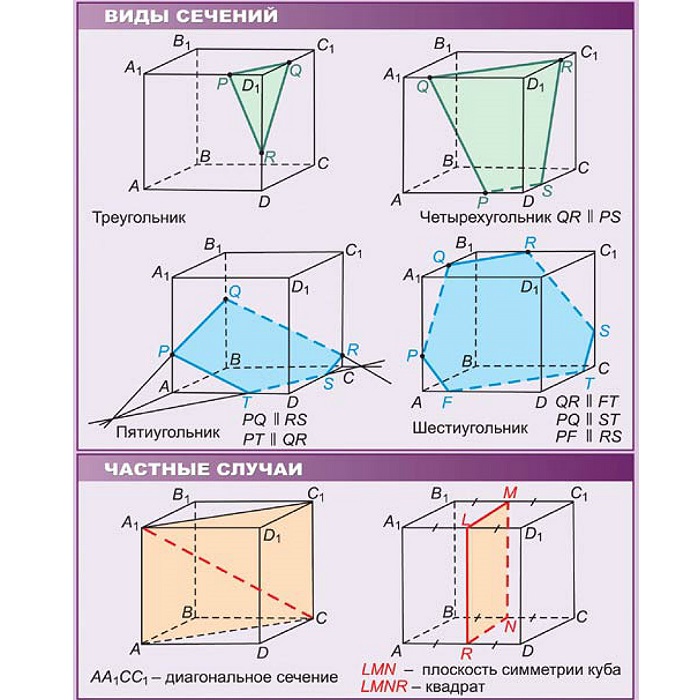
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Площадь поверхности куба.
Площадь поверхности куба – это суммарная площадь всех поверхностей фигуры. Площадь поверхности куба равна сумме площадей всех его шести граней. Площадь поверхности является числовой характеристикой поверхности. Для вычисления площади поверхности куба, Вам необходимо знать определенную формулу и длину одной из сторон куба. Для того чтобы Вы могли оперативно вычислить площадь поверхности куба, вам необходимо запомнить формулу и сам порядок действий. Чуть ниже мы подробно разберем порядок вычисления полной площади поверхности куба и приведем конкретные примеры.
Определение площади поверхности куба.
Чему равна площадь поверхности куба.
Полученное значение возведите в квадрат. Таким образом, Вы возведите в квадрат длину ребра куба. Для того чтобы возвести число в квадрат умножьте его на себя. Наша формула будет иметь следующий вид: SA = 6*а 2
Вы вычислили значение площади одной из граней куба.
a 2 = 2 х 2 = 4 см 2
Полученное значение умножайте на шесть. Не забывайте, что у куба 6 равных граней. Определив площадь одной из граней, умножьте полученное значение на 6, чтобы все грани куба участвовали в расчете.
Вот мы и пришли к конечному действию по вычислению площади поверхности куба.
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.
Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.
Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.
Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.
Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.
Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:
Периметр куба
Сумма длин всех рёбер равна:
Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:
Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.
Радиус равен половине ребра:
Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:
Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.
Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.
Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
у куба все рёбра равны;
один центр и несколько осей симметрии.
Площадь поверхности куба
Онлайн калькулятор

Теория
Площадь поверхности куба через ребро
Чему равна площадь поверхности куба Sпов, если длина его ребра a:
Формула
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если он имеет длину рёбер a = 5 см :
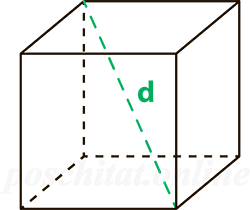
Площадь поверхности куба через диагональ
Чему равна площадь поверхности куба Sпов, если длина диагонали этого куба d:
Формула
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если длина диагонали у него d = 3 м:
Sпов = 2 ⋅ 3² = 2 ⋅ 9 = 18 м² = 180 000 см²
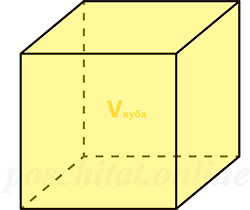
Площадь поверхности куба через объем
Чему равна площадь поверхности куба Sпов, если объём куба Vкуба:
Формула
Пример
Для примера, посчитаем чему равна площадь поверхности куба, если его объём Vкуба = 8 см³:
Sпов = 6 ⋅ 3 √ 8² = 6 ⋅ 3 √ 64 = 6 ⋅ 4 = 24 см²