Что такое правильный четырехугольник
Правильный четырехугольник
Правильный четырехугольник — это такой четырехугольник у которого все четыре стороны равны и его четыре угла равны. Правильный четырехугольник это квадрат.
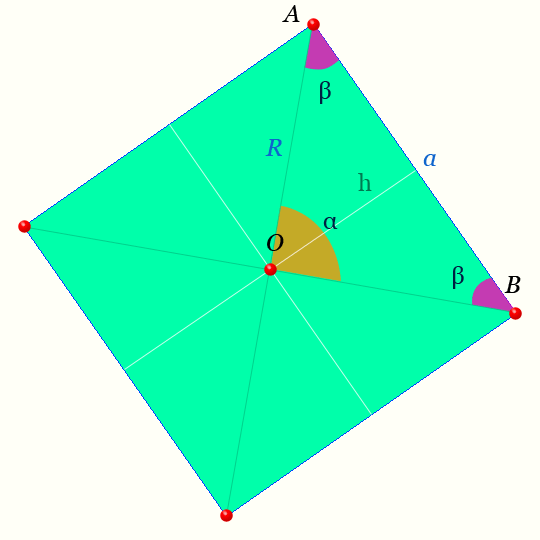
Центр правильного четырехугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Обозначения на рисунке для правильного четырехугольника
| n=4 | число сторон и вершин правильного четырехугольника, | шт |
|---|---|---|
| α | центральный угол правильного четырехугольника, | радианы, ° |
| β | половина внутреннего угла правильного четырехугольника, | радианы, ° |
| γ | внутренний угол правильного четырехугольника, | радианы, ° |
| a | сторона правильного четырехугольника, | м |
| R | радиусы правильного четырехугольника, | м |
| p | полупериметр правильного четырехугольника, | м |
| L | периметр правильного четырехугольника, | м |
| h | апофемы правильного четырехугольника, | м |
Основные формулы для правильного четырехугольника
Периметр правильного четырехугольника
Полупериметр правильного четырехугольника
Центральный угол правильного четырехугольника в радианах
Центральный угол правильного четырехугольника в градусах
Половина внутреннего угла правильного четырехугольника в радианах
Половина внутреннего угла правильного четырехугольника в градусах
Внутренний угол правильного четырехугольника в радианах
Внутренний угол правильного четырехугольника в градусах
Площадь правильного четырехугольника
Или учитывая формулу Площади квадрата получим
Правильный четырехугольник
Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения).
Свойства
См. также
| Правильные многоугольники |
|---|
| Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник |
| (См. также: Многоугольник, Теорема Гаусса — Ванцеля) |
Полезное
Смотреть что такое «Правильный четырехугольник» в других словарях:
ПОНЯТИЕ — общее имя с относительно ясным содержанием и сравнительно четко очерченным объемом. П. являются, напр., «химический элемент», «закон», «сила тяготения», «астрономия», «поэзия» и т.п. Отчетливой границы между теми именами, которые можно назвать П … Философская энциклопедия
Боппард — (Boppard) городок на левом берегу Рейна, в прусском округе Кобленце, в 13 км от города Ст. Гоар, имеет 5526 жителей, занимающихся горшечным промыслом, винокурением, а также виноградарством и торговлей дровами и углем. Во времена римлян на этом… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Конотоп — у. гор. Черниговской губ., в юго вост. углу губернии, на pp. Конотопе и Езусе. Городской земли в гор. черте 751/2 дес. Жит. 23083 (11632 мжч. и 11451 жнщ.). 2037 деревян. и 55 камен. зданий (кроме церквей). Средний доход за 1870 74 гг. 6202 руб … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Спалато — (хорватск. Spljet или Split, итал. Spalato, в памятниках также Spalatro) самый важный порт Далмации, расположен на полуострове Адриатического моря, омывается с северной стороны Canale Castelli, с южной Canale di Spalato, y подножия горы Monte… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Убор головной* — термин, включающий как способы собственно прически, так и способы убранства и покрытия головы. И те, и другие в высшей степени разнообразны в зависимости от расы, места, эпохи, религии, степени культуры и умственного развития. Тем не менее как… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Убор головной — термин, включающий как способы собственно прически, так и способы убранства и покрытия головы. И те, и другие в высшей степени разнообразны в зависимости от расы, места, эпохи, религии, степени культуры и умственного развития. Тем не менее как… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Введенская улица — Введенская улица находится на Петроградской стороне. Она соединяет Кронверкский и Большой проспекты. Первоначально, в 1730 е годы, она именовалась 2 й Большой Белозерской, поскольку находилась в слободе Белозерского полка. Второй… … Санкт-Петербург (энциклопедия)
Стрельна — исторический памятник, поселок на южном берегу Финского залива, расположен в 19 км к западу от Петербурга (см. Санкт Петербург). Административно Стрельна подчинена Петродворцу (см. Петродворец). Мыза Стрельна вблизи речки Стрелки, впадающей в… … Географическая энциклопедия
Медининкайский замок — Медининкайский замок … Википедия
Правильный четырёхугольник
Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения).
Свойства
См. также
| Правильные многоугольники |
|---|
| Треугольник | Четырёхугольник | Пятиугольник | Шестиугольник | Семиугольник | Восьмиугольник | Девятиугольник | Семнадцатиугольник | 257-угольник | 65537-угольник |
| (См. также: Многоугольник, Теорема Гаусса — Ванцеля) |
Полезное
Смотреть что такое «Правильный четырёхугольник» в других словарях:
Правильный четырехугольник — Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения). Квадрат Квадрат правильный четырёхугольник. Свойства Квадрат может быть определён как прямоугольник, у которого две смежные стороны равны ромб, у… … Википедия
Правильный семиугольник — Правильный семиугольник это правильный многоугольник с семью сторонами. Содержание … Википедия
Правильный 17-угольник — Правильный семнадцатиугольник геометрическая фигура, принадлежащая к группе правильных многоугольников. Он имеет семнадцать сторон и семнадцать углов, все его углы и стороны равны между собой, все вершины лежат на одной окружности. Содержание 1… … Википедия
Правильный 65537-угольник — 65537 угольник или окружность? Правильный 65537 угольник (шестѝдесятипятиты̀сячпятисо̀ттридцатисемиугольник) геометрическая фигура из группы правильных многоугольников, состоящая из 65537 … Википедия
Правильный 257-угольник — 257 угольник или окружность? Правильный 257 угольник правильный многоугольник с 257 сторонами. Содержание … Википедия
правильный — I пра/вильный ая, ое; лен, льна, льно. см. тж. правильность 1) а) Соответствующий установленным правилам, не отступающий от существующих правил, норм, порядка. П ое произношение, написание. П ое физическое развитие ребёнка. П ое распределение… … Словарь многих выражений
правильный — I. ПРАВИЛЬНЫЙ ая, ое; лен, льна, льно. 1. Соответствующий установленным правилам, не отступающий от существующих правил, норм, порядка. П ое произношение, написание. П ое физическое развитие ребёнка. П ое распределение энергоресурсов. Он человек… … Энциклопедический словарь
Квадрат (геометрия) — Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения). Квадрат Квадрат правильный четырёхугольник. Свойства Квадрат может быть определён как прямоугольник, у которого две смежные стороны равны ромб, у… … Википедия
Квадрат — Это статья о геометрической фигуре. Другие значения слова см. на странице Квадрат (значения) Квадрат … Википедия
Четырехугольник
Определение четырехугольника
Определение 1. Четырехугольник − это замкнутая ломаная линия, состоящая из четырех звеньев.
Определение 2. Четырехугольник − геометрическая фигура (многоугольник), состоящая из четырех точек, никакие три из которых не лежат на одной прямой и последовательно соединенные четырьмя отрезками, называемыми сторонами четырехугольника.
Объединение четырехугольника и ограниченной им части плоскости также называют четырехугольником.
Любой четырехугольник разделяет плоскость на две части, одна из которых называется внутренней областью четырехугольника, а другая внешней областью четырехугольника.
Виды четырехугольников
Четырехугольники бывают следующих видов:
        |
Обозначение четырехугольника
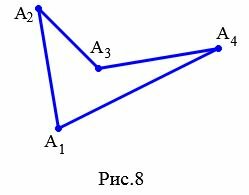
Обозначают четырехугольник буквами, стоящих при его вершинах. Называют четырехугольник чередовав буквы при его вершинах по часовой стрелке или против часовой стрелки. Например, четырехугольник на рисунке 8 называют \( \small A_1A_2A_3A_4 \) или \( \small A_4A_3A_2A_1 \) (Рис.8).
 |
Соседние вершины четырехугольника
Вершины четырехугольника называются соседними, если они являются концами одной из его сторон.
На рисунке 8 вершины \( \small A_2 \) и \( \small A_3 \) являются соседними, так как они являются концами стороны \( \small A_2A_3. \)
Смежные стороны четырехугольника
Стороны четырехугольника называются смежными, если они имеют общую вершину.
На рисунке 8 стороны \( \small A_2A_3 \) и \( \small A_3A_4 \) являются смежными, так как они имеют общую вершину \( \small A_3. \)
Простой четырехугольник. Самопересекающийся четырехугольник
Четырехугольник называется простым, если его несмежные стороны не имеют общих точек (внутренних или концевых).
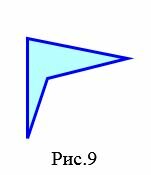  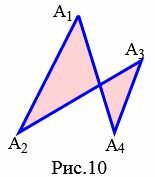 |
На рисунках 9 и 9.1 изображены простые четырехугольники так как стороны четырехугольников не имеют самопересечений. А на рисунке 10 четырехугольник не является простым, так как стороны \( \small A_1A_4 \) и \( \small A_2A_3 \) пересекаются. Такой четырехугольник называется самопересекающийся.
Выпуклый четырехугольник
Четырехугольник называется выпуклым, если она лежит по одну сторону от прямой, проходящей через любую его сторону.
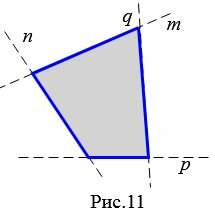 |
На рисунке 11 четырехугольник лежит по одну сторону от прямых \( \small m, \ n, \ p, \ q, \) проходящих через стороны четырехугольника. Поэтому такой четырехугольник выпуклый.
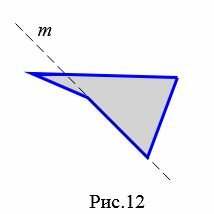 |
На рисунке 12 прямая \( \small m\) делит четырехугольник на две части, т.е. четырехугольник не лежит по одну сторону от прямой \( \small m\). Следовательно, этот четырехугольник не является выпуклым.
Правильный четырехугольник
Простой четырехугольник называется правильным, если все его стороны равны и все углы равны. Квадрат является правильным четырехугольником, так как все его стороны равны и все его углы равны 90°. Среди четырехугольников других правильных четырехугольников не существует.
На рисунке 5 изображен правильный четырехугольник (квадрат), так как у данного четырехугольника все стороны равны и все углы равны. Четырехугольник (ромб) на на рисунке 4 не является правильным, так как все стороны четырехугольника равны, но все его углы не равны друг другу. Прямоугольник также не является правильным четырехугольником, так как несмотря на то, что все углы прямоугольника равны, но все четыре стороны прямоугольника не равны друг другу.
Периметр четырехугольника
Сумма всех сторон четырехугольника называется периметром четырехугольника. Для четырехугольника \( \small A_1A_2A_3A_4 \) периметр вычисляется из формулы:
Угол четырехугольника
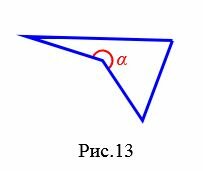
Углом (внутренним углом) четырехугольника при данной вершине называется угол между двумя сторонами четырехугольника, сходящимися к этой вершине. Если четырехугольник выпуклый, то все углы четырехугольника меньше 180°. Если же четырехугольник невыпуклый, то он имеет внутренний угол больше 180° (угол \( \small \alpha \) на рисунке 13).
 |
Внешний угол четырехугольника
Внешним углом четырехугольника при данной вершине называется угол смежный внутреннему углу четырехугольника при данной вершине.
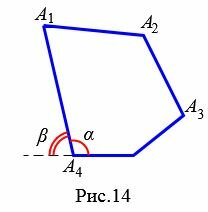 |
На рисунке 14 угол α является внутренним углом четырехугольника при вершине \( \small A_4, \) а углы β и γ являются внешними углами четырехугольника при этой же вершине. Очевидно, что при каждой вершине есть два внешних угла.
Диагональ четырехугольника
Диагоналями называют отрезки, соединяющие две несоседние вершины четырехугольника.
Очевидно, что у четырехугольника две диагонали.
Сумма углов четырехугольника
Для любого простого четырехугольника по крайней мере один диагональ делит его на два треугольника. Сумма углов треугольника равна 180°. Поэтому сумма углов простого четырехугольника равна 360°.
Сумма внешних углов четырехугольника
| \( \small 180°-\angle A_1 \) \( \small +180°-\angle A_2 \) \( \small +180°-\angle A_3 \) \( \small +180°-\angle A_4 \)\( \small =720°-(\angle A_1+\angle A_2+\angle A_3+\angle A_4 )\) \( \small =720°-360°=360°. \) |
Задача 1. Доказать, что длина любой стороны четырехугольника меньше суммы длин трех его сторон.
Правильный четырехугольник (квадрат). Правильний чотирикутник (квадрат)
Квадрат имеет свойства и параллелограмма, и ромба, и прямоугольника.
Квадрат – это прямоугольник, у которого все стороны равны.
У квадрата все стороны равны, как у ромба, и все углы прямые, как у прямоугольника.
Свойства правильного четырехугольника (Квадрата)
1. Все стороны равны и попарно параллельны.
3. Диагонали равны и точкой пересечения делятся пополам.
4. Диагонали взаимно перпендикулярны и являются биссектрисами углов.
5. Точка пересечения диагоналей является общей вершиной четырех треугольников, которые равны между собой.
Квадрат має властивості паралелограма, ромба, прямокутника.
У квадрата всі сторони рівні, як у ромба, і всі кути прямі, як у прямокутника.
Властивості правильного чотирикутника (Квадрата)
1. Всі сторони рівні і попарно паралельні.
2. Все вугілля прямі.
3. Діагоналі рівні і точкою перетину діляться навпіл.
4. Діагоналі взаємно перпендикулярні і є бісектрисами кутів.
5. Точка перетину діагоналей є спільною вершиною чотирьох трикутників, які рівні між собою.
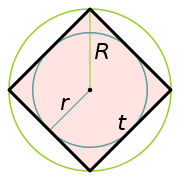
Формулы для квадрата
Радиус вписанной окружности для квадрата равен половине его стороны (Формула 1)
Длина диагонали равна корню квадратному из двух, умноженному на длину стороны (Формула 2)
Радиус описанной окружности равен половине диагонали и равен стороне квадрата, умноженной на корень из двух на два (Формула 3)
Периметр квадрата равен стороне умноженной на четыре или четырем корням из двух, умноженных на радиус описанной окружности или восьми радиусам вписанной окружности (Формула 4)
Радіус вписаного кола для квадрата дорівнює половині його сторони (Формула 1)
Довжина діагоналі дорівнює Корню квадратному з двох, помноженому на довжину сторони (Формула 2)
Радіус описаного кола дорівнює половині діагоналі і дорівнює стороні квадрата, помноженій на корінь з двох на два (Формула 3)
Периметр квадрата дорівнює стороні помноженоi на чотири або чотирьом корням з двох, помножених на радіус описаного кола або восьми радіусам вписаного кола (Формула 4)