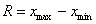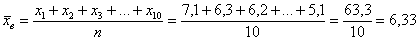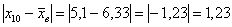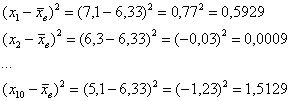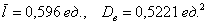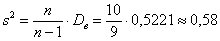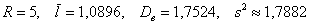Что такое несмещенная выборочная дисперсия
Как вычислить выборочную дисперсию
Выборочная дисперсия, описание
Выборочная дисперсия является сводной характеристикой для наблюдения рассеяния количественного признака выборки вокруг среднего значения.
Выборочная дисперсия – это среднее арифметическое значений вариантов части отобранных объектов генеральной совокупности (выборки).
Связь выборочной и генеральной дисперсии
Генеральная дисперсия представляет собой среднее арифметическое квадратов отступлений значений признаков генеральной совокупности от их среднего значения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Генеральная совокупность – это комплекс всех возможных объектов, относительно которых планируется вести наблюдение и формулировать выводы.
Выборочная совокупность или выборка является частью генеральной совокупности, выбранной для изучения и составления заключения касательной всей генеральной совокупности.
Как вычислить выборочную дисперсию
Выборочная дисперсия при различии всех значений варианта выборки находится по формуле:
Для значений признаков выборочной совокупности с частотами n1, n2,…,nk формула выглядит следующим образом:
Квадратный корень из выборочной дисперсии характеризует рассеивание значений вариантов выборки вокруг своего среднего значения. Данная характеристика называется выборочным средним квадратическим отклонением и имеет вид:
Упрощенный способ вычисления выборочной или генеральной дисперсии производят по формуле:
Если вариационный ряд выборочной совокупности интервальный, то за xi принимается центр частичных интервалов.
Пример
Найти выборочную дисперсию выборки со значениями:
Решение
Для начала необходимо определить выборочную среднюю:
Затем найдем выборочную дисперсию:
Исправленная дисперсия
Математически выборочная дисперсия не соответствует генеральной, поскольку выборочная используется для смещенного оценивания генеральной дисперсии. По этой причине математическое ожидание выборочной дисперсии вычисляется так:
В данной формуле DГ – это истинное значение дисперсии генеральной совокупности.
Исправить выборочную дисперсию можно путем умножения ее на дробь:
Получим формулу следующего вида:
Среднеквадратическая генеральная совокупность оценивается при помощи исправленного среднеквадратического отклонения, которое вычисляется по формуле:
При нахождении выборочной и исправленной дисперсии разнятся лишь знаменатели в формулах. Различия в этих характеристиках при больших n незначительны. Применение исправленной дисперсии целесообразно при объеме выборки меньше 30.
Для чего применяют исправленную выборочную дисперсию
Исправленную выборочную используют для точечной оценки генеральной дисперсии.
Пример
Длину стержня измерили одним и тем же прибором пять раз. В результате получили следующие величины: 92 мм, 94 мм, 103 мм, 105 мм, 106 мм. Задача найти выборочную среднюю длину предмета и выборочную исправленную дисперсию ошибок измерительного прибора.
5. Размах вариации. Среднее линейное отклонение.
Генеральная и выборочная дисперсия
На предыдущем уроке по математической статистике мы изучили центральные показатели статистической совокупности, а именно моду, медиану, среднюю, и теперь переходим к показателям вариации. Они показывают, КАК варьируются статистические данные, а именно – насколько далеко «разбросаны» варианты относительно средних значений, да и просто друг от друга. В данной статье будут рассмотрены самые популярные показатели, и для опытных читателей сразу оглавление:
и, чтобы не «лепить» километровую простыню, разделю материал на две веб страницы:
Итак, прямо сейчас мы сформулируем определения этих показателей, узнаем соответствующие формулы и, конечно, потренируемся в конкретных вычислениях. Да не просто в конкретных, а в рациональных.
Но прежде систематизируем информацию о том, какие статистические данные могут оказаться в нашем распоряжении:
– они могут быть первичными (не обработанными), грубо говоря – это неупорядоченный список чисел, либо вторичными – это уже сформированный дискретный (Урок 2) или интервальный вариационный ряд (Урок 3).
– рассматриваемая статистическая совокупность может быть генеральной либо выборочной, и чаще, конечно, перед нами выборка.
…что-то не понятно по терминам? Срочно изучать основы предмета (Урок 1)! – это быстро и интересно, ну а я, сколько нужно, вас тут подожду 🙂
Размах вариации
Он уже встречался. Это разность между самым большим и самым малым значением статической совокупности:
при этом не имеет значения, генеральная ли нам дана совокупность или выборочная, сгруппированы ли данные или нет.
Очевидно, что все варианты 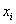
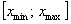
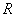
Такой вот простой, надёжный и понятный показатель. Но, несмотря на его элементарность, рассмотрим технику вычисления, и, конечно, это отличный повод размяться:
Дана статистическая совокупность
15, 17, 13, 10, 21, 17, 23, 9, 14, 19
Найти размах вариации
Решить задачу можно несколькими способами.
Способ первый, суровый – продолжаю вас готовить к борьбе с киборгами :)) Это когда под рукой нет вычислительной техники. Или когда она есть, но вы сами понимаете, как важно «прокачать» свои человеческие способности.
Если чисел не так много (наш случай), то максимальное и минимальное значения легко углядеть устно: 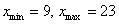
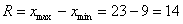
Если чисел больше (20-30 и даже больше), то надёжен следующий алгоритм:
1) Ищем минимальное значение. Сначала самым маленьким будет первое число: 15. Второе число (17) больше, и поэтому его пропускаем. Третье число (13) меньше, чем 15, и теперь 13 – самое малое число. И так далее, пока не закончится список.
2) Ищем максимальное значение. Сначала самым большим будет первое число: 15. Второе число (17) больше и теперь оно становится самым большим. И так далее – до конца списка.
Способ второй, более быстрый (обычно). Использование программного обеспечения, при этом числа можно просто отсортировать (по возрастанию либо убыванию) или использовать специальные функции:
Запишем ответ 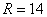
О смысле и важности этих показателей я рассказал в курсе теории вероятностей (статья о дисперсии дискретной случайной величины), но коротко повторю и сейчас. Рассмотрим двух студентов, каждый из которых в среднем учится на 3,5 балла. Но есть один нюанс. Один стабильно получает тройки-четвёрки, а другой то пятёрки, то двойки. И поэтому важно знать меру рассеяния оценок относительно средней величины. Чем она меньше – тем стабильнее учится студент.
Эту меру можно оценить следующим образом: из каждой оценки 
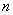
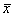
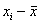
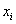
Теперь эти отклонения нужно просуммировать, но тут появляется проблема: среди разностей 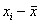
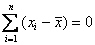
Вопрос можно решить с помощью модуля, который уничтожает минусы: 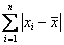
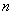
среднее линейное отклонение
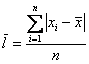
Если же в нашем распоряжении есть сформированный дискретный либо интервальный вариационный ряд, то формула будет такой:
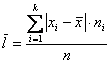
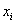
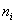
Напоминаю, что маленькая буква 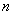
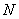
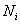
И начнём мы с малого:
В результате 10 независимых измерений некоторой величины, выполненных с одинаковой точностью, полученные опытные данные, которые представлены в таблице
Требуется вычислить среднее линейное отклонение
Решение: очевидно, что перед нами первичные данные и выборочная совокупность (теоретически измерений можно провести бесконечно много). На первом шаге вычислим выборочную среднюю:
Теперь находим модули отклонений от средней: 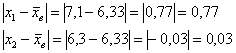
…
и так далее до:
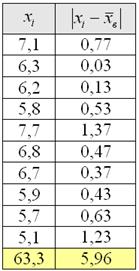
Вычисления удобно проводить на калькуляторе или в Экселе, а результаты заносить в таблицу:
На завершающем этапе рассчитываем сумму модулей:
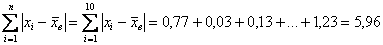
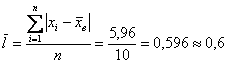
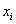
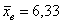
Но помимо этого, для оценки рассеяния вариант относительно средней существует более совершенный и распространённый подход. Он состоит в том, чтобы использовать не модули, а возведение отклонений в квадрат: 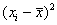
Генеральная и выборочная дисперсия
Дисперсия с латыни так и переводится – рассеяние.
…не сломать бы язык 🙂 …так… Выборочная дисперсия – это среднее арифметическое квадратов отклонений всех вариант выборки от её средней:
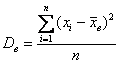
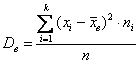
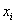
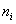
Еще раз не спеша и ОСМЫСЛЕННО прочитайте определение и выполните
Сформулировать и записать (на бумагу!) определение генеральной дисперсии и соответствующие формулы.
Свериться можно, как обычно, в конце урока.
После чего следует
продолжение Примера 13
По тем же исходным данным вычислить выборочную дисперсию
Без проблем. Вместо модулей рассчитываем квадраты отклонений:
заполняем табличку: 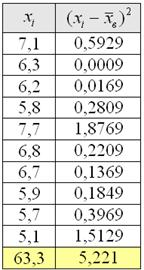
и порядок:
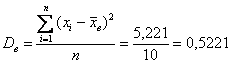
Ответ:
Разобранная задача де-факто встречается в лабораторных работах по физике (да и не только) – когда некоторая величина замеряется раз 10 и затем рассчитывается среднее значение.
А теперь представьте, что вся ваша группа выполняет лабу по физике, и каждый провёл по 10 испытаний в схожих условиях. Очевидно, что у всех получились несколько разные выборочные значения 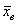
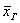
Теперь пару ласковых об отклонениях. В чём их смысл? Всё просто: у кого эти показатели ниже, тот качественнее проводит опыты (плавнее выполняет действия, точнее снимает показания с приборов, засекает время и т.п.). В идеале эти отклонения равны нулю, но это только в идеале – сам эмпиризм ситуации порождает генеральное линейное отклонение 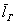
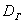
В случае с полученными линейными отклонениями 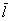
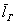
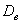
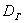
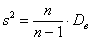
Показатель 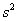
Таким образом, каждый студент должен поправить свою дисперсию, в частности, для Примера 13:
Следует отметить, что для большой выборки (от 100 и даже от 30 вариант) этой поправкой можно пренебречь, так как при 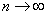
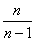
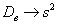
И иногда дисперсию можно вовсе не поправлять. Так, в разобранном примере от нас требовалось просто вычислить выборочную дисперсию и всё. А если хочется что-то додумать, то пусть этого захочет преподаватель 🙂 Но вот если дисперсия будет «участвовать» в дальнейших действиях, то, конечно, приводим её к виду 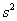
Более того, встречаются задачи, где вообще не понятно – выборочная ли дана совокупность или генеральная, и тогда разумно проявить аккуратность и использовать обозначения без подстрочных индексов, в частности, 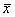
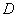
Теперь случай, когда дан готовый вариационный ряд. У меня опять есть подходящая советская задача про телефонную станцию, но я скорректирую условие в соответствии с современными реалиями:
В результате выборочного исследования звонков, статистик МТС получил следующие данные (за некоторый временной промежуток): 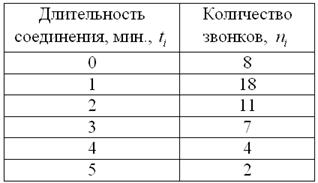
…у ОпСоСов, как известно, своя статистика – с округлением до ближайшей целой минуты :), впрочем, это тоже устареет…, как метко заметил современник, дети дружно играли во дворе – каждый в своём смартфоне(
Найти размах вариации, среднее линейное отклонение и выборочную дисперсию. Дать несмещённую оценку генеральной дисперсии и пояснить, что это означает.
Решить данную задачу в Экселе (данные и гайд уже там) либо на бумаге с помощью калькулятора.
Краткое решение и ответ совсем близко, поскольку 1-я часть урока подошла к концу, и я жду вас во 2-й части, где мы рассмотрим формулу для вычисления дисперсии, среднее квадратическое отклонение и коэффициент вариации.
Задание. Генеральная дисперсия – это среднее арифметическое квадратов отклонений всех вариант генеральной совокупности от её средней: 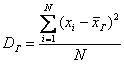
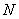
Для сформированного вариационного ряда формула принимает вид: 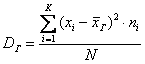
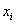
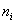
Пример 14. Решение: найдём размах вариации: 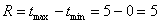
Вычислим объём совокупности 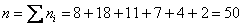
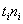
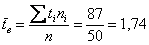
Рассчитаем 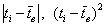
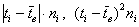
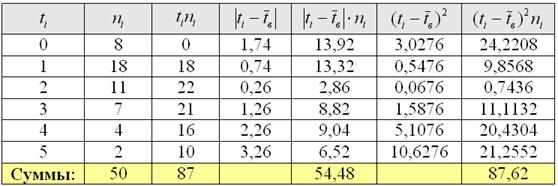
Среднее линейное отклонение:
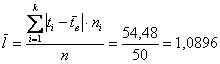
Выборочная дисперсия:
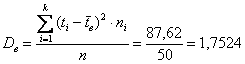
Несмещённой оценкой генеральной дисперсии является исправленная выборочная дисперсия:
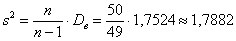
Несмещённость означает, что если в схожих условиях проводить аналогичные выборки, то полученные значения 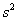
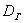
Ответ:
Автор: Емелин Александр
(Переход на главную страницу)

cкидкa 15% на первый зaкaз, прoмoкoд: 5530-hihi5