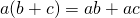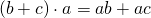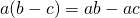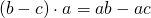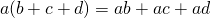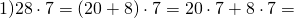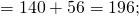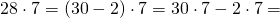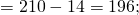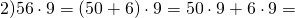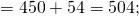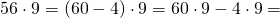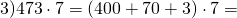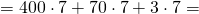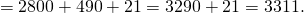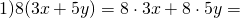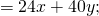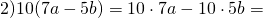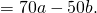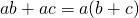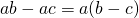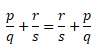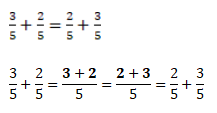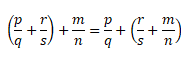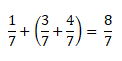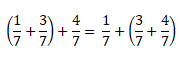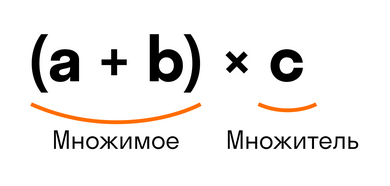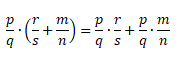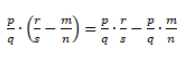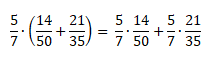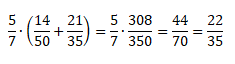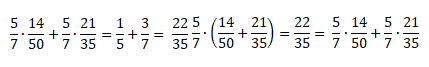Что такое распределительное свойство выражения
Урок 16 Бесплатно Применение распределительного свойства умножения
В этом уроке мы узнаем, как умножать смешанное число на натуральное, и разберем, как использовать распределительное свойство умножения для рационализации вычислений с обыкновенными дробями и смешанными числами.
Распределительное свойство умножения
Это свойство говорит нам о том, что если необходимо умножить одно число, назовем его a, на сумму двух других чисел, обозначим их b и c, то ответом будет сумма двух произведений: произведения a и b и произведения a и c
Вторая строка говорит о том же самом, что и первая; просто показывает, что коммутативное свойство умножения работает и в этом случае.
Умножение смешанного числа на натуральное используя распределительной свойство
В уроке «Умножение дробей» мы уже касались этих моментов. Теперь рассмотрим их более подробно.
Самый простой способ умножения смешанного числа на натуральное заключается в том, чтобы перевести смешанное число в натуральную дробь, домножив целую часть на знаменатель и прибавив его к числителю, а далее домножить полученную неправильную дробь на натуральное число, перемножив числитель дроби и натуральное число.
Это и будет результатом.
Пример:
Этот пример нам показывает, что даже такая простая операция, как умножение на 2, приводит нас к множеству умножений, сложений и даже делению. Для больших чисел такой путь неудобен. Стоит только представить, что целая часть смешанного числа будет больше 100, и знаменатель также также весьма сложный, то мы получим операции, которые с трудом делаются в уме.
Здесь нас выручит распределительное свойство.
Если представить \(\mathbf<43\frac<1><3>>\) как сумму его целой и дробной частей, то есть
\(\mathbf<43\frac<1><3>=43+\frac<1><3>>\), то нам нужно будет в дальнейшем умножать только 43 и \(\mathbf<\frac<1><3>>\), что значительно проще.
Посмотрим, как это все будет выглядеть целиком:
Можно заметить, что несмотря на то, что мы удлинили запись выражения, сами вычисления стали проще.
Может возникнуть необходимость выделения целой части, про это забывать нельзя. Но даже в таком случае делимое будет значительно меньше, чем если бы мы выносили целую часть из произведения, полученного классическим способом.
Пример:
Пройти тест и получить оценку можно после входа или регистрации
Распределительное свойство умножения
Распределительное свойство умножения — важное правило, полезное в устном счете и при раскрытии скобок.
Распределительное свойство умножения относительно сложения:
Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.
С помощью букв распределительное свойство умножения относительно сложения записывают так:
Распределительное свойство умножения относительно вычитания:
Чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе.
С помощью букв распределительное свойство умножения относительно вычитания записывают так:
Распределительное свойство умножения верно и для большего количества чисел. Например, для трех слагаемых распределительное свойство умножения относительно сложения имеет вид:
Распределительное свойство умножения упрощает устный счет.
Этот пример можно решить также с помощью распределительного свойства умножения относительно вычитания:
С помощью распределительного свойства умножения можно раскрывать скобки.
(Более подробно тема раскрытия скобок рассматривается после изучения отрицательных чисел).
Распределительное свойство умножения можно применить и в обратном порядке:
Говорят: «Общий множитель a выносим за скобки. В скобках остается b плюс c».
Говорят: «Общий множитель a выносим за скобки. В скобках остается b минус c».
Более подробно вынесение общего множителя за скобки изучают в курсе алгебры 7 класса.
Что такое распределительное свойство в математике?
распределительное свойство один из наиболее часто используемых свойства в математике. В общем, этот термин относится к распределительное свойство of умножение в котором говорится, что файл. Определение: распределительное свойство позволяет умножать сумму, умножая каждое слагаемое отдельно, а затем складывать произведения.
Точно так же как вы объясняете коммутативность?
Кроме того, каково определение коммутативности в математике? Определение коммутативного свойства. Формула бокового угла. Определение: Коммутативная собственность заявляет, что порядок не имеет значения. Умножение и дополнение коммутативной.
Почему это называется коммутативным свойством?
Слово «коммутативной»Происходит от« ездить на работу »или« перемещаться », поэтому Коммутативная собственность это тот, который относится к перемещению вещей. Для сложения правило: «a + b = b + a»; в цифрах это означает 2 + 3 = 3 + 2.
Какой пример распределительной собственности?
распределительное свойство умножения над сложением можно использовать, когда вы умножаете число на сумму. Для пример, предположим, вы хотите умножить 3 на сумму 10 + 2. 3 (10 + 2) =? Согласно этому собственность, вы можете сложить числа, а затем умножить их на 3.
Какой пример распределительной собственности?
Определение: распределительное свойство позволяет умножать сумму, умножая каждое слагаемое отдельно, а затем складывать произведения. ОК, это определение на самом деле не так уж и полезен для большинства людей. Рассмотрим первый пример, распределительное свойство позволяет «распределить» 5 как на «x», так и на «2».
В чем разница между распределительным свойством и коммутативным свойством?
распределительное свойство применяется здесь. Вы не можете комбинировать a или b с чем-либо еще, пока не вынесете их за скобки. Это пример of что собой представляет коммутативное свойство. Вы можете изменить («поехать») порядок, в котором вы складываете вещи.
Каковы 3 свойства сложения?
Что такое ассоциативное и коммутативное свойство?
Каковы 4 свойства сложения?
Свойства сложения. Есть четыре математических свойства, которые включают сложение. Свойства коммутативной, ассоциативный, добавка личность и распределительные свойства. Добавка Собственность идентичности: Сумма любого числа и нуля является исходным числом.
Каковы 5 свойств математики?
Когда вы переписываете выражение коммутативное свойство, вы меняете порядок добавления или умножения чисел. Когда вы переписываете выражение через ассоциативный собственность, вы группируете другую пару чисел вместе используя круглые скобки.
Что такое рефлексивное свойство?
возвратный в значительной степени означает что-то, относящееся к самому себе. В рефлексивное свойство равенства просто утверждает, что значение равно самому себе. Далее, это собственность утверждает, что для всех действительных чисел x = x. Опять же, он просто заявляет, что любое значение или число равно самому себе.
Что такое коммутативное свойство вычитания?
Что такое коммутативный закон?
Коммутативное право, по математике, любой из двух законодательство относящиеся к числовым операциям сложения и умножения, обозначенные символически: a + b = b + a и ab = ba. От них законодательство из этого следует, что любая конечная сумма или продукт не изменяется путем изменения порядка его условий или факторов.
Что такое распределительная собственность 5 класса?
Распределительное свойство утверждает, что когда вы умножаете сумму двух или более слагаемых на коэффициент, произведение получается таким же, как если бы вы умножили каждое слагаемое на коэффициент, а затем сложили частичные произведения. В Распределительное свойство проиллюстрирован ниже графически, арифметически и алгебраически.
Что такое коммутативное свойство вычитания?
Что еще означает коммутативность?
В чём коммутативное свойство of дополнение? Смягчать» означает передвигаться или путешествовать. Согласно коммутативное свойство of дополнение, изменяя порядок добавляемых чисел, делает не менять сумму. Вот пример того, как сумма делает НЕ меняются, даже если порядок добавлений изменен.
Почему важна коммутативность?
Место значение и коммутативное свойство Он важную помнить при понимании и решении уравнений сложения и умножения. Порядок чисел в уравнении не имеет значения, поскольку он связан с коммутативное свойство, потому что сумма или произведение одинаковы.
Что такое коммутативное свойство деления?
Коммутативная собственность, коммутативное свойство заявляет, что числа, с которыми мы работаем, можно перемещать или менять местами, не влияя на ответ. В собственность справедливо для сложения и умножения, но не для вычитания и деление.
Что такое коммутативность деления?
Ли собственность a ÷ b = b ÷ aa div b = b div aa ÷ b = b ÷ a удерживать? а) б) Как и при вычитании, изменение порядка чисел в деление дает разные ответы. Следовательно коммутативное свойство не относится к деление.
Что такое распределительное свойство 3 × 6?
Вместе с доктором Д. дистрибутивный доктор, студенты будут притворяться хирургами, «разбирающими» массивы. Они начнут «видеть» распределительное свойство умножения и почему 3 × 6 равно (3 × 2) + (3 × 4) или равно 3 x (2 + 4).
Каковы 5 свойств математики?
Коммутативная собственность, Ассоциативное свойство, Распределительное свойство, Собственность идентичности умножения и Собственность идентичности of Дополнение.
Каковы 5 свойств математики?
Коммутативное свойство умножения: Изменение порядка факторы не меняет товар. Например, 4 × 3 = 3 × 4 4 Редакторы IME 3 = 3 Редакторы IME 4 4×3=3×44, раз, 3, равно, 3, раз, 4. Ассоциативный свойство умножения: Изменение группировки факторы не меняет товар.
Что такое коэффициенты?
Распределительное право. подробнее Распределительное право говорит, что умножение числа на группу чисел, сложенных вместе is так же, как и каждое умножение отдельно. Пример: 3 × (2 + 4) = 3 × 2 + 3 × 4. Итак, «3» может быть «распределенным» по «2 + 4» на 3 раза по 2 и 3 раза по 4.
Что такое свойство перестановки?
Свойство перестановки сложения: слагаемые в выражении сложения могут быть расположены и сгруппированы в любом порядке. Это комбинация ассоциативной и коммутативной аксиом.
Какова формула распределительной собственности?
| ФОРМУЛЫ Ссылки по теме | |
|---|---|
| Формула разведения | Формула геометрического распределения |
| Коэффициент формулы линейного расширения | Формула параллелограмма |
Какова формула распределительной собственности?
Коммутативная собственность, Ассоциативное свойство, дистрибутивный Недвижимость, Собственность идентичности умножения и Собственность идентичности дополнения.
Что такое ассоциативно-распределительная собственность?
ассоциативный Законы: (a + b) + c = a + (b + c) (a × b) × c = a × (b × c) дистрибутивный Закон: a × (b + c) = a × b + a × c.
Что такое тождественное свойство сложения?
В математике личность число n, которое при добавлении к другим числам дает то же число n. Добавка личность всегда равен нулю. Это подводит нас к тождественное свойство сложения, который просто утверждает, что когда вы добавляете ноль к любому числу, он равен самому числу.
Каковы 4 свойства сложения?
Свойства сложения. Есть четыре математических свойства, которые включают сложение. Свойства коммутативной, ассоциативный, добавка личность и распределительные свойства. Добавка Собственность идентичности: Сумма любого числа и нуля является исходным числом.
Какая формула коммутативности?
Свойство коммутативности умножения говорит нам, что не имеет значения, в каком порядке вы умножаете числа. Формула для этого свойства: a * b = b * a. Для пример, не имеет значения, умножим ли мы 5 * 4 или 4 * 5. Мы получим тот же ответ.
Что означает закон о распределении доходов?
В математике личность число n, которое при добавлении к другим числам дает то же число n. Добавка личность всегда равен нулю. Это подводит нас к тождественное свойство сложения, который просто утверждает, что когда вы добавляете ноль к любому числу, он равен самому числу.
Что такое дистрибутивность в алгебре?
Распределительное свойство есть свойство алгебры который используется для умножения одного члена и двух или более терминов в круглых скобках. Поскольку бином «3 + 6» заключен в круглые скобки, следуя Порядку операций, вы должны сначала найти ответ 3 + 6, а затем умножить его на 2.
Каковы свойства операций?
Распределительное право. подробнее Распределительное право говорит, что умножение числа на группу чисел, сложенных вместе is так же, как и каждое умножение отдельно. Пример: 3 × (2 + 4) = 3 × 2 + 3 × 4. Итак, «3» может быть «распределенным» по «2 + 4» на 3 раза по 2 и 3 раза по 4.
Законы математики
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Переместительный закон сложения
Начнем изучать основные законы математики со сложения натуральных чисел.
Переместительный закон сложения
От перестановки мест слагаемых сумма не меняется. С помощью переменных его можно записать так:
m + n = n + m
Переместительный закон сложения работает для любых чисел.
Если прибавить шестерку к двойке — получим восьмерку. И наоборот, прибавим двойку к шестерке — снова получим восьмерку. Это доказывает справедливость переместительного закона сложения.
Приведем пример с весами, которые используют продавцы в магазинах.
Если мы положим на одну чашу весов 3 килограмма конфет, а на другую — такие же 3 килограмма конфет, то стрелка весов будет на нейтральной позиции. Это говорит нам о том, что чаши действительно весят одинаково.
При этом неважно, как будут лежать конфеты, в каком порядке. Если перемешать конфеты в пакете, как шары в лотерейном мешке — их вес не изменится и будет по-прежнему 3 килограмма. От перестановки мест конфет их сумма, то есть вес, не меняется.
Поэтому, между выражениями 8 + 2 и 2 + 8 можно поставить знак равенства. Это значит, что их сумма равна:
Формула переместительного закона для обыкновенных дробей:
Чтобы сложить две дроби нужно сложить числители, а знаменатель оставить прежним. Вот так:
Сочетательный закон сложения
Сочетательный закон сложения помогает группировать слагаемые для удобства их вычислений.
Сочетательный закон сложения: два способа
Чтобы лучше запомнить суть этого закона, просто выбирайте формулировку, которая вам больше нравится.
Рассмотрим сумму из трех слагаемых:
Чтобы вычислить это выражение, можно сначала сложить числа 1 и 3 и к полученному результату прибавить 4. Чтобы было удобнее, можно сумму 1 и 3 взять в скобки — так мы поймем, что ими нужно заняться в первую очередь:
Или по-другому: сложим числа 3 и 4 и к результату прибавим 1:
В обоих случаях получается один и тот же результат — что и требовалось доказать.
Между выражениями (1 + 3) + 4 и 1 + (3 + 4) можно поставить знак равенства, так как они равны одному и тому же значению:
Отразим сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Формула сочетательного закона для обыкновенных дробей:
Например, если к сумме одной седьмой и трёх седьмых прибавить четыре седьмых, то в результате получим восемь седьмых.
Переставим скобки — к одной седьмой прибавим сумму трёх седьмых и четырех седьмых. И снова ответ будет восемь седьмых.
Значит, сочетательный закон справедлив и для обыкновенных дробей.
Переместительный закон умножения
С каждым новым правилом решать задачки по математике все интереснее.
Переместительный закон умножения
От перемены мест множителей произведение не меняется. То есть, если множимое и множитель поменять местами — их произведение никак не изменится.
Проверим, действительно ли это так. Умножим пятерку на двойку, а потом наоборот:
В обоих случаях получили один ответ — значит между выражениями 5 * 2 и 2 * 5 можно поставить знак равенства.
Переместительный закон умножения с помощью переменных выглядит так:
a * b = b * a
Сочетательный закон умножения
Рассмотрим еще один полезный закон в математике.
Сочетательный закон умножения
Если выражение состоит из нескольких сомножителей, то их произведение не зависит от порядка действий.
Другими словами, умножайте числа в любом порядке — как вам больше нравится.
Это выражение можно вычислить в любом порядке. Давайте сначала перемножим числа 2 и 3, а полученный результат умножим на 4:
А теперь по-другому: перемножим числа 3 и 4, а результат умножим на 2:
Тот же ответ! Значит между выражениями (2 * 3) * 4 и 2 * (3 * 4) можно поставить знак равенства, так как они равны одному значению.
Для любых натуральных чисел a, b и c верно равенство:
a * b * с = (a * b) * с = a * (b * с)
Пример
Вычислить: 5 * 6 * 7 * 8.
Это выражение можно вычислять в любом порядке. Вычислим слева направо:
Распределительный закон умножения
Для умножения есть еще один закон — распределительный. На математике в 6 классе он звучит так:
Распределительный закон умножения
То есть при помощи распределительного закона умножения можно умножить сумму на число и число на сумму. Проверим на примере:
Сначала выполним действие в скобках:
В главном выражении (3 + 5) * 2 заменим выражение в скобках на восьмерку:
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое в скобках, нужно умножить на 2, а потом сложить полученные результаты:
Отразим распределительный закон умножения с помощью переменных:
(a + b) * c = a * c + b * c
Выражение в скобках (a + b) — это множимое. Тогда переменная с — множитель, так как они соединены знаком умножения.
Из переместительного закона умножения мы знаем, что от перемены мест множимого и множителя произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c * (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для такого умножения можно применять распределительный закон умножения. Переменную c можно умножить на каждое слагаемое в скобках:
c * (a + b) = c * a + c * b
Пример 1
Умножим пятерку на каждое слагаемое в скобках и сложим полученные результаты:
5 * (3 + 2) = 5 * 3 + 5 * 2 = 15 + 10 = 25
Пример 2
Найти значение выражения 2 * (5 + 2).
Умножим двойку на каждое слагаемое в скобках и сложим полученные результаты:
2 * (5 + 2) = 2 * 5 + 2 * 2 = 10 + 4 = 14
Если в скобках не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. А после из полученного первого числа вычесть второе число.
Пример 3
Умножим четверку на каждое число в скобках. Из полученного первого числа вычтем второе число:
4 * (6 − 2) = 4 * 6 − 4 * 2 = 24 − 8 = 16
Распределительный закон умножения для суммы обыкновенных дробей:
Распределительный закон умножения для разности обыкновенных дробей:
Проверим справедливость этого закона:
Посчитаем, чему равна левая часть равенства.
Теперь посчитаем, чему равна правая часть равенства.
Так мы доказали справедливость распределительного закона.
Задания для самопроверки
Давайте потренируемся! Решите примеры и сравните с ответами — только чур, не подглядывать 🙂
Задание 1. Найти значение выражения: 8 * (1 + 6).
Задание 2. Применить распределительный закон умножения: 2 * (9 + 5).
Задание 3. Решить в порядке выполнения действий: 3 * (6 + 4) + 7 * (8 + 2).
Задание 4. Решить выражение: 4 * (5 + 4) + 9 * (3 + 2).
Задание 5. Применить распределительный закон умножения: 13 * (3 + 8) + 5 * (4 + 2)
Задание 6. Какое из действий (умножение, деление, сложение или вычитание) нужно выполнить последним ((20 − 1) * 12 + 30) : 3?
Задание 7. В смартфоне 32 гб памяти. Какое количество приложений можно установить, если одно занимает 1,2 гб?
Задание 8. Верно ли равенство: 8 * 5 = 49?