Что такое рациональные и иррациональные числа примеры

Числа: натуральные, целые, рациональные, иррациональные, действительные

Натуральные числа

Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:

Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.

Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:

с — это всегда натуральное число.

Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:

с — это всегда натуральное число.

Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.

Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b

где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.

Делитель натурального числа — это натуральное число, на которое первое число делится нацело.

Каждое натуральное число делится на единицу и на себя.

Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.

Единицу не считают простым числом.

Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:

Единицу не считают составным числом.

Множество натуральных чисел составляют единица, простые числа и составные числа.

Множество натуральных чисел обозначается латинской буквой N.

Свойства сложения и умножения натуральных чисел:

переместительное свойство сложения

сочетательное свойство сложения

переместительное свойство умножения

сочетательное свойство умножения

распределительное свойство умножения

Целые числа

Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.

Числа, противоположные натуральным — это целые отрицательные числа, например:

Множество целых чисел обозначается латинской буквой Z.

Рациональные числа

Рациональные числа — это целые числа и дроби.

Любое рациональное число может быть представлено в виде периодической дроби. Примеры:

Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.

Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:

Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.

Множество рациональных чисел обозначается латинской буквой Q.

Подробнее о рациональных числах в разделе Рациональные числа.

Иррациональные числа

Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:

Подробнее об иррациональных числах в разделе Иррациональные числа.

Действительные числа

Действительные числа – это все рациональные и все иррациональные числа.

Множество действительных чисел обозначается латинской буквой R.

Источник

math4school.ru

Рациональные и иррациональные числа

Немного теории

Рациональное число – число, представляемое обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число. Любое рациональное число представимо в виде периодической бесконечной десятичной дроби. Множество рациональных чисел обозначается Q.

Если действительное число не является рациональным, то оно иррациональное число. Десятичные дроби, выражающие иррациональные числа бесконечны и не периодичны. Множество иррациональных чисел обычно обозначается заглавной латинской буквой I.

Действительное число называется алгебраическим, если оно является корнем некоторого многочлена (ненулевой степени) с рациональными коэффициентами. Любое неалгебраическое число называется трансцендентным.

Множество рациональных чисел располагается на числовой оси всюду плотно: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел Q и множество натуральных чисел N эквивалентны, то есть между ними можно установить взаимно однозначное соответствие (все элементы множества рациональных чисел можно перенумеровать).

Множество Q рациональных чисел является замкнутым относительно сложения, вычитания, умножения и деления, то есть сумма, разность, произведение и частное двух рациональных чисел также являются рациональными числами.

Все рациональные числа являются алгебраическими (обратное утверждение – неверное).

Каждое вещественное трансцендентное число является иррациональным.

Каждое иррациональное число является либо алгебраическим, либо трансцендентным.

Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число (а значит, и бесконечное множество иррациональных чисел).

Множество иррациональных чисел несчётно.

При решении задач бывает удобно вместе с иррациональным числом a + b √ c (где a, b – рациональные числа, с – целое, не являющееся квадратом натурального числа) рассмотреть «сопряжённое» с ним число a – b √ c : его сумма и произведение с исходным – рациональные числа. Так что a + b √ c и a – b √ c являются корнями квадратного уравнения с целыми коэффициентами.

Задачи с решениями

Итак, предположение ложно, значит, число √ 7 иррациональное.

Итак, предположение ложно, значит, число lg 80 иррациональное.

в) Обозначим данное число через х.

Тогда (х – √ 2 ) 3 = 3, или х 3 + 6х – 3 = √ 2· (3х 2 + 2). После возведения этого уравнения в квадрат получаем, что х должен удовлетворять уравнению

х 6 – 6х 4 – 6х 3 + 12х 2 – 36х + 1 = 0.

Его рациональными корнями могут быть только числа 1 и –1. Проверка же показывает, что 1 и –1 не являются корнями.

Итак, данное число √ 2 + 3 √ 3 является иррациональным.

( √ a – √ b )·( √ a + √ b ) = a – b.

½ ( √ a + √ b ) + ½ ( √ a – √ b ) = √ a

– число рациональное, их разность,

тоже рациональное число, что и требовалось доказать.

3. Докажите, что существуют положительные иррациональные числа a и b, для которых число a b является натуральным.

4. Существуют ли рациональные числа a, b, c, d, удовлетворяющие равенству

где n – натуральное число?

Если выполнено равенство, данное в условии, а числа a, b, c, d – рациональные, то выполнено и равенство:

Но 5 – 4 √ 2 (a – b √ 2 ) 2n + (c – d √ 2 ) 2n > 0. Полученное противоречие доказывает то, что исходное равенство невозможно.

Ответ: не существуют.

Если отрезки с длинами a, b, c образуют треугольник, то неравенство треугольника даёт

Остальные случаи проверки неравенства треугольника рассматриваются аналогично, откуда и следует заключение.

6. Докажите, что бесконечная десятичная дробь 0,1234567891011121314. (после запятой подряд выписаны все натуральные числа по порядку) представляет собой иррациональное число.

8. Доказать, что в каждой бесконечной десятичной дроби существует последовательность десятичных знаков произвольной длины, которая в разложении дроби встречается бесконечно много раз.

9. Докажите элементарным путём, что положительный корень уравнения

Для х > 0 левая часть уравнения возрастает с возрастанием х, и легко заметить, что при х = 1,5 она меньше 10, а при х = 1,6 – больше 10. Поэтому единственный положительный корень уравнения лежит внутри интервала (1,5; 1,6).

Запишем корень как несократимую дробь p/q, где p и q – некоторые взаимно простые натуральные числа. Тогда при х = p/q уравнение примет следующий вид:

откуда следует, что р – делитель 10, следовательно, р равно одному из чисел 1, 2, 5, 10. Однако выписывая дроби с числителями 1, 2, 5, 10, сразу же замечаем, что ни одна из них не попадает внутрь интервала (1,5; 1,6).

Итак, положительный корень исходного уравнения не может быть представлен в виде обыкновенной дроби, а значит является иррациональным числом.

10. а) Существуют ли на плоскости три такие точки A, B и C, что для любой точки X длина хотя бы одного из отрезков XA, XB и XC иррациональна?

б) Координаты вершин треугольника рациональны. Докажите, что координаты центра его описанной окружности также рациональны.

а) Да, существуют. Пусть C – середина отрезка AB. Тогда XC 2 = (2XA 2 + 2XB 2 – AB 2 )/2. Если число AB 2 иррационально, то числа XA, XB и XC не могут одновременно быть рациональными.

б) Пусть (a₁; b₁), (a₂; b₂) и (a₃; b₃) – координаты вершин треугольника. Координаты центра его описанной окружности задаются системой уравнений:

Легко проверить, что эти уравнения линейные, а значит, решение рассматриваемой системы уравнений рационально.

в) Такая сфера существует. Например, сфера с уравнением

(x – √ 2 ) 2 + y 2 + z 2 = 2.

Точка O с координатами (0; 0; 0) – рациональная точка, лежащая на этой сфере. Остальные точки сферы иррациональные. Докажем это.

Допустим противное: пусть (x; y; z) – рациональная точка сферы, отличная от точки O. Понятно, что х отличен от 0, так как при x = 0 имеется единственное решение (0; 0; 0), которое нас сейчас не интересует. Раскроем скобки и выразим √ 2 :

x 2 – 2 √ 2 x + 2 + y 2 + z 2 = 2

√ 2 = (x 2 + y 2 + z 2 )/(2x),

Задачи без решений

1. Докажите, что число

3. Существует ли такое число а, чтобы числа а – √ 3 и 1/а + √ 3 были целыми?

5. Докажите, что при любом натуральном n уравнение (х + у √ 3 ) 2n = 1 + √ 3 не имеет решений в рациональных числах (х; у).

Источник

Базовые сведения об иррациональных числах

Дроби достаточно хороши для любой практической задачи на деление, и некоторое время древние греки были убеждены, что дроби описывают все во Вселенной.
Затем один из них разобрал следствия теоремы Пифагора и задался вопросом о том, как диагональ квадрата относится к его стороне.
Из ответа на этот вопрос следовало, что некоторые задачи решить с помощью дробей невозможно.
Так родились иррациональные числа. Вместе рациональные и иррациональные числа образуют множество действительных чисел.

Прежде чем детально объяснить читателю какие числа являются иррациональными и каковы их свойства, потребуется напомнить некоторые базовые понятия.

Базовые понятия

Натуральными (от латинского “ naturalis ” – “естественный”) называют числа, возникшие из естественной нумерации предметов при счёте – например такие как 1, 2, 3 и так далее. Их последовательность, расположенная в порядке возрастания, образует так называемый натуральный ряд. Существует два конкурентных подхода к определению ряда натуральных чисел: в отечественной математической литературе он традиционно начинается с единицы, в зарубежной – с нуля.

Целыми называют числа, образованные расширением множества натуральных чисел посредством добавления отрицательных чисел и нуля: за счёт такого объединения в общем случае из меньшего числа можно вычесть большее, что уравнивает операции вычитания и сложения, образуя “кольцо целых чисел“.

Рациональными (от латинского “ ratio ” – “дробь”, “отношение”, часто в данном контексте неправильно толкуемое в популярных статьях как определение “разумный” либо аналогичное) числами называют числа вида m/n, где числитель m представлен целым числом, а знаменатель n – натуральным. Иначе говоря, рациональными являются те числа, которые возможно точно представить в виде обыкновенной дроби.

Пояснение-напоминание о дробях

Прежде чем дать определение какие числа называются иррациональными, потребуется напомнить читателю некоторые сведения о дробях и формах их представления. Общепринятыми для записи дробей являются два формата: обыкновенные (вида m/n) и десятичные (вида 0,12345). В случае десятичных дробей дополнительно вводится понятие периодичности: например, дробь 1/7 в десятичном виде может быть представлена как 0,(142857), где в скобках заключён бесконечно повторяющийся фрагмент – так называемый период дроби.

Определение иррациональных чисел

Итак, иррациональные числа – это такие числа, которые невозможно точно отобразить посредством обыкновенной дроби, но возможно представить в виде бесконечной непериодической десятичной дроби. С точки зрения иррациональности в математике, множество иррациональных чисел является разностью между множеством чисел вещественных и множеством чисел рациональных.

С понятием иррационального числа близко столкнулись ещё древние учёные: так, индийский математик Манава обнаружил, что диагональ условного квадрата с единичной стороной имеет размерность √2, что невозможно выразить явно доступными в то время средствами. Другим известным примером является так называемая “постоянная Архимеда” – число Пи (отношение диаметра окружности к её длине). Важно понимать, что для инженерных расчётов возможно использование его рациональных приближений различной степени точности в виде дробей 22⁄7, 179⁄57, 223⁄71 и так далее, но ни одна из этих дробей по определению не является точным представлением числа Пи.

Некоторые примеры рациональных и иррациональных чисел:

рациональные – дроби типа 1/3 или 0,(142857) и им подобные;

иррациональные – квадратные корни √2, √3 и √5, основание натуральных логарифмов e, число Пи и так далее.

Легко заметить, что отрицательные иррациональные числа отличаются от положительных лишь знаком и располагаются на числовой прямой симметрично относительно начала координат (нуля).

Общие признаки рациональных выражений/чисел

Вопрос “как определить иррациональные числа” не имеет однозначного ответа: если имеется некое математическое выражение для числа, то для выяснения его рациональности/иррациональности потребуется произвести детальное исследование. Резко сократить время на поиск требуемого доказательства возможно, если пойти от противного: убрать из рассмотрения числа, не являющиеся иррациональными. По определению, к ним не могут принадлежать:

все целые, натуральные и рациональные числа;

обыкновенные дроби и смешанные числа;

бесконечные и конечные периодические десятичные дроби.

Результат математических операций (сложение, умножение, вычитание и деление) над рациональными числами также не является иррациональным числом. Если в исследуемое выражение входит единственное иррациональное число, то результат также будет иррациональным – однако для случая двух и более вхождений это, вообще говоря, неверно.

Некоторые признаки иррациональных выражений/чисел

Вот некоторые общеупотребительные признаки иррациональности исследуемого выражения/числа:

корень k-ой степени из целого числа будет рациональным только тогда, когда подкоренное выражение является k-ой степенью иного целого числа;

в случае использования обычных логарифмов иррациональность выражения непременно требует доказательства (здесь удобнее всего пользоваться методом “от противного”);

поскольку основанием натуральных логарифмов является иррациональное число e, то натуральный логарифм любого положительного числа также будет иррациональным;

иррациональное число e в любой рациональной (но отличной от нуля!) степени даёт иррациональный результат;

число Пи в любой целой и отличной от нуля степени даёт иррациональный результат;

все основные тригонометрические функции (такие как cos (a), sin (a), tg(a) и ctg (a)) при использовании отличного от нуля рационального аргумента в качестве результата дают иррациональное число.

Интересные факты об иррациональных числах

Как известно Пифагор возвёл числа во главе культа, основным постулатом которого являлось то, что всё во вселенной являлось целочисленном выражении. Его учение собрало последователей в тайное сообщество математиков – пифагорейцев, которое возглавил сам Пифагор. Один из последователей Пифагора – Философ-пифагореец Гиппас высчитал, что в случае, если стороны треугольника равны одной мере длины, то протяженность гипотенузы составит корень из числа 2 ( v2). Ответ полученный при извлечении квадратного корня является целым числом, а значит не имеет точного целочисленного значения, т.е. является ни чем иным как иррациональным числом. Интересный факт в том, что Пифагор, узнав что Гипас ставит под сомнение его учения о целочисленности природы, хоть и не специально, пригласил его на рыбалку, а на берег возвратился уже в одиночку… Гипаса после этой рыбалки никто уже больше не видел.

Выводы

Все вышеперечисленные признаки являются плодом строгого математического доказательства, а иные конкретные частные случаи требуют дополнительного исследования – то есть не существует всеобщих, однозначных и очевидных признаков иррациональности. Например, возведение в иррациональную степень иррационального числа совершенно не обязательно сопровождается получением иррационального результата. Кроме того, имеются частные случаи, когда вычитание, сложение, деление и умножение иррациональных чисел в итоге даёт рациональный результат. В общем случае для доказательства рациональности/иррациональности применяется специальная доказательная база, строящаяся на теории алгебраических и трансцендентных чисел. Особо отметим, что для целого ряда случаев рациональность либо иррациональность выражения/результата не доказана до сих пор.

Источник

Что такое рациональные и иррациональные числа

Содержание статьи

Всё проще, чем кажется!

От абстрактности математических понятий порой настолько веет холодом и отстраненностью, что невольно возникает мысль: «Зачем это всё?». Но, несмотря на первое впечатление, все теоремы, арифметические операции, функции и т.п. – не более, чем желание удовлетворить насущные потребности. Особенно чётко это можно заметить на примере появления различных множеств.

Всё началось с появления натуральных чисел. И, хотя, вряд ли сейчас кто-то сможет ответить, как точно это было, но скорее всего, ноги у царицы наук растут откуда-то из пещеры. Здесь, анализируя количество шкур, камней и соплеменников, человек открыл множество «чисел для счёта». И этого ему было достаточно. До какого-то момента, конечно же.

Казалось бы, уже открытого математического аппарата вполне достаточно, чтобы радоваться жизнью. Но вскоре оказалось, что бывают случаи, когда результат не то, что не целое число, но даже не дробь! И, действительно, квадратный корень из двух никак иначе не выразить с помощью числителя и знаменателя. Или, например, всем известное число Пи, открытое древнегреческим учёным Архимедом, так же не является рациональным. И таких открытий со временем стало настолько много, что все неподдающиеся «рационализации» числа объединили и назвали иррациональными.

Свойства

Рассмотренные ранее множества принадлежат набору фундаментальных понятий математики. Это означает, что их не получится определить через более простые математические объекты. Но это можно сделать с помощью категорий (с греч. «высказывания») или постулатов. В данном случае лучше всего было обозначить свойства данных множеств.

o Иррациональные числа определяют Дедекиндовы сечения в множестве рациональных чисел, у которых в нижнем классе нет наибольшего, а в верхнем нет наименьшего числа.

o Каждое трансцендентное число является иррациональным.

o Каждое иррациональное число является либо алгебраическим, либо трансцендентным.

o Множество иррациональных чисел всюду плотно на числовой прямой: между любыми двумя числами имеется иррациональное число.

o Множество иррациональных чисел несчётно, является множеством второй категории Бэра.

o Это множество упорядоченное, т. е. для каждых двух различных рациональных чисел a иb можно указать, какое из них меньше другого.
o Между каждыми двумя различными рациональными числами существует еще по крайней мере одно рациональное число, а следовательно, и бесконечное множество рациональных чисел.

o Арифметические действия (сложение, вычитание, умножение и деление) над любыми двумя рациональными числами всегда возможны и дают в результате определенное рациональное же число. Исключением является деление на нуль, которое невозможно.

o Каждое рациональное число может быть представлено в виде десятичной дроби (конечной или бесконечной периодической).

Источник

Что такое рациональные и иррациональные числа примеры

Множество иррациональных чисел обычно обозначается заглавной латинской буквой 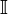в полужирном начертании без заливки. Таким образом: , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа .

Свойства

Примеры

Примеры доказательства иррациональности

Корень из 2

Допустим противное: рационален, то есть представляется в виде несократимой дроби , где — целое число, а — натуральное число. Возведём предполагаемое равенство в квадрат:

.

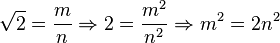
Отсюда следует, что 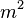чётно, значит, чётно и . Пускай , где целое. Тогда

Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.

Двоичный логарифм числа 3

Допустим противное: рационален, то есть представляется в виде дроби , где и — целые числа. Поскольку 0″ src=»http://upload.wikimedia.org/math/d/1/3/d1351d4222403731e31419faebbe54bc.png» />, и могут быть выбраны положительными. Тогда

Но чётно, а нечётно. Получаем противоречие.

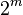
История

Концепция иррациональных чисел была неявным образом воспринята индийскими математиками в VII веке до нашей эры, когда Манава (ок. 750 г. до н. э. — ок. 690 г. до н. э.) выяснил, что квадратные корни некоторых натуральных чисел, таких как 2 и 61, не могут быть явно выражены.

Первое доказательство существования иррациональных чисел обычно приписывается Гиппасу из Метапонта (ок. 500 гг. до н. э.), пифагорейцу, который нашёл это доказательство, изучая длины сторон пентаграммы. Во времена пифагорейцев считалось, что существует единая единица длины, достаточно малая и неделимая, которая целое число раз входит в любой отрезок. Однако Гиппас обосновал, что не существует единой единицы длины, поскольку предположение о её существовании приводит к противоречию. Он показал, что если гипотенуза равнобедренного прямоугольного треугольника содержит целое число единичных отрезков, то это число должно быть одновременно и четным, и нечетным. Доказательство выглядело следующим образом:

Греческие математики назвали это отношение несоизмеримых величин алогос (невыразимым), однако согласно легендам не воздали Гиппасу должного уважения. Существует легенда, что Гиппас совершил открытие, находясь в морском походе, и был выброшен за борт другими пифагорейцами «за создание элемента вселенной, который отрицает доктрину, что все сущности во вселенной могут быть сведены к целым числам и их отношениям». Открытие Гиппаса поставило перед пифагорейской математикой серьёзную проблему, разрушив лежавшее в основе всей теории предположение, что числа и геометрические объекты едины и неразделимы.

Феодор Киренский доказал иррациональность корней натуральных чисел до 17 (исключая, естественно, точные квадраты — 1, 4, 9 и 16), но остановился на этом, так как имевшаяся в его инструментарии алгебра не позволяла доказать иррациональность квадратного корня из 17. По поводу того, каким могло быть это доказательство, историками математики было высказано несколько различных предположений. Согласно наиболее правдоподобному предположению Жана Итара (1961), оно было основано на пифагорейской теории чётных и нечётных чисел, в том числе — на теореме о том, что нечётное квадратное число за вычетом единицы делится на восемь треугольных чисел.

Позже Евдокс Книдский (410 или 408 г. до н. э. — 355 или 347 г. до н. э.) развил теорию пропорций, которая принимала во внимание как рациональные, так и иррациональные отношения. Это послужило основанием для понимания фундаментальной сути иррациональных чисел. Величина стала считаться не числом, но обозначением сущностей, таких как отрезки прямых, углы, площади, объёмы, промежутки времени — сущностей, которые могут меняться непрерывно (в современном понимании этого слова). Величины были противопоставлены числам, которые могут меняться лишь «прыжками» от одного числа к соседнему, например, с 4 на 5. Числа составляются из наименьшей неделимой величины, в то время как величины можно уменьшать бесконечно.

Поскольку никакое количественное значение не сопоставлялось величине, Евдокс смог охватить и соизмеримые, и несоизмеримые величины при определении дроби как отношения двух величин, и пропорции как равенства двух дробей. Убрав из уравнений количественные значения (числа), он избежал ловушки, состоящей в необходимости назвать иррациональную величину числом. Теория Евдокса позволила греческим математикам совершить невероятный прогресс в геометрии, предоставив им необходимое логическое обоснование для работы с несоизмеримыми величинами. «Книга 10 Элементов» Евклида посвящена классификации иррациональных величин.

Средние века

Средние века ознаменовались принятием таких понятий как ноль, отрицательные числа, целые и дробные числа, сперва индийскими, затем китайскими математиками. Позже присоединились арабские математики, которые первыми стали считать отрицательные числа алгебраическими объектами (наряду и на равных правах с положительными числами), что позволило развить дисциплину, ныне называемую алгеброй.

Арабские математики соединили древнегреческие понятия «числа» и «величины» в единую, более общую идею вещественных чисел. Они критически относились к представлениям Евклида об отношениях, в противовес ей они развили теорию отношений произвольных величин и расширили понятие числа до отношений непрерывных величин. В своих комментариях на Книгу 10 Элементов Евклида, персидский математик Аль Махани (ок 800 гг. н. э.) исследовал и классифицировал квадратичные иррациональные числа (числа вида) и более общие кубические иррациональные числа. Он дал определение рациональным и иррациональным величинам, которые он и называл иррациональными числами. Он легко оперировал этими объектами, но рассуждал как об обособленных объектах, например:

Рациональной [величиной] является, например, 10, 12, 3%, 6% и так далее, поскольку эти величины произнесены и выражены количественно. Что не рационально, то иррационально, и невозможно произнести или представить соответствующую величину количественно. Например, квадратные корни чисел таких так 10, 15, 20 — не являющихся квадратами.

В противовес концепции Евклида, что величины суть в первую очередь отрезки прямых, Аль Махани считал целые числа и дроби рациональными величинами, а квадратные и кубические корни — иррациональными. Он также ввел арифметический подход к множеству иррациональных чисел, поскольку именно он показал иррациональность следующих величин:

результат сложения иррациональной величины и рациональной, результат вычитания рациональной величины из иррациональной, результат вычитания иррациональной величины из рациональной.

Египетский математик Абу Камил (ок. 850 г. н. э. — ок. 930 г. н. э.) был первым, кто счел приемлемым признать иррациональные числа решением квадратных уравнений или коэффициентами в уравнениях — в основном, в виде квадратных или кубических корней, а также корней четвёртой степени. В X веке иракский математик Аль Хашими вывел общие доказательства (а не наглядные геометрические демонстрации) иррациональности произведения, частного и результатов иных математических преобразований над иррациональными и рациональными числами. Ал Хазин (900 г. н. э. — 971 г. н. э.) приводит следующее определение рациональной и иррациональной величины:

Пусть единична величина содержится в данной величине один или несколько раз, тогда эта [данная] величина соответствует целому числу… Каждая величина, которая составляет половину, или треть, или четверть единичной величины, или, сравненная с единичной величиной составляет три пятых от нее, это рациональная величина. И в целом, всякая величина, которая относится к единичной как одно число к другому, является рациональной. Если же величина не может быть представлена как несколько или часть (l/n), или несколько частей (m/n) единичной длины, она иррациональная, то есть невыразимая иначе как с помощью корней.

Многие из этих идей были позже переняты европейскими математиками после перевода на латынь арабских текстов в XII веке. Аль Хассар, арабский математик из Магриба, специализировавшийся на исламских законах о наследстве, в XII веке ввел современную символьную математическую нотацию для дробей, разделив числитель и знаменатель горизонтальной чертой. Та же нотация появилась затем в работах Фибоначчи в XIII веке. В течение XIV—XVI вв. Мадхава из Сангамаграмы и представители Керальской школы астрономии и математики исследовали бесконечные ряды, сходящиеся к некоторым иррациональным числам, например, к π, а также показали иррациональность некоторых тригонометрических функций. Джестадева привел эти результаты в книге Йуктибхаза.

Наше время

В XVII веке в математике прочно укрепились комплексные числа, вклад в изучение которых внесли Абрахам де Муавр (1667—1754) и Леонард Эйлер (1707—1783). Когда теория комплексных чисел в XIX веке стала замкнутой и чёткой, стало возможным классифицировать иррациональные числа на алгебраические и трансцендентные (доказав при этом существование трансцендентных чисел), тем самым переосмыслив работы Евклида по классификации иррациональных чисел. По этой теме в 1872 были опубликованы работы Вейерштрасса, Гейне, Кантора и Дедекинда. Хотя ещё в 1869 году Мерэ начал рассмотрения, схожие с Гейне, именно 1872 год принято считать годом рождения теории. Вейерштрасс, Кантор и Гейне обосновывали свои теории при помощи бесконечных рядов, в то время как Дедекинд работал с (ныне так называемым) Дедекиндовым сечением множества вещественных чисел, разделяя все рациональные числа на два множества с определёнными характеристическими свойствами.

Цепные дроби, тесно связанные с иррациональными числами (цепная дробь, представляющая данное число, бесконечна тогда и только тогда, когда число является иррациональным), были впервые исследованы Катальди в 1613 году, затем снова привлекли к себе внимание в работах Эйлера, а в начале XIX века — в работах Лагранжа. Дирихле также внёс значительный вклад в развитие теории цепных дробей.

Источник