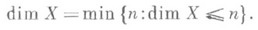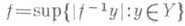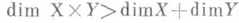Что такое размерность в математике

РАЗМЕРНОСТЬ

Смотреть что такое «РАЗМЕРНОСТЬ» в других словарях:

Размерность — Размерность: В математике Теория размерности часть топологии, в которой изучаются размерности числовые топологические инварианты определённого типа. Размерность пространства количество независимых параметров, необходимых для описания состояния… … Википедия

РАЗМЕРНОСТЬ — число измерений геометрической фигуры. Линия имеет размерность, равную 1 (одномерный образ); поверхность (в частности, плоскость или часть ее) размерность, равную 2 (двумерный образ); пространство, а также любая его ограниченная часть размерность … Большой Энциклопедический словарь

РАЗМЕРНОСТЬ — единицы физической величины, выражение, показывающее, во сколько раз изменится единица данной величины при изменении единиц величин, принятых в данной системе за основные. Р. представляет собой одночлен, составленный из произведения обобщённых… … Физическая энциклопедия

РАЗМЕРНОСТЬ — физической величины, выражение, показывающее связь данной физической величины с величинами, положенными в основу системы единиц. Записывается в виде символов соответствующих основных величин с определенными показателями степеней. Например,… … Современная энциклопедия

РАЗМЕРНОСТЬ — физической величины выражение, показывающее связь данной величины с физическими величинами, положенными в основу системы единиц; записывается в виде произведения символов соответствующих основных величин, возведенных в определенные степени,… … Большой Энциклопедический словарь

РАЗМЕРНОСТЬ — РАЗМЕРНОСТЬ, размерности, мн. нет, жен. (физ.). Выражение, показывающее, из каких основных единиц складывается единица измерения данной величины. Размерность скорости есть отношение длины ко времени. Толковый словарь Ушакова. Д.Н. Ушаков. 1935… … Толковый словарь Ушакова

Размерность — физической величины, выражение, показывающее связь данной физической величины с величинами, положенными в основу системы единиц. Записывается в виде символов соответствующих основных величин с определенными показателями степеней. Например,… … Иллюстрированный энциклопедический словарь

размерность — (вторичной величины в отношении данной первичной величины) Показатель степени при данной первичной величине в формуле размерности … Политехнический терминологический толковый словарь

размерность — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN dimension … Справочник технического переводчика

Источник

РАЗМЕРНОСТЬ

Основы теории Р. были заложены в 1-й пол. 20-х гг. 20 в. в работах П. С. Урысона и К. Менгера. К кон. 30-х гг. была построена теория Р. метризуемых пространств со счетной базой, а к нач. 60-х гг.- теория Р. любых метризуемых пространств.

Ниже все рассматриваемые топологич. пространства считаются нормальными и хаусдорфовыми. В этом случае в определении Р. без ущерба вписываемые открытые покрытия можно заменить на замкнутые.

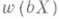
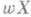
б) существует бикомпактное расширение bХ пространства X, вес к-рого равен весу , и размерность dim bХ равна размерности dim X;аналогичное утверждение верно и для большой индуктивной Р. Особенно интересен случай счетного веса пространства, т. к. в этом случае расширение bХ метризуемо.

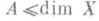
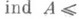
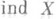
Казалось бы, что Р. должна обладать свойством монотонности: dim , если АМ Х. Это так, если а) множество Азамкнуто в Xили сильно паракомпактно, или б) пространство Xметризуемо (и даже совершенно нормально). Однако уже для подмножества Анаследственно нормального пространства Xможет быть dim A>dim Xи Ind A>Ind Х. Но всегда при АМ Х.

Одним из важнейших вопросов теории Р. является поведение Р. при непрерывных отображениях. В случае замкнутых отображений (к ним принадлежат и все непрерывные отображения бикомпактов) ответ дается формулами В. Гуревича (W. Hurewicz), полученными им первоначально в классе пространств со счетной базой.

Формула Гуревича для повышающих размерность отображений: если отображение 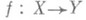непрерывно и замкнуто, то кратность , где кратность

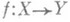
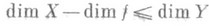
Формула Гуревича для понижающих размерность отображений: для непрерывного замкнутого отображения на па-ракомпакт Yвыполняется неравенство

(1)

где

Для произвольного нормального пространства Yэта формула, вообще говоря, неверна.

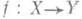
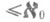
В случае открытых отображений можно показать, что образ нульмерного бикомпакта нульмерен и в то же время гильбертов кирпич есть образ одномерного компакта, даже если соответствующее отображение f имеет размерность dim f, равную нулю. Однако в случае открытого отображения бикомпактов Xи Yкратности выполняется равенство dim X=dim Y.

Поведение Р. при взятии топологич. произведения описывают следующие утверждения:

а) существуют такие конечномерные компакты Xи Y, что ;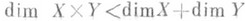

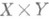
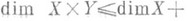
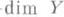
б) если один из сомножителей произведения бикомпактен или метризуем, то ;

в) существуют такие нормальные пространства Xи Y, что

Наиболее содержательна теория Р. прежде всего в классе метрич. пространств со счетной базой и затем в классе любых метрич. пространств. В классе мет-рич. пространств со счетной базой выполняются равенства Урысона

dimX = indX = IndX. (2)

В классе любых метрич. пространств выполняется р а-венство Катетова

и может быть ind X=0 m найдется бикомпакт (метрич. пространство) X с ind X=m,Ind X = n,- неизвестно (1983).

См. также Размерности теория.

Лит.:[1] А л е к с а н д р о в П. С., П а с ы н к о в Б. А., Введение в теорию размерности, М., 1973; [2] Г у р е в и ч В., В о л м э н Г., Теория размерности, пер. с англ., М., 1948; [3] У р ы с о н П. С. Труды по топологии и другим областям математики, т. 1-2, М.- Л., 1951. Б. А. Пасынков.

Источник

Математическая энциклопедия
РАЗМЕРНОСТЬ

Основы теории Р. были заложены в 1-й пол. 20-х гг. 20 в. в работах П. С. Урысона и К. Менгера. К кон. 30-х гг. была построена теория Р. метризуемых пространств со счетной базой, а к нач. 60-х гг.- теория Р. любых метризуемых пространств.

Ниже все рассматриваемые топологич. пространства считаются нормальными и хаусдорфовыми. В этом случае в определении Р. без ущерба вписываемые открытые покрытия можно заменить на замкнутые.

б) существует бикомпактное расширение bХ пространства X, вес к-рого равен весу , и размерность dim bХ равна размерности dim X;аналогичное утверждение верно и для большой индуктивной Р. Особенно интересен случай счетного веса пространства, т. к. в этом случае расширение bХ метризуемо.

Одним из важнейших вопросов теории Р. является поведение Р. при непрерывных отображениях. В случае замкнутых отображений (к ним принадлежат и все непрерывные отображения бикомпактов) ответ дается формулами В. Гуревича (W. Hurewicz), полученными им первоначально в классе пространств со счетной базой.

Формула Гуревича для понижающих размерность отображений: для непрерывного замкнутого отображения на па-ракомпакт Yвыполняется неравенство

Для произвольного нормального пространства Yэта формула, вообще говоря, неверна.

В случае открытых отображений можно показать, что образ нульмерного бикомпакта нульмерен и в то же время гильбертов кирпич есть образ одномерного компакта, даже если соответствующее отображение f имеет размерность dim f, равную нулю. Однако в случае открытого отображения бикомпактов Xи Yкратности выполняется равенство dim X=dim Y.

Поведение Р. при взятии топологич. произведения описывают следующие утверждения:

а) существуют такие конечномерные компакты Xи Y, что ;

б) если один из сомножителей произведения бикомпактен или метризуем, то ;

в) существуют такие нормальные пространства Xи Y, что

Наиболее содержательна теория Р. прежде всего в классе метрич. пространств со счетной базой и затем в классе любых метрич. пространств. В классе мет-рич. пространств со счетной базой выполняются равенства Урысона

dimX = indX = IndX. (2)

В классе любых метрич. пространств выполняется р а-венство Катетова

и может быть ind X=0 m найдется бикомпакт (метрич. пространство) X с ind X=m,Ind X = n,- неизвестно (1983).

См. также Размерности теория.

Лит.:[1] А л е к с а н д р о в П. С., П а с ы н к о в Б. А., Введение в теорию размерности, М., 1973; [2] Г у р е в и ч В., В о л м э н Г., Теория размерности, пер. с англ., М., 1948; [3] У р ы с о н П. С. Труды по топологии и другим областям математики, т. 1-2, М.- Л., 1951. Б. А. Пасынков.

Источник

Презентация по математике «Размерность»

Онлайн-конференция

«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже. Это понятие первично: его нельзя определить, его можно только описать. Нульмерные А В Точки: точка А, точка В

Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Одномерные Линии: прямая, кривая

Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Точка О – центр окружности. Отрезок ОR – радиус окружности

Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Отрезки прямой: отрезок AB, отрезок MD. Лучи: луч с началом в точке О, луч с началом в точке С Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. M D A B O C

Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла. Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом. Угол, равный 90° называется прямым углом. Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°. Углы, градусная мера которых больше 90°, но меньше 180°, называются тупыми углами. Угол В – прямой, угол ВСА – острый, Угол РКТ – тупой.

Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой. Ломаная линия ABCDKE. Точки A,B,C,D,K,E – вершины ломаной. Отрезки AB,BC,CD,DK,KE – звенья ломаной.

Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник. Четырехзвенная замкнутая ломаная линия — четырехугольник Трехзвенная замкнутая ломаная линия — треугольник А В С Е К М О

Треугольник – простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками и тремя отрезками, попарно соединяющими эти точки. Двумерные равносторонний треугольник равнобедренный треугольник А В С T E N

1.Против большей стороны лежит больший угол, и наоборот. 2.Против равных сторон лежат равные углы, и наоборот. В частности, все углы в равностороннем треугольнике равны. 3.Сумма углов треугольника равна 180 º. 4.Продолжая одну из сторон треугольника, можно получить внешний угол. Внешний угол треугольника равен сумме внутренних углов, не смежных с ним. 5.Любая сторона треугольника меньше суммы двух других сторон и больше их разности ( a b – c; b a – c; c a – b ). Основные свойства треугольников:

Прямоугольник – четырёхугольник, у которого все углы прямые (равны 90 градусам). Противоположные стороны прямоугольника попарно равны. Прямоугольник является частным случаем параллелограмма. Четырехугольники

1.Противоположные стороны прямоугольника равны. 2.Диагонали прямоугольника равны. 3.Диагонали прямоугольника пересекаются и точкой пересечения делятся пополам. 4.Диагональ прямоугольника делит его на два равные треугольника. 5.В прямоугольнике сумма углов, прилегающих к одной стороне, равна 180 °. Основные свойства прямоугольника:

Ромб – четырёхугольник, у которого все стороны равны между собой. У ромба есть две диагонали, соединяющие несмежные вершины. Ромб является частным случаем параллелограмма. Ромб с прямыми углами называется квадратом. Свойства: 1.Все свойства параллелограмма. 2.Диагонали ромба взаимно перпендикулярны. 3.Диагонали ромба являются биссектрисами углов. 4.В ромб всегда можно вписать окружность.

Квадрат – правильный четырёхугольник, у которого все стороны и углы равны между собой. У квадрата есть две диагонали, соединяющие несмежные вершины.

1.Все четыре стороны квадрата имеют одинаковую длину, то есть они равны. 2. Противоположные стороны квадрата параллельны. 3. Все четыре угла квадрата прямые. 4. Сумма углов квадрата равна 360 градусов. 5.Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры. 6.Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности. 7.Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные. Основные свойства квадрата:

Трапеция – четырёхугольник, две противоположные стороны которого параллельны между собой, а две другие не параллельны. Параллельные стороны трапеции называются основаниями, а непараллельные — боковыми сторонами. Средняя линия — отрезок, соединяющий середины боковых сторон.

Свойства равнобокой трапеции: 1. Углы при основании равны. 2. Высоты отсекают на большем основании равные отрезки. Равнобокая Разнобокая Прямоугольная Свойства прямоугольной трапеции: 1. Средняя линия равна половине суммы ее оснований. 2. Средняя линия параллельна основаниям трапеции.

Круг – множество точек плоскости, удаленных от заданной точки этой плоскости (центр круга — О) на расстояние, не превышающее заданное (радиус круга).

1.Основания призмы равны 2.Основания призмы лежат в параллельных плоскостях 3.У призмы боковые рёбра параллельны и равны 4.Любая боковая грань является параллелограммом Основные свойства призмы:

Многогранник, составленный из n-угольника А1А2…Аn и n треугольников, называется пирамидой. А1 А2 Аn Р А3

Треугольная пирамида – это тетраэдр Четырехугольная пирамида B А C D S

Пятиугольная пирамида А3 Шестиугольная пирамида А1 А2 Аn Р

Свойства правильной треугольной пирамиды: 1.Боковые ребра правильной пирамиды равны. 2.Все боковые грани правильной пирамиды являются равнобедренными треугольниками. 3.В правильную треугольную пирамиду можно как вписать, так и описать вокруг неё сферу. 4.Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

А1 А2 Аn А3 Усеченная пирамида

Тела вращения Телом вращения называется такое тело, которое плоскостями, перпендикулярными некоторой прямой (оси вращения), пересекается по кругам с центрами на этой прямой.

Объём цилиндра Объём цилиндра равен произведению площади основания на высоту.

Объём конуса Объём конуса равен одной трети произведения площади основания на высоту.

Объём усечённого конуса

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-893673

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Международный конгресс-выставка «Молодые профессионалы» пройдет с 12 по 14 декабря в Москве

Время чтения: 1 минута

ВПР для школьников в 2022 году пройдут весной

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

До конца 2024 года в РФ построят около 1 300 школ

Время чтения: 1 минута

Учителям истории предлагают предоставить право бесплатно посещать музеи

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

РАЗМЕРНОСТЬ

Основы теории Р. были заложены в 1-й пол. 20-х гг. 20 в. в работах П. С. Урысона и К. Менгера. К кон. 30-х гг. была построена теория Р. метризуемых пространств со счетной базой, а к нач. 60-х гг.- теория Р. любых метризуемых пространств.

Ниже все рассматриваемые топологич. пространства считаются нормальными и хаусдорфовыми. В этом случае в определении Р. без ущерба вписываемые открытые покрытия можно заменить на замкнутые.

Одним из важнейших вопросов теории Р. является поведение Р. при непрерывных отображениях. В случае замкнутых отображений (к ним принадлежат и все непрерывные отображения бикомпактов) ответ дается формулами В. Гуревича (W. Hurewicz), полученными им первоначально в классе пространств со счетной базой.

Формула Гуревича для понижающих размерность отображений: для непрерывного замкнутого отображения на па-ракомпакт Yвыполняется неравенство

Для произвольного нормального пространства Yэта формула, вообще говоря, неверна.

В случае открытых отображений можно показать, что образ нульмерного бикомпакта нульмерен и в то же время гильбертов кирпич есть образ одномерного компакта, даже если соответствующее отображение f имеет размерность dim f, равную нулю. Однако в случае открытого отображения бикомпактов Xи Yкратности выполняется равенство dim X=dim Y.

Поведение Р. при взятии топологич. произведения описывают следующие утверждения:

а) существуют такие конечномерные компакты Xи Y, что ;

б) если один из сомножителей произведения бикомпактен или метризуем, то ;

в) существуют такие нормальные пространства Xи Y, что

Наиболее содержательна теория Р. прежде всего в классе метрич. пространств со счетной базой и затем в классе любых метрич. пространств. В классе мет-рич. пространств со счетной базой выполняются равенства Урысона

dimX = indX = IndX. (2)

В классе любых метрич. пространств выполняется р а-венство Катетова

и может быть ind X=0

а) пространство X может быть представлено в виде не более чем n+1 нульмерных слагаемых;

б) существует непрерывное замкнутое отображение кратности нульмерного метрич. пространства на пространство X.

Для любого подмножества Аметрич. пространства Xнайдется такое подмножество типа в X, что dim B=dim A.

Одним из наиболее важных вопросов теории Р. является вопрос о соотношениях между лебеговой и индуктивными Р. Хотя для произвольного пространства Xзначения размерностей dim X,ind X,Ind X, вообще говоря, попарно различны, однако для нек-рых классов пространств, в том или ином смысле близких к метрическим, выполнено, напр., следующее:

а) если пространство Xобладает непрерывным замкнутым отображением f размерности dim f=0 на метрич. пространство, то выполняется равенство (3), отсюда следуют равенства (2) для локально бикомпактных групп и их факторпространств;

б) если существует непрерывное замкнутое отображение метрич. пространства на пространство X, то выполняются равенства (2).

См. также Размерности теория.

Лит.:[1] А л е к с а н д р о в П. С., П а с ы н к о в Б. А., Введение в теорию размерности, М., 1973; [2] Г у р е в и ч В., В о л м э н Г., Теория размерности, пер. с англ., М., 1948; [3] У р ы с о н П. С. Труды по топологии и другим областям математики, т. 1-2, М.- Л., 1951. Б. А. Пасынков.

Источник