Что такое скалярная функция
Скалярная функция
Смотреть что такое «Скалярная функция» в других словарях:
скалярная функция — skaliarinė funkcija statusas T sritis fizika atitikmenys: angl. scalar function vok. skalare Funktion, f rus. скалярная функция, f pranc. fonction scalaire, f … Fizikos terminų žodynas
Функция тока — Функция тока скалярная функция в гидродинамике, которая задаёт двумерное течение жидкости. Содержание 1 Определение 2 Обобщения 3 Неоднозначность … Википедия
функция тока — (Ψ) Скалярная функция, являющаяся следствием уравнения неразрывности и сохраняющая постоянное значение вдоль линий или поверхностей тока. Примечание Функция тока используется для описания плоскопараллельного и осесимметричного течений; ее… … Справочник технического переводчика
Функция тока — скалярная функция (ψ) пространственных координат и времени t, сохраняющая неизменным своё значение на линии тока, то есть удовлетворяющая условию Vgrad(ψ) = 0, где V вектор скорости. В аэро и гидродинамике существование Ф. т. является следствием… … Энциклопедия техники
функция тока — Скалярная функция координат и времени, принимающая в любой момент времени постоянное значение на каждой линии тока и пропорциональная расходу жидкости между поверхностями тока … Политехнический терминологический толковый словарь
Функция Ляпунова — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. В теории обыкновенных дифференциальных уравнений, функция Ляпунова является скалярной функцией, которая… … Википедия
функция тока — функция тока скалярная функция ψ пространственных координат и времени t, сохраняющая неизменным своё значение на линии тока, то есть удовлетворяющая условию Vgradψ = 0, где V вектор скорости. В аэро и гидродинамике существование… … Энциклопедия «Авиация»
функция тока — функция тока скалярная функция ψ пространственных координат и времени t, сохраняющая неизменным своё значение на линии тока, то есть удовлетворяющая условию Vgradψ = 0, где V вектор скорости. В аэро и гидродинамике существование… … Энциклопедия «Авиация»
Скалярная оптимизация — [scalar optimization] совокупность методов решения задач математического программирования, целевая функция которых представляет собой скаляр. Большинство задач, рассматриваемых в словаре (см. Линейное программирование, Нелинейное… … Экономико-математический словарь
скалярная оптимизация — совокупность методов решения задач математического программирования, целевая функция которых представляет собой скаляр. Большинство задач, рассматриваемых в словаре (см. Линейное программирование, Нелинейное программирование, Дискретное… … Справочник технического переводчика
Скалярные функции
Скалярными называют те функции, которые возвращают одно значение. Эти функции могут принимать множество параметров, выполнять вычисления, но в результате выдают одно значение. Эти функции могут использоваться в любых выражениях, даже участвующих в ограничениях проверки. Значение возвращается функцией с помощью оператора return — эта команда должна завершать скалярную функцию.
В скалярных пользовательских функциях не допускаются операции обновления базы данных, но в то же время они могут работать с локальными временными таблицами. Они не могут возвращать данные BLOB (двоичные большие объекты) таких типов, как text, image и ntext, равно как табличные переменные и курсоры.
Скалярные функции создаются, изменяются и удаляются с помощью тех же инструкций DDL, что и другие объекты, хотя синтаксис немного отличается, чтобы определить возвращаемое значение:
CREATE FUNCTION имя_функции (входные_параметры)
RETURNS тип_данных
AS
BEGIN
текст_ функции
RETURN выражение
END
В списке входных параметров должны быть указаны типы данных и, в случае необходимости, значения по умолчанию, аналогично хранимым процедурам (параметр = умолчание). Параметры функции отличаются от параметров хранимых процедур тем, что даже если определены значения по умолчанию, параметры все равно должны присутствовать в вызове функции (т.е. параметры с определенными по умолчанию значениями все равно обязательны). Чтобы запросить значение по умолчанию при вызове функции, ей передается ключевое слово default.
Следующая скалярная функция выполняет простую арифметическую операцию; ее второй параметр имеет значение по умолчанию:
CREATE FUNCTION dbo.Multiply (@A int, @B int = 3)
Скалярные функции могут использоваться в любом месте выражений, где допустимо одно значение. Пользовательские скалярные функции должны всегда вызываться с помощью двухкомпонентного имени (владелец.имя). В следующем примере продемонстрирован вызов ранее созданной функции Multiply:
SELECT dbo.Multiply(7, DEFAULT)
Следующий код создает функцию, возвращающую имя заданного клиента в формате Фамилия И.
CREATE FUNCTION getFICust (@IdCust int)
DECLARE @result varchar(25)
SELECT @result = LName + ‘ ‘ + SUBSTRING(FName, 1, 1) + ‘.’
WHERE IdCust = @IdCust
Тестирование созданной функции:
SELECT dbo.getFICust(IdCust) AS CustName
ORDER BY LName, FName
Задание для самостоятельной работы: Создайте скалярные пользовательские функции, возвращающие:
· Количество товара на складе по заданному уникальному идентификатору товара;
· Суммарную стоимость товаров в заданном заказе.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Скалярная функция
В самом общем случае, числовая функция — это функция, принимающая значения в области вещественных чисел и которая задана на произвольном (чаще всего) метрическом пространстве. Такова, например, индикаторная или характеристическая функция множества. Другой пример числовой функции — это функция расстояния (или, что то же самое, метрика).
Числовые функции, заданные на множестве вещественных или комплексных чисел называются функциями соответственно вещественного или комплексного переменного и являются предметом рассмотрения в анализе:
Важнейший предмет рассмотрения в анализе — представление числовых функций в виде системы приближений (числовых и функциональных рядов).
Числовые функции обладают как общими свойствами, которыми могут обладать отображения произвольных метрических пространств (например, непрерывность), так и рядом свойств, непосредственно связанных с природой числовых пространств. Таковы свойства
Числовые функции широко используются на практике при решении прикладных задач.
Содержание
Свойства
Свойства, связанные с отношением порядка
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Периодичность
Чётность
Экстремумы функции
График функции
Примеры
Способы задания функции
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Аналитический способ
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
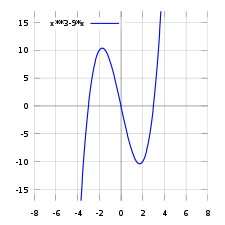
Графический способ
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
Словесный способ
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
Классы числовых функций
Исторический очерк
Появление понятия
Математический термин «функция» впервые появился в 1673 году у Лейбница, и притом не совсем в современном его понимании: Лейбниц вначале называл функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). Позже, однако, в переписке с Иоганном Бернулли (1694) содержание термина расширяется и в конце концов становится синонимом «аналитически заданной зависимости».
В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.
Первые попытки определения
В начале XVIII века были получены разложения всех стандартных функций и многих других. Благодаря, в основном, Эйлеру (1748) были уточнены их определения. Эйлер впервые ясно определил показательную функцию, а также логарифмическую как обратную к ней, и дал их разложения в ряд. До Эйлера многие математики считали, например, тангенс тупого угла положительным; Эйлер дал современные определения всех тригонометрических функций (сам термин «тригонометрическая функция» предложил Клюгель в 1770 году).
В приложениях анализа появляется множество новых трансцендентных функций. Когда Гольдбах и Бернулли попытались найти непрерывный аналог факториала, молодой Эйлер сообщил в письме Гольдбаху о свойствах гамма-функции (1729, название принадлежит Лежандру). Через год Эйлер открыл бета-функцию, и далее неоднократно возвращался к этой теме. Гамма-функция и связанные с ней (бета, дзета, цилиндрические (Бесселя)) находят многочисленные применения в анализе, а также в теории чисел, а дзета-функция Римана оказалась незаменимым инструментом для изучения распределения простых чисел в натуральном ряду.
В 1757 году Винченцо Риккати, исследуя секторы гиперболы, вводит гиперболические функции ch, sh (именно с такими обозначениями) и перечисляет их основные свойства. Немало новых функций возникло в связи с неинтегрируемостью различных выражений. Эйлер определил (1768) интегральный логарифм (название предложил И. Зольднер, 1809), Л. Маскерони — интегральные синус и косинус (1790). Вскоре появляется и новый раздел математики: специальные функции.
С этим пёстрым собранием надо было что-то делать, и математики приняли радикальное решение: все функции, независимо от их происхождения, были объявлены равноправными. Единственное требование, предъявляемое к функции — определённость, причём имеется в виду не однозначность самой функции (она может быть и многозначной), а недвусмысленность способа вычисления её значений.
Первое общее определение функции встречается у Иоганна Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств».
Всё же в XVIII веке отсутствовало достаточно ясное понимание различия между функцией и её аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Бернулли (1753). В основе решения Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»).
Под влиянием теории бесконечных рядов, которые давали алгебраическое представление почти любой гладкой зависимости, наличие явной формулы постепенно перестало быть обязательным для функции. Логарифм или показательная функция, например, вычисляются как пределы бесконечных рядов; такой подход распространился и на другие нестандартные функции. С рядами стали обращаться как с конечными выражениями, первоначально никак не обосновывая корректность операций и даже не гарантируя сходимость ряда.
Начиная с «Дифференциального исчисления» (1755), Эйлер фактически принимает современное определение числовой функции как произвольного соответствия чисел [4] :
Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых.
Общее определение
Близко к современному и определение Лобачевского:
Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле, неоднократно предлагалось и до него. Вот определение Дирихле (1837):
К концу XIX века понятие функции перерастает рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
Примеры
Неявные функции
Функции могут быть заданы при помощи других функций и уравнений.
Скалярная функция
В самом общем случае, числовая функция — это функция, принимающая значения в области вещественных чисел и которая задана на произвольном (чаще всего) метрическом пространстве. Такова, например, индикаторная или характеристическая функция множества. Другой пример числовой функции — это функция расстояния (или, что то же самое, метрика).
Числовые функции, заданные на множестве вещественных или комплексных чисел называются функциями соответственно вещественного или комплексного переменного и являются предметом рассмотрения в анализе:
Важнейший предмет рассмотрения в анализе — представление числовых функций в виде системы приближений (числовых и функциональных рядов).
Числовые функции обладают как общими свойствами, которыми могут обладать отображения произвольных метрических пространств (например, непрерывность), так и рядом свойств, непосредственно связанных с природой числовых пространств. Таковы свойства
Числовые функции широко используются на практике при решении прикладных задач.
Содержание
Свойства [ | ]
Свойства, связанные с отношением порядка [ | ]
(Строго) возрастающая или убывающая функция называется (строго) монотонной.
Периодичность [ | ]
Чётность [ | ]
Экстремумы функции [ | ]
График функции [ | ]
Примеры [ | ]
Способы задания функции [ | ]
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| y | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
Аналитический способ [ | ]
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим. Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью. Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде. Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно. Функция может быть определена разными формулами на разных участках области своего задания. Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Табличный способ [ | ]
Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
Графический способ [ | ]
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостатка точности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции.
Рекурсивный способ [ | ]
Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения.
Словесный способ [ | ]
Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные.
Классы числовых функций [ | ]
Исторический очерк [ | ]
Появление понятия [ | ]
Математический термин «функция» впервые появился в 1673 году у Лейбница, и притом не совсем в современном его понимании: Лейбниц вначале называл функцией различные отрезки, связанные с какой-либо кривой (например, абсциссы её точек). Позже, однако, в переписке с Иоганном Бернулли (1694) содержание термина расширяется и в конце концов становится синонимом «аналитически заданной зависимости».
В первом печатном курсе «Анализа бесконечно малых для познания кривых линий» Лопиталя (1696) термин «функция» не употребляется.
Первые попытки определения [ | ]
В начале XVIII века были получены разложения всех стандартных функций и многих других. Благодаря, в основном, Эйлеру (1748) были уточнены их определения. Эйлер впервые ясно определил показательную функцию, а также логарифмическую как обратную к ней, и дал их разложения в ряд. До Эйлера многие математики считали, например, тангенс тупого угла положительным; Эйлер дал современные определения всех тригонометрических функций (сам термин «тригонометрическая функция» предложил Клюгель в 1770 году).
В приложениях анализа появляется множество новых трансцендентных функций. Когда Гольдбах и Бернулли попытались найти непрерывный аналог факториала, молодой Эйлер сообщил в письме Гольдбаху о свойствах гамма-функции (1729, название принадлежит Лежандру). Через год Эйлер открыл бета-функцию, и далее неоднократно возвращался к этой теме. Гамма-функция и связанные с ней (бета, дзета, цилиндрические (Бесселя)) находят многочисленные применения в анализе, а также в теории чисел, а дзета-функция Римана оказалась незаменимым инструментом для изучения распределения простых чисел в натуральном ряду.
В 1757 году Винченцо Риккати, исследуя секторы гиперболы, вводит гиперболические функции ch, sh (именно с такими обозначениями) и перечисляет их основные свойства. Немало новых функций возникло в связи с неинтегрируемостью различных выражений. Эйлер определил (1768) интегральный логарифм (название предложил И. Зольднер, 1809), Л. Маскерони — интегральные синус и косинус (1790). Вскоре появляется и новый раздел математики: специальные функции.
С этим пёстрым собранием надо было что-то делать, и математики приняли радикальное решение: все функции, независимо от их происхождения, были объявлены равноправными. Единственное требование, предъявляемое к функции — определённость, причём имеется в виду не однозначность самой функции (она может быть и многозначной), а недвусмысленность способа вычисления её значений.
Первое общее определение функции встречается у Иоганна Бернулли (1718): «Функция — это величина, составленная из переменной и постоянной». В основе этого не вполне отчётливого определения лежит идея задания функции аналитической формулой. Та же идея выступает и в определении Эйлера, данном им во «Введении в анализ бесконечных» (1748): «Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого переменного количества и чисел или постоянных количеств».
Всё же в XVIII веке отсутствовало достаточно ясное понимание различия между функцией и её аналитическим выражением. Это нашло отражение в той критике, которой Эйлер подверг решение задачи о колебании струны, предложенное Бернулли (1753). В основе решения Бернулли лежало утверждение о возможности разложить любую функцию в тригонометрический ряд. Возражая против этого, Эйлер указал на то, что подобная разложимость доставляла бы для любой функции аналитическое выражение, в то время как функция может и не иметь его (она может быть задана графиком, «начертанным свободным движением руки»).
Под влиянием теории бесконечных рядов, которые давали алгебраическое представление почти любой гладкой зависимости, наличие явной формулы постепенно перестало быть обязательным для функции. Логарифм или показательная функция, например, вычисляются как пределы бесконечных рядов; такой подход распространился и на другие нестандартные функции. С рядами стали обращаться как с конечными выражениями, первоначально никак не обосновывая корректность операций и даже не гарантируя сходимость ряда.
Начиная с «Дифференциального исчисления» (1755), Эйлер фактически принимает современное определение числовой функции как произвольного соответствия чисел [4] :
Когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых.
Общее определение [ | ]
Близко к современному и определение Лобачевского:
Таким образом, современное определение функции, свободное от упоминаний об аналитическом задании, обычно приписываемое Дирихле, неоднократно предлагалось и до него. Вот определение Дирихле (1837):
К концу XIX века понятие функции перерастает рамки числовых систем. Первыми это сделали векторные функции, вскоре Фреге ввёл логические функции (1879), а после появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
Примеры [ | ]
Неявные функции [ | ]
Функции могут быть заданы при помощи других функций и уравнений.