Что такое скручивающий момент
Деформация кручения. Крутящий момент.
Полярный момент сопротивления кручению. Вращающий (скручивающий) момент.
Кручение возникает при действии на брус двух пар сил (см. рис. 228, г), действующих в плоскостях, перпендикулярных оси бруса. Момент такой пары внешних сил называется
Учитывая, что при кручении происходит сдвиг и что поэтому напряжение в каждой точке пропорционально относительной деформации, и сама относительная деформация зависит от расстояния точки до оси бруса (до центра сечения, называемого полюсом), можно с помощью математических преобразований, приравняв сумму моментов внутренних сил относительно продольной оси бруса внешнему моменту (метод сечения), определить величину максимальных касательных напряжений при кручении (вывод справедлив для бруса круглого сечения диаметром d) следующим образом:
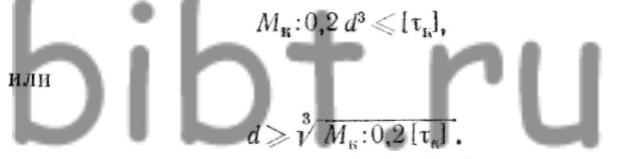
Типовой деталью, испытывающей деформацию кручения, является вал. При проектном расчете на прочность по крутящему моменту и допускаемому напряжению определяют диаметр вала. Исходной является зависимость, в которой в качестве максимальных напряжений используются допускаемые напряжения.
Так как для валов многих машин заранее бывает известен не момент, а передаваемая мощность N и угловая скорость ω вращения вала (или n об/мин), то прежде всего определяют вращающий (скручивающий) момент по формуле M=N:ω, если вместо ω задано n, то ω=πn:30.
Так как М к =М, то далее расчет ведется по вышеприведенной формуле.
При проверочном расчете, как и в случаях других деформаций, определяют действительные напряжения и сравнивают с допускаемыми.
Техническая механика
Сопротивление материалов
Деформация кручения
Основные понятия о кручении. Кручение круглого бруса.
В машинах и механизмах кручению наиболее часто подвергаются круглые или трубчатые валы, поэтому расчеты на прочность и жесткость чаще всего производят для таких узлов и деталей.
Рассмотрим кручение круглого цилиндрического вала.

— ось вала, которую называют осью кручения, останется прямолинейной;
— диаметры окружностей останутся такими же, а расстояние между соседними окружностями не изменится;
— продольные линии на валу обратятся в винтовые линии.
Из этого можно заключить, что при кручении круглого цилиндрического бруса (вала) справедлива гипотеза плоских сечений, а также предположить, что радиусы окружностей остаются при деформации прямыми (поскольку их диаметры не изменились). А поскольку в сечениях вала отсутствуют продольные силы, то расстояние между ними сохраняется.
Следует отметить, что аналогичная картина наблюдается при деформации сдвига, только в этом случае поверхность деформируется из-за поступательного перемещения сечений друг относительно друга, а не из-за вращательного перемещения, как при деформации кручения. На основании этого можно сделать вывод, что при кручении в поперечных сечениях возникают только касательные внутренние силы (напряжения), образующие крутящий момент.
Итак, крутящий момент есть результирующий момент относительно оси бруса внутренних касательных сил, действующих в поперечном сечении.
Материалы раздела «Деформация кручения»:
Большая Энциклопедия Нефти и Газа
Скручивающий момент
Скручивающий момент М к в общем случае нагрузки и формы оси стержня равен сумме моментов внешних сил, действующих по одну сторону от рассматриваемого сечения по отношению к оси, перпендикулярной к плоскости поперечного сечения и проходящей через центр изгиба сечения. [1]
Скручивающий момент от каждого кулачка обычно достигает максимальной величины в конце первого периода подъема толкателя, когда его точка касания с кулачком наиболее удалена от оси толкателя. [2]
Скручивающий момент передается через приклеенные к основаниям цилиндра стальные шайбы. [3]
Скручивающий момент от каждого кулачка обычно достигает максимальной величины в конце первого периода подъема толкателя, когда его точка касания с кулачком наиболее удалена от оси толкателя. [6]
Скручивающие моменты и нагрузки от веса воспринимаются продольными параллельными рычагами, которые принимают на себя также толкающее усилие. [7]
Расчетный скручивающий момент от всех горизонтальных нагрузок Мскр. [9]
Если скручивающий момент достаточно велик, то распространится волна упруго-пластической деформации. [10]
Величина скручивающего момента зависит от положения козелка по длине лыжи. [12]
Наличие скручивающих моментов уменьшает критическое значение продольных сил. Это обстоятельство делает весьма интересным изучение проблемы устойчивости сжато-скрученных стержней. [13]
Добавление скручивающего момента к циклическому растяжению приводит к устойчивому изменению ориентировки фронта трещины. На начальном этапе трещина зарождается по всей длине надреза. Далее наблюдается разворот фронта трещины, и она имеет преимущественно уголковую форму фронта. Активное формирование скосов от пластической деформации сопровождается образованием продуктов контактного взаимодействия черного цвета. Продукты черного цвета являются следствием образования слоя графита за счет пиролиза углеводородных соединений из окружающей среды в зону сильного разогрева металла из-за контактного взаимодействия. Продукты контактного взаимодействия декорируют четко выявляемые усталостные бороздки. В слое графитоподоб-ного вещества находятся продукты контактного взаимодействия. Они представляют собой частицы сферической и эллипсоидной формы. [15]
iSopromat.ru
Кручением называется такой вид деформации бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент T.
Брусья, испытывающие кручение, принято называть валами.
Внутренний крутящий момент
Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.
Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.
Величина крутящего момента в любом сечении вала определяется методом сечений: 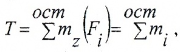
т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.
Правило знаков внутренних скручивающих моментов:
Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.
В технике наиболее широко используются валы круглого поперечного сечения.
Теория кручения круглых валов основана на следующих гипотезах:
Напряжения при кручении
В поперечных сечениях вала при кручении имеют место только касательные напряжения.
Касательные напряжения, направленные перпендикулярно к радиусам, для произвольной точки, отстоящей на расстоянии ρ от центра, вычисляются по формуле: 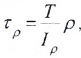
где Iρ — полярный момент инерции.
Эпюра касательных напряжений при кручении имеет следующий вид: 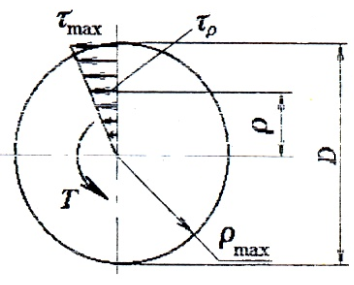
Касательные напряжения меняются по линейному закону и достигают максимального значения на контуре сечения при ρ= ρmax: 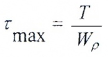
Здесь: 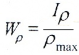
— полярный момент сопротивления.
Геометрические характеристики сечений:
а) для полого вала: 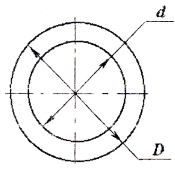
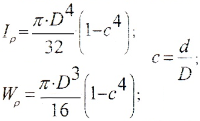
б) для вала сплошного сечения (c=0) 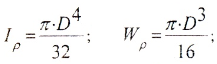
в) для тонкостенной трубы (t 0,9) 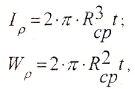
где 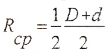
— радиус срединной поверхности трубы.
Деформации
Деформации валов при кручении заключаются в повороте одного сечения относительно другого.
Угол закручивания вала на длине Z определяется по формуле: 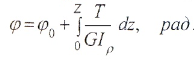
Если крутящий момент и величина GIρ, называемая жесткостью поперечного сечения при кручении, постоянны, для участка вала длиной l имеем: 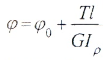
Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания: 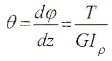
Расчет валов сводится к одновременному выполнению двух условий:
Для стальных валов принимается:
Используя условия прочности и жесткости, как и при растяжении – сжатии можно решать три типа задач:
Из двух найденных значений крутящего момента необходимо принять меньшее.
Потенциальная энергия упругой деформации определяется по формуле 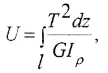
или для участка вала при постоянном T и GIρ
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Тема 2.4. Кручение
Под кручением понимается такой вид деформации, когда в поперечных сечениях бруса действует только крутящий момент Mk, (другое обозначение T, Mz), а остальные силовые факторы (нормальная и поперечная силы и изгибающие моменты) отсутствуют.
Или другое определение кручением называют деформацию, возникающую при действии на стержень пары сил, расположенной в плоскости, перпендикулярной к его оси (рис.1).
Кручение возникает в валах, винтовых пружинах, в элементах пространственных конструкций и т.п.
Деформация кручения наблюдается если прямой брус нагружен внешними моментами (парами сил M), плоскости действия которых перпендикулярны к его продольной оси
В чистом виде деформация кручения встречается редко, обычно присутствуют и другие внутренние силовые факторы (изгибающие моменты, продольные силы).
Стержни круглого или кольцевого сечения, работающие на кручение, называют валами.
Внешние крутящие моменты передаются на вал в местах посадки на него шкивов, зубчатых колес, там, где поперечная нагрузка смещена относительно оси вала.
Мы будем рассматривать прямой брус только в состоянии покоя или равномерного вращения. В этом случае алгебраическая сумма всех внешних скручивающих моментов, приложенных к брусу, будет равна нулю.
При расчете брусьев, испытывающий деформацию кручения, на прочность и жесткость при статическом действии нагрузки, надо решить две основные задачи. Это определение напряжений (от Mk), возникающих в брусе, и нахождение угловых перемещений в зависимости от внешних скручивающих моментов.
При расчете валов обычно бывает известна мощность, передаваемая на вал, а величины внешних скручивающих моментов, подлежат определению. Внешние скручивающие моменты, как правило, передаются на вал в местах посадки на него шкивов, зубчатых колес и т.п.
§2. Построение эпюр крутящих моментов
Для определения напряжений и деформаций вала необходимо знать значения внутренних крутящих моментов Mk (Mz) в поперечных сечениях по длине вала. Диаграмму, показывающую распределение значений крутящих моментов по длине бруса, называют эпюрой крутящих моментов. Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала.
В простейшем случае, когда вал нагружен только двумя внешними моментами (эти моменты из условия равновесия вала ΣMz=0 всегда равны друг другу по величине и направлены в противоположные стороны), как показано на рис. 1, крутящий момент Mz в любом поперечном сечении вала (на участке между внешними моментами) по величине равен внешнему моменту |M1|=|M2|.