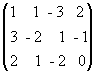Что такое союзная матрица
Обратная матрица
Содержание
Обратимость в алгебре [ править ]
[math]xz=e, \ x[/math] — левый обратный
[math]zy=e, \ y[/math] — правый обратный.
Факт 2. Пусть [math]\exists z^<-1>, \ \tilde
Критерий обратимости матрицы [ править ]
Предположим [math]\exists C: CA=E \Rightarrow \sum\limits_
Свойства обратной матрицы [ править ]
Методы нахождения обратной матрицы [ править ]
Метод Гаусса для нахождения обратной матрицы [ править ]
Пример [ править ]
Найдем обратную матрицу для матрицы
Метод присоединенной матрицы [ править ]
| Определение: |
| Присоединенная(союзная, взаимная) матрица — матрица, составленная из алгебраических дополнений для соответствующих элементов исходной матрицы. |
Алгебраическим дополнением элемента [math]\ a_
[math]M_
Нахождение обратной матрицы
Обратную матрицу можно найти с помощью двух ниже описанных методов.
Нахождение обратной матрицы с помощью присоединённой матрицы
Если к квадратной матрице дописать справа единичную матрицу того же порядка и с помощью элементарных преобразований над строками добиться того, чтобы начальная матрица, стоящая в левой части, стала единичной, то полученная справа будет обратной к исходной.
Решение. Приписываем к заданной матрице 
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
От второй строки отнимаем две первых:
Первую и вторую строки меняем местами:
От второй строки отнимаем две первых:
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.
Если на некотором этапе в «левой» матрице получается нулевая строка, то это означает, что исходная матрица обратной не имеет.
Облегченный способ для матрицы второго порядка
Для матрицы второго порядка можно немного облегчить нахождение обратной, используя следующий алгоритм:
Шаг 2. Элементы, стоящие на главной диагонали меняем местами, а у элементов побочной диагонали меняем знак на противоположный.
Нахождение обратной матрицы не по зубам? Тебе ответит эксперт через 10 минут!
Нахождение обратной матрицы с помощью союзной матрицы
Таким образом, матрица имеет союзную тогда и только тогда, когда она невырожденная.
Решение. Вычисляем определитель матрицы:
Алгоритм вычисления обратной матрицы с помощью алгебраических дополнений: метод присоединённой (союзной) матрицы.
Невырожденная матрица – матрица, определитель которой не равен нулю. Соответственно, вырожденная матрица – та, у которой равен нулю определитель.
Есть несколько способов нахождения обратной матрицы, и мы рассмотрим два из них. На этой странице будет рассмотрен метод присоединённой матрицы, который полагается стандартным в большинстве курсов высшей математики. Второй способ нахождения обратной матрицы (метод элементарных преобразований), который предполагает использование метода Гаусса или метода Гаусса-Жордана, рассмотрен во второй части.
Метод присоединённой (союзной) матрицы
Если решение происходит вручную, то первый способ хорош лишь для матриц сравнительно небольших порядков: второго (пример №2), третьего (пример №3), четвертого (пример №4). Чтобы найти обратную матрицу для матрицы высшего порядка, используются иные методы. Например, метод Гаусса, который рассмотрен во второй части.
Итак, обратная матрица найдена:
$$A^<-1>=\left( \begin
Составляем матрицу из алгебраических дополнений и транспонируем её:
Для матрицы четвёртого порядка нахождение обратной матрицы с помощью алгебраических дополнений несколько затруднительно. Однако такие примеры в контрольных работах встречаются.
Например, для первой строки получим:
А далее продолжаем находить алгебраические дополнения:
Матрица из алгебраических дополнений:
Проверка, при желании, может быть произведена так же, как и в предыдущих примерах.
Во второй части будет рассмотрен иной способ нахождения обратной матрицы, который предполагает использование преобразований метода Гаусса или метода Гаусса-Жордана.
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Нахождение обратной матрицы: три алгоритма и примеры
Что значит найти обратную матрицу?
При решении примеров мы разберём эти действия подробнее. А пока узнаем, что гласит теория об обратной матрице.
Обратной матрицей, которую требуется отыскать для данной квадратной матрицы А, называется такая матрица

произведение на которую матрицы А справа является единичной матрицей, т.е, 
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной, несингулярной), если её определитель не равен нулю, и особенной (или вырожденной, сингулярной), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
На сайте есть онлайн калькулятор для нахождения обратной матрицы. Вы можете открыть его в новом окне уже сейчас, если держите перед собой ваши собственные задания. А мы разберём несколько разминочных.
Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)
Для неособенной квадратной матрицы А обратной является матрица

где 

Пусть существует квадратная матрица A:
Остановимся на минорах и алгебраических дополнениях.
Пусть есть квадратная матрица третьего порядка:

Вычислим алгебраическое дополнение элемента 
Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется следующий определитель, который и является минором элемента 


По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы A’, транспонированной относительно матрицы матрица A.
И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица 

Алгоритм нахождения обратной матрицы методом алгебраических дополнений
1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.
2. Найти матрицу, транспонированную относительно A.
3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.
4. Применить формулу (2): умножить число, обратное определителю матрицы A, на союзную матрицу, найденную на шаге 4.
5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была найдена верно. В противном случае начать процесс решения снова.
Пример 1. Для матрицы
найти обратную матрицу.
Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.
Найдём матрицу, союзную с данной матрицей А.
Найдём матрицу 
Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы, транспонированной относительно матрицы A:
Следовательно, матрица 
Замечание. Порядок вычисления элементов и транспонирования матрицы может быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.
Применяя формулу (2), находим матрицу, обратную матрице А:
Нахождение обратной матрицы методом исключения неизвестных Гаусса



Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась единичная матрица, тогда в правой части на месте единичной матрицы автоматически получится обратная матрица. Матрица A в левой части преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим

Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим

Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её с третьей строкой. Тогда получим

Разделим третью строку на 8, тогда

Умножим третью строку на 2 и сложим её со второй строкой. Получается:

Переставим местами вторую и третью строку, тогда окончательно получим:

Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица 

Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:

В результате должна получиться обратная матрица.
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим

Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим

Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Нахождение обратной матрицы методом линейных преобразований
Матрицы теснейшим образом связаны с системами линейных уравнений. Каждой матрице соответствует система линейных уравнений, коэффициенты в которой есть элементы матрицы. И наоборот, системе линейных уравнений соответствует некоторая матрица.
Алгоритм нахождения обратной матрицы методом линейных преобразований


3. Находим коэффициенты при y: 
4. Пользуясь элементами, найденными на шаге 3, записать найденную обратную матрицу.
Пример 4. Найти обратную матрицу для матрицы

Сначала проверим, не равен ли нулю определитель данной матрицы. Он не равен нулю, следовательно, обратная матрица существует.
Для данной матрицы записываем линейное преобразование:

Находим линейное преобразование, обратное предыдущему, для этого потребуется находить алгебраические дополнения (урок откроется в новом окне). Запишем обратное линейное преобразование:
Найти обратную матрицу самостоятельно, а затем посмотреть решение
Пример 5. Найти обратную матрицу для матрицы

Союзная (присоединенная) матрица
матрица, составленная из алгебраических дополнений для элементов исходной матрицы.
Элементарные преобразования матриц
1. умножение строки или столбца матрицы на ненулевое число;
2. перестановка местами двух строк или столбцов матрицы;
3. прибавление к некоторой строке матрицы другой ее строки, предварительно умноженной на произвольный коэффициент;
4. прибавление к некоторому столбцу матрицы другого ее столбца, предварительно умноженного на произвольный коэффициент.
Ранг матрицы.
1)Умножение строки(столбца на числ, отличное от нуля.
2)Прибавление к одной строке(столбцу) другой, умножение на любое число.
3)Перемена местами двух строк(столбцов)
4)Вычёркивание нулевой строки
Базисные строки и столбцы
Столбцы и строки, на которых расположены элементы базисного минора
14.Система m линейных уравнений с n неизвестными (или, линейная система) в линейной алгебре — это система уравнений вида
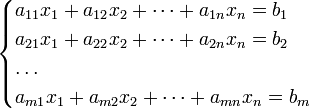 Теорема Кронекера – Капели Теорема Кронекера — Капе́лли —Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. Теорема Кронекера – Капели Теорема Кронекера — Капе́лли —Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных. |
Метод Крамера
При небольшой размерности системы m (m = 2,…,5) на практике часто используют формулы Крамера для решения СЛАУ:

Метод Гаусса
Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Решить систему уравнений методом Гаусса:
Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:

б) третью строку умножим на (-5) и прибавим к ней вторую:

В результате всех этих преобразований данная система приводится к треугольному виду:
16. Метод обратной матрицы решения систем алгебраических уравнений Если det A ≠ 0, то существует обратная матрица