Что такое статическая характеристика прямой передачи по току
Характеристики биполярного транзистора
Статические характеристики биполярного транзистора c ОЭ
Статические характеристики биполярного транзистора отражают зависимость между напряжениями и токами на его входе и выходе при отсутствии нагрузки.
Эти характеристики будут разные в зависимости от выбранного способа включения транзистора. В основном применяются характеристики со схемами включения с общей базой (ОБ) и общим эмиттером (ОЭ).
Входные характеристики биполярного транзистора
Выходные характеристики биполярного транзистора
По выходной характеристике транзистора МП42Б ( рис.6 ) определим в точке Б коллекторный ток при Uкэ = 5,7 В и Iб = 40 μA. Он будет равен Iк = 4,5 mA.
А для точки А ток базы при коллекторном напряжении Uкэ = 5,7 В и Iк = 8 mA будет Iб = 80 μA.
Так же по выходной характеристике этого транзистора можно найти выходные сопротивления для постоянного и переменного токов.
Сопротивление по постоянному току в точке Б будет равно:
Rвых_= Uкэ/Iк = 5,7/4,5•10ˉ³ = 1,3 кОм.
Сопротивление по переменному току при приращении:
∆U = 8-3 = 5 В; ∆I = 4,5-4 = 0,5 mA
равно:
Rвых
= ∆U/∆I = 5/0,5•10ˉ³ = 10 кОм.
Это cопротивление может достигать 50 кОм.
Статические характеристики биполярного транзистора с ОБ.
Входные характеристики биполярного транзистора
.
По параметрам входной характеристики ( рис.9 ) найдем входные сопротивления в точке А :
∆Uэб= 0,225-0,175 = 0,05 В,
∆Iэ = 16- 6 = 10 mA.
Rвх_= Uбэ/Iэ = 0,2/10•10ˉ³ =20 Ом,
Rвх
= ∆Uэб/∆Iэ =0,05/10•10ˉ³ = 5 Ом.
Вывод: входные сопротивления в схеме с ОБ на много меньше чем с ОЭ и обычно не превышают 100 Ом.
Выходные характеристики биполярного транзистора
Статические характеристики прямой передачи по току биполярного транзистора
По характеристике прямой передачи транзистора по току, которая представляет собой связь между входным и выходным токами, можно определить коэффициенты усиления по току в схеме с ОЭ и ОБ как на рис.11
.Коэффициент усиления по току с ОЭ равен:
β=∆Iк/∆Iб
где ∆Iк=2,8-2=0,8 mA;
∆Iб=30-20=10 μА.
β=0,8/10•10ˉ³= 80.
Коэффициент усиления по току с ОБ равен:
α=∆Iк/∆Iэ
где ∆Iк=2,8-2=0,8 mA;
∆Iэ=3-2=1 mA;
α=0,8/1=0,8.
Можно сделать вывод, что при включении транзистора с ОБ усиление по току почти не происходит.
БИПОЛЯРНЫЕ ТРАНЗИСТОРЫ
Биполярнымтранзистором называют полупроводниковый прибор, состоящий из трех областей счередующимися типами электропроводности и предназначеный для усиления сигнала.
Биполярныетранзисторы являются полупроводниковыми приборами универсального назначения ишироко применяются в различных усилителях, генераторах, в импульсных и ключевыхустройствах.
Втаких транзисторах ток определяется движением носителей заряда двух типов:электронов и дырок. Отсюда пошло их название: биполярные.
Средняяобласть транзистора называется базой, одна крайняя область – эмиттером, вторая– коллектором. Таким образом в транзисторе имеются два р- n – перехода: эмиттерный – между эмиттером и базой и коллекторный– между базой и коллектором.
Эмиттером- это область транзистора для инжекции носителейзаряда в базу. Коллектором – область, назначением которой является извлечениеносителей заряда из базы. Базой называется область, в которую инжектируютсяэмиттером неосновные для этой области носители заряда.
Концентрацияосновных носителей заряда в эмиттере во много раз больше концентрации основныхносителей заряда в базе, а в коллекторе несколько меньше концентрации в эмиттере. Поэтомупроводимость эмиттера гораздо выше проводимости базы, а проводимостьколлектора меньше проводимости эмиттера.
В зависимости от того, какой извыводов является общим для входной и выходной цепей, различают три схемывключения транзистора: с общей базой (ОБ), общим эмиттером (ОЭ), общимколлектором (ОК).
Входная,или управляющая, цепь служит для управления работой транзистора. В выходной,или управляемой, цепи получаются усиленные колебания. Источник усиливаемыхколебаний включается во входную цепь, а в выходную включается нагрузка.
Внешниенапряжения двух источников питания ЕЭ и Е к подключают к транзистору таким образом, чтобыобеспечивалось смещение эмиттерного перехода П1 в прямом направлении,а коллекторного перехода П2 – в обратном направлении.
Привключении в цепь эмиттера постоянного напряжения ЕЭ в прямом направлениипотенциальный барьер эмиттерного перехода понижается. Начинается инжектированиедырок в базу.
Такимобразом, в б иполярном транзисторе протекает три вида тока: эмиттера, коллектора и базы.
Впроводе, являющемся выводом базы, токи эмиттера и коллектора направленывстречно. Ток базы равен разности токов эмиттера и коллектора: I Б = I Э − I К.
Выходнойток транзистора зависит от входного тока. Поэтому транзистор- прибор,управляемый током.
Схемы включения биполярных транзисторов
Статические характеристики биполярных транзисторов
Статическимрежимом работы транзистора называется режим при отсутствии нагрузки в выходнойцепи.
Статическимихарактеристиками транзисторов называют графически выраженные зависимостинапряжения и тока входной цепи (входные ВАХ) и выходной цепи (выходные ВАХ).Вид характеристик зависит от способа включения транзистора.
Характеристики транзистора, включенного по схеме ОБ
Входнойхарактеристикой является зависимость:
I Э = f ( U ЭБ) при U КБ= const (а).
Выходнойхарактеристикой является зависимость:
I К = f ( U КБ) при I Э= const (б).
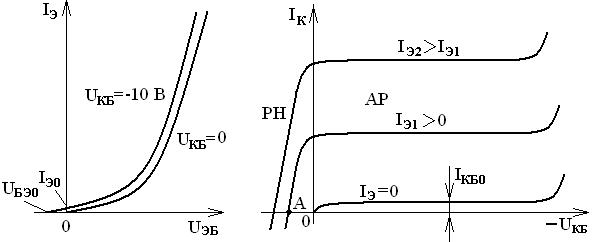
Статические характеристики биполярного транзистора, включенного по схемеОБ. ВыходныеВАХ имеют три характерные области: 1 – сильная зависимость I к от U КБ; 2 – слабая зависимость I к от U КБ; 3 – пробой коллекторного перехода. Особенностьюхарактеристик в области 2 является их небольшой подъем при увеличениинапряжения U КБ.
Характеристики транзистора, включенного по схеме ОЭ:
Входнойхарактеристикой является зависимость:
I Б = f ( U БЭ) при U КЭ= const (б).
Выходнойхарактеристикой является зависимость:
I К = f ( U КЭ) при I Б= const (а).
Режим работы биполярного транзистора
Транзисторможет работать в трех режимах в зависимости от напряжения на его переходах. Приработе в активном режиме на эмиттерном переходе напряжение прямое, а наколлекторном – обратное.
Режим отсечки, или запирания,достигается подачей обратного напряжения на оба перехода (оба р- n – перехода закрыты).
Если же на обоих переходах напряжениепрямое (оба р- n – переходаоткрыты), то транзистор работает в режиме насыщения. В режиме отсечки и режиме насыщенияуправление транзистором почти отсутствует. В активном режиме такое управлениеосуществляется наиболее эффективно, причем транзистор может выполнять функцииактивного элемента электрической схемы – усиление, генерирация.
усилительный каскад на биполярном транзисторе
Резистор R Б, включенный в цепьбазы, обеспечивает работу транзистора при отсутствиивходного сигнала. Режим покоя обеспечивается током базы покоя I Б = Е к / R Б. Спомощью резистора R к создается выходноенапряжение. R к выполняет функциюсоздания изменяющегося напряжения в выходной цепи за счет протекания в нейтока, управляемого по цепи базы.
Дляколлекторной цепи усилительного каскада можно записать следующее уравнение электрическогосостояния:
Процессусиления основывается на преобразовании энергии источника постоянногонапряжения Е к вэнергию переменного напряжения в выходной цепи за счет изменения сопротивленияуправляемого элемента (транзистора) по закону, задаваемого входным сигналом.
Статические характеристики биполярных транзисторов



В качестве статических характеристик БТ используются функциональные зависимости между токами и напряжениями, прикладываемыми к их электродам: входная характеристика I1 = f(U1) при U2 = const; характеристикаобратной связи U1=f(U2) при I1 = const; характеристика прямой передачи I2=f(I1) при U2 = const; выходнаяхарактеристика I2 = f(U2) при I1 = const.
Для определения параметров и расчета функциональных узлов достаточно иметь входные и выходные характеристики БТ в схемах с общей базой и общим эмиттером.
Для определенности и преемственности изложения будем рассматривать
Схема с общей базой
При UКБ = 0 характеристика подобна ВАХ p-n-перехода. С ростом обратного напряжения UКБ (UКБ
| а) | б) |
| Рис. 3.5. Характеристики БТ в схеме включения с ОБ: а) входные характеристики; б) выходные характеристики |
Семейство выходных характеристик схемы с ОБ представляет собой зависимости IК = f(UКБ)при заданных значениях тока эмиттера IЭ (рисунок 3.5, б). Выходная характеристика p-n-p-транзистора при IЭ = 0 и обратном напряжении UКБ 0 основная часть инжектированных в базу носителей (дырок в
p-n-p-транзисторе) доходит до границы коллекторного перехода и создает коллекторный ток при UКБ = 0 в результате ускоряющего действия контактной разности потенциалов. Ток можно уменьшить до нуля путем подачи на коллекторный переход прямого напряжения определенной величины. Этот случай соответствует режиму насыщения, когда существуют встречные потоки инжектированных дырок в базу из эмиттера и коллектора. Результирующий ток станет равен нулю, когда оба тока будут одинаковы по величине (например, точка А на рисунке 3.5, б). Чем больше заданный ток IЭ, тем большее прямое напряжение UКБ требуется для получения IК = 0.
Область в первом квадранте на рисунке 3.5, б, где UКБ 0 (что означает прямое напряжение) соответствует активному режиму (АР). Значение коллекторного тока в АР определяется формулой (3.11) IК = aIЭ + IКБО. Выходные характеристики смещаются вверх при увеличении тока эмиттера IЭ. В идеализированном транзисторе не учитывается эффект Эрли (уменьшение ширины базовой области), поэтому интегральный коэффициент передачи тока a можно считать постоянным, не зависящим от значения |UКБ|. Следовательно, в идеализированном БТ выходные характеристики оказываются горизонтальными (IК = const). Реально же эффект Эрли при росте |UКБ| приводит к уменьшению потерь на рекомбинацию в базе и росту a. При этом незначительно увеличивается выходная проводимость. Так как значение a близко к единице, то относительное увеличение очень мало и может быть обнаружено только измерениями. Поэтому отклонение выходных характеристик от горизонтальных линий вверх «на глаз» не заметно (на рисунке 3.5, б масштаб не соблюдается).
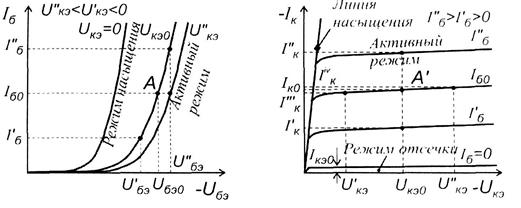
Схема с общим эмиттером
Семейство входных характеристик схемы с ОЭ представляет собой зависимости IБ = f(UБЭ), причем заданным параметром является напряжение UКЭ (рисунок 3.6, а). Для p-n-p-транзистора отрицательное напряжение UБЭ (UБЭ 0.
Если при этом UКЭ = 0 (потенциалы коллектора и эмиттера одинаковы), то и коллекторный переход будет включен в прямом направлении: UКБ=UКЭ+UЭБ= = UЭБ > 0. Поэтому входная характеристика при UКЭ = 0 будет соответствовать режиму насыщения (РН), а ток базы будет равным сумме базовых токов из-за одновременной инжекции дырок из эмиттера и коллектора. Этот ток, естественно, увеличивается с ростом прямого напряжения UЭБ, так как оно приводит к усилению инжекции через оба перехода (UКБ = UЭБ) и соответствующему возрастанию потерь на рекомбинацию, определяющих базовый ток.
Вторая характеристика на рисунке 3.6, а (UКЭ IКБ0 и IБ меняет направление и становится положительным (IБ > 0) и сильно зависящим от напряжения перехода.
Влияние UКЭ на IБ в активном режиме можно объяснить тем, что рост |UКЭ| означает рост |UКБ| и, следовательно, уменьшение ширины базовой области (эффект Эрли). Последнее будет сопровождаться снижением потерь на рекомбинацию, т.е. уменьшением тока базы (смещение характеристики незначительно вниз).
Семейство выходных характеристик схемы с ОЭ представляет собой зависимости IК = f(UКЭ) при заданном параметре IБ (рисунке 3.6, б).
Наклон выходных характеристик в нормальном активном режиме в схеме с общим эмиттером во много раз больше, чем в схеме с общей базой (h22Э » bh22Б) Объясняется это различным проявлением эффекта Эрли. В схеме с общим эмиттером увеличение UКЭ, а следовательно и UКБ, сопровождается уменьшением тока базы, а он по определению выходной характеристики должен быть неизменным. Для восстановления тока базы приходится регулировкой напряжения UБЭ увеличивать ток эмиттера, а это вызывает прирост тока коллектора DIК, т.е. увеличение выходной проводимости (в схеме с ОБ ток IЭ при снятии выходной характеристики поддерживается неизменным).
Влияние температуры на статические характеристики БТ
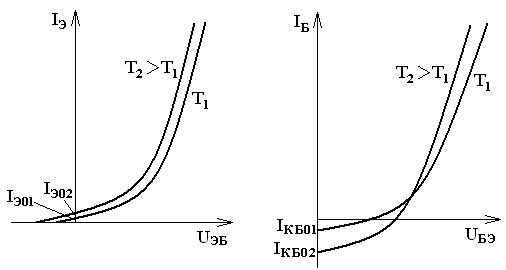
Влияние температуры на положение входной характеристики схемы с ОБ при поддержании неизменным напряжения коллектор-база аналогично влиянию температуры на ВАХ полупроводникового диода. В нормальном активном режиме ток эмиттерного перехода можно представить формулой
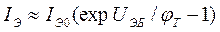
С ростом температуры тепловой ток IЭ0 растет быстрее, чем убывает экспонента из-за увеличения jТ = kT/q. В результате противоположного влияния двух факторов входные характеристики схемы с ОБ смещаются влево при выбранном токе IЭ на величину DU » (1. 2) мВ/°С (рисунок 3.7, а).
| а) | б) |
| Рис. 3.7. Зависимость входных характеристик от температуры: а) для схем ОБ; б) для схем ОЭ |
Начало входной характеристики в схеме с ОЭ определяется тепловым током коллекторного перехода IКБО который сильно зависит от температуры, так что начало характеристики при увеличении температуры опускается (рисунок 3.7, б). При больших значениях тока базы характеристики ведут себя по тем же причинам так же, как и в схеме с ОБ.
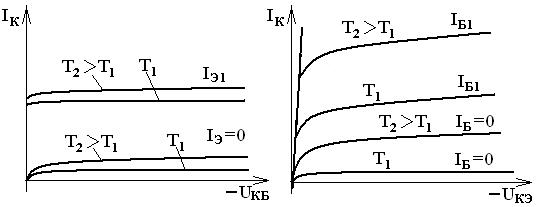
Влияние температуры на выходные характеристики схем с ОБ и ОЭ в АР удобно анализировать по формулам (3.11) и (3.22):
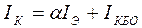
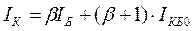
Снятие выходных характеристик при различных температурах должно проводиться при поддержании постоянства параметров (IЭ = const в схеме с ОБ и IБ = const в схеме с ОЭ). Поэтому в схеме с ОБ при IЭ = const рост IК будет определяться только увеличением IКБО (рисунок 3.8, а).
Однако обычно IКБО значительно меньше aIЭ, изменение IК составляет доли процента и его можно не учитывать.
В схеме с ОЭ положение иное. Здесь параметром является IБ и его надо поддерживать неизменным при изменении температуры. Будем считать в первом приближении, что коэффициент передачи b не зависит от температуры. Постоянство произведения (b∙IБ) означает, что температурная зависимость IК будет определяться слагаемым (b + 1)IКБО. Ток IКБО (как тепловой ток перехода) примерно удваивается при увеличении температуры на 10°С, и при b >> 1 прирост тока (b + 1)IКБО может оказаться сравнимым с исходным значением коллекторного тока и даже превысить его.
| а) | б) |
| Рис. 3.8. Зависимость выходных характеристик БТ от температуры. а) для схем включения с ОБ; б) для схем включения ОЭ |
На рис. 3.8, б показано большое смещение выходных характеристик вверх. Сильное влияние температуры на выходные характеристики в схеме с ОЭ может привести к потере работоспособности конкретных устройств, если не принять схемотехнические меры для стабилизации тока или термостатирование.
Тема 4. Биполярные транзисторы



Биполярный транзистор – полупроводниковый прибор, образованный двумя последовательно включенными взаимодействующими p-n-переходами и содержащий три или более вывода, усилительные свойства которого обусловлены явлениями инжекции и экстракции носителей заряда. Процессы усиления в БТ объясняются возможностью управления большим током в выходной цепи ( коллектор или эмиттер) при небольших изменениях напряжения или тока во входной цепи ( эмиттер- база).
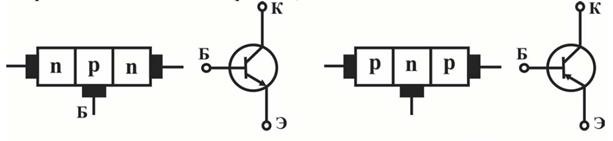
В зависимости от порядка чередования областей полупроводника, различают транзисторы а) р-n-р-типа и б) n-р-n-типа ( рис.4.1.)
Отличие между ними заключается в различной полярности источников внешних напряжений и в направлении протекания токов через электроды при одинаковом принципе работы. Эмиттером называется одна из крайних областей, которую легируют сильнее, что позволяет использовать ее в режиме инжекции. Промежуточную область называют базой а другую крайнюю область – коллектором. В область коллектора производится экстракция носителей заряда из базовой области. Электронно-дырочный переход между эмиттерной и базовой областями называют эмиттерным, а между коллекторной и базовой – коллекторным.
В зависимости от напряжения на переходах возможны следующие режимы работы транзистора:
режим отсечки – на обоих переходах обратное напряжение;
режим насыщения – на обоих переходах прямое напряжение;
инверсный режим – обратный по отношение к активному, то есть коллекторный переход смещен в прямом направлении, эмиттерный – в обратном.
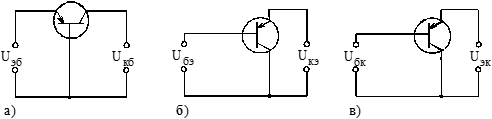
В зависимости от того, какой из выводов транзистора является общим для входной и выходной цепи, различают три схемы включения транзистора: с общей базой (ОБ), с общим эмиттером (ОЭ) и с общим коллектором (ОК). На рис. 4.2. показаны полярности внешних источников напряжения и направления токов транзистора, соответствующие активному режиму работы, для трех схем включения.
Рис. 4.2. Схемы включения биполярного транзистора ( ОБ,ОЭ,ОК)
С ростом прямого смещения Uэб на эмиттерном переходе происходит уменьшение его потенциального барьера, что вызывает инжекцию дырок из эмиттера в базу и электронов из базы в эмиттер.
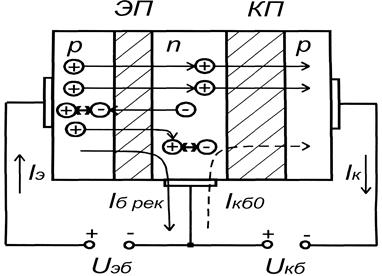
Рис.4.3. Внутренняя структура биполярного транзистора
При этом, как и ранее в полупроводниковых диодах, используется несимметричный р-п переход, при котором концентрация примеси в эмиттере много больше концентрации примеси в базе (концентрация основных носителей эмиттера много больше концентрации основных носителей базы). Это приводит к тому что инжекция дырок из эмиттера в базу преобладает над инжекцией электронов из базы в эмиттер. Ток инжекции имеет две составляющие: дырочную Iэp и электронную Iэn. Процесс инжекции характеризуется коэффициентом инжекции (эффективностью эмиттерного перехода) 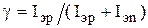
В результате инжекции происходит диффузия дырок через базу к коллекторному переходу. Этот процесс усиливается тем, что дырки, подошедшие к обратносмещенному коллекторному переходу, попадают в его ускоряющее поле Uкб и экстрагируют в коллектор, создавая управляемую составляющую тока коллектора Iк упр..
По мере продвижения по базе незначительная часть дырок рекомбинирует с собственными носителями базы – электронами, создавая рекомбинационную составляющую тока базы Iб рек. Коэффициент переноса неосновных носителей через базу характеризуется e = Iкp/Iэp, где Iкp – ток дырок, дошедших до коллекторного перехода в области базы.
При экстракции может также происходить ударная ионизация атомов полупроводника и лавинное умножение носителей заряда в коллекторном переходе, которое оценивается коэффициентом лавинного умножения М = Iк упр/Iкp. Произведение частичных коэффициентов передачи позволяет определить сквозной коэффициент передачи по току в схеме с ОБ (статический коэффициент передачи тока эмиттера) как 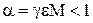
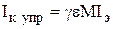
Значения параметра 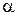
Можно заметить, что в общем случае при малой ширине базы поле КП полностью формирует ток коллектора, то есть напряжение на коллекторном переходе при этом может отсутствовать. Однако в реальной схеме включения БТ напряжение Uкэ всегда имеется, что обусловлено включением нагрузки и необходимостью создания выходного тока в цепи коллектора.
Следовательно, кроме управляемого тока коллектора 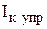
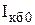
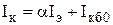
Обратный неуправляемый ток сильно зависит от температуры, поэтому 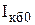
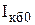
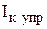
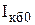
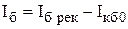
Величина 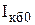
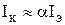
Для БТ можно записать так называемое внутреннее уравнение транзистора, то есть выражение, связывающее токи всех трех выводов БТ:
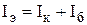
Выражение, связывающее выходной 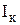
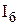
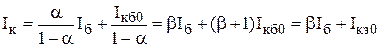
Параметр 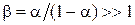
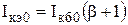
Коэффициент 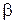
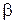
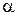
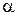
В активном режиме работы токи коллектора и эмиттера БТ практически равны, а незначительный ток базы равен их разности.
Это приводит к тому, что в схеме с ОБ отсутствует усиление по току ( 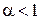
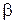
Усиление входного сигнала по напряжению и мощности возможно получить в обеих рассмотренных схемах включения ( ОБ и ОЭ). Поскольку ток коллектора формируется без участия Uк, величина коллекторного тока практически не зависит от напряжения на коллекторном переходе, поэтому дифференциальное сопротивление коллекторного перехода 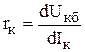
В связи с этим в цепь коллектора можно включать нагрузку с большим сопротивлением 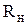
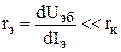
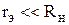
Можно увидеть, что изменение входного (эмиттерного) тока на величину 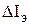
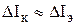
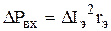
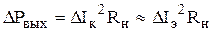
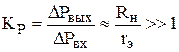
Аналогичные выводы можно получить и для схемы с ОЭ, которая является универсальной ( то есть усиливает и по току и по напряжению и по мощности). Для схемы включения с ОК можно определить соотношение выходного тока эмиттера и входного тока базы как
Кi =Iэ/Iб=(Iк+ Iб)/Iб= (1+ 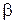
Статические ВАХ отражают зависимости между постоянными входными и выходными токами и напряжениями транзистора. Для любой схемы включения транзистора можно получить четыре семейства статических ВАХ: входные 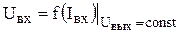
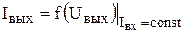
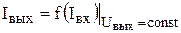
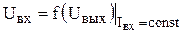
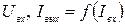
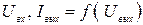
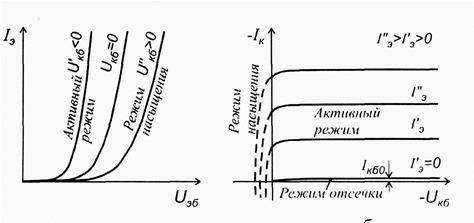
На рис. 4.3. и рис 4.4.. приведены графики семейств статических ВАХ транзистора, имеющего p-n-p-структуру, для включения с ОБ.
Рис 4.4. Входные и выходные статические ВАХ p-n-p-транзистора с ОБ.
Входные характеристики представляют собой известные характеристики прямосмещенного р-п перехода. Выходные характеристики позволяют оценить поведение транзистора в различных режимах работы в соответствии с определением режимов.
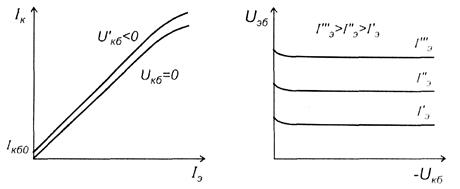
Рис.4.5. Характеристики прямой передачи и обратной связи БТ с ОБ
Характеристики прямой передачи БТ являются линейными в рабочей области входных токов в соответствии с уравнением 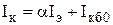
Поведение характеристик обратной связи объясняется эффектом модуляции ширины базы в области небольших значений U кб.
Для схемы включения БТ с ОЭ поведение входных характеристик ( рис. 4.6.) объясняется так же как и для схемы с ОБ. На выходных характеристиках требует пояснения отличное от схемы с ОБ расположение области режима насыщения
Рис.4.6. Входные и выходные характеристики БТ с ОЭ
В частности в схеме с ОЭ насыщение БТ наступает при выполнении условия Uкэ