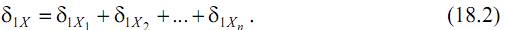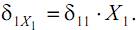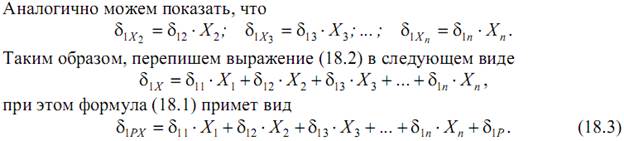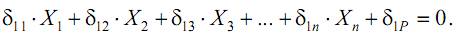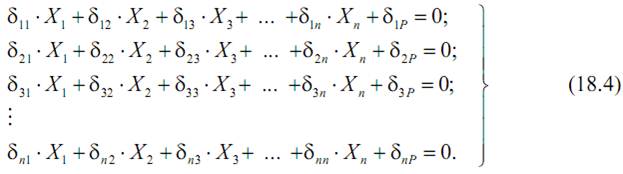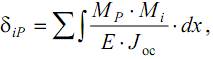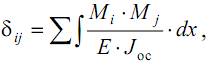Что такое статически неопределимая система

Статически неопределимая система

Полезное

Смотреть что такое «Статически неопределимая система» в других словарях:

Статически неопределимая система — в строительной механике, геометрически неизменяемая система, в которой реакции связей (усилия в опорных закреплениях, стержнях и т. п.) не могут быть определены с помощью одних уравнений статики, а требуется совместное рассмотрение… … Википедия

СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СИСТЕМА — (в строительной механике) геометрически неизменяемая система, в которой для определения всех реакций связей (усилий в опорных закреплениях, стержнях и т. п.) необходимы, помимо уравнений статики, дополнительные уравнения, характеризующие… … Большой Энциклопедический словарь

статически неопределимая система — (в строительной механике), геометрически неизменяемая система, в которой для определения реакций связей (усилий в опорных закреплениях, стержнях и т. п.) необходимы, помимо уравнений статики, дополнительные уравнения, характеризующие деформации… … Энциклопедический словарь

СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ СИСТЕМА — в строительной механике геометрически неизменяемая система, в к рой для определения усилий во всех элементах и опорных связях необходимы, помимо ур ний статики, дополнит. ур ния, характеризующие деформации системы … Большой энциклопедический политехнический словарь

Статически определимая система — в строительной механике, система конструкций, в которой реакции всех связей (усилия в опорных закреплениях, стержнях и т.п.) при любой нагрузке могут быть определены с помощью уравнений статики (см. Строительная механика). С. о. с.… … Большая советская энциклопедия

Статически определимая система — Статическая система называется статически определимой, если число опорных реакций соответствует числу степеней свободы, и величины опорных реакций по принципу механического равновесия можно определить из величин внешних нагрузок. Все другие… … Википедия

система статически неопределимая — статически неопределимая система Геометрически неизменяемая, система, содержащая связи, реакции которых при произвольной статической нагрузке могут быть найдены лишь из совместного рассмотрения условий статики и условий, характеризующих… … Справочник технического переводчика

СИСТЕМА СТАТИЧЕСКИ НЕОПРЕДЕЛИМАЯ — конструктивная система, количество наложенных связей в которой превышает число уравнений статического равновесия (Болгарский язык; Български) статически неопределима система (Чешский язык; Čeština) staticky neurčitá soustava (Немецкий язык;… … Строительный словарь

Система, статически неопределимая — геометрически неизменяемая система, содержащая связи, реакции которых при заданной нагрузке могут быть найдены лишь при совместном рассмотрении условий статики и условий, характеризующих деформацию данной системы. Источник: Справочник дорожных… … Строительный словарь

Ферма (технич.) — Ферма (франц. ferme, от лат. firmus √ крепкий, прочный), несущая конструкция, состоящая из прямолинейных стержней, узловые соединения которых при расчёте условно принимаются шарнирными. Ф. применяют главным образом в строительстве (покрытия… … Большая советская энциклопедия

Источник

СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ

18.1. Общие понятия и определения

Статически неопределимая система – это конструкция, силовые факторы в элементах которой невозможно определить только из уравнений равновесия (уравнений статики).

Статическая неопределимость возникает в том случае, когда число наложенных на систему связей оказывается больше, чем это необходимо для обеспечения ее равновесия. При этом некоторые из этих связей становятся как бы «лишними», а усилия в них – лишними неизвестными. По числу лишних неизвестных устанавливают степень статической неопределимости системы. Отметим, что термин «лишние» связи является условным, так как эти связи необходимы для обеспечения прочности и жесткости системы, хотя и «избыточны» с точки зрения ее равновесия.

Связь – условие закрепления или соединения элементов конструкции, не допускающее изменения их взаимного положения (внутренние связи) и положения в пространстве (внешние связи).

До сих пор мы рассматривали простейшие статически неопределимые системы, элементы которых работали только на растяжение (сжатие). Такие конструкции обычно называют фер м ами. Ферма– конструкция, состоящая из прямых стержней, соединенных между собой шарнирами, и нагруженная силами, приложенными в узлах (в шарнирах).

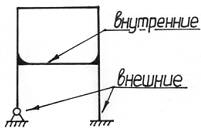
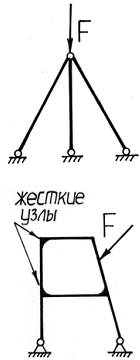
Далее рассмотрим более общие случаи статически неопределимых систем, элементы которых могут находиться в условиях сложного сопротивления, испытывать изгиб, кручение и т. д. Наиболее распространенным примером таких конструкций являются рамы.

Рама – конструкция, состоящая из стержней произвольной конфигурации и имеющая один или несколько жестких (не шарнирных) узлов.

Как рамы, так и фермы могут быть а) плоскими – все элементы конструкции и силы лежат в одной плоскости; б) плоскопространственными – все элементы конструкции лежат в одной плоскости, а силы перпендикулярны к этой плоскости; в) пространственными – элементы конструкции и силы располагаются произвольно друг относительно друга.

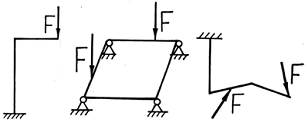
В общем случае нагружения статически неопределимой системы наиболее эффективными способами определения деформаций ее элементов являются энергетические методы, возможности применения которых рассмотрим в следующем параграфе.

18.2. Метод сил. Основная идея метода

Для того чтобы обратить заданную статически неопределимую систему в статически определимую, в методе сил используется следующий прием. Все «лишние» связи, наложенные на конструкцию, отбрасываются, а их действие заменяется соответствующими реакциями – силами или моментами. При этом, для сохранения заданных условий закрепления и нагружения, реакции отброшенных связей должны иметь такие значения, при которых перемещения в направлении этих реакций равнялись бы нулю (или заданным величинам).

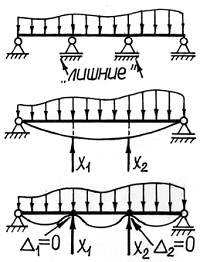
Таким образом, при раскрытии статической неопределимости этим методом

искомыми оказываются не деформации, а соответствующие им силы – реакции связей (отсюда и название «метод сил»).

Запишем основные этапы раскрытия статической неопределимости по методу сил:

1) определяем степень статической неопределимости системы, то есть число лишних неизвестных;

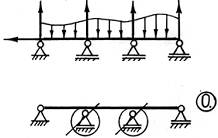
Заметим, что выбор лишних связей может быть достаточно произвольным и зависит лишь от желания расчетчика, так что для одной и той же исходной статически неопределимой системы возможны различные варианты основных систем. Однако нужно следить за тем, чтобы основная система оставалась геометрически неизменяемой – то есть ее элементы после удаления лишних связей не должны иметь возможности свободно перемещаться в пространстве.

3) составляем уравнения для деформаций в точках приложения лишних неизвестных. Так как в исходной системе эти деформации равны нулю, то и указанные уравнения необходимо также приравнять к нулю. Затем из полученных уравнений находим величину лишних неизвестных.

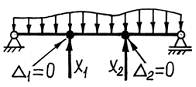
18.3. Канонические уравнения метода сил

Рассмотрим балку, загруженную произвольной системой сил, на которую наложено n «лишних» связей – система n раз статически неопределима.

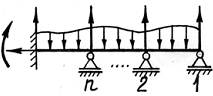
Для раскрытия статической неопределимости используем метод сил.

1) Освободим балку от лишних связей и получим вид основной системы. Далее все рассуждения будем проводить применительно к основной системе.

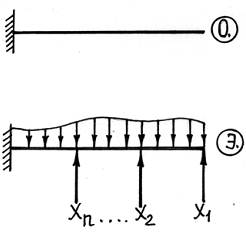
Эквивалентная система – система, полученная из основной, после ее загрузки внешними силами и лишними неизвестными.

3) Рассмотрим деформации эквивалентной системы (например, в точке 1). Под действием внешних нагрузок (P) и лишних неизвестных (X) точка 1 сместится на некоторую величину δ1PX. Согласно принципу независимости действия сил, эта деформация может быть найдена как сумма двух деформаций – деформации балки только под действием внешних сил δ1P и деформации балки под действием лишних неизвестных δ1X

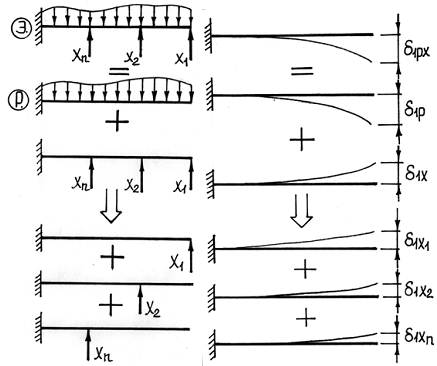
Проанализируем перемещение δ1X точки 1 под действием лишних неизвестных (X1, X2,…, Xn). Каждая из лишних неизвестных (X1, X2,…, Xn) сама по себе вызовет некоторую деформацию балки 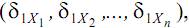при этом сумма таких деформаций и составит в итоге полную деформацию балки от лишних неизвестных

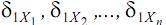
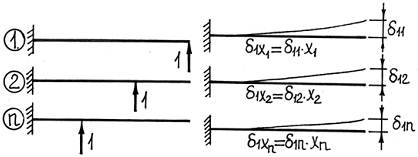
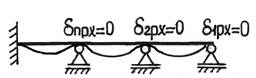
Для определения деформаций используем следующий искусственный прием. Приложим к основной системе вместо лишних неизвестных (X1, X2,…, Xn) известные единичные силы (силы, величина которых равна единице), обозначим их 1, 2, 3,…, n.

Каждая единичная сила в отдельности сдеформирует балку на некоторую величину (δ11, δ12,…, δ1n). Так как неизвестная X1 отличается от единичной силы 1 в X1 раз, то и деформации, вызванные этими силами, будут отличаться в X1 раз в силу линейной связи (закон Гука!) между деформациями и усилиями, то есть

4) Так как в точке 1 исходной системы была установлена опора (лишняя связь), то для сохранения эквивалентности исходной и рассматриваемой систем необходимо потребовать, чтобы перемещение в этой точке равнялось нулю, то есть δ1PX=0, или, с учетом (18.3)

Подобные рассуждения можем провести для каждой точки исходной системы, где установлена опора (лишняя связь). В итоге получим следующую систему уравнений:

5) Определим коэффициенты δ, входящие в уравнения (4).

Коэффициент δiP есть перемещение i-ой точки основной системы под действием внешних сил (P). Для его определения можно воспользоваться методом Максвелла-Мора, учитывая все участки конструкции

где MP – внутренний изгибающий «грузовой» момент (определяется по «грузовой» системе, то есть системе, нагруженной только внешними силами); Mi – внутренний изгибающий «единичный» момент (определяется по «единичной» системе, то есть системе, нагруженной только единичной силой, приложенной в i-ой точке).

Коэффициент δij есть перемещение i-ой точки основной системы под действием j-ой единичной силы. Для его определения можно также воспользоваться методом Максвелла-Мора с учетом всех участков системы

где Mi – внутренний изгибающий «единичный» момент (определяется по i-ой «единичной» системе, то есть системе, нагруженной только единичной силой, приложенной в i-ой точке); Mj – внутренний изгибающий «единичный» момент (определяется по j-ой «единичной» системе, то есть системе, нагруженной только единичной силой, приложенной в j-ой точке).

Таким образом, для определения коэффициентов δ необходимо определить внутренние изгибающие моменты для нескольких систем: одной «грузовой», загруженной только внешними силами, и несколькими «единичными», каждая из которых загружается всего лишь одной силой – единичной силой, приложенной по направлению и в той точке, где ищется лишняя неизвестная (X). Затем эти внутренние усилия необходимо подставить в интеграл Максвелла-Мора и найти δ.

18.4. Учет симметрии при расчете статически неопределимых систем

Можно значительно упростить систему канонических уравнений метода сил, если есть возможность учесть симметрию конструкции и приложенных к ней нагрузок, поскольку при этом некоторые побочные коэффициенты канонических уравнений оказываются равными нулю.

Симметричнойбудем называть конструкцию, если одна из ее частей является зеркальным отражением второй части относительно плоскости (оси) симметрии.

Усилия (и внешние, и внутренние), действующие на симметричную конструкцию, можно разделить на симметричные и кососимметричные.

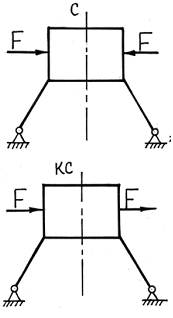
Симметричной будем считать нагрузку, если усилия, приложенные к одной части конструкции, являются зеркальным отображением усилий, приложенных к другой ее части.

Кососимметричной будем считать нагрузку, если усилия, приложенные к одной части конструкции, являются зеркальным отображением усилий, приложенных к другой ее части, но взятых с противоположным знаком.

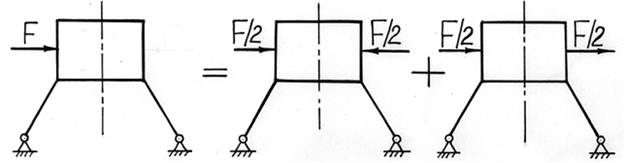
Заметим, что любую несимметричную нагрузку, приложенную к симметричной конструкции, можно разложить на две составляющие, одна из которых будет симметричной, а другая – кососимметричной. Полученные две задачи решаются затем с учетом симметрии, а результаты суммируются.

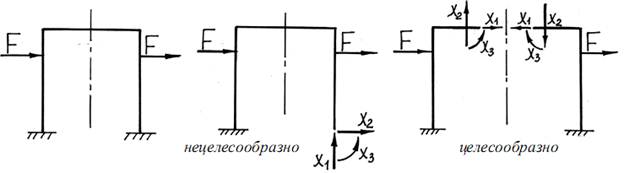
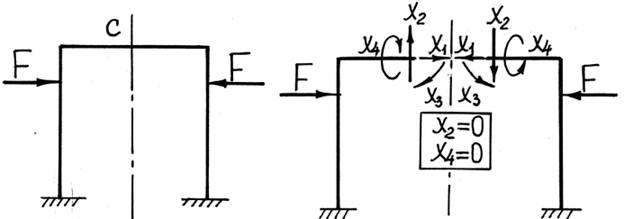
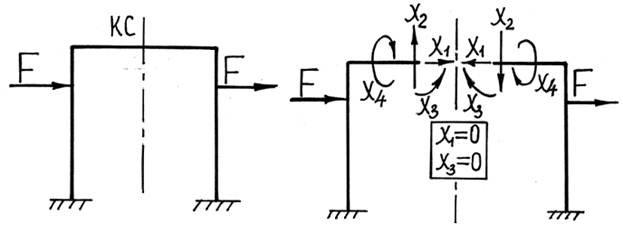
Особенностью, упрощающей решение статически неопределимых задач с учетом симметрии, является тот факт, что в качестве лишних неизвестных здесь целесообразно выбирать не реакции опор, а внутренние усилия, расположенные в плоскости симметрии конструкции.

При этом искомые внутренние усилия можно будет также подразделить на симметричные и кососимметричные: осевое усилие N и изгибающие моменты My, Mz – симметричные силовые факторы, а поперечные силы Qy, Qz и крутящий момент Mx –кососимметричные.

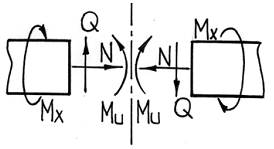
При анализе симметричных конструкций удобно использовать следующие правила:

1) в симметричной конструкции при симметричной внешней нагрузке в плоскости симметрии равны нулю кососимметричные внутренние усилия (Q, Mx);

2) в симметричной конструкции при кососимметричной внешней нагрузке в плоскости симметрии равны нулю симметричные внутренние усилия (N, My, Mz).

После того как путем решения системы канонических уравнений найдены неизвестные «лишние» усилия X1, X2,…, Xn, эти усилия и заданную нагрузку можно приложить к основной системе (получим эквивалентную статически определимую систему). Затем от их совместного действия обычным способом можно определить внутренние усилия по участкам системы, построить их эпюры и провести расчет на прочность.

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Статически неопределимые системы

Вы будете перенаправлены на Автор24

Сущность статически неопределимых систем

Статически неопределимая система – это геометрически неизменяемая система, в которой усилия в опорах, стержнях и т.д. не могут определяться с помощью одних лишь уравнений статики. Такие системы требуют совместное рассмотрение статических уравнений равновесия совместно с дополнительными уравнениями, которые характеризуют деформации системы.

Статически неопределимая система характеризуется наличием «лишних» связей, которые допускается удалить, не нарушив при этом геометрической неизменяемости системы. Количество дополнительных уравнений, которые следует составить для определения усилий, будет равно числу «лишних» связей (лишних неизвестных). Данное число еще называют степенью статической неопределимости системы, о ней также пойдет речь в настоящей статье. Для определения усилий в подобных системах чаще всего используют метод сил и метод перемещений. Метод сил также используется при механизированном расчете строительных конструкций.

Из вышеизложенного следует, что степень статической неопределимости системы может быть найдена по формуле:

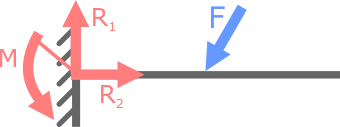
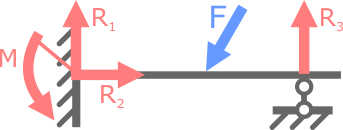
В качестве примера можно рассмотреть случай с заделанной с одной стороны консольной балкой. Поскольку в такой опоре существует три опорные реакции, данная система будет являться статически определимой, ведь из курса теоретической механики известно, что для плоской системы сил можно составить только три уравнения равновесия.

Если добавить к вышеописанной системе еще одну опору, например, шарнирно-подвижную, то такая балка становится статически неопределимой один раз, поскольку количество неизвестных увеличивается до четырех, а уравнений равновесия для данного случая можно составить только три.

Готовые работы на аналогичную тему

Таким образом, если к рассматриваемой системы прибавлять последовательно по одной опоре, то степень статической неопределимости также будет увеличиваться на единицу. В таких случаях для определения величины и направления неизвестных усилий потребуется составление дополнительных уравнений.

Процесс определения усилий в «лишних» связях системы называют раскрытием статической неопределимости. Существует ряд способов раскрытия статической неопределимости, их принцип основан на двух положениях. Первое основано на равенстве нулю соответствующих точек системы на ее опорах, второе – на совместности деформаций всех или нескольких элементов системы.

Степень статической неопределимости

Следует заметить, что перед расчетом любой системы методами строительной механики необходимо определить степень статической неопределимости этой системы. Как уже упоминалось выше, для простейших систем (балок и элементарных рам) степень статической неопределимости будет равна числу «лишних» связей.

Дополнительные связи в системах можно удалить, не нарушив при этом их геометрической неизменяемости. Особенностью большинства этих связей является то, что реакции от внешних усилий в них определить нельзя с помощью одних лишь уравнений статики. Такие связи называют условно необходимыми. Наряду с ними в системах часто имеются связи, усилия в которых можно определить из условий равновесия. Такие связи называют абсолютно необходимыми. Удаление этих связей приводит к преобразованию системы в геометрически неизменяемую или мгновенно изменяемую.

Следует различать внешне и внутренне статически неопределимые системы. Первые представляют собой системы, в которых имеются только «лишние» внешние связи (например, опорные закрепления). Внутренне статически неопределимыми называют системы, обладающие «лишними» связями, которые обычно вводятся для взаимного соединения частей системы.

Однако, для определения степени статической неопределимости сложной системы следует понимать разницу между простым и сложным шарниром. Простым называют шарнир, соединяющий два стержневых элемента. Шарнир, соединяющий три и более стержня, называют сложным. Количество простых шарниров в системе можно определить по формуле:

Ш = СТ – 1,

где СТ – количество стержневых элементов в узле.

Источник

iSopromat.ru

Статически неопределимыми называют системы, в которых для определения опорных реакций либо внутренних усилий одних только уравнений статики недостаточно.

Статическая неопределимость возникает из-за наличия дополнительных или «лишних» связей.

Здесь под словом «лишние» понимаются дополнительные опоры (связи) добавление которых не влияет на геометрическую неизменяемость системы в целом.

Дополнительные опоры увеличивают прочность и жесткость систем, что позволяет делать их более экономичными.

Степень статической неопределимости систем

Степень статической неопределимости n определяется по формуле:

где,
k – количество неизвестных усилий (реакций связи),
m – количество уравнений равновесия которые можно составить для данной системы.

Системы, для которых n=1 называют однажды статически неопределимыми, n=2 – дважды СН и т.д.

Примеры статически неопределимых систем

В качестве примера рассмотрим следующий случай:

Консольная балка, закрепленная только в жесткой заделке – статически определима, так как в опоре данной схемы могут иметь место не более трех опорных реакций (вертикальная и горизонтальная силы и момент).

Как известно из курса теоретической механики для плоской системы сил можно составить только три уравнения равновесия. Трех уравнений для определения трех неизвестных вполне достаточно.

Теперь, если добавим к рассматриваемой схеме еще одну опору, например шарнирно-подвижную, то балка становится статически неопределимой, так как количество неизвестных связей увеличилось до четырех, а уравнений равновесия по-прежнему можно составить только три.

В данном случае для расчета опорных реакций не хватает еще одного уравнения, т.е. система один раз (однажды) статически неопределима.

Если к данной системе последовательно добавлять опоры, то степень неопределимости также будет возрастать.

В таких случаях для расчета величины и направления неизвестных усилий потребуются дополнительные уравнения.

Другие примеры СНС

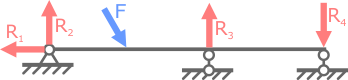
Примеры однажды статически неопределимых систем (n=1):

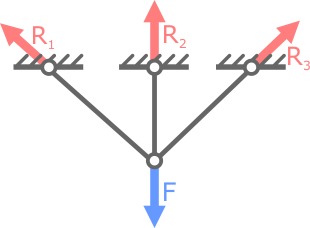
Статически неопределимая стержневая система

Раскрытие статической неопределимости

Расчет усилий в лишних связях называется раскрытием статической неопределимости системы.

Существует несколько способов раскрытия статической неопределимости, принцип которых основан на:

Наиболее универсальным из них является метод сил.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Понятие о статически неопределимых системах

Статически неопределимой называется система, внутренние усилия которой нельзя определить только из уравнений статики (равновесия). Статически неопределимые системы (СНС) отличаются от статически определимых рядом свойств:

1. Они надежнее, разрушение некоторых элементов не всегда приводит к разрушению всей системы.

2. Они выдерживают бо́льшую нагрузку.

3. У них деформации меньше.

4. Изменение температуры, смещение опор, неточность изготовления элементов вызывают дополнительные усилия.

5. Внутренние усилия зависят от физических и геометрических характеристик элементов.

У статически неопределимых систем есть так называемые «лишние» связи, число которых называется степенью статической неопределимости. Степень статической неопределимости n простой системы определяется из дискового аналога по следующей формуле:

.

Например, степени статической неопределимости балки (рис. 7.1 а) и рамы (рис. 7.1 в) будут:

Использование этой формулы при расчете сложных рам затруднительно. Поэтому можно применить другой подход, вводя два понятия: 1) замкнутый контур – замкнутая цепь из элементов и связей системы; 2) удалённая связь – связь замкнутого контура, исключенная из жесткого соединения элементов (см. рис. 7.1 б, г, е).

Степень статической неопределимости сплошного замкнутого контура равняется трем. Поэтому степень статической неопределимости системы из n_к замкнутых контуров, из которых удалены n_уд связей, будет

При использовании этой формулы для балки (рис. 7.1 а) и рам (рис. 7.1 в, д) в этих системах необходимо определить общее число замкнутых контуров n_к и удаленных связей n_уд (рис. 7.4 б, г, е). Тогда

Степень статической неопределимости фермы определяется по формуле

n= n_С+ n –2n_У .

Например, для фермы (рис. 7.1 ж): n=6+3–2×4=1.

Выбор основной системы

Расчет статически неопределимой системы начинается с превращения ее в статически определимую. Для этого необходимо исключить лишние связи и заменить их реакции неизвестными силами. Полученная система называется основной системой (ОС).

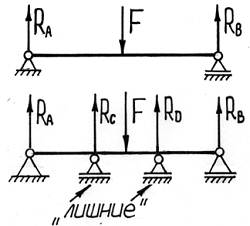
Например, у балки (рис. 7.2 а), которую далее будем называть заданной системой (ЗС), степень статической неопределимости n=1. Если исключить лишнюю связь (правую опору) и обозначить неизвестную реакцию через X, получим ее ОС (рис. 7.2 б).

Способов исключения лишних связей очень много (теоретически – бесконечное число). Например, лишнюю связь можно исключать как на рис. 7.2 в-е. Однако одна из этих схем (рис. 7.2 е) геометрически изменяема и для дальнейшего расчета непригодна. Все остальные схемы могут быть приняты за основную систему.

Если воспользоваться известным теоретическим положением о том, что в линейно-упругих системах внешняя нагрузка распределяется единственным образом, то результаты расчетов по различным ОС должны быть одинаковыми. Однако объем вычислений в разных ОС может быть разным. Поэтому из многих вариантов ОС нужно выбирать наиболее оптимальную. Например, в нашем примере первый вариант ОС (рис. 7.2 б) предпочтительнее остальных, т.к. в ней эпюры строятся легче.

Итак, основная система должна быть:

1) обязательно геометрически неизменяемой;

2) простой для расчета;

3) учитывать особенности сооружения и действующей нагрузки.

Сущность метода сил

В рассматриваемом методе расчета статически неопределимых систем за основные неизвестные принимаются силы (внутренние усилия). Поэтому он и называется методом сил.

Изучим метод сил на примере предыдущей балки (рис. 7.2 а).

Потребуем, чтобы ее ЗС (рис. 7.2 а) и ОС (рис. 7.2 б) были эквивалентными. Для этого перемещение в направлении исключенной связи должно равняться нулю:

По принципу суперпозиции, это перемещение равно сумме перемещения D_X (рис. 7.3 а) от неизвестной реакции X и перемещения D_P (рис. 7.3 б) от заданной силы P. Поэтому

Это уравнение, учитывающее геометрические особенности системы, называется уравнениемсовместности деформаций.

Так как сила X неизвестна, перемещение D_X непосредственно определить нельзя. Поэтому рассмотрим единичное состояние (ЕС) основной системы, где действует только единичная сила P=1 (рис. 7.3 в). Перемещение d, возникающее в нем в направлении единичной силы, называется податливостью, и его уже можно определить.

По закону Гука, в линейно-упругой системе D_X=d X. Тогда последнее уравнение принимает вид

= + +×××+ +D_1P=0,

= + +×××+ +D_2P=0,

D_n= + +×××+ +D_nP =0.

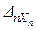
При рассмотрении n различных единичных состояний системы и определении податливостей по различным направлениям эти уравнения приводятся к системе уравнений:

+ X₂+×××+ X_n+D _P=0,

+ X₂+×××+ X_n+D_2P=0,

+ X₂+×××+ X_n+D_nP=0.

Она называется системой канонических уравнений метода сил. Здесь – главные коэффициенты, – боковые коэффициенты. Свободные члены D_iP называются грузовыми коэффициентами.

Систему с большим количеством уравнений необходимо решать на компьютере. С этой целью введем матричные обозначения:

d= ; X = ;D_P = ; 0 = ,

где d – матрица податливости, X – вектор неизвестных, D_P – вектор нагрузки, 0 – нуль-вектор. В результате этого система канонических уравнений принимает вид:

d X +D_P = 0.

Из этого матричного уравнения определяется вектор неизвестных:

X =–d –1 D_P.

Здесь d –1 – обратная матрица податливости.

Источник