Что такое степень двойки в информатике

Степени двойки

Этот вспомогательный материал, который может быть полезен для подготовки к ГИА по информатике, в частности задач 15 ГИА, задач 1 ГИА, B10 ЕГЭ по информатике

Степени двойки таблица

2 0	1
2 1	2
2 2	4
2 3	8
2 4	16
2 5	32
2 6	64
2 7	128
2 8	256
2 9	512
2 10	1024
2 11	2048
2 12	4096
2 13	8192
2 14	16384
2 15	32768
2 16	65536
2 17	131072
2 18	262144
2 19	524288
2 20	1048576

Автор: Александр Чернышов

Оцените статью, это очень поможет развитию сайта.

Источник

Двоичная система для чайников

Я решил сделать серию постов по информатике для чайников.

Если первый пост пойдёт хорошо, то будет еще несколько в том же духе.

Чтобы провести хирургическую операцию, анатомию знать не обязательно, но вот результаты будут непредсказуемы. Точно так же, чтобы программировать, не обязательно знать, как компьютер устроен изнутри, но иногда такое незнание может привести к душераздирающим последствиям.

Основа основ современного компьютера – ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ (2-СС). Звучит угрожающе. Чтобы понять, что такое ДСС, и научиться с ней работать, надо уметь складывать, умножать и возводить числа в степень. Ок, даю шпаргалку.

Пусть у нас есть какое-то число. Допустим, 5. И мы хотим прибавить к нему другое число. Допустим, 3. Как нам это сделать? Давайте, представим число 5 как пять палочек:

А число 3 как три палочки:

Чтобы сложить их, сначала нарисуем пять палочек, потом допишем к ним еще три:

Теперь пересчитаем – получилось 8.

Зря смеётесь! Когда считаем палочками – в Википедии это называется (ВНИМАНИЕ! НЕНОРМОТИВНАЯ ЛЕКСИКА!) «Единичная непозиционная система счисления с единичным весовым коэффициентом». Ну, или попросту будем называть УНАРНАЯ СИСТЕМА СЧИСЛЕНИЯ (1-СС).

В обычной жизни мы (люди) пользуемся ДЕСЯТЕРИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ (10-СС). Она так называется, потому что у нас есть десять цифр. К тому же, она еще и ПОЗИЦИОННАЯ, что означает, что значение (вес) цифры зависит от её положения в записи числа, например, в числах 2, 21 и 211 цифра 2 означает, соответственно, единицы, десятки и сотни.

Десятичная система счисления

Как мы складываем в 10-СС? Например, столбиком:

Сначала складываем единицы: 2+9 = 11, т.е. при сложении двух единичных чиселок появился новый десяток. Ясное дело, что из них может появиться только один десяток, потому что самое большое, что можно сложить – это 9+9 = 18. Таким образом, разбиваем сложение на кусочки: вместо 12+99 мы делаем 2+9 + 10+90, т.е. единицы и десятки (а потом и сотни) складываем отдельно друг от друга:

12 + 99 = [разобьем на разряды]

= (2+9) + (10+90) = [сложим первые разряды]

= 11 + (10+90) = [снова разобьем на десятки и единицы]

= (1 + 10) + (10 + 90) = [снова перегруппируем, чтобы отделить десятки от единиц]

= 1 + (10 + 10 + 90) = [сложим десятки]

= 1 + (110) = [разобьем на сотни и десятки]

Ясно, что получится 111, но давайте остановимся и посмотрим на эту полученную форму записи:

Фишка в том, что любое число можно представить как сумму отдельно единиц, отдельно десятков, сотен и т.д., например:

564 = 500 + 60 + 4, 7031 = 7000 + 000 + 30 + 1

Особенность такой записи в том, что мы видим во всех разрядах одну значащую цифру (первую), все следующие за ней цифры – это нули. Запомните этот момент – это важно.

При этом вместо того, чтобы писать 1000, мы можем написать 10^3 (т.е. десять в третьей степени, что можно расшифровать как 10*10*10).

7000 = 7*1000 = 7 * 10^3

А всё число 7031 можно расписать так:

7031 = 7*10^3 + 0*10^2 + 3*10^1 + 1*10^0

Напомню, что любое число в нулевой степени даёт единицу, и 10^0 = 1, а любое число в первой степени даёт само себя 10^1 = 10. Еще напомню, что любое число умноженное на 0 даёт 0, т.е. 0*10^2 = 0.

Так вот, наша система счисления называется десятичной именно благодаря этой десятке, которую в степень возводим.

Краткое отступление. Дорогие мои! Не путайте числа и цифры! Путать цифры и числа – это как путать буквы и звуки. Цифра – это просто символ для записи чисел. А число – это абстрактная величина, обычно означающее количество чего-нибудь. Думаю, все поняли. 🙂

Двоичная система счисления

Теперь, поговорим о 2-СС. Её особенность в том, что в ней есть всего 2 символа для записи чисел: 0 и 1. Что интересно, при этом любое число, которое можно записать в 10-СС, так же можно записать и в 2-СС, и даже в 1-СС!

Двоичная система тоже позиционная и отличается от десятичной тем, что в ней вместо 10 в степень возводится двойка, например, число двоичное число 101101 можно прочитать так:

101101= 1*2^5 + 0*2^4 + 1*2^3 + 1*2^2 + 0*2^1 + 1*2^0

= 32 + 0 + 8 + 4 + 0 + 1 = 45 (это уже в десятичной системе)

Теперь давайте поскладываем в двоичной системе.

Начнём с простого: 0+0 = 0, 1+0 = 1, 0+1 = 1

Ничего удивительного, в 10-СС это точно так же выглядит.

Теперь посложнее: 1 + 1 = 10

А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.

Нет. Это не десять плюс один! Это два плюс один! В 10-СС это выглядит так: 2 + 1 = 3, а в 1-СС так: || + | = |||. Ясно –понятно?

Хм… сложновато? Давайте упростим! По той же схеме, что и 12 + 99. Не забываем, что всё это в двоичной системе!

11 + 1 = [разобьем на разряды]

= (10 + 1) + 1 = [перегруппируем]

= 10 + (1 + 1) = [О! “1+1” складывать умеем!]

= 10 + 10 = [ну, здесь просто сначала игнорируем нули, складываем 1+1 и потом приписываем 0 к результату]

Ну, сколько можно. Это не СТО. Если то же самое записать в 10-СС, то получим: 3 + 1 = 4. Т.е. это 100 в записи 2-СС – это ЧЕТЫРЕ.

Ну, и для закрепления материала сложим в 2-СС:

= (1000 + 100 + 00 + 1) + (1000 + 000 + 00 + 1)

= (1000 + 1000) + (100 + 000) + (00 + 00) + (1 + 1)

= (10000) + (100) + (00) + (10)

= (10000) + (100) + (00 + 10)

А по-русски: 13 + 9 = 22

Большое спасибо! Очень хорошо объяснили. Всё понял.

А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи. И дальше нет объяснения почему и как. Естественно дальше идут примеры сложнее, но т.к. этот простой непонятен. Дальше залазить в дебри

поделитесь, пожалуйста, еще постами по информатике если есть

А теперь слушайте домашнее задание: построить синхрофазотрон.

Теперь посложнее: 1 + 1 = 10
Ой! Почему десять.
А вот никакие не ДЕСЯТЬ! Это число ДВА. Просто в двоичной записи.

Я тебя разочарую, но это десять и есть.

Кстати цифровая схемотехника основана на двоичной системе счисления. На основных законах булевой алгебры. 1+1=1 1+0=1 1*1=1 1*1=0

На самом деле все еще проще.

Нейронные сети. Формулы обратного распространения

Представляем заключительную лекцию из курса по нейронным сетям от 3blue1brown. В этой лекции речь пойдет о формулах обратного распространения. Одной из важных тем, которая позволит разобраться с основными моментами дифференцирования сложных функций в контексте сетей.

Благодарим за создание выпуска:

Переводчика – Федора Труфанова;

Редактора – Михаила Коротеева;

Диктора – Никифора Стасова;

Монтажера – Олега Жданова

Нейронные сети. Обратное распространение ошибки

Привет, Лига образования!

Мы продолжаем переводить легендарный курс по нейросетям от 3blue1brown.

В предыдущей лекции мы узнали о градиентном спуске. Сегодня речь пойдет о методе обратного распространения — главном алгоритме обучения нейронных сетей.

Благодарим за создание выпуска:

Редактора – Михаила Коротеева;

Диктора – Никифора Стасова;

Монтажера – Олега Жданова

И бонус в комментариях, английский!

Нейронные сети. Градиентный спуск: как учатся нейронные сети

Обучение — сложный процесс не только для человека, но и для сущностей, порожденных разумом человека.

Мы подготовили долгожданное продолжение лекций по нейросетям. Градиентный спуск: как учатся нейронные сети.

Благодарим за участие в выпуске:

Редакторов – Дмитрия Титова, Михаила Коротеева, Дмитрия Мирошниченко;

Корректора – Дмитрия Мирошниченко;

Дикторов – Никифора Стасова, Дарью Яговкину;

Монтажера – Олега Жданова.

Разговор о системах счисления:
— Программист подарил своей женщине 5 роз, сказав «эта 101 роза тебе» (двоичная). Пещерный человек, подарил бы три розы, сказав «бери эти 111 роз» (унарная).
— То есть неандертальца от программиста отличает всего лишь ноль?
— Ну вообще введение 0 было огромным шагом для математики. Можно сказать первый мощный шаг к абстрактному мышлению. Так что в какой-то степени да, «0» — это переходная ступень между неандертальцем и программистом.

Нейронные сети. Просто о сложном

Привет, Пикабу. Сегодня у нас кое-что действительно классное для Лиги образования.

Мы договорились о переводе и озвучке с автором самых крутых на Youtube видео про математику-информатику-физику.

И наша первая озвучка — видео о том, что же такое нейросети.

За это отличную озвучку мы благодарим Александра Колдаева.

Если хочешь поучаствовать в переводе или озвучке — напиши нам в вк, телеграм или facebook.

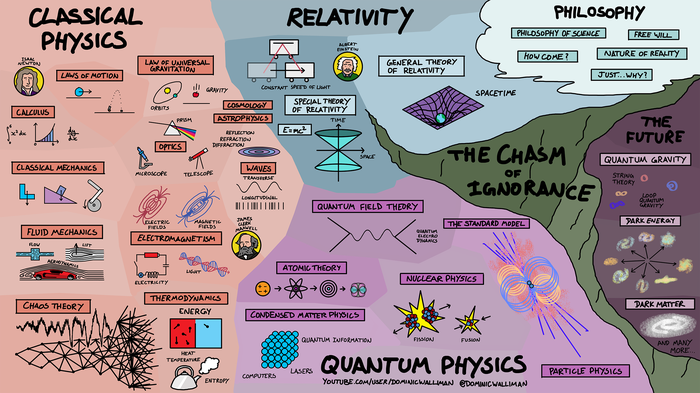
Карты наук

Выше был их автор. А вот и одна из его карт (по физике):

О карте, нарисованной выше, Dominic подробно рассказал в следующем видео. Он рассказал о ранней физике, об Эйнштейне и его теориях специальной и общей относительности, и о подвидах квантовой физики.

Кстати говоря, помимо карт наук, на его странице во flickr есть интересные постеры о том, как мы уже сейчас используем квантовые технологии.

Все его видео по картам наук публикуются в следующем плейлисте: https://www.youtube.com/playlist?list=PLOYRlicwLG3St5aEm02nc.
Они на английском, но уже есть и переводы.

Вот, например, по Computer Science:

А вот по математике:

Спасибо за внимание!

За день до экзамена

Ну, может и не сильно-то ждёт. Ну да ладно, всё равно любит. Наверное.

Источник

Степени двойки информатика 7 класс

Этот вспомогательный материал, который может быть полезен для подготовки к ГИА по информатике, в частности задач 15 ГИА, задач 1 ГИА, B10 ЕГЭ по информатике

Степени двойки таблица

2 0

1
2 1	2
2 2	4
2 3	8
2 4	16
2 5	32
2 6	64
2 7	128
2 8	256
2 9	512
2 10	1024
2 11	2048
2 12	4096
2 13	8192
2 14	16384
2 15	32768
2 16	65536
2 17	131072
2 18	262144
2 19	524288
2 20	1048576

Автор: Александр Чернышов

Оцените статью, это очень поможет развитию сайта.

Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.

Как пользоваться таблицей степеней числа два?

Степень двойки (n)	Значение степени двойки 2 n	Максимальное число без знака, записанное с помощью n бит
1	–	–
1	2	1	–
2	4	3	1
3	8	7	3
4	16	15	7
5	32	31	15
6	64	63	31
7	128	127	63
8	256	255	127
9	512	511	255
10	1 024	1 023	511
11	2 048	2 047	1023
12	40 96	4 095	2047
13	8 192	8 191	4095
14	16 384	16 383	8191
15	32 768	32 767	16383
16	65 536	65 535	32767
17	131 072	131 071	65 535
18	262 144	262 143	131 071
19	524 288	524 287	262 143
20	1 048 576	1 048 575	524 287
21	2 097 152	2 097 151	1 048 575
22	4 194 304	4 194 303	2 097 151
23	8 388 608	8 388 607	4 194 303
24	16 777 216	16 777 215	8 388 607
25	33 554 432	33 554 431	16 777 215
26	67 108 864	67 108 863	33 554 431
27	134 217 728	134 217 727	67 108 863
28	268 435 456	268 435 455	134 217 727
29	536 870 912	536 870 911	268 435 455
30	1 073 741 824	1 073 741 823	536 870 911
31	2 147 483 648	2 147 483 647	1 073 741 823
32	4 294 967 296	4 294 967 295	2 147 483 647

Примеры использования таблицы степеней числа два

Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.

Аналогично, 2 в 11 степени равно 2048.
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072

Таблица степеней чисел с 1 до 10. Калькулятор степеней онлайн. Интерактивная таблица и изображения таблицы степеней в высоком качестве.

Калькулятор степеней

С помощью данного калькулятора вы сможете в режиме онлайн вычислить степень любого натурального числа. Введите число, степень и нажмите кнопку «вычислить».

Таблица степеней от 1 до 10

n	1	2	3	4	5	6	7	8	9	10
1 n	1	1	1	1	1	1	1	1	1	1
2 n	2	4	8	16	32	64	128	256	512	1024
3 n	3	9	27	81	243	729	2187	6561	19683	59049
4 n	4	16	64	256	1024	4096	16384	65536	262144	1048576
5 n	5	25	125	625	3125	15625	78125	390625	1953125	9765625
6 n	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7 n	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8 n	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9 n	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10 n	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

Таблица степеней от 1 до 10

10 10 = 10000000000

Теория

Степень числа – это сокращенная запись операции многократного умножения числа самого на себя. Само число в данном случае называется – основанием степени, а количество операций умножения – показателем степени.

запись читается: «a» в степени «n».

«a» – основание степени

«n» – показатель степени

4 6 = 4 × 4 × 4 × 4 × 4 × 4 = 4096

Данное выражение читается: 4 в степени 6 или шестая степень числа четыре или возвести число четыре в шестую степень.

Источник

Таблица степеней 2 (двойки) от 0 до 32

Ниже представлена таблица степеней числа 2. Она даст нам представление необходимого числа бит, которое нам необходимо для хранения чисел.

Как пользоваться таблицей степеней числа два?

Степень двойки (n)	Значение степени двойки 2 n	Максимальное число без знака, записанное с помощью n бит
0	1	—	—
1	2	1	—
2	4	3	1
3	8	7	3
4	16	15	7
5	32	31	15
6	64	63	31
7	128	127	63
8	256	255	127
9	512	511	255
10	1 024	1 023	511
11	2 048	2 047	1023
12	40 96	4 095	2047
13	8 192	8 191	4095
14	16 384	16 383	8191
15	32 768	32 767	16383
16	65 536	65 535	32767
17	131 072	131 071	65 535
18	262 144	262 143	131 071
19	524 288	524 287	262 143
20	1 048 576	1 048 575	524 287
21	2 097 152	2 097 151	1 048 575
22	4 194 304	4 194 303	2 097 151
23	8 388 608	8 388 607	4 194 303
24	16 777 216	16 777 215	8 388 607
25	33 554 432	33 554 431	16 777 215
26	67 108 864	67 108 863	33 554 431
27	134 217 728	134 217 727	67 108 863
28	268 435 456	268 435 455	134 217 727
29	536 870 912	536 870 911	268 435 455
30	1 073 741 824	1 073 741 823	536 870 911
31	2 147 483 648	2 147 483 647	1 073 741 823
32	4 294 967 296	4 294 967 295	2 147 483 647

Примеры использования таблицы степеней числа два

Например, нам необходимо узнать, в какую степень нужно возвести число 2, чтобы получить 256. Во втором столбце находим число 256 и считываем, что 256 это два в степени восемь.

Аналогично, 2 в 11 степени равно 2048.
2 в 13 степени равно 8,192.
2 в 15 степени равно 32,768
2 в 17 степени равно 131,072

Источник