Что такое светящаяся точка в физике

Построение изображения в линзе

теория по физике 🧲 оптика

Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.

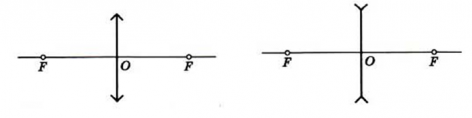
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.

Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.

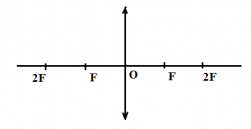
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.

Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.

Построение изображения в собирающей линзе

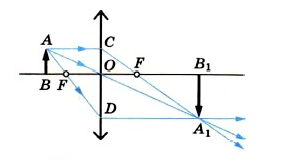
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:

Два вида лучей при построении изображений в линзе

Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).

Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.

На пересечении двух лучей обозначаем точку А₁. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В₁. Изображение предмета при этом — А₁ В_1.

В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.

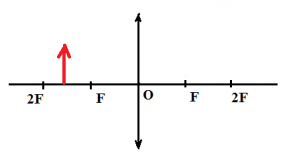
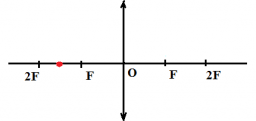
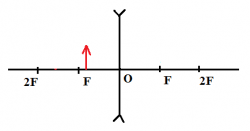
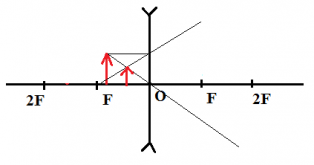
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.

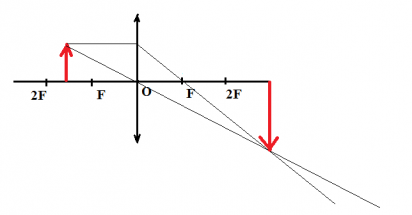
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.

Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.

Частный случай — построение изображения точки

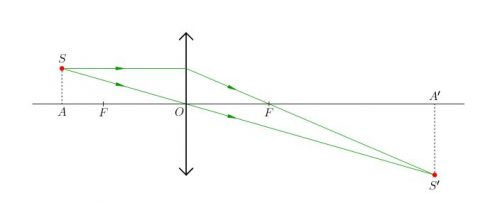
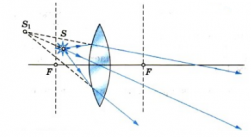
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.

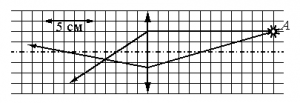
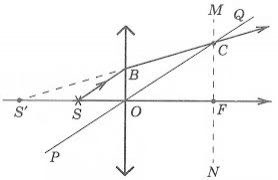
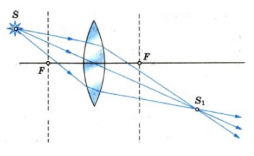
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.

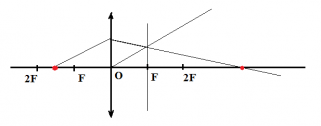
Пример №2. Построить изображение точки, расположенной на главной оптической оси.

Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.

Построение изображения в рассеивающей линзе

Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:

Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).

Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.

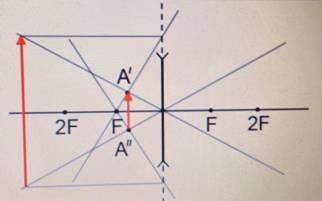
Пример №3. Построить изображение предмета в рассеивающей линзе.

Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.

Построение изображений в плоском зеркале

Плоское зеркало — это плоская поверхность, зеркально отражающая свет.

Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.

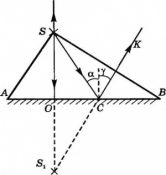
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S₁, которое представляет собой точку пересечения продолжения отраженных лучей.

Таким образом, чтобы получить изображение в плоском зеркале, нужно:

Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.

Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S₁OC равны по стороне и двум углам. Следовательно SO = S₁O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.

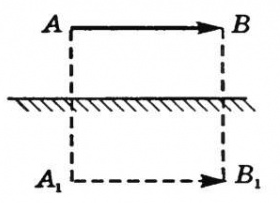
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А₁В₁ соответствует предмету АВ.

Изображение и сам предмет всегда симметричны относительно зеркала.

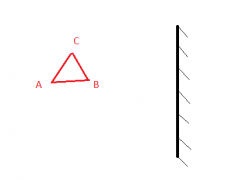
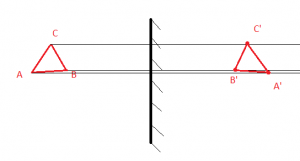
Пример №4. Построить изображение треугольника ABC в плоском зеркале.

Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.

Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.

Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.

Источник

Что такое светящаяся точка в физике

Свет – это электромагнитные волны, длины волн которых лежат для среднего глаза человека в пределах от 400 до 760 нм. В этих пределах свет называется видимым. Свет с наибольшей длиной волны кажется нам красным, а с наименьшей – фиолетовым. Запомнить чередование цветов спектра легко с помощью поговорки «Каждый Охотник Желает Знать, Где Сидит Фазан». Первые буквы слов поговорки соответствуют первым буквам основных цветов спектра в порядке убывания длины волны (и соответственно возрастания частоты): «Красный – Оранжевый – Желтый – Зеленый – Голубой – Синий – Фиолетовый». Свет с большими, чем у красного, длинами волн, называется инфракрасным. Его наш глаз не замечает, но наша кожа фиксирует такие волны в виде теплового излучения. Свет с меньшими, чем у фиолетового, длинами волн, называется ультрафиолетовым.

Электромагнитные волны (и, в частности, световые волны, или просто свет) – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Световые волны, как и любые другие электромагнитные волны, распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:

где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10 –12 Ф/м, μ₀ = 1,25664·10 –6 Гн/м. Скорость света в вакууме (где ε = μ = 1) постоянна и равна с = 3∙10 8 м/с, она также может быть вычислена по формуле:

Скорость света в вакууме является одной из фундаментальных физических постоянных. Если свет распространяется в какой-либо среде, то скорость его распространения также выражается следующим соотношением:

где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

Кроме света существуют и другие виды электромагнитных волн. Далее они перечислены по уменьшению длины волны (и соответственно, по возрастанию частоты):

Интерференция

Интерференция – одно из ярких проявлений волновой природы света. Оно связано с перераспределением световой энергии в пространстве при наложении так называемых когерентных волн, то есть волн, имеющих одинаковые частоты и постоянную разность фаз. Интенсивность света в области перекрытия пучков имеет характер чередующихся светлых и темных полос, причем в максимумах интенсивность больше, а в минимумах меньше суммы интенсивностей пучков. При использовании белого света интерференционные полосы оказываются окрашенными в различные цвета спектра.

Для расчета интерференции используется понятие оптической длины пути. Пусть свет прошел расстояние L в среде с показанием преломления n. Тогда его оптическая длина пути рассчитывается по формуле:

Для интерференции необходимо наложение хотя бы двух лучей. Для них вычисляется оптическая разность хода (разность оптических длин) по следующей формуле:

Именно эта величина и определяет, что получится при интерференции: минимум или максимум. Запомните следующее: интерференционный максимум (светлая полоса) наблюдается в тех точках пространства, в которых выполняется следующее условие:

Разность фаз колебаний при этом составляет:

При m = 0 наблюдается максимум нулевого порядка, при m = ±1 максимум первого порядка и так далее. Интерференционный минимум (темная полоса) наблюдается при выполнении следующего условия:

Разность фаз колебаний при этом составляет:

При первом нечетном числе (единица) будет минимум первого порядка, при втором (тройка) минимум второго порядка и т.д. Минимума нулевого порядка не бывает.

Дифракция. Дифракционная решетка

Дифракцией света называется явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий, размеры которых сопоставимы с длиной волны света (огибание светом препятствий). Как показывает опыт, свет при определенных условиях может заходить в область геометрической тени (то есть быть там, где его быть не должно). Если на пути параллельного светового пучка расположено круглое препятствие (круглый диск, шарик или круглое отверстие в непрозрачном экране), то на экране, расположенном на достаточно большом расстоянии от препятствия, появляется дифракционная картина – система чередующихся светлых и темных колец. Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Дифракционные решетки представляют собой периодические структуры, выгравированные специальной делительной машиной на поверхности стеклянной или металлической пластинки. У хороших решеток параллельные друг другу штрихи имеют длину порядка 10 см, а на каждый миллиметр приходится до 2000 штрихов. При этом общая длина решетки достигает 10–15 см. Изготовление таких решеток требует применения самых высоких технологий. На практике применяются также и более грубые решетки с 50–100 штрихами на миллиметр, нанесенными на поверхность прозрачной пленки.

При нормальном падении света на дифракционную решетку в некоторых направлениях (помимо того, в котором изначально падал свет) наблюдаются максимумы. Для того, чтобы наблюдался интерференционный максимум, должно выполняться следующее условие:

где: d – период (или постоянная) решетки (расстояние между соседними штрихами), m – целое число, которое называется порядком дифракционного максимума. В тех точках экрана, для которых это условие выполнено, располагаются так называемые главные максимумы дифракционной картины.

Законы геометрической оптики

Геометрическая оптика – это раздел физики, в котором не учитываются волновые свойства света. Основные законы геометрической оптики были известны задолго до установления физической природы света.

Закон прямолинейного распространения света: в оптически однородной среде свет распространяется прямолинейно. Этот закон приводит к представлению о световом луче как о геометрической линии, вдоль которой распространяется свет. Следует отметить, что закон прямолинейного распространения света нарушается и понятие светового луча утрачивает смысл, если свет проходит через малые отверстия, размеры которых сравнимы с длиной волны (в этом случае наблюдается дифракция).

На границе раздела двух прозрачных сред свет может частично отразиться так, что часть световой энергии будет распространяться после отражения по новому направлению, а частично пройти через границу и распространяться во второй среде.

Закон отражения света: падающий и отраженный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости (плоскость падения). Угол отражения γ равен углу падения α. Заметьте, что все углы в оптике измеряются от перпендикуляра к границе раздела двух сред.

Закон преломления света (закон Снеллиуса): падающий и преломленный лучи, а также перпендикуляр к границе раздела двух сред, восстановленный в точке падения луча, лежат в одной плоскости. Отношение синуса угла падения α к синусу угла преломления β есть величина, постоянная для двух данных сред, и определяется выражением:

Закон преломления был экспериментально установлен голландским ученым В.Снеллиусом в 1621 году. Постоянную величину n₂₁ называют относительным показателем преломления второй среды относительно первой. Показатель преломления среды относительно вакуума называют абсолютным показателем преломления.

Среду с большим значением абсолютного показателя называют оптически более плотной, а с меньшим – менее плотной. При переходе из менее плотной среды в более плотную луч «прижимается» к перпендикуляру, а при переходе из более плотной в менее плотную – «удаляется» от перпендикуляра. Единственный случай, когда луч не преломляется, это если угол падения равен 0 (то есть лучи перпендикулярны границе раздела сред).

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

ЗАПРЕЩЕНО использование представленных на сайте материалов или их частей в любых коммерческих целях, а также их копирование, перепечатка, повторная публикация или воспроизведение в любой форме. Нарушение прав правообладателей преследуется по закону. Подробнее.

Источник

Линза. Виды линз. Фокусное расстояние.

теория по физике 🧲 оптика

Мы уже познакомились с явлением преломления света на границе двух плоских сред. Но на практике особый интерес представляет явление преломления света на сферических поверхностях линз.

Линза — прозрачное тело, ограниченное сферическими поверхностями.

Какими бывают линзы?

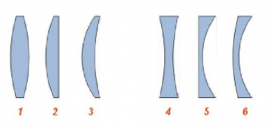
По форме различают следующие виды линз:

Выпуклые линзы тоже имеют разновидности:

Разновидности вогнутых линз:

Тонкая линза

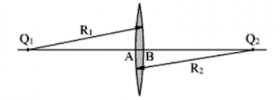
Мы будем говорить о линзах, у которых толщина l = AB намного меньше радиусов сферических поверхностей этой линзы R₁ и R₂. Такие линзы называют тонкими.

Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами сферических поверхностей, которыми она ограничена.

Главная оптическая ось тонкой — прямая, проходящая через центры сферических поверхностей линзы (на рисунке она соответствует прямой O₁O₂).

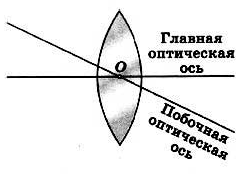
Оптический центр линзы — точка, расположенная в центре линзы на ее главной оптической оси (на рисунке ей соответствует точка О). При прохождении через оптический центр линзы лучи света не преломляются.

Побочная оптическая ось — любая другая прямая, проходящая через оптический центр линзы.

Изображение в линзе

Подобно плоскому зеркалу, линза создает изображения источников света. Это значит, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в точку (изображение) независимо от того, какую часть линзы прошли лучи.

Оптическое изображение — картина, получаемая в результате действия оптической системы на лучи, испускаемые объектом, и воспроизводящая контуры и детали объекта.

Практическое использование изображений часто связано с изменением масштаба изображений предметов и их проектированием на поверхность (киноэкран, фотоплёнку, фотокатод и т. д.). Основой зрительного восприятия предмета является его изображение, спроектированное на сетчатку глаза.

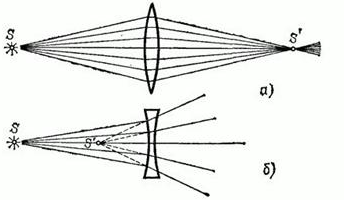
Изображения разделяют на действительные и мнимые. Действительные изображения создаются сходящимися пучками лучей в точках их пересечения (см. рисунок а). Поместив в плоскости пересечения лучей экран или фотоплёнку, можно наблюдать на них действительное изображение.

Если лучи, выходящие из оптической системы, расходятся, но если их мысленно продолжить в противоположную сторону, они пересекутся в одной точке (см. рисунок б). Эту точку называют мнимым изображением точки-объекта. Она не соответствует пересечению реальных лучей, поэтому мнимое изображение невозможно получить на экране или зафиксировать на фотоплёнке. Однако мнимое изображение способно играть роль объекта по отношению к другой оптической системе (например, глазу или собирающей линзе), которая преобразует его в действительное.

Собирающая линза

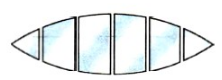
Обычно линзы изготавливают из стекла. Все выпуклые линзы являются собирающими, поскольку они собирают лучи в одной точке. Любую из таких линз условно можно принять за совокупность стеклянных призм. В воздухе каждая призма отклоняет лучи к основанию. Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.

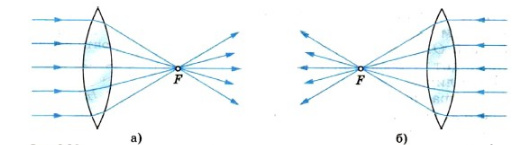
Если на линзу падают световые лучи, параллельные главной оптической оси, то при прохождении через нее они собираются на одной точке, лежащей на оптической оси. Ее называют главным фокусом линзы. У выпуклой линзы их два — второй главный фокус находится с противоположной стороны линзы. В нем будут собираться лучи, которые будут падать с обратной стороны линзы.

Главный фокус линзы обозначают буквой F.

Фокусное расстояние — расстояние от главного фокуса линзы до их оптического центра. Оно обозначается такой же букой F и измеряется в метрах (м).

В однородных средах главные фокусы собирающих линз находятся на одинаковом расстоянии от оптического центра.

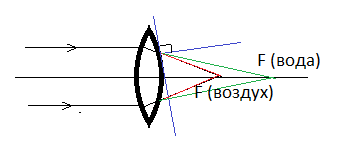
Пример №1. Что произойдет с фокусным расстоянием линзы, если ее поместить в воду?

Вода — оптически более плотная среда, поэтому преломленные лучи будут располагаться ближе к перпендикуляру, восстановленному к разделу двух сред. Следовательно, фокусное расстояние увеличится. На рисунке лучам, выходящим из линзы в воздухе, соответствуют красные линии. Лучам, выходящим из линзы в воде — зеленые. Видно, что зеленые линии больше приближены к перпендикуляру, восстановленному к разделу двух сред, что соответствует закону преломления света.

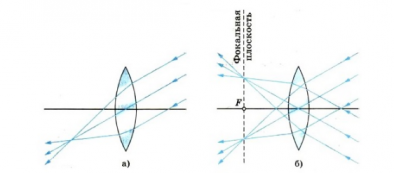
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси собирающей линзы. Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке (рисунок а). Но точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, будут располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус (рисунок б). Эту плоскость называют фокальной плоскостью.

Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.

Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.

Когда же источник света находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.

Рассеивающая линза

Вогнутые линзы обычно являются рассеивающими (лучи, выходя из них, не собираются, а рассеиваются). Это бывает если, поместить вогнутую линзу в оптически менее плотную среду по сравнению с материалом, из которого изготовлена линза. Так, стеклянная линза в воздухе является рассеивающей.

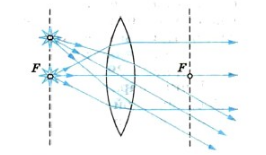
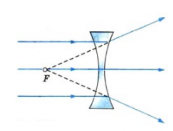
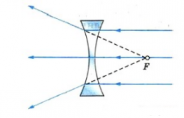
Если направить на вогнутую линзы световые лучи, являющиеся параллельными главной оптической оси, то образуется расходящийся пучок лучей. Если провести их продолжения, то они пересекутся в главном фокусе линзы. В этом случае фокус (и изображение в нем) является мнимым. Этот фокус располагается на фокусном расстоянии, равном F.

Другой мнимый фокус находится по другую сторону линзы на таком же расстоянии при условии, что среда по обе стороны линзы одинаковая.

Оптическая сила линзы

Оптическая сила линзы — величина, характеризующая преломляющую способность симметричных относительно оси линз и центрированных оптических систем, состоящих из таких линз.

Обозначается оптическая сила линзы буквой D. Единица измерения — диоптрий (дптр). Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.

Оптическая сила линзы равна величине, обратной ее фокусному расстоянию:

На рисунке показан ход двух лучей от точечного источника света А через тонкую линзу. Какова приблизительно оптическая сила этой линзы?

Источник