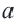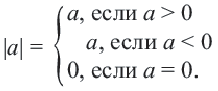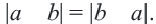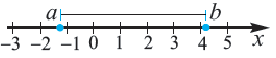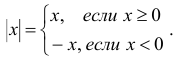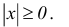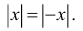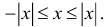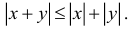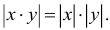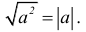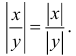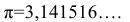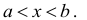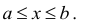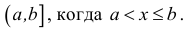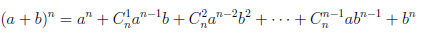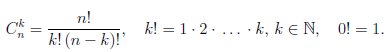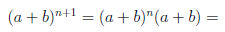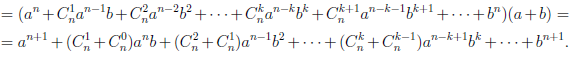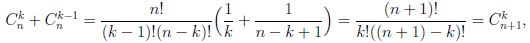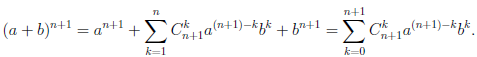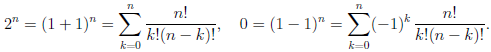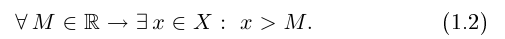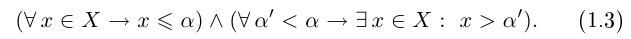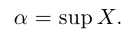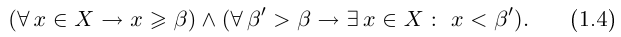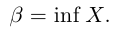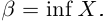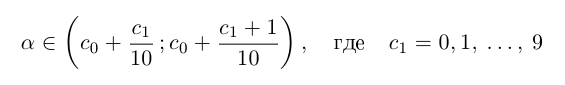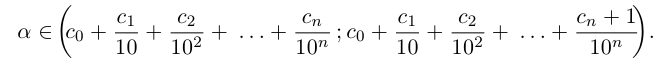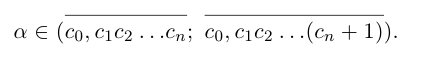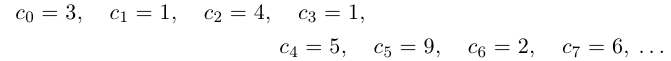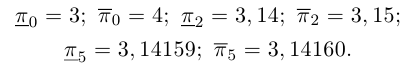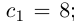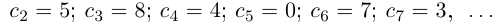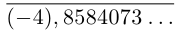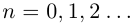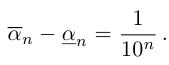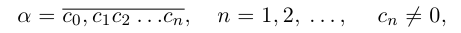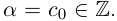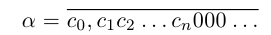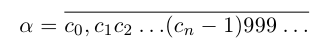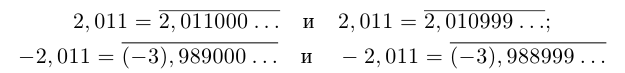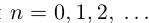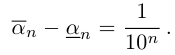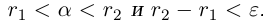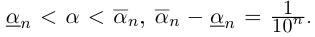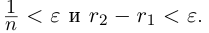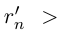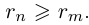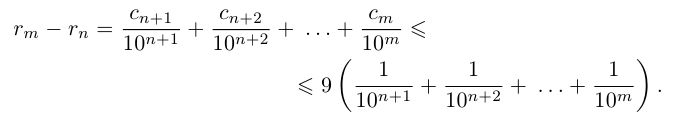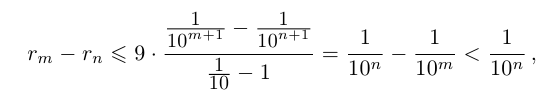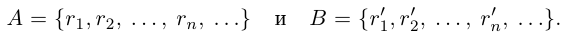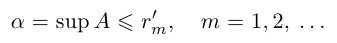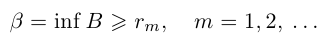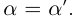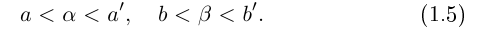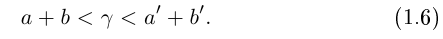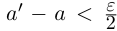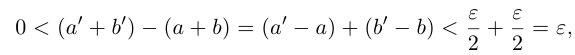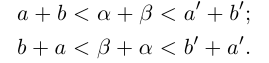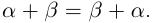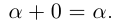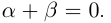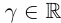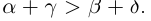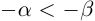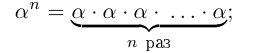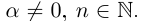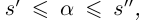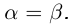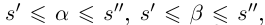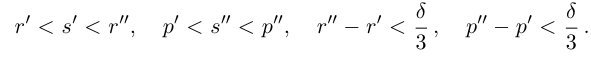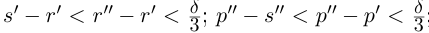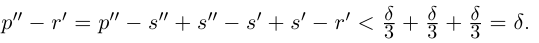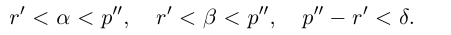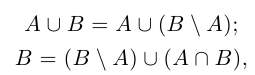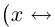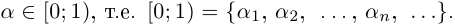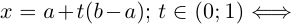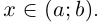Что такое вещественные числа
Содержание:
Действительные числа
В основе применения математических методов при решении практических задач лежат вычисления и измерения. При счете используются натуральные числа. При делении целого на части натуральных чисел недостаточно. Поэтому вводятся дробные числа. Длину отрезка можно выразить с помощью рационального числа с любой точностью. В теоретических вычислениях приходится рассматривать отрезки, длины которых не выражаются с помощью рациональных чисел. По этой причине вводится понятие иррационального числа. Изменение значений величины в противоположном направлении удобнее показать отрицательными числами.
Действительные числа
Рациональные и иррациональные числа образуют множество действительных чисел. Любое действительное число можно представить в виде бесконечной десятичной дроби. Для любого действительного числа
Для любых действительных чисел 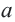
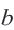
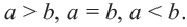
Абсолютная величина действительного числа показывает расстояние на числовой оси от точки, соответствующей этому числу, до начала отсчета.
Расстояние между двумя точками числовой оси равно абсолютной величине разности их координат 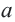
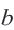

Действительные (вещественные числа)
Комплексные числа. Однако не успело ещё закрепиться новое расширенное понятие числа, как в процессе развития математики обнаружилось, что и новое понятие является также неудовлетворительным. В частности, решение квадратных уравнений уже на самой ранней ступени развития алгебры привело в области действительных чисел операции извлечения корня из отрицательного числа. Выяснилось, что среди действительных чисел нет ни одного такого, квадрат которого был бы величиной отрицательной, следовательно, и корень
квадратный из отрицательной величины 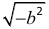
Абсолютная величина действительного числа
Абсолютной величиной (или модулем) действительного числа х (обозначается |х|) называется неотрицательное действительное число,
удовлетворяющее условиям:
Свойства абсолютных величин:
1.
2.
3.
4. Пусть 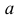
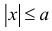
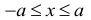
5. Для любых двух действительных чисел справедливы неравенства
6. Для любых двух действительных чисел справедливы неравенства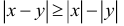
7.
8.
9.
Постоянные и переменные величины
Постоянной величиной называется величина, численные значения которой не меняются.
Величина с одним и тем же названием может быть постоянной (скорость равномерного движения) или переменной (скорость равномерно ускоренного движения).
Величины, которые сохраняют своё значение в любом явлении, называются абсолютными постоянными, например число
Переменной величиной называется величина, которая принимает различные числовые значения.
Совокупность всех числовых значений переменной величины называется областью изменения этой величины.
Промежутком или открытым интервалом (а,b) называется совокупность всех чисел х, заключенных между данными числами 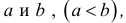
Отрезком или закрытым интервалом 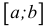
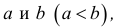
Естественным образом определяются полуоткрытые интервалы, т.е. промежутки, открытые с одной стороны. Например: 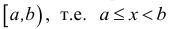
Определения интервалов можно сформулировать, используя вместо понятия «число» понятие «точка».
Окрестностью данной точки 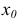
Действительные числа
Число является одной из основных математических абстракций, изучению которой может быть посвящен самостоятельный курс. Из многих концепций построения множества действительных чисел приведем аксиоматическую.
Определение 1.17. Множество R называется множеством вещественных чисел, а его элементы — вещественными (действительными) числами, если выполнен следующий комплекс условий, называемый аксиоматикой вещественных чисел:
1. Аксиомы сложения
(a) x + y = y + x, ∀x, y ∈ 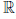
(b) в 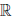
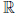
(c) для любого элемента x ∈ 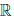
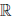
(d) x + (y + z) = (x + y) + z, ∀x, y, z ∈ 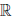
2. Аксиомы умножения
(a) x ∙ y = y ∙ x, ∀x,y ∈ 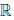
(b) в 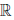
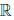
(c) для любого элемента x ∈ 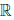
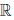
(d) x ∙ (y ∙ z) = (x ∙ y) ∙ z, ∀x,y,z ∈ 
(e) (x + y) ∙ z = x ∙ z + y ∙ z, ∀x,y., z ∈ 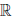
Множество, на котором определены обе операции, и которые удовлетворяют группам аксиом 1 и 2, называется алгебраическим полем.
(Часто знак операции умножения в математических выражениях опускают и вместо x ∙ y пишут xy.)
3. Аксиомы порядка
Для любых элементов x, y ∈ 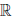



(a) x 

(b) если x, y ∈ 


(c) если x, y, z ∈ 



(d) если x, y, z ∈ 


(e) если x,y ∈ 


Отношение 


4. Аксиома полноты (непрерывности)
Если X и Y — непустые подмножества множества 

x 

Эту аксиому часто называют принципом отделимости.
Можно доказать, что во введенном множестве R имеют место все, известные из школьного курса математики, свойства чисел. Желающие могут получить их самостоятельно или изучить соответствующий раздел в книгах [2] или [6].
Важнейшие подмножества действительных чисел
Определение 1.18. Множество X ⊂ 
Множество натуральных чисел обозначают через 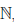
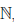
0 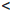
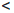
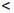
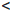
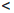
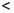
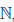
Прямым следствием определения 1.18 является принцип математической индукции.
Если подмножество E множества натуральных чисел 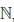
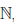
Иллюстрируя этот принцип в действии, докажем с его помощью формулу, называемую формулой бинома Ньютона:
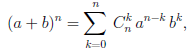
В этой формуле a, b — произвольные действительные числа, n — произвольное натуральное число,
Пусть E — множество тех натуральных чисел n, для которых справедлива формула (1.1). При 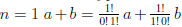
Но 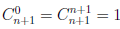
Таким образом, n + 1 ∈ E и, следовательно, E = 
Определение 1.19. Множество, состоящее из всех натуральных чисел, им противоположных и нуля называют множеством целых чисел и обозначают символом Z.
Определение 1.20. Множество 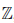
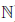
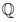
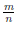
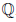
Можно доказать, что 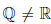
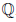
Определение 1.21. Действительные числа, которые не являются рациональными, называются иррациональными.
Часто полезна «геометрическая терминология в которой множество 
Пусть a, b ∈ 
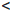

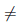
[a, b] := 

(a, b) := 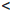
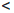
(a, b] := 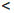

[a, b) := 
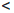
В этих обозначениях часто пишут: 
Действительные числа
Определение действительного числа по Дедекинду
Одним из основных понятий, изучаемых в курсе математического анализа, является понятие действительного числа. Оно возникает в школьном курсе элементарной алгебры фактически на интуитивном уровне как развитие понятия о числе — от натуральных чисел к целым, от целых к рациональным, от рациональных к действительным. В нашу задачу не входит сейчас аккуратное выведение этой цепочки из основных представлений о натуральных числах и их свойствах. Будем считать, что понятие рационального числа и основные свойства рациональных чисел, а также другие вопросы школьного курса элементарной алгебры (в частности, основная символика теории множеств) хорошо известны. Напомним, что множество натуральных чисел обозначается N, множество целых чисел — Z. множество рациональных чисел — Q.
При переходе к действительным числам (множество которых обозначается R) возникает качественно новое понятие непрерывности, присущее именно математическому анализу Поэтому этот шаг будет разобран подробно и аккуратно.
Определение 1.1. Сечением а множества рациональных чисел Q называется такое разбиение Q на два непустых множества 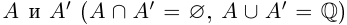
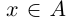
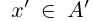
Легко видеть, что в примере 1) в нижнем классе А есть наибольший элемент в верхнем классе А’ нет наименьшего элемента. В примере 2) в A нет наибольшего элемента, в А’ есть наименьший. В примере 3) в A нет наибольшего элемента, в А’ нет наименьшего.
Докажем, например, что в примере 3) в A нет наибольшего элемента (значком □ будем обозначать начало доказательства, значком ■ — конец доказательства).
□ Доказательство от противного. Пусть в А есть наибольший элемент г. Тогда г > 0, г 2 2 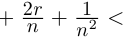
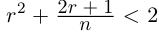
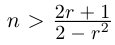
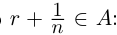
Докажем теперь, что невозможен случай, когда в А есть наибольший элемент, в А’ есть наименьший.
□ Пусть существуют 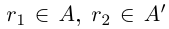
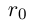
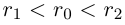
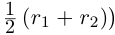
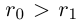
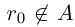
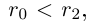
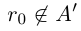
Итак, существуют сечения трёх типов.
I. В нижнем классе есть наибольший элемент, в верхнем нет наименьшего.
II. В нижнем классе нет наибольшего элемента, в верхнем есть наименьший.
III. В нижнем классе нет наибольшего элемента, в верхнем нет наименьшего.
Определение 1.2. Иррациональным числом называется сечением III типа.
В случаях I и II говорят, что сечение производится рациональным числом (соответствующим наибольшему элементу в нижнем классе или наименьшему в верхнем). Сечения I и II типов отождествляются с соответствующими рациональными числами. Чтобы соответствие было взаимно однозначным, сечения типа I в дальнейшем не рассматриваются.
Например, сечение в примере 1) мы не будем рассматривать. Сечение в примере 2) — это рациональное число 1. Сечение в примере 3) — это иррациональное число (которое естественно объявить корнем квадратным из 2, не придавая пока этому термину строгого смысла).
Определение 1.3. Действительным (вещественным) числом называется любое сечение II или III типов. Множество действительных чисел обозначается R. Сечения II типа отождествляются с соответствующими рациональными числами.
У сечений, соответствующих действительным числам, в нижнем классе нет наибольшего элемента. Если в верхнем классе есть наименьший элемент — сечение является рациональным числом, если нет — иррациональным.
Определение 1.4. Два действительных числа 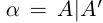
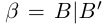
Определение 1.5. Рассмотрим два неравных действительных числа 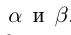
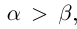
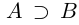
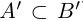
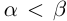
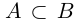
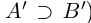
Символ > читается «больше», символ М.
Запишем окончательно на языке кванторов, что означает неограниченность множества X сверху:
Наблюдая преобразование (1.1) в (1.2), мы можем сформулировать формальное правило построения отрицаний в позитивном смысле:
1) кванторы меняются друг на друга, т.е. 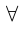
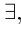
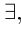
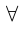
2)высказывания, стоящие при кванторах, не меняются;
3)существенные высказывания, не стоящие при кванторах, меняются на противоположные.
Пример 1.2. Множество N натуральных чисел ограничено снизу 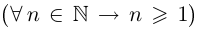
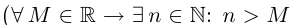
Определение 1.8. Действительное число л называется точной верхней гранью множества 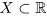
На языке кванторов это описывается как конъюнкция (т.е. одновременное выполнение) двух высказываний:
Логический символ 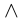
Точная верхняя грань обозначается sup («supremum»):
Определение 1.9. Действительное число 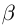
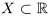
На языке кванторов записывается конъюнкция двух высказываний:
Точная нижняя грань обозначается inf («infimum»):
Из определений следует, что sup X — это наименьшая из верхних границ множества X, a inf X — это наибольшая из нижних границ. Пока ниоткуда не следует, что эти наименьшая из верхних и наибольшая из нижних границ существуют. Дело в том, что ограниченное сверху множество может иметь наибольший элемент, а может и не иметь; ограниченное снизу множество может иметь наименьший элемент, а может и не иметь.
Лемма 1.2. Если множество 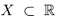
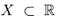
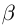
□ Доказательство приведём для наибольшего элемента, вторая часть доказывается аналогично.
Так как а — наибольший элемент X, то для всех 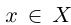
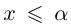
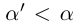
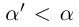
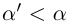
Но может быть и так, что во множестве нет наибольшего (наименьшего) элемента, а точная верхняя (нижняя) грань существует. В этом случае говорят, что точная верхняя (нижняя) грань не достигается.
Пример 1.3. Пусть 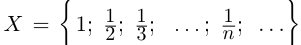
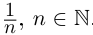
С другой стороны, ясно, что при всех 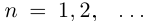
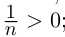
□ В самом деле, для всех 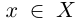
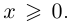
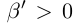
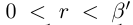
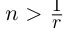
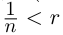
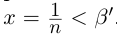
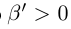
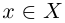
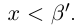
Теорема 1.5 (о точной верхней (нижней) грани). Для любого непустого множества действительных чисел, ограниченного сверху, существует и единственна точная верхняя грань. Для любого непустого множества действительных чисел, ограниченного снизу, существует и единственна точная нижняя грань.
□ Доказательство проведём для точной верхней грани, вторая часть доказывается аналогично (отметим, что пустое множество формально является ограниченным сверху и снизу, но говорить о точных верхней и нижней гранях бессмысленно).
Пусть сначала ограниченное сверху множество 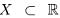
Пусть теперь в X нет наибольшего элемента. Проведём сечение во множестве К так, что А’ — это все верхние границы X (они существуют в силу ограниченности X сверху), а 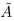
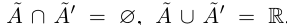
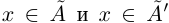
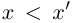
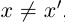
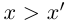
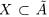
По теореме Дедекинда существует действительное число a либо наибольшее в 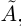
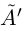
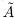
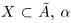
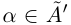
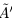
Докажем теперь, что точная верхняя грань единственна. Пусть a = supX и 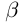
Определение 1.10. Если множество 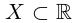
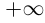
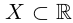
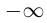
Представление действительных чисел бесконечными десятичными дробями
Пусть действительное число а не является целым числом или конечной десятичной дробью. Рассмотрим соответствующее сечение во множестве рациональных чисел 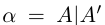
Обозначим через со наибольшее целое число в А. Тогда 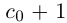
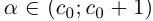
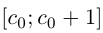
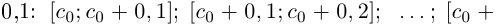
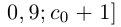
(a не совпадает с концом отрезка, так как не является конечной десятичной дробью).
Снова разбиваем полученный отрезок на 10 отрезков равной длины 0,01 и т.д., на n-м шагу получим
Естественно, что если сn = 9, то при переходе к правому концу отрезка предыдущую цифру 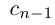

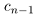
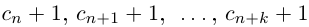
Так как а не является конечной десятичной дробью, то процесс никогда не оборвётся, и мы получим бесконечную последовательность цифр 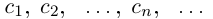
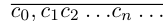
Например, для числа 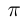
Описанная выше конструкция даст следующие интервалы:
Левый конец соответствующего интервала длины 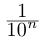
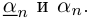
Бесконечная десятичная дробь 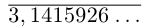
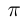
Интересно отмстить, что в такой конструкции для числа 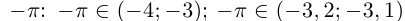
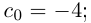
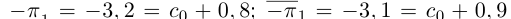
Представлением числа 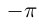
Легко видеть, что для любого
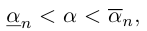
Особое значение имеет случай, когда а — конечная десятичная дробь с n знаками после запятой:
или целое число:
Случай целого a можно рассматривать как частный случай конечной десятичной дроби при n = 0.
В описанной выше конструкции после n-го шага процесс оборвётся. Число ft будет являться общим концом двух отрезков длины 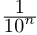
(для иллюстрации общности процесса мы дополнили её бесконечной последовательностью нулей). Если же a рассматривать как правый конец левого из двух возникших отрезков, то а представляется как бесконечная дробь, в которой начиная с (n + 1)-го места после запятой идут девятки:
Таким образом, конечная десятичная дробь имеет два десятичных представления (с нулями, начиная с некоторого места, и с девятками, начиная с некоторого места). Например:
В любом случае при
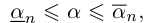
Докажем теперь очень важную лемму, которая неоднократно будет использоваться в дальнейшем в теории действительных чисел.
Лемма 1.4. Пусть a —действительное число. Тогда для любого рационального положительного числа s найдутся paциональные числа 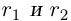
Иными словами, любое действительное число может быть зажато между двумя сколь угодно близкими рациональными числами.
□ Если a — рациональное число, то возьмём 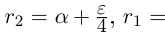
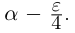
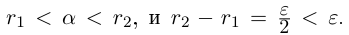
Поэтому можно взять 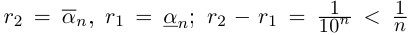
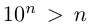
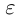
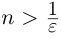
Мы видели, что любое действительное число представляется бесконечной десятичной дробью. Это представление единственно, если действительное число не является целым или конечной десятичной дробью, в противном случае таких представлений два. Докажем обратное утверждение.
Теорема 1.6. Любая бесконечная десятичная дробь является представлением некоторого действительного числа, причем это число определяется единственным образом.
□ Пусть 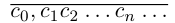

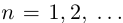
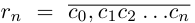
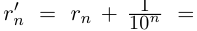

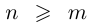
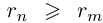
Пусть теперь 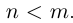
Применяя формулу суммы членов геометрической прогрессии, получим
поэтому 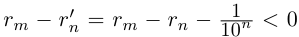
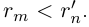
Рассмотрим множества рациональных чисел
При фиксированном 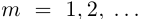
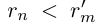
Аналогично, при фиксированном 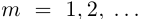
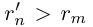
Из леммы 1.3 и последнего неравенства, верного при всех 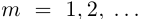
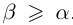
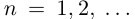
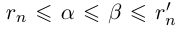
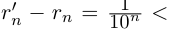
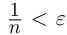
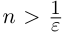
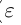
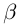
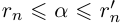
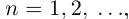
Единственность искомого действительного числа следует из леммы 1.1. В самом деле, если два числа 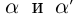
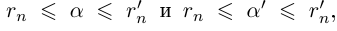
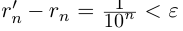
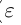
Арифметические операции с действительными числами
Нам предстоит определить для действительных чисел арифметические операции (сложение, вычитание, умножение, деление) так, чтобы сохранялись привычные свойства этих операций, а для рациональных чисел результаты операций не отличались от обычных.
Пусть 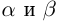
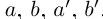
Определение 1.11. Суммой 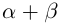
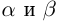
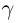
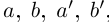
Докажем корректность этого определения. Иными словами, докажем, что такое действительное число 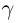
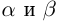
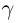
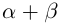
□ I) Существование. Рассмотрим множество всевозможных сумм <а + b>в условиях (1.5). Оно ограничено сверху некоторой суммой 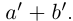
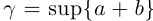
Тогда при выполнении условий (1.5) 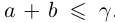
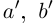
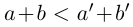
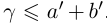
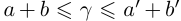
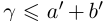
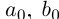
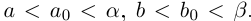
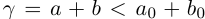
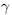
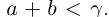
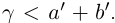
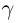
II) Единственность. По лемме 1.4 для любого положительного рационального числа 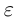
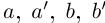
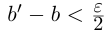
и эта разность может быть сделана сколь угодно малой. По лемме 1.1 существует единственное действительное число 7, удовлетворяющее условиям (1.6).
III) Преемственность. Если 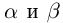
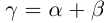
Теперь нужно показать, что привычные свойства операции сложения сохраняются для определённого таким образом сложения действительных чисел. Ввиду большого количества этих свойств будут проведены доказательства лишь некоторых из них; доказать остальные читатели смогут самостоятельно (наиболее существенные моменты будут показаны в доказательствах, приведённых здесь).
Свойства сложения действительных чисел
1) 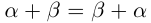
□ Рассмотрим рациональные числа 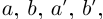
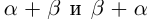
Так как сложение рациональных чисел коммутативно, то а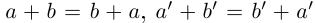
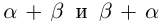
2) 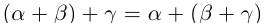
3)
4)Для любого действительного числа а найдётся число 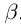
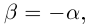
□ Если а — рациональное число, то 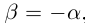
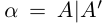
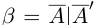
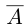
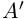
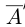
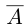
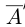
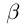
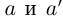
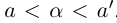
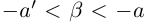
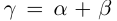
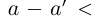
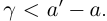
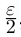
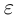
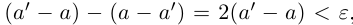
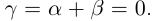
5)Если 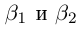
□ С одной стороны, 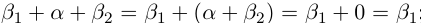
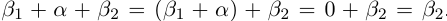
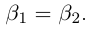
6)Если 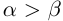

□ По лемме 1.2 найдутся рациональные числа 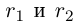
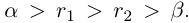
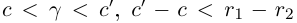
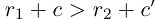
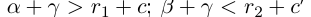
Значит, 
7)Если 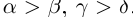
□ Двукратное применение предыдущего свойства. ■
8)Если 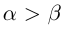
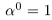
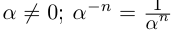
Сохраняются все свойства степеней с целым показателем (доказательства ничем не отличаются от доказательств в школьном курсе алгебры).
Обратим теперь внимание на то, что в лемме 1.1 действительное число зажималось между рациональными потому, что у нас ещё не было понятия разности действительных чисел. Приведём теперь более общий вариант этого утверждения.
Лемма 1.5. Пусть 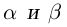
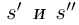
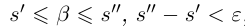
□ Пусть 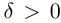
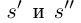
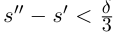
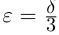
По лемме 1.4 найдутся рациональные числа 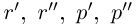
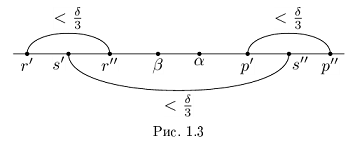
Тогда (см. рис. 1.3):
Итак, для любого рационального положительного числа 6 найдутся рациональные числа 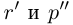
По лемме 1.1
Счётные и несчётные множества
Определение 1.16. Два множества А и В называются эквивалентными (равномощными), если между А и В можно установить взаимно однозначное (биективное) соответствие.
Здесь мы фактически имеем дело с переводом русскоязычного термина на латинский язык (равномощный — эквивалентный, взаимно однозначное — биективное и т.д.). В принципе вполне можно было бы ограничиться русскоязычными терминами, но, поскольку их переводы очень распространены в отечественной научной и учебной литературе, их игнорировать нельзя.
Пример 1.4. Множество натуральных чисел эквивалентно множеству чётных натуральных чисел (взаимно однозначное соответствие устанавливается зависимостью 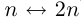
Определение 1.17. Множество называется счётным, если оно эквивалентно множеству натуральных чисел (т.е. если его элементы можно занумеровать в виде бесконечной последовательности).
Лемма 1.6. Любое бесконечное множество содержит счётное подмножество.
□ Выберем некоторый элемент х1, принадлежащий данному бесконечному множеству А. Так как множество бесконечно, то можно выбрать элемент х2 среди оставшихся элементов, х3 среди оставшихся и т.д. Процесс не оборвётся в силу бесконечности А. Построенное счётное множество 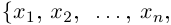
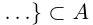
Лемма 1.7. Любое бесконечное подмножество счётного множества счётно.
□ Пусть 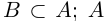
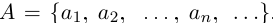
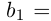
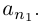
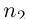
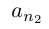
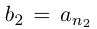
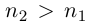
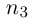
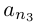
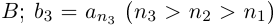
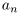
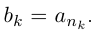
Лемма 1.8. Сумма конечного и счётного множеств, двух счётных множеств — счётна.
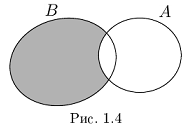
□ Напомним, что в теории множеств разностью множеств В \ А называется множество тех и только тех элементов, которые принадлежат В, но не принадлежат А (на диаграмме Эйлера заштрихована разность В \ А — см. рис. 1.4).
Из рис. 1.4 очевидны равенства
причём множества, объединяемые в правых частях этих равенств, имеют пустые пересечения.
1) Пусть А — счётно, В — конечно.
Если 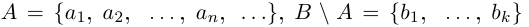
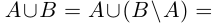
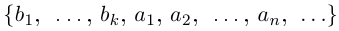
2) Пусть А и В счётны. Если В \ А конечно, то доказательство проходит, как в первом случае. Если В \ А бесконечно, т.е. счётно, то 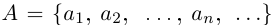
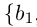
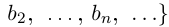
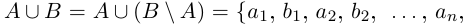
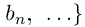
Теорема 1.7. Множество рациональных чисел Q счётно.
□ Достаточно доказать, что счётно множество положительных рациональных чисел Q+, так как в этом случае множество отрицательных рациональных чисел, эквивалентное ему 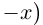
Занумерованы все положительные рациональные числа, причём каждое число встречается много раз 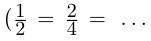
Следствие. Множество целых чисел Z счётно (принадлежит Q).
Теорема 1.8. Множество действительных чисел К несчётно (т.е. действительных чисел «значительно больше», чем рациональных).
□ Достаточно доказать, что несчётным является множество действительных чисел полуинтервала [0; 1) (если R — счётно, то [0; 1) 
Выпишем десятичные представления этих чисел:
при этом конечная десятичная дробь записывается с нулями, начиная с некоторого номера (а не с девятками).
Рассмотрим число 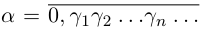
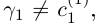

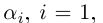
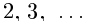
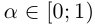
Следствие 1. Множество иррациональных чисел несчётно (иначе вместе с Q получилось бы счётное множество R).
Следствие 2. Множество чисел любого конечного интервала несчётно.
□ Множество (0; 1) несчётно, так как иначе при добавлении одной точки 0 получилось бы счётное множество [0; 1).
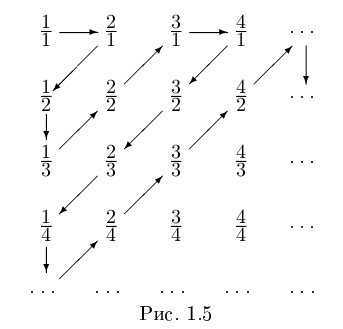
Несчётность произвольного интервала (а;b) следует из того, что между (0; 1) и (a: b) можно установить взаимно однозначное соответствие по формуле
Замечание к главе I. При помощи сечений были определены лишь арифметические операции с действительными числами. Развивая этот метод, можно определить арифметический корень n-й степени из положительного действительного числа, степень положительного числа с произвольным действительным показателем, логарифмы и другие элементарные функции, известные из школьного курса алгебры. Но если этим вопросам уделить внимание в лекционном курсе математического анализа, то возникнет нехватка времени для изложения последующих очень существенных глав.
Представляется удобным и разумным пойти путём наименьшего сопротивления — не вводить пока эти элементарные функции, ограничившись в главах II и III (теория пределов последовательностей и функций) арифметическими свойствами действительных чисел. И только в главе III, после изучения свойств непрерывных функций, ввести корень n-й степени как обратную функцию к х n на соответствующем промежутке, аккуратно определить степень с действительным показателем, логарифм как обратную функцию и т.д. Этот путь имеет один недостаток — обедняется практическая сторона курса, при решении иллюстрирующих примеров приходится ограничиваться арифметическими операциями. Конечно, на практических занятиях следует решать примеры с корнями, логарифмами, тригонометрическими функциями и т.д., но при этом понимать, что всё, выходящее за рамки арифметики, пока является «незаконным» и чисто иллюстративным.
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.