Что такое весовое значение позиции
Что такое вес позиции в системе счисления? Имеется десятичное число 324512. Какой вес имеет каждая позиция
В общую длину пути будет входить длина пути AC = 10
Длина пути напрямую из C в F (CF) = 8.
Нам нужно проверить, если ли смысл ехать в другой нас. пункт из C, чтоб сократить общий путь.
Варианты, где расстояние из C в другой нас. пункт больше или равно CF отбрасываем. У нас остаются:
Найдем общий размер пути, который нужно преодолеть с самого начала и найдем меньший
Ответ:
Длина кратчайшего пути между пунктами А и F, проходящая через пункт С = 15 (ACEF).
1)Первый жесткий диск это продукт, который разработала компания IBM в 1956 году, и вошел он в историю как начало компьютерной индустрии.
2)8,4 ГБ,128 ГБ
3)При операциях — чтения (read)
HDD медленее в 94 раза (0.68 МБ/с против 63.6 МБ/с), по сравнению с SSD
HDD медленее в 53 раза (0.36 МБ/с против 19 МБ/с), по сравнению с SSD
При операциях — записи (write)
HDD медленее в 178 раз (0.78 МБ/с против 139 МБ/с), по сравнению с SSD
HDD медленее в 86 раз (0.64 МБ/с против 55 МБ/с), по сравнению с SSD
4)В 1981 году стоимость 1 ГБ пространства на HDD составляла 500 000 долларов. Сейчас — 0,025 доллара.
5)Является основным накопителем данных в большинстве компьютеров.
Представление числовых значений
Несмотря на то, что метод хранения информации в виде закодированных символов достаточно удобен, он оказывается неэффективным при записи чисто числовой информации. Попробуем разобраться, почему это так. Предположим, что в память требуется записать число 25. Если воспользоваться символами в кодах ASCII, то для записи этого числа потребуется один байт на каждый символ, а всего — 16 бит. Более того, самое большое число, которое мы сможем представить с помощью 16 битов, — это 99. В данном случае эффективнее будет сохранить это число в его двоичном представлении.
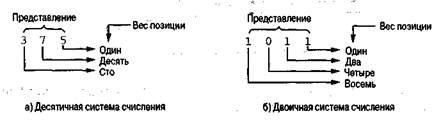
Двоичная система счисления представляет собой способ выражения цифровых величин с помощью только двух цифр (0 и 1), а не всех десяти (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), как в традиционной десятичной системе счисления. Напомним, что в десятичной системе счисления каждой цифровой позиции в представлении числа приписывается определенное весовое значение. Например, в представлении числа 375 позиция цифры 5 имеет весовое значение единица, позиция цифры 7 — весовое значение десять, а позиция цифры 3 — весовое значение сто (рис. 1.13, а). В этом случае весовое значение каждой позиции в десять раз пре-
восходит весовое значение следующей позиции. Представляемая величина определяется посредством умножения каждой цифры на весовое значение занимаемой ею позиции с последующим сложением полученных результатов. Таким образом, комбинация цифр 375 представляет величину (3 х сто) + (7 х десять) + (5 х один).
Для определения числового значения, представленного в двоичной системе счисления, выполняются те же действия, что и при записи его в десятичной системе счисления, — каждая его цифра умножается на весовое значение занимаемой ею позиции, и полученные результаты суммируются. На пример, двоичное число 100101 имеет значение 37, как показано на рис. 1.14. Более того, поскольку в двоичной системе счисления используются только цифры 0 и 1, общая процедура умножения и суммирования результатов сокращается до суммирования весовых значений позиций, в которых находятся единицы. Например, двоичное число, 1011 представляет значение 11 так как единицы в нем расположены в позициях с весовыми значениями один, два и восемь.
Рис 1.14 Расшифровка значения двоичного числа 100101
Представление изображений
Современные компьютерные приложения способны обрабатывать не только простейшие текстовые и цифровые данные. Помимо всего прочего, они позволяют работать с изображениями, а также с аудио- и видеоинформацией. В отличие от методов хранения символьной и числовой информации, способы представления данных в этих дополнительных форматах находятся еще на ранней стадии своего развития, а потому для них еще не существует общепризнанных стандартов.
Наиболее распространенные из существующих методов представления изображений можно разделить на две большие категории: растровые методы и векторные методы. При растровом методе изображение представляется как совокупность точек, называемых пикселями (pixel, сокращение от picture element — элемент изображения). Говоря упрощенно, изображение кодируется в виде длинных строк битов, которые представляют ряды пикселей в изображении. При этом каждый бит равен 0 или 1, в зависимости от того, является ли соответствующий пиксель черным или белым. Включение информации о цвете изображений лишь незначительно усложняет дело, поскольку в этом случае каждый пиксель представляется комбинацией битов, определяющей его цвет. При растровом методе полученную комбинацию битов часто называют битовой картой (bit map), подчеркивая тот факт, что данная комбинация битов представляет собой не более чем карту или схему исходного изображения.
Большинство периферийных устройств современных вычислительных машин, например факсимильные аппараты, видеокамеры или сканеры, преобразует цветные изображения в графические файлы с растровым форматом. Чаще всего эти устройства записывают цвет каждого пикселя, раскладывая его на три составляющие — красную, зеленую и синюю, соответствующие трем первичным цветам. Для передачи интенсивности каждой компоненты обычно используется один байт. Поэтому для представления каждого пикселя исходного изображения требуются три байта.
Аналогичный трехкомпонентный пиксельный подход к передаче графической информации используется и при выводе изображений на экраны мониторов современных компьютеров. Экраны этих устройств содержат десятки тысяч пикселей, каждый из которых состоит из трех компонентов (красного, зеленого и синего), что можно заметить даже невооруженным глазом, если внимательно посмотреть на экран. (Можно также воспользоваться увеличительным стеклом.)
Формат «три байта на пиксель» означает, что для хранения изображения, в котором 1280 рядов по 1024 пикселя (фотография обычного размера), потребуется несколько мегабайт памяти, что существенно превышает размер стандартной дискеты. Одним из недостатков растровых методов является трудность пропорционального изменения размеров изображения до произвольно выбранного значения. В сущности, единственный способ увеличить изображение — это увеличить сами пиксели. Однако это приводит к появлению зернистости, что также часто встречается и при фотографировании на пленку. Векторные методы позволяют избежать проблем масштабирования, характерных для растровых методов. В этом случае изображение представляется в виде совокупности линий и кривых. Вместо того чтобы заставлять устройство воспроизводить заданную конфигурацию пикселей, составляющих изображение, ему передается подробное описание того, как расположены образующие изображение линии и кривые. На основе этих данных устройство, в конечном счете, и создает готовое изображение. С помощью подобной технологии описываются различные шрифты, поддерживаемые современными принтерами и мониторами. Они позволяют изменять размер символов в широких пределах и по этой причине получили название масштабируемых шрифтов. Например, технология True Type, разработанная компаниями Microsoft и Apple Computer, описывает способ отображения символов в тексте. Для подобных целей предназначена и технология PostScript (разработанная компанией Adobe Systems), позволяющая описывать способ отображения символов, а также других, более общих графических данных. Векторные методы также широко применяются в автоматизированных системах проектирования (computer-aided design, CAD), которые отображают на экране мониторов чертежи сложных трехмерных объектов и предоставляют средства манипулирования ими. Однако векторная технология не позволяет достичь фотографического качества изображений объектов, как при использовании растровых методов. Именно поэтому в современных цифровых фотокамерах используются растровые методы представления изображения.
Двоичная система счисления
Что такое весовое значение позиции
Система счисления — это способ записи чисел.
Позиционная система счисления — это такая система, в которой вклад цифры зависит от её позиции в записи числа.
Вес позиции — это число, на которое умножается цифра, находящаяся в этой позиции.
Чтобы определить значение числа по его записи в позиционной системе счисления, нужно умножить цифры на веса их позиций и сложить результаты.
Основание позиционной системы счисления — это число, которое используется для определения веса позиций.
Вес первой позиции всегда равен единице. Вес каждой следующей позиции получается из веса предыдущей умножением на основание системы (нумерация справа налево).
Вариант 1
Прочитайте скороговорки, заменяя двоичные числа десятичными:
| Съел молодец 100001 2 пирога с пирогом, Да все с творогом. Шли 101000 2 мышей, |
Разгадайте двоично-буквенные ребусы:
| 1100100 Л | 101000 А |
| СВИ 1100100 К | 10001 плюс 11001 равно 101010 |
Выполните вычисления и запишите ответ в десятичной системе счисления:
| 1) | 100 2 ·5 8 = |
| 2) | 100 3 + 100 5 = |
| 3) | 10 9 ·10 100 – 10 900 = |
| 4) | 33 4 + 44 5 = |
| 5) | 15 6 + 51 8 = |
Переведите заданные числа в указанные системы счисления:
| Число 10 | Число 5 | Число 4 | Число 3 | Число 2 |
|---|---|---|---|---|
| 1) | 0 | |||
| 2) | 1 | |||
| 3) | 2 | |||
| 4) | 3 | |||
| 5) | 4 | |||
| 6) | 5 | |||
| 7) | 9 | |||
| 8) | 16 | |||
| 8) | 25 | |||
| 9) | 32 | |||
| 10) | 64 |
Вариант 2
Запишите арифметическое выражение для решения следующей задачи и подсчитайте ответ:
| Наша умница Мальвина Опекает Буратино И купила для него, Что ему нужней всего: 10 2 обложки, 11 2 линейки И на 111 2 рублей наклейки. На обложках Бармалей, Цена каждой 101 2 рублей. На линейки, что купила, 101010 2 рубля хватило. Сколько стоили покупки? На раздумье полминутки. |
Попробуйте использовать стандартную программу Калькулятор для перевода чисел из стихотворения в привычную десятичную запись ( Вид Инженерный, Bin двоичное представление числа, Dec десятичное представление числа). Запишите алгоритмы перевода чисел с помощью Калькулятора из двоичного представления в десятичное и наоборот, из десятичного в двоичное.
Вариант 3
Докажите, что запись 10 в любой позиционной системе счисления означает число, равное основанию этой системы.
Определите основание позиционной системы счисления для каждого равенства.
Шестнадцатеричная система счисления использует 16 цифр. Первые десять цифр совпадают с цифрами десятичной системы, а последние обозначаются буквами латинского алфавита:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
| Цифра | Значение |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
A8 16 = 10 ·16 + 8 ·1 = 168 10
В каждом задании найдите значение числа x.
Выполните следующие задания.
Сформулировать алгоритм перевода числа из десятичной в троичную систему счисления.
Построить таблицы сложения и умножения для четверичной системы счисления. Пользуясь этими таблицами выполнить столбиком следующие действия над числами (оставаясь в четверичной системе счисления):
Построить таблицы сложения и умножения для двоичной системы счисления. Пользуясь этими таблицами выполнить столбиком следующие действия над числами (оставаясь в двоичной системе счисления):
Системы счисления. Основные понятия.
Запись числа в некоторой системе счисления называется кодом числа.
Количество разрядов в записи числа называют разрядностью и совпадает с его длиной.
Системы счисления делятся на позиционные и непозиционные. Позиционные системы счисления делятся
на однородные и смешанные.
Непозиционная система счисления — древнейшая, здесь все цифры числа имеют величину, которая не
зависит от позиции (разряда).
Т.е., если есть 5 палочек, значит число соответственно равно 5, так как каждой палочке, вне зависимости
от её места в строке, соответствует только 1 предмет.
Позиционная система счисления — значение каждой цифры зависит от позиции (разряда) этой цифры в числе.
Например, стандартная 10-я система счисления является позиционной. Допустим дано число 453.
Цифра 4 означает число сотен и соответствует числу 400, 5 — кол-во десятков и соответствует значению
50, а 3 — единицы и значению 3. Легко заметить, что с увеличением разряда увеличивается значение.
Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Однородная система — для каждого разряда (позиции) числа набор допустимых символов (цифр)
одинаковый. Как пример снова используем 10-ю систему. Если записывать число в однородной 10-й системе,
(1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, так как символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может
отличаться от наборов в других разрядах. Хороший пример — система измерения времени. В разряде
В непозиционных системах счисления вес цифры не зависим от позиции, которую она занимает в
числе. К примеру, в римской системе счисления в числе XXXII (32) вес цифры X в каждой позиции
Цифрами в римской системе служат: I(1), V(5), X(10), L(50), C(100), D(500), M(1000).
Размер числа в римской системе счисления определяют как сумму либо разность цифр в числе. Когда
меньшая цифра стоит слева от большей – она вычитается, когда справа – прибавляется.
Самая первая система счисления — единичная (непозиционная).
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в
последовательности цифр, которые изображают число.
Каждая позиционная система характеризуется своим основанием.
Основание позиционной системы счисления – это количество разных знаков либо символов, которые
используются для изображения цифр в этой системе.
множество позиционных систем.
Перевод систем счисления. Числа можно перевести из одной системы счисления в другую.
Таблица соответствия цифр в различных системах счисления.
Применение двоичной логики в недвоичных операциях: оптимизируем производительность и ресурсы
Поговорим о побитовых операциях.
С ними привычно иметь дело embedded-разработчикам и тем, кто занимается криптографией. Также побитовые операции можно встретить в системном программировании, компьютерной графике и везде, где присутствует сильная ограниченность ресурсов или длительные вычисления.
В прикладном же программировании многие устанавливают (|) и проверяют параметры (&) через степени двойки. Как правило, дальше этого не заходит. Но всегда есть задачи, которые потребуют горизонтального масштабирования при высокой нагрузке в случае их решения явным или привычным способом.
Попробуем применить побитовые операции к прикладной задаче для оптимизации кода в плане производительности и используемых ресурсов – и посмотрим, что из этого получится.
Побитовые операции: вспомним основы
Побитовые операторы производят операции, используя двоичное представление числа. Среди наиболее частых случаев использования побитовых операций – такие:
Включение бита: y = x | (1 x = x ^ y ^ x
Также достаточно просто умножать и делить на степени двойки. Для этого достаточно сдвинуть число вправо или влево. Например, умножение числа 10 на 2: 10
Задача: приоритизировать данные на основе рейтинга (веса), полученного при объединении ключевых характеристик, с учётом важности каждой из них.
Рассмотрим эту задачу на примере моделей товара. Пусть набор множества неограниченного количества характеристик на входе даёт свёртку взвешенных сумм на выходе. Предположим, это будут пять ключевых характеристик: X1, X2, X3, X4, X5. С точки зрения пользователя это информация о цвете, материале, размере жесткого диска и т.д. Нормализованный вес характеристик определяется значениями от 0 до 10 – например, 7, 10, 5, 8, 9. При составлении рейтинга также имеет значение порядок данных характеристик.
Выделим по 4 бита на каждое значение, так как 10 в двоичном исчислении – 1010; соответственно, все числа меньше 10 также не выйдут за пределы четырёх битов.
Объединим полученные данные в одно значение:
То есть через операторы | и 2 ).
Стоило ли оно того? Например, мы могли с помощью ML получить какую-то одну вероятностную характеристику и пользоваться ей. Но всё-таки набор характеристик, хранящихся в одном месте, – лучше, чем одно весовое значение. Так мы получим преимущество пересчёта рейтинга на лету при изменении приоритета характеристик пользователем. Рассмотрим следующий пример.
Побитовые сдвиги для задачи рекомендации товаров из смежных категорий
Теперь в нашем примере у каждой модели есть значение рейтинга или вес. Предположим, пользователь добавил в избранное то, что ему понравилось. Дальше он может переопределить при необходимости порядок характеристик в соответствии со своими предпочтениями. В этом случае результирующее значение рейтинга будет пересчитано. Далее мы можем пересчитать рейтинг смежных категорий в соответствии с выбранным пользователем приоритетом характеристик и предложить ему те товары, которые близки или выше по рейтингу.
Рассмотрим на примере. Допустим, пользователь выбрал смартфон со следующим приоритетом характеристик по умолчанию:
1. Объем жесткого диска (8).
Данные характеристики представлены в виде вычисленного числового значения. Далее пользователь может переопределить их порядок, если посчитает более важным для себя “Цвет”, например. Или полностью опустить какую-то из характеристик. И затем происходит поиск моделей, которые находятся в том же каталоге. У них в свою очередь пересчитаются веса в соответствии с выбранным новым приоритетом. И в конце происходит их сортировка — с целью предложить пользователю что-то близкое.
В этой задаче можно применить побитовые операции и к поиску. Рассмотрим категоризацию. Попробуем найти модели из смежных категорий, используя побитовые сдвиги.

Предположим для простоты, что вложенность категорий не больше четырёх. Соответственно, можно выделить 2 16 = 65536 идентификаторов категорий для числа разрядности 64. Используем что-то вроде внутреннего идентификатора, а не идентификаторы из базы данных, во избежание переполнения накопителя.
Точно так же, как и в предыдущем примере, сохраним путь категории в результирующее значение. Можно заметить, что дерево категорий укладывается в следующее представление:
Например, для категории 401 полный путь вычисляется так:
Также вычисление можно представить в виде:
Если пользователь выбрал одноместную палатку, то будем предлагать ему что-то аналогичное – тоже палатки: двухместные, трёхместные и далее по списку.
По рисунку видно, что у дерева категорий есть общая часть, которая не нужна для сокращения количества лишних переборов и проверок наличия реальных моделей, привязанных к той или иной категории. Чтобы отбросить общую часть, нужно знать значение позиции, относительно которой мы будем оставлять то, что нам нужно, или, наоборот, отбрасывать.

Данное значение можно вычислить, но желательно знать заранее. Можно такие значения хранить отдельно, а можно – в значении вычисленного пути, выделив для него два бита.
Нам заранее известно, сколько слотов выделено для одной категории (16), поэтому для вычисления той или иной позиции достаточно хранить только количество сдвигов. В нашем случае достаточно хранить числа от 0 до 3, которым вполне хватит двух битов.
Предположим, мы получили нужное значение. Для категории 401 оно будет равно числу 1. Таким образом, дальнейшие операции будут производиться со следующей позиции:
Далее по общей части родительских категорий можно найти в базе данных смежные категории. Для этого создадим маску совпадения в данном случае первых двух родительских категорий:
Выполняем запрос для выборки категорий со следующим условием:
Это даст нам список смежных категорий за одно обращение к хранилищу данных без последующего перебора и анализа связей.
А далее из списка полученных значений извлекаем, наоборот, не родительские категории, а те, которые будут содержать списки других потенциально релевантных моделей.
Интересующие нас значения:
То есть обнуляем родительские категории, сдвигая число к правой границе на 32 бита. Оставшееся значение в свою очередь разбивается по 16 битов. И на выходе уже получаем значения идентификаторов 301, 302, 303, 401, то есть категорий, по которым будет произведён поиск моделей.
В итоге необходимые значения быстро определяются и нет необходимости выгружать ненужные записи для определения местоположения в иерархии дерева категорий.
Сортировка и побитовые операции
Попробуем приблизительно оценить встроенную сортировку (O(n 2 )), сортировку слиянием (merge sort) (O(n log n)) и поразрядную сортировку (radix sort) с побитовыми операциями. Опускаем при этом свою реализацию быстрой сортировки для целочисленных значений по двум причинам. Во-первых, сложность сортировки слиянием в худшем случае лучше. И выполняется быстрее на больших объемах сортируемых данных. Во-вторых, даже при каком-то улучшении для прикладной задачи не имеет большого смысла реализовывать быструю сортировку параллельно со встроенным вариантом.
Генерируем 1000000 чисел и запускаем алгоритмы сортировки:
Можно увидеть, что в среднем время работы сортировки с использованием побитовых операций на больших данных сопоставимо с сортировкой слияния, но вторая значительно проигрывает в плане потребления ресурсов.
Вернемся к прикладной задаче. Теперь мы знаем, как при помощи побитовых операций можно ранжировать данные по разным признакам, учитывая приоритет каждого из них. То же самое можно сделать при помощи обычных циклов.
В таком случае более привычная реализация через циклы оказывается задачей более сложной. На первом этапе сортируем значения с самым высоким приоритетом, а далее при переходе на каждое последующее значение с более низким приоритетом учитываем предыдущую сортировку. То есть каждая последующая операция осуществляется в своей группе.
Посмотрим на производительность каждого из алгоритмов. Для этого загрузим данные из файла в количестве 10000 записей следующего вида:
И запустим алгоритмы:
Циклы и побитовые операции
Результаты выполнения работы алгоритмов следующие:
Результаты тестирования показывают, что ранжирование данных при помощи циклов значительно уступает по производительности.
Побитовые операции – не только для низкоуровневого программирования
Побитовые операции можно использовать в прикладном программировании. Конечно, такой код требует особой аккуратности при разработке и поддержке и по большому счёту оправдан, когда это действительно нужно. Если его изолировать и не смешивать с основной бизнес-логикой, то не всё так страшно, как может показаться на первый взгляд. Выигрыш во временном отношении может быть при этом значительным – может более, чем на порядок превосходить обычные циклы.
В примере выше сохранение значений рейтинга в одну переменную значительно сократит используемые ресурсы, а его вычисление заменит вложенные циклы.
Сохранение пути категории позволяет хранить состояние некоторой части системы. Тем самым снижается количество запросов и нет необходимости выгружать все категории для анализа с целью определения местоположения в иерархии дерева категорий.
Что касается алгоритмов сортировки, то важно учитывать, какие данные сортируются и для какого объёма входящих данных делается сортировка. Результаты тестирования показывают, что сортировка слиянием и поразрядная сортировка примерно одинаковы в плане производительности. Но при этом потребление ресурсов у первой значительно выше.
Напоследок — список возможностей побитовых операций, которые могут пригодиться на практике:
оптимизация распространённых операций: хранение опций в одной переменной, также определение чётности/нечётности, обмен значений переменных, приведение к верхнему/нижнему регистру и т. д.;
более оптимальное использование памяти;
использование в алгоритмизации – с целью оптимизации узких мест: замена дорогих операций умножения и деления и т. д.;
возможность сохранения состояния какой-либо части системы в более компактном виде.