Что такое видовое понятие и родовое
§ 7. Родовые и видовые понятия
Мы уже знаем, что как в процессе ограничения, так и в процессе обобщения получается ряд понятий, из которых одни являются менее общими, а другие более общими. Более общие понятия называются родовыми понятиями, менее общие — видовыми понятиями.
Возьмём ряд понятий: «город» — «столица» — «Москва». Понятие «город» будет родовым по отношению к понятию «столица», а понятие «столица» будет родовым по отношению к понятию «Москва». Но эти же понятия находятся и в другом отношении: понятие «Москва» является видовым по отношению к понятию «столица», а понятие «столица» является видовым по отношению к понятию «город».
Таким образом, одно и то же понятие в одно и то же время может быть и видовым, и родовым, но только в разных отношениях: по отношению к менее общему — оно родовое, а по отношению к более общему — видовое. В приведённом выше примере понятие «столица» является видовым по отношению к понятию «город» и родовым по отношению к понятию «Мосрсва».
Родовое понятие (или род) не может существовать отдельно от видовых понятий, а видовые понятия (или виды) не могут существовать отдельно от рода. Род и вид всегда взаимно связаны.
Эта взаимная связь рода и вида отражает существующую в предметах связь общего и отдельного, а именно: каждый предмет объективного мира содержит в себе и общие свойства, которые объединяют его с однородными предметами, и свои, особые свойства.
Например, яблоко есть плод (общее свойство, присущее яблокам и другим плодам), но яблоко имеет также свои, особые свойства, которых нет у других плодов; сосна есть дерево (общее свойство), но сосна имеет и свои, особые свойства, присущие только сосне и отличающие её от других деревьев.
Общие свойства существуют только в отдельных предметах. Тем самым общие свойства являются признаком отдельных предметов.
Так как всякое яблоко есть плод, то «плод» есть признак яблока; «дерево» есть признак сосны и т д. Причём эти общие свойства (плод, дерево) являются существенными признаками, так как они выражают коренные свойства предметов.
Точно так же родовые понятия, отражая объективную связь предметов и явлений действительности, являются признаками своих видов.
Когда мы говорим «химия есть наука», то мы указываем, к какому роду относится «химия» (к роду «наука»), и в то же время указываем существенный признак «химии», её родовой признак («наука»).
Глава III. Содержание и объём понятий
Признаки понятий. Понятия в психологии получаются из сравнений сходных представлений. Представления в свою очередь складываются из отдельных элементов. Составные элементы представления или понятия принято называть признаками. Признаки есть то, чем одно представление или понятие отличается от другого. Например, признаками золота мы считаем «металл», «драгоценный», «имеющий определённый удельный вес» и т.п. Это всё то, чем золото отличается от других вещей, от не-металлов, от недрагоценных металлов и т.п.
Не все признаки нужно считать равноценными. Каждое понятие имеет множество различных признаков, но при мышлении о нём мы прежде всего по преимуществу мыслим только известные признаки. Эти признаки являются как бы основными, около которых группируются другие признаки. Первые признаки называются существенными, или основными, а остальные – второстепенными. Основные признаки – это такие признаки, без которых мы не можем мыслить известного понятия и которые излагают природу предмета. Например, для ромба существенным является тот признак, что он есть четырёхугольник с параллельными и равными сторонами и т.п.; несущественным для понятия ромба является тот признак, что он имеет ту или другую величину сторон, ту или другую величину углов.
Признаки понятий со времени Аристотеля принято делить на следующие 5 классов:
1. Родовой признак. Если мы скажем, что химия есть наука, то наука будет родовым признаком для понятия «химия»; в числе других признаков, присущих понятию «химия», есть и признак «наука»; этот признак отличает химию от всего, что не есть наука. Род (genus) или родовой признак есть понятие класса, в который мы вводим другое рассматриваемое нами понятие.
2. Видовое различие. Если мы скажем, что химия есть наука, занимающаяся изучением строения вещества, то прибавление признака – «занимающаяся изучением строения вещества» будет служить для обозначения того, чем эта наука отличается от других наук. Такой признак, который служит для того, чтобы выделять понятие из ряда ему подобных понятий, называется видовым различием (differentia specifica). Возьмём понятия «моряк русский», «моряк французский», «моряк английский». В этом случае «русский», «французский», «английский» есть видовое различие; оно служит для того, чтобы выделить моряка одной нации от моряков всех прочих наций.
3. Вид (species). Если к родовому признаку присоединить видовое различие, то получится вид. Например, «здание для склада оружия» – арсенал; «здание для склада хлеба» – амбар. В этом случае «здание» есть род, «для хранения оружия» есть видовое различие; присоединение к роду видового различия даёт вид «арсенал». Присоединение к понятию «здание» видового признака «служащее для хранения хлеба» даёт вид «амбар». Вид может быть признаком, потому что его можно приписать понятию. Например, «эта наука есть химия».
4. Собственный признак (proprium). Собственный признак – это такой признак, который присущ всем вещам данного класса, который не содержится в числе существенных признаков, но который может быть выведен из них. Например, существенным признаком человека является его «разумность». Из этого свойства вытекает его способность владеть речью. Этот последний признак есть собственный признак. Основной признак треугольника – это прямолинейная плоская фигура с тремя сторонами. Что же касается того признака треугольника, что сумма углов его равняется двум прямым, то это есть его собственный признак, потому что вытекает или выводится из основных признаков. Мы этого признака не мыслим, когда думаем о треугольнике, поэтому он является выводным.
5. Несобственный признак (accidens). Несобственный признак – это такой признак, который не может быть выведен из существенного признака, хотя и может быть присущ всем вещам данного класса. Например, чёрный цвет ворона есть accidens. Если бы чёрный цвет ворона был выводим из основных свойств его, то он мог бы быть назван proprium, но он не выводим, так как мы не знаем, по какой причине вороны имеют чёрный цвет перьев. Он есть, следовательно, accidens.
Несобственные признаки делятся на две группы: на неотделимые несобственные признаки (accidens inseparabile) и отделимые несобственные признаки (accidens separabile). Последние суть те признаки, которые присущи только некоторым вещам того или другого класса, но не всем, а первые присущи всем вещам данного класса. Например, чёрный цвет ворона есть accidens inseparabile. Чёрный цвет волос для человека есть accidens separabile, потому что есть люди, которые не имеют чёрного цвета волос. По отношению к отдельным индивидуумам несобственный признак также может быть отделимым и неотделимым. Отделимые – это такие признаки, которые одно время имеются налицо, а в другое время не имеются. Например, Бальфур – первый министр Англии. Через некоторое время он может не быть первым министром. Это есть признак отделимый. «Лев Толстой родился в Ясной Поляне». В этом предложении признак «родился в Ясной Поляне» есть неотделимый признак.
Содержание и объём понятий. Понятия могут быть рассматриваемы с точки зрения содержания и объёма.
Содержание понятия – это то, что мыслится в понятии. Например, в понятии «сахар» мыслятся признаки: сладкий, белый, шероховатый, имеющий тяжесть и т.д.; эти признаки в совокупности и составляют содержание понятия «сахар». Содержание понятия, другими словами, есть сумма признаков его; поэтому каждое понятие можно разложить на ряд присущих ему признаков. Содержание понятия может быть весьма изменчивым в зависимости от принятой точки зрения, от размера знания и т.п. Например, в понятии «сахар» химик мыслит одно содержание, а нехимик – другое.
Объём понятия есть то, что мыслится посредством понятия, т.е. объём понятия есть сумма тех классов, групп, родов, видов и т.п., к которым данное понятие может быть приложено. Например, объём понятия «животное»: птица, рыба, насекомое, человек и т.д.; объём понятия «элемент»: кислород, водород, углерод, азот и т.д.; объём понятия «четырёхугольник»: квадрат, прямоугольник, ромб, трапеция.
Таким образом, различие между объёмом понятия и содержанием понятия сводится к следующему: объём понятия означает ту совокупность предметов, к которым должно прилагаться данное понятие, а содержание обозначает те признаки, которые приписываются тому или другому понятию.
Для более ясного представления объёма понятий и отношения объёмов существует особый приём, называемый «логической символикой».
На рис. 1 большой круг символизирует собой понятие «элемент», а меньшие круги, в нём находящиеся, символизируют понятия, входящие в его объём. Если мы изображаем какой-нибудь круг внутри другого круга, то мы этим символизируем, что объём одного понятия входит в объём другого.
Из рис. 2 видно, что понятие «дерево» содержит в своём объёме понятия «дуб», «ель» и т.п. Отдельные точки в круге «ель» символизируют индивидуальные, или единичные, ели.
Понятие с большим объёмом называется родом по отношению к тому понятию с меньшим объёмом, которое входит в его объём. Понятие с меньшим объёмом в этом случае называется видом. Понятия с большим объёмом можно назвать также понятиями более широкими или более общими.
Любой вид может сделаться родом. Например, понятие «пальма» относится к понятию «дерево», как вид к роду, но в свою очередь оно относится уже как род к своим видам – «пальма кокосовая», «пальма фиговая» и т.д. Вообще более общее понятие есть род для менее общего понятия; более общее понятие представляет собой родовое понятие для менее общего, менее общее само становится родом для ещё менее общего и т.д., пока мы не придём к такому понятию, которое уже не может в своём объёме содержать какие-либо другие виды, а может подразделяться только на отдельные индивидуумы.
Следует упомянуть о попытке греческого философа Порфирия (233–304) при помощи схемы облегчить понимание отношения между охватывающими друг друга понятиями, т.е. понятиями, из которых одно входит в объём другого. Эта схема называется «деревом Порфирия». В понятие «бытия» (т.е. того, что вообще существует) входит понятие «телесного бытия» и «бестелесного бытия». Тело содержит в своём объёме одушевлённое тело, или организм, и неодушевлённое тело. Понятие «организм» содержит в своём объёме чувствующие и нечувствующие организмы (растения). Чувствующие организмы содержат в своём объёме разумные и неразумные существа и т.д. (рис. 3).
Бытие есть высший род, который уже не может быть видом для другого рода. Такой род называется summum genus; человек – это низший вид. В его объём уже не входят понятия с меньшим объёмом, а входят только отдельные индивидуумы. Такое понятие называется infima species (самый низший вид). Ближайший высший класс (или род) того или другого вида называется proximum genus (ближайший род). Отношение между более широкими и узкими понятиями можно изобразить и иначе, именно, поместив круги, служащие для обозначения понятий с меньшим объёмом, внутри кругов, служащих для обозначения понятий с большим объёмом (рис. 3а).
Ограничение и обобщение. Процесс образования менее общих понятий из более общих называется ограничением (determinatio). Для образования менее общего понятия мы должны к более общему прибавить несколько признаков, благодаря чему понятие уясняется (determinatur). Например, чтобы из понятия «дерево» получить менее общее понятие «пальма», надо к признакам дерева прибавить специальные признаки пальмы: вид её листьев, прямизну ствола и т.д. Обратный процесс образования более общего понятия из менее общего, при котором, наоборот, некоторое количество признаков от данного понятия отнимается, называется обобщением (generalisatio).
Род образуется из видов при помощи процесса обобщения, и, наоборот, виды образуются из родов при помощи процесса ограничения. Эти процессы мы можем изобразить при помощи следующей схемы:
Предположим, что у нас есть понятие A (наука). Из него при помощи видового различия a мы можем образовать вид Aa (математика); прибавив к понятию Aa видовое различие b (определение пространственных отношений), получим геометрию Aab. Прибавив к этому виду признак c (определение пространственных отношений на плоскости), получим планиметрию Aabc.
Обратный процесс – получение более общих понятий путём отбрасывания отдельных признаков – будет называться обобщением. И тот и другой процесс можно изобразить при помощи следующей схемы, в которой стрелки показывают или нисхождение от более общих понятий к менее общим или, наоборот, восхождение от менее общих к более общим понятиям.
Отношение между объёмом и содержанием понятия. Для того чтобы ответить на вопрос, какое существует отношение между объёмом и содержанием понятия, возьмём какой-нибудь пример. Объём понятия «человек» обширнее, чем, например, объём понятия «негр». Употребляя понятие «человек», мы думаем обо всех людях, мы думаем о людях, живущих во всех пяти частях света, между прочим и в Африке. Употребляя понятие «негр», мы думаем только о тех людях, которые живут в Африке. Но о содержании этих двух понятий следует сказать как раз наоборот: содержание понятия «негр» будет обширнее содержания понятия «человек». Когда мы говорим о негре, то мы можем найти в нём все признаки понятия «человек» плюс ещё некоторые особенные признаки, как-то: чёрный цвет кожи, курчавые волосы, приплюснутый нос, толстые губы и т.п.
Итак, по мере увеличения содержания понятия уменьшается его объём, и наоборот.
Вопросы для повторения
Что такое признаки понятий? Какие признаки понятий мы отличаем? Что такое родовой признак? Что такое видовое различие? Что такое вид? Что такое собственный признак? Что такое несобственный признак? Что такое содержание понятия? Что такое объём понятия? Что такое summum genus? Что такое infima species? Что такое обобщение? Что такое ограничение? Какое существует отношение между объёмом и содержанием понятия?
Логика. Учебник для средней школы.
Глава III
ПОНЯТИЕ
§ 5. Соотношение между содержанием и объёмом понятия
Между содержанием и объёмом понятия существует определённое соотношение. Рассмотрим это соотношение на примере.
В объём понятия «позвоночные» входят все виды позвоночных животных, а содержанием являются существенные признаки, общие для всех позвоночных. Возьмём понятие, меньшее по объёму: «млекопитающие». В объём этого понятия входят не все виды позвоночных, а только часть их, следовательно, объём понятия будет меньше.
Однако содержание понятия расширяется за счёт новых признаков. Понятие «млекопитающие» содержит в себе признаки позвоночных (всякое млекопитающее есть позвоночное), а кроме того, оно содержит ещё свои, особые признаки (кормление детёнышей молоком и др.), которых не было в содержании понятия «позвоночные».
Другой пример: всякая берёза есть дерево, следовательно, понятие «берёза» содержит в себе все признаки понятия «дерево». Но берёза имеет ещё и свои, особые признаки, следовательно, в содержании понятия «берёза» признаков больше, чем в содержании понятия «дерево». Однако по объёму понятие «берёза» уже, чем понятие «дерево».
Итак, понятия, более широкие но объёму, являются более узкими по содержанию — такова зависимость между содержанием и объёмом понятий. Эта зависимость имеет значение закона, который называется законом обратного отношения содержания и объёма понятий. Формулировка закона следующая:
чем шире содержание понятия, тем уже его объём. И соответственно наоборот: чем уже содержание понятия, тем шире его объём.
Закон «обратного отношения» распространяется только на такие понятия, из которых одно входит в объём другого.
Однако из данного закона не следует, что более широкие по объёму, т. е. более общие, понятия имеют для нас меньшую ценность. Общие понятия отображают общие свойства, связи и закономерности предметов и явлений объективного мира.
§ 6. Ограничение и обобщение понятия
В практике мышления мы нередко пользуемся логическими приёмами, которые называются обобщением понятия и ограничением понятия.
Обобщить понятие — это значит перейти от менее общего к более общему понятию.
Ограничить понятие — это значит перейти от более общего понятия к менее общему понятию.
В соответствии с этим (согласно «закону обратного отношения») изменяется содержание понятия.
Рассмотрим процесс ограничения понятия на следующем примере. Объяснение того, что такое натрий, можно начать с напоминания о том, что представляет собой вообще элемент, а затем в понятие «элемент» ввести некоторые признаки, свойственные металлу. Введение этих признаков сузит объём понятия «элемент», ограничит объём этого понятия, тем самым получится другое понятие, с меньшим объёмом, — понятие «металл».
Далее, вводя в понятие «металл» признаки, свойственные натрию, мы тем самым ограничиваем понятие «металл», т. е. даём вместо него ещё менее общее понятие — «натрий».
Таким образом, процесс ограничения понятия представляет собой постепенный переход от более общих понятий к менее общим.
Ограничением понятий мы пользуемся в тех случаях, когда разъясняем содержание какого-либо понятия, причём строим своё разъяснение на основе уже известных, более общих понятий.
Ограничение понятия применяется также в тех случаях, когда бывает необходимо уточнить содержание понятия, указать, к какому именно кругу явлений относится данное понятие, следовательно, отграничить понятие от других понятий, в том числе и от более общих.
В процессе ограничения понятий, переходя от более общих понятий к менее общим, мы приходим, наконец, к таким понятиям, объём которых равен единице и которые, следовательно, не могут подлежать дальнейшему ограничению. Такие понятия отражают единичные, индивидуальные предметы и являются предельно узкими по объёму.
Примеры таких понятий: «Каспийское море», «первая мировая война 1914 года», «улица Горького в Москве».
Обобщение понятия представляет собой процесс, обратный ограничению. При обобщении понятия путём исключения некоторых его признаков мы переходим от менее общих ко всё более и более общим понятиям. Например, от понятия «чех» — к понятию «славянин», от понятия «славянин» — к понятию «человек».
Процесс обобщения понятия протекает на основе того, что круг рассматриваемых нами предметов всё более и более расширяется за счёт новых, отличных по своим свойствам предметов.
Обобщая понятия, переходя от менее общих к более общим, мы приходим, наконец, к предельно широким по объему понятиям, которые не подлежат дальнейшему обобщению.
Примеры категорий: «материя», «время», «движение», «пространство», «количество», «форма» и др.
§ 7. Родовые и видовые понятия
Возьмём ряд понятий: «город» — «столица» — «Москва». Понятие «город» будет родовым по отношению к понятию «столица», а понятие «столица» будет родовым по отношению к понятию «Москва». Но эти же понятия находятся и в другом отношении: понятие «Москва» является видовым по отношению к понятию «столица», а понятие «столица» является видовым по отношению к понятию «город».
Таким образом, одно и то же понятие в одно и то же время может быть и видовым, и родовым, но только в разных отношениях: по отношению к менее общему — оно родовое, а по отношению к более общему — видовое. В приведённом выше примере понятие «столица» является видовым по отношению к понятию «город» и родовым по отношению к понятию «Москва».
Родовое понятие (или род) не может существовать отдельно от видовых понятий, а видовые понятия (или виды) не могут существовать отдельно от рода. Род и вид всегда взаимно связаны.
Эта взаимная связь рода и вида отражает существующую в предметах связь общего и отдельного, а именно: каждый предмет объективного мира содержит в себе и общие свойства, которые объединяют его с однородными предметами, и свои, особые свойства.
Например, яблоко есть плод (общее свойство, присущее яблокам и другим плодам), но яблоко имеет также свои, особые свойства, которых нет у других плодов; сосна есть дерево (общее свойство), но сосна имеет и свои, особые свойства, присущие только сосне и отличающие её от других деревьев.
Общие свойства существуют только в отдельных предметах. Тем самым общие свойства являются признаком отдельных предметов.
Так как всякое яблоко есть плод, то «плод» есть признак яблока; «дерево» есть признак сосны и т д. Причём эти общие свойства (плод, дерево) являются существенными признаками, так как они выражают коренные свойства предметов.
Точно так же родовые понятия, отражая объективную связь предметов и явлений действительности, являются признаками своих видов.
Когда мы говорим «химия есть наука», то мы указываем, к какому роду относится «химия» (к роду «наука»), и в то же время указываем существенный признак «химии», её родовой признак («наука»).
§ 8. Основные классы понятий
По своему объёму понятия делятся на единичные и общие.
Единичные понятия являются понятиями об отдельных (единичных) предметах.
Примерами таких понятий могут быть следующие: «полководец М. И. Кутузов», «город Ленинград», «Народно-Демократическая Республика Болгария», «самое глубокое озеро в мире».
В общих понятиях отображается множество однородных предметов.
Например: «звезда», «книга», «школа», «песня», «урожай» и др.
Каждое из этих понятий относится к большой группе однородных предметов.
Общие понятия могут быть более общими и менее общими. Так, понятие «трактор» является менее общим по отношению к понятию «сельскохозяйственная машина», но более общим по отношению к понятию «гусеничный трактор».
Число предметов, которые охватываются общим понятием, может быть ограниченным или неограниченным. Например, общее понятие «корабль» относится ко всем кораблям, которые были, есть и будут.
К общим понятиям с ограниченным объёмом относятся такие понятия: «станции Московского метро первой очереди», «произведения Лермонтова», «учёные XIX века».
Общие и единичные понятия могут быть собирательными понятиями.
Собирательные понятия — это такие понятия, в которых мыслится совокупность однородных предметов как единое целое.
Например: «лес» (деревьев), «библиотека» (книг), «собрание» (учеников).
Особенность собирательных понятий заключается в том, что их нельзя приложить к отдельным предметам, совокупность которых мыслится в данном собирательном понятии. Нельзя, например, отнести понятие «лес» к отдельному дереву, понятие «собрание» к отдельному ученику.
Собирательные понятия можно приложить или к совокупности предметов как единому целому, или к ряду таких совокупностей. В первом случае будет единичное собирательное понятие, во втором случае — общее собирательное понятие.
Например, понятие о Государственной библиотеке имени В. И. Ленина в Москве будет единичным собирательным понятием, а понятие о библиотеке (вообще) будет общим собирательным понятием, так как оно относится ко многим библиотекам.
Примеры общих собирательных понятий: «группа», «созвездие», «коллектив», «полк», «народ», «толпа», «класс» и др. Примеры единичных собирательных понятий: «созвездие Большая Медведица», «коллектив служащих (такого-то) учреждения», «рабочий класс демократической Польши».
Каждое понятие находится в различных отношениях с другими понятиями и поэтому одновременно входит в разные классы.
Например, понятие «высота» есть общее, несобирательное; понятие «собрание» — общее, собирательное; понятие «единство стиля и содержания в рассказах А. П. Чехова» — единичное, собирательное.
Отношения между понятиями
Урок 12. Информатика 4 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Отношения между понятиями»
Не успел я вас познакомить со своим приятелем Аркадием, он опять исчез. Каждый раз, когда я пытаюсь объяснить ему тему «Отношения между понятиями» происходит одно и тоже – Аркадий просто исчезает. Я понимаю, тема сложная, но неужели я так плохо объясняю?! А может это просто он ленится понимать.
Итак, знакомясь с этой темой, мы рассмотрим отношения между понятиями: «вид ↔ вид», «род → вид», «вид ← род».
Научимся узнавать и называть отношения. И будем строить схемы отношений в виде кругов Эйлера.
С профессором Знатоковым вы уже выясняли, что объекты реальной действительности находятся в определённых отношениях между собой. Например:
И знаете, что отношения между объектами бывают симметричными и несимметричными.
Так вот, понятия, так же, как и объекты, находятся в определённых отношениях между собой.
Давайте рассмотрим это на примере знаков. Знаки бывают разными: цифры, буквы, знаки препинания, знаки арифметических действий, иероглифы, дорожные знаки и другие.
Как мы помним, знак – это родовое понятие. А цифра, буква, знак препинания, знак арифметических действий, иероглиф, дорожный знак – это видовые понятия.
Давайте рассмотрим отношения между понятиями в таблице.
В первом столбце запишем первое понятие. В третьем столбце – второе понятие. А во втором – отношение между этими понятиями.
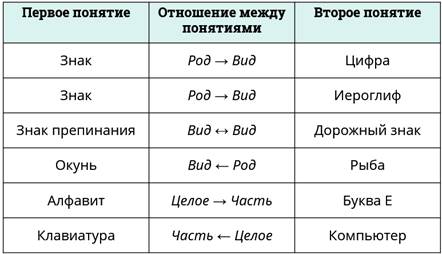
Итак, первая пара понятий: знак, цифра. Знак – это родовое понятие, цифра – это видовое понятие. Значит, отношение род → вид.
Вторая пара понятий: знак, иероглиф. Знак – это родовое понятие, иероглиф – это видовое понятие. Отношение опять род → вид.
Следующая пара: знак препинания, дорожный знак. Оба эти понятия относятся к видовому понятию. Значит, отношение между ними вид ↔ вид.
Пара отношений: окунь, рыба. Окунь – это видовое понятие, рыба – родовое. Значит, отношение вид ← род.
Мы получили отношения: род → вид, вид ↔ вид и вид ← род. Ещё между понятиями могут быть и другие отношения, такие как: целое → часть и часть ← целое.
Помните, между объектами тоже встречались такие отношения?
Вот пара понятий: алфавит, буква Е. Алфавит, конечно, это целое, а буква Е – часть. Значит отношение между ними целое → часть.
Клавиатура, компьютер. Отношение между ними часть ← целое.
Обратите внимание на то, что линия со стрелкой начинается от отношений «род» и «целое» и указывает на отношения «вид» и «часть».
Отношения между понятиями бывают несимметричными и симметричными.
Ребята, запомните, что несимметричные отношения обозначают однонаправленной стрелкой, а симметричные – двунаправленной стрелкой.
Симметричные отношения – это отношения между понятиями одного уровня. Например, между видовыми понятиями.
Давайте рассмотрим вот такую схему и расставим в ней отношения между понятиями в виде стрелок.
Между понятиями «знак» и «буква» отношение род → вид, стрелка одностороння и направлена от родового понятия к видовому. Между понятиями «знак» и «цифра» всё аналогично.
«Буква» и «цифра» – понятия одного уровня, поэтому отношение между ними симметричное вид ↔ вид и стрелка двусторонняя. Такое же симметричное отношение и между понятиями «буква Л» и «буква Д» и «цифра 7» и «цифра 3».
А вот отношение между понятиями «буква» и «Буква Л» и «буква» и «Буква Д» несимметричное род → вид.
Тоже самое можно сказать и про отношения между понятиями «цифра» и «цифра 7» и «цифра» и «цифра 3».
Я читал, что если понятия при симметричных отношениях поменять местами, то название отношения не изменится. Давайте проверим, так ли это.
Поменяем буквы местами между собой, а цифры. Отношения не изменились, как были симметричные, так и остались.
А если поменять вот так тоже всё по-прежнему. Между понятиями «цифра» и «буква» отношение симметричное.
Предлагаю сейчас закрепить полученные знания, дописав в таблицу отношения между предложенными понятиями.
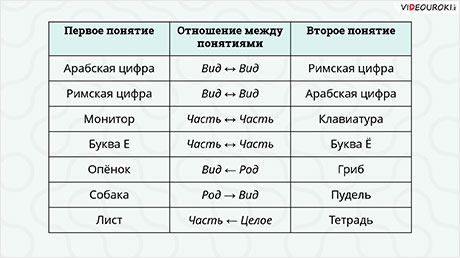
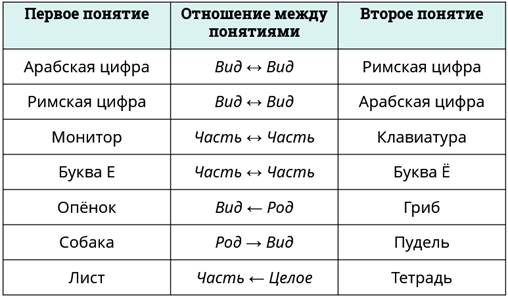
В первой паре понятий «арабская цифра», «римская цифра» отношения вид ↔ вид.
Во второй паре понятий «римская цифра», «арабская цифра» отношения вид ↔ вид. Как мы уже сказали, если понятия при симметричных отношениях поменять местами, то название отношения не изменится.
Следующая пара «монитор», «клавиатура». А вот тут надо быть внимательным. И монитор, и клавиатура – это часть от целого «компьютера». В данном случае отношение между понятиями часть ↔ часть.
В следующей паре отношение между понятиями тоже часть ↔ часть.
В этой паре отношение между понятиями вид ← род.
Между понятиями «собака», «пудель» отношение род → вид.
И последняя пара понятий «лист», «тетрадь» отношение часть ← целое.
Есть и другие виды отношений между понятиями. Например, отношение пересечения понятий.
Давайте сразу рассмотрим на примере.
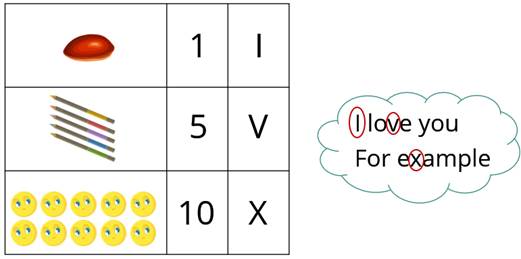
Изображён один пирожок. Обозначим количество пирожков, используя арабские цифры и римские цифры.
Вот изображено пять карандашей.
Десять смайликов также арабскими цифрами и римскими.
У меня такое ощущение, что эти римские цифры я не раз видел не в качестве цифр, а в качестве букв. Ну, да!
Смотрите, ребята, что получается, некоторые латинские буквы используются в качестве римских цифр.
Поэтому мы смело можем сказать, что понятие «буква» и понятие «цифра» находятся в отношении пересечения. Такое отношение удобно изображать наглядной схемой – кругами Эйлера.
Вот круг, который обозначает понятие «буква», а вот круг, обозначающий понятие «цифра». И эти оба круга пересекаются. А ещё они находятся внутри большого круга «знак».
Глядя на круги Эйлера, мы можем сказать, что понятия «буква» и «цифра» входят в понятие «знак».
Кругами Эйлера можно изобразить и непересекающиеся понятия. Например, понятия «компьютер» и «человек». Они не пересекаются, так как ни один компьютер не является человеком и не один человек не является компьютером в современном понимании этого слова.
Круги Эйлера – это наглядное и удобное представление отношений между двумя или несколькими понятиями. Размер кругов Эйлера может быть любым: маленьким или большим, не имеет значение. Главное, чтобы были правильно представлены отношения между понятиями. Круг, который обозначает видовое понятие, должен быть меньше и входить в другой круг большего размера, который обозначает родовое понятие.
А сейчас выполним небольшое задание.
Представьте с помощью кругов Эйлера отношения между понятиями «носитель информации», «бумага», «камень» и отношения между понятиями «двузначное число», «чётное число», «натуральное число».
В первой группе слов отношения между понятиями выглядят вот так.
Понятия «бумага» и «камень» входят в понятие «носитель информации». «Бумага» и «камень» – это непересекающиеся понятия.
Отношения между понятиями во второй группе выглядят так.
Понятия «двузначное число» и «чётное число» входят в понятие «натуральное число».
Понятие «двузначное число» и понятие «чётное число» находятся в отношении пересечения. Ведь некоторые двузначные числа являются чётными числами.
Итак, какие же итоги можно подвести из нашего урока.
Отношения между понятиями бывают род → вид, вид ↔ вид, вид ← род, целое → часть, часть ← целое и часть ↔ часть.
Отношения могут быть симметричными и несимметричными. Отношения между видовыми понятиями одного уровня (вид ↔ вид) – симметричные. Отношения между родовым и видовым понятиями (род → вид и вид ← род) – несимметричные.
Круги Эйлера помогают наглядно представить информацию об отношениях между понятиями.