Что такое внутренние углы
Углы многоугольника
Внутренний угол многоугольника — это угол, образованный двумя смежными сторонами многоугольника. Например, ∠ABC является внутренним углом.
Внешний угол многоугольника — это угол, образованный одной стороной многоугольника и продолжением другой стороны. Например, ∠LBC является внешним углом.
Количество углов многоугольника всегда равно количеству его сторон. Это относится и к внутренним углам и к внешним. Несмотря на то, что для каждой вершины многоугольника можно построить два равных внешних угла, из них всегда принимается во внимание только один. Следовательно, чтобы найти количество углов любого многоугольника, надо посчитать количество его сторон.
Сумма внутренних углов
Сумма внутренних углов выпуклого многоугольника равна произведению 180° и количеству сторон без двух.
где s — это сумма углов, 2d — два прямых угла (то есть 2 · 90 = 180°), а n — количество сторон.
Если мы проведём из вершины A многоугольника ABCDEF все возможные диагонали, то разделим его на треугольники, количество которых будет на два меньше, чем сторон многоугольника:
Следовательно, сумма углов многоугольника будет равна сумме углов всех получившихся треугольников. Так как сумма углов каждого треугольника равна 180° (2d), то сумма углов всех треугольников будет равна произведению 2d на их количество:
Из этой формулы следует, что сумма внутренних углов является постоянной величиной и зависит от количества сторон многоугольника.
Сумма внешних углов
Сумма внешних углов выпуклого многоугольника равна 360° (или 4d).
где s — это сумма внешних углов, 4d — четыре прямых угла (то есть 4 · 90 = 360°).
Сумма внешнего и внутреннего угла при каждой вершине многоугольника равна 180° (2d), так как они являются смежными углами. Например, ∠1 и ∠2:
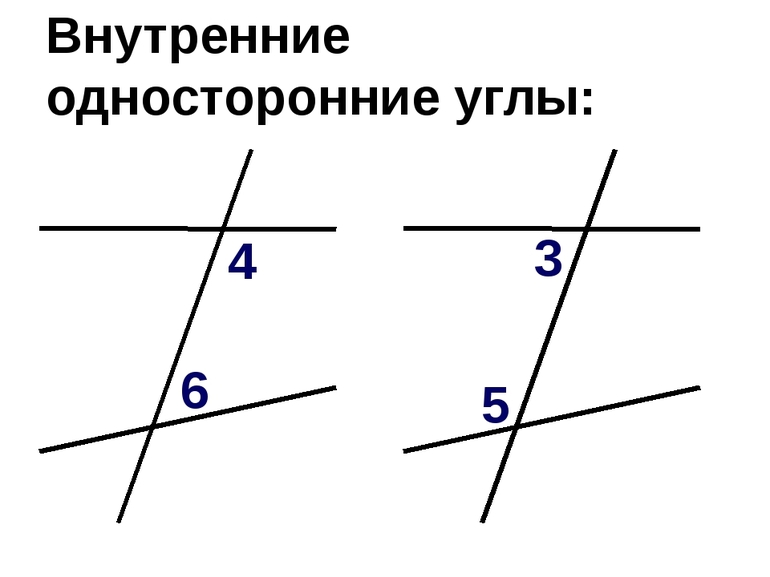
Внутренние односторонние углы
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.

∠3 и ∠4
— внутренние односторонние углы при прямых a и b и секущей c.
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.
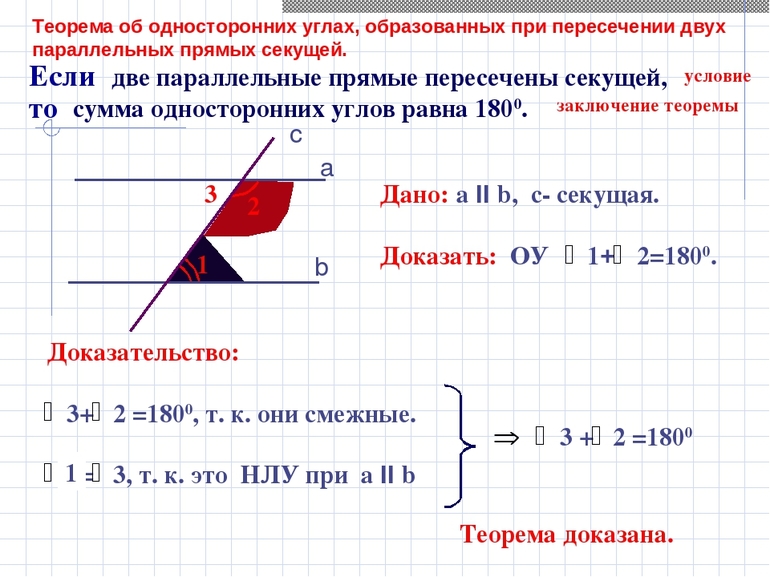
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.

∠1 + ∠2 = 180º
(как внутренние односторонние при a ∥ b и секущей c).
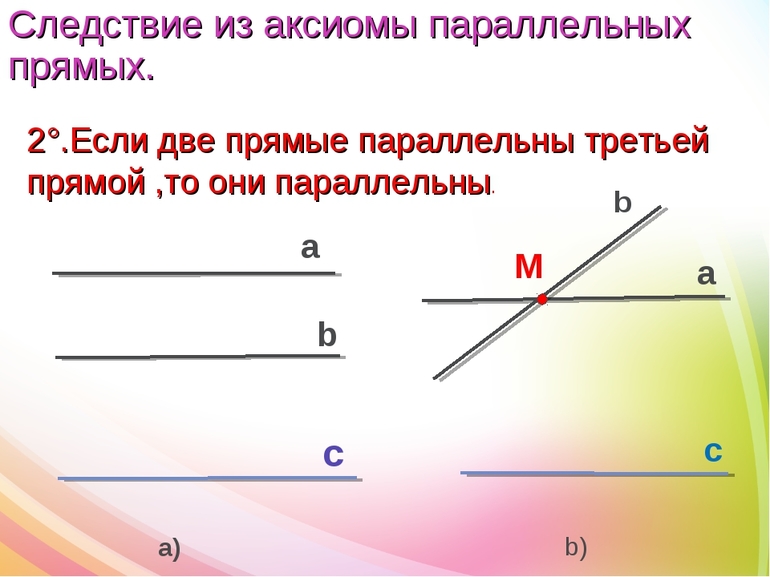
Признак параллельных прямых
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.

А так как эти углы — внутренние односторонние при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Могут ли быть внутренние односторонние углы равны?
Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.

∠1 = ∠2
тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.
Что такое внутренние углы
Определение 1. Угол − это геометрическая фигура,которая состоит из двух лучей, исходящих из одной точки.
Лучи называются сторонами угла, а их общее начало − вершиной угла.
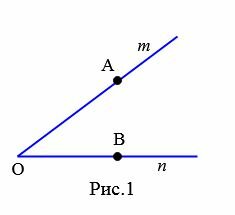 |
Обозначение угла
На рисунке 1 изображен угол с вершиной O и сторонами m и n. Данный угол обозначают \( \small ∠mn \) или \( \small ∠O. \) Если на сторонах угла выбрать точки A и B, то угол можно обозачить так: \( \small ∠AOB \) или \( \small ∠BOA. \)
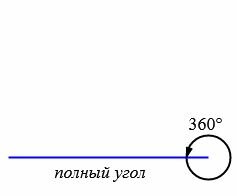
Развернутый угол. Внутренняя и внешняя область угла
Угол называется развернутым, если его стороны находятся на одной прямой. На рисунке 2 изображен развернутый угол с вершиной А и сторонами m и n.
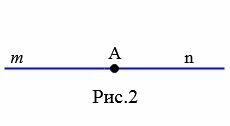 |
Любой угол разделяет плоскость на две части. Если угол неразвернутый, то меньшая из частей называется внутренней областью, а другая − внешней областью этого угла (Рис.3).
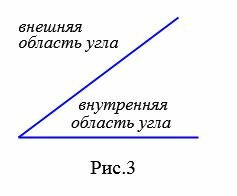 |
Если угол развернутый, то любую из двух частей, на которые разделяет угол данную плоскось можно считать внутренней областью угла.
Фигуру, состоящую из угла и его внутренней области также называют углом.
На рисунке 4 точки P и Q лежат внутри угла mn (т.е. во внутренней области угла), точки R и S лежат вне угла mn (т.е. во внешней области угла), а точки A и B на сторонах этого угла.
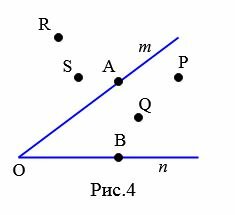 |
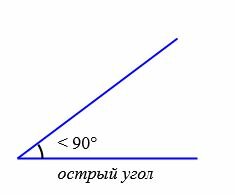
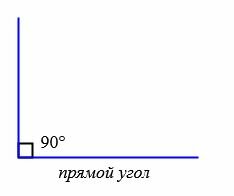
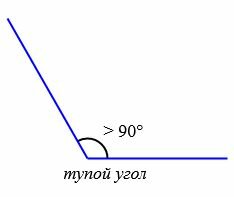
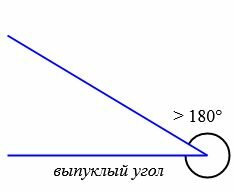
Типы углов
В зависимости от величин, углы бывают следующих типов (Рис.5):
  |
  |
  |
Сравнение углов
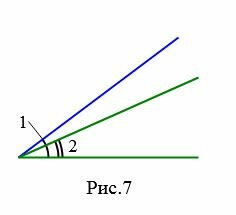
Углы можно сравнить, то есть определить равны ли они или какой угол меньше а какой больше. Чтобы определить равны ли углы или нет нужно наложить один угол на другой так, чтобы сторона одного угла совместилась со стороной другого угла а две другие оказались по одну сторону от совместившихся сторон. Если две другие стороны также совместились, то углы полностью совместятся и,следовательно они равны. Если же эти стороны не совместяться, то меньшим считается тот угол, который является частью другой.
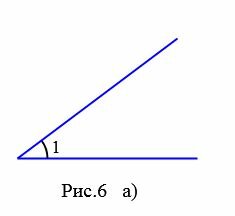 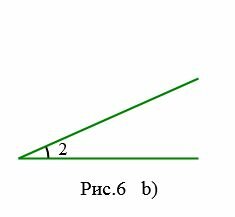 |
На рисунках 6a и 6b представлены два угла: 1 и 2. На рисунке 7 угол 2 является частью угла 1, следовательно угол 2 меньше угла 1. Это пишется так: \( \small ∠2 \lt \angle 1. \)
 |
Градусная мера угла
Измерение углов основана на сравнении их с углом, принятым за единицу измерения. За единицей измерения углов примнимают градус, которая является \( \small \frac <1> <180>\) частью развернутого угла. Положительное число, показывающая, сколько раз градус и его части помещаются в данном угле называвется градусной мерой угла. Для измерения углов используют транспортир (Рис.8).
 |
Для угла AOB, градусная мера которого равна 120° говорят «угол AOB равен 120° » и пишут: \( \small ∠AOB=120 °. \) Очевидно, что градусная мера развернутого угла равна 180°. \( \small \frac <1> <60>\) часть градуса называется минутой и обозначается так: » ‘ «. \( \small \frac <1> <60>\) часть минуты называется секундой и обозначается так: » » «. Если градусная мера угла AOB равна 56 градусов 6 минут и 43 секунды, то пишут: \( \small \angle AOB=56°6’43». \)
Отметим, что равные углы имеют равные градусные меры. Если углы разные, то меньший угол имеет меньшую градусную меру.
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
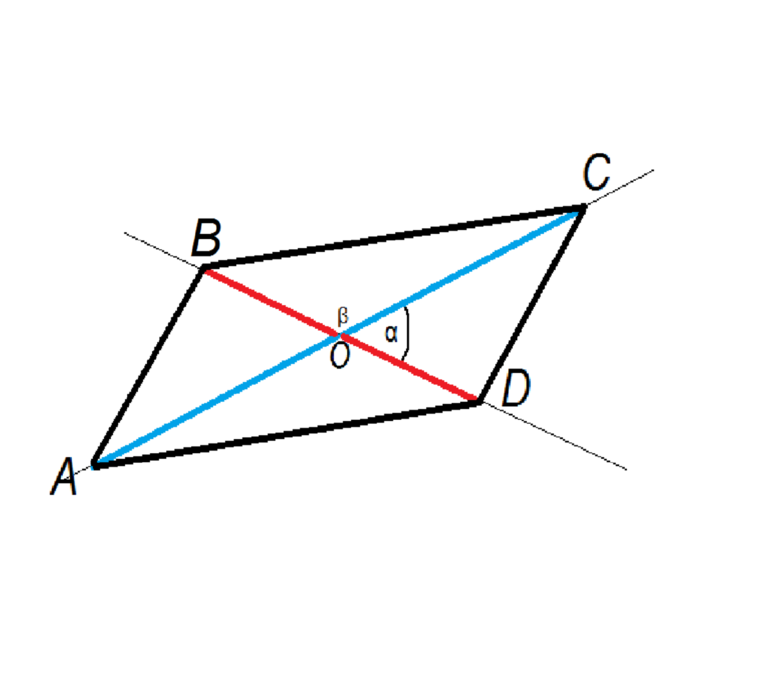
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Внутренний угол
Многоуго́льник — это геометрическая фигура, определяется как замкнутая ломаная. Существуют три различных варианта определения:
Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
| В Викисловаре есть статья « многоугольник » Многоугольники | |
| Многоугольники: | Двуугольник • Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • Девятиугольник • Десятиугольник |
|---|---|
| Правильные многоугольники: | Треугольник • Четырёхугольник • Пятиугольник • Шестиугольник • Семиугольник • Восьмиугольник • 17-угольник • 257-угольник • 65537-угольник |
Смотреть что такое «Внутренний угол» в других словарях:
Внутренний угол а — 3.6 Внутренний угол а Угол между верхней поверхностью клыка и передней поверхностью спинки Источник: ГОСТ 30013 93: Машины напольного транспорта. Плиты грузовые, вилы. Технические условия … Словарь-справочник терминов нормативно-технической документации
внутренний угол (синхронной машины) — угол выбега ротора — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы угол выбега ротора EN torque… … Справочник технического переводчика
внутренний угол конуса (торца алмазного бескернового наконечника) — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN apex angle … Справочник технического переводчика
УГОЛ — муж. перелом, излом, колено, локоть, выступ или залом (впадина) об одной грани. Угол линейный, всякие две встречные черты и промежуток их; угол плоскостной или в плоскостях, встреча двух плоскостей или стен; угол толстый, теловой, встреча в одной … Толковый словарь Даля
угол потока в абсолютном движении — Внутренний угол в треугольнике скоростей между векторами абсолютной скорости воздуха (газа) и окружной скорости лопаток. Примечание Для турбины в сечении на выходе из рабочего колеса за угол потока в абсолютном движении принимается дополнительный … Справочник технического переводчика
угол потока в относительном движении — Внутренний угол в треугольнике скоростей между векторами относительной скорости воздуха (газа) и окружной скорости лопатки. Примечание Для турбины ГТД в сечении на входе в рабочее колесо за угол потока в относительном движении принимается… … Справочник технического переводчика
Угол (Angle) — 1. В анатомии например, угол глаза (angle of the eye) внешний или внутренний угол глаза; угол рта (angle of the mouth) места соединения верхней и нижней губы. 2. Степень расходимости двух пересекающихся линий или плоскостей; пространство между… … Медицинские термины
УГОЛ — (angle) 1. В анатомии например, угол глаза (angle of the eye) внешний или внутренний угол глаза; угол рта (angle of the mouth) места соединения верхней и нижней губы. 2. Степень расходимости двух пересекающихся линий или плоскостей; пространство… … Толковый словарь по медицине
угол наклона линии зуба конического зубчатого колеса — (β) угол наклона линии зуба Ндп. угол спирали Острый угол между пересекающимися в данной точке линией зуба и образующей однотипного соосного конуса, которому принадлежит эта линия зуба. Примечания 1. Различают внешний (βe), средний… … Справочник технического переводчика
угол наклона средней линии зуба (впадины) — (βn) Острый угол между пересекающимися в данной точке средней линией зуба и образующей однотипного соосного конуса, которому принадлежит эта средняя линия зуба (впадины). Примечания 1. Различают внешний (βne), средний (βnm),… … Справочник технического переводчика