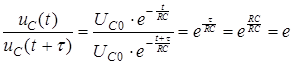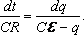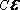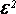Что такое время релаксации конденсатора

Зарядка конденсатора.

При полной разрядке конденсатора (при нулевом показании вольтметра, измеряющего напряжение на конденсаторе) мгновенно переключим переключатель П в положение 1 (см. рис. 1).

По второму закону Кирхгофа можно записать:

.

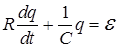
Преобразуем это уравнение к следующему виду:

. (8)

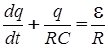
Уравнение (8) представляет собой линейное неоднородное дифференциальное уравнение 1-го порядка. Как известно из теории дифференциальных уравнений, общее решение линейного неоднородного дифференциального уравнения можно получить, прибавив любое его частное решение к общему решению соответствующего однородного уравнения.

Уравнение (5) дает общее решение однородного уравнения. Частное решение получим из условия, что конденсатор заряжается до напряжения U_C = eпри бесконечно большом времени зарядки. Поэтому

Сложив (5) и (9), получим

. (10)

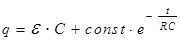
Найдем const из начального условия при t= 0, U_C=0, q=0.

, const = e × C.

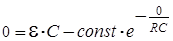
С учетом этого из (10) находим

.

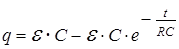
Разделив это уравнение на С, с учетом (2), запишем:

. (11)

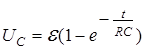
Время релаксации.

Из уравнений (6) и (11) следует, что напряжение на емкости изменяется по экспоненциальному закону. Напряжение уменьшается или возрастает тем медленнее, чем больше произведениеRC. Поэтому произведение RC называют постоянной времени и обозначают буквой t (тау).

Выясним физический смысл постоянной времени t. В соответствии с (6) можем записать

.

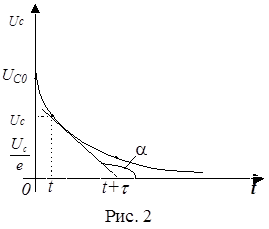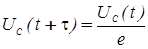
Найдем уравнение касательной графика функции (6) с учетом (12).

.

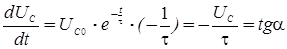
Дата добавления: 2016-04-14 ; просмотров: 1834 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Источник

ВРЕМЯ РЕЛАКСАЦИИ

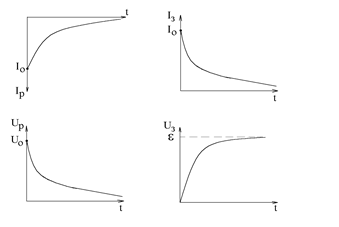
Зависимости силы тока и разности потенциалов при зарядке и разрядке конденсатора носит экспоненциальную зависимость, которая определяется величиной параметра t_теор= RC (рис.3).

Это произведение имеет размерность времени. Из дифференциальных уравнений видно, что время релаксации t есть величина обратная скорости изменения заряда на обкладках конденсатора.

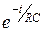
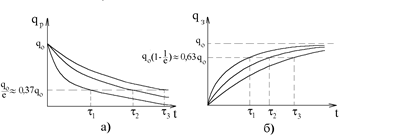
Отсюда следует, что чем больше t, тем медленнее будет уменьшаться с течением времени множитель и, следовательно, потребуется больше времени, чтобы заряд напряжения или ток достигли заданного уровня.

Таким образом, постоянная времени t характеризует длительность переходных процессов, происходящих в цепи. За время t=t заряд конденсатора либо уменьшается в e раз при разрядке конденсатора, либо достигает значения в e раз меньшего, чем максимальное q₀ при его зарядке.

Имея экспоненциальные кривые напряжения или тока, можно найти постоянную времени цепи t_эксп. Для этого на графике U(t) или I(t) при разрядке и зарядке выбирают уровень либо (рис.4а). Либо на графике U(t) при зарядке конденсатора уровень и по пересечению с графиком определяют t (рис.4б).

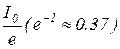
Исследование переходных процессов при зарядке и разрядке конденсаторов, построение экспоненциальных кривых, определение постоянной времени и является целью данной лабораторной работы.

Для проверки экспоненциальной зависимости и определения времени релаксации используют другой метод. Если прологарифмировать (8) и (12), то получим зависимости типа:

и (13)

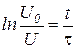
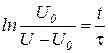
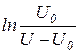
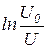
Построив графики зависимости от t или от t, получим прямые, тангенс наклона которых соответствует .

Источник

Изучение процесса заряда и разряда конденсатора

Лабораторная работа № 6

ИЗУЧЕНИЕ ПРОЦЕССА ЗАРЯДА И РАЗРЯДА КОНДЕНСАТОРА

ЦЕЛЬ РАБОТЫ

Изучение процессов заряда и разряда конденсаторов в RC-цепях, ознакомление с работой приборов, используемых в импульсной электронной технике.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ

Рассмотрим схему, пред-ставленную на рис. 1. Схема включает в себя источник постоянного тока, активное сопротивление и конденсатор, процессы заряда и разряда в котором и будем рассматривать. Эти процессы разберем по-отдельности.

Пусть вначале источник тока e подключен к конденсатору С через сопротивление R. Тогда конденсатор зарядится так, как показано на рис. 1. Переведем ключ К из положения 1 в положение 2. В результате конденсатор, заряженный до напряжения e, начнет разряжаться через сопротивление R. Считая ток положительным, когда он направлен от положительно заряженной обкладки конденсатора к отрицательно заряженной, можем записать

, , , (1)

где i – мгновенное значение силы тока в цепи, знак «минус» которого показывает, что появление тока в цепи i связано с уменьшением заряда q на конденсаторе;

q и С – мгновенные значения заряда и напряжения на конденсаторе.

Очевидно, что первые два выражения представляют собой определения силы тока и электроемкости, соответственно, а последнее – закон Ома для участка цепи.

Из двух последних соотношений выразим силу тока i следующим образом:

.

Тогда можно записать уравнение

. (2)

Это дифференциальное уравнение, решением которого является экспоненциальная функция вида

, (3)

где q0 – заряд конденсатора в начальный момент времени t=0;

– время релаксации RC-цепи, измеряемое в секундах.

Поделив обе части уравнения (3) на величину емкости С, получим

e, (4)

где e= – напряжение на конденсаторе в начальный момент времени t=0.

Зависимость напряжения на конденсаторе от времени в рассмотренном процессе показана на рис. 2.

Зная данную зависимость, можно вычислить время q, за которое напряжение на конденсаторе уменьшится в 2 раза. Подставив значение U=e/2 в уравнение (4), получим

e=e, (5)

откуда можно получить значение

. (6)

Переведем ключ К на схеме (рис. 1) из положения 2 в положение 1. В результате начнется заряд конденсатора от батареи, имеющей ЭДС e, через сопротивление R.

Уравнения, описывающие заряд конденсатора, аналогичны выражениям (1)

, e–U, q=CU. (7)

Предполагаем, что внутреннее сопротивление источника тока пренебрежимо мало по сравнению с величиной R. Теперь ток в цепи считается положительным, когда он течет в направлении положительно заряженной обкладки конденсатора. Исключая в уравнениях (7) силу тока i и напряжение на конденсаторе U, получим уравнение:

. (8)

Запишем уравнение (8) в следующем виде:

. (9)

Решая это уравнение, получим

. (10)

Коэффициент А най-дем из начальных условий, а именно, q=0 при t=0 :

Рис. 3

В результате получаем зависимость q(t):

. (11)

Поделив обе части уравнения (11) на С, получим зависимость напряжения на конденсаторе U от времени

. (12)

Зависимость U(t) показана на рис. 3. Подставив в (12) значение напряжения, равного , получим

, (13)

где q – время, за которое напряжение на конденсаторе вырастает до половины своего максимального значения ( рис. 4). Отсюда время

Следовательно, дли-тельность заряда до по-ловины максимального значения напряжения на конденсаторе будет та-кой же, как и при разряде конденсатора (см. (6)).

ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОЙ УСТАНОВКИ

Блок-схема установки представлена на рис.5.

Схема состоит из генератора прямоугольных импульсов ГИ типа Г5-54, магазина сопро-тивлений МС величиной от 0 до 10 кОм, элек-тронного осциллографа ЭО типа С1-83, и ис-следуемой емкости С.

Генератор позволяет получать прямоугольные импульсы разной длительности и амплитуды с разной частотой повторения, позволяет сдвигать время начала импульса относительно синхронизирующего импульса.

Прямоугольный импульс через магазин сопротивлений подается на исследуемый конденсатор и вход «Y» осциллографа. Осциллограф позволяет визуально следить за процессом заряда и разряда конденсатора. В работе используется емкость С»0,01 мкФ, R изменяется от 0 до 10 кОм. Для наблюдения процессов в RC–цепи удобной при этих значениях R и С является частота повторения 1–2 кГц. Длительность прямоугольного импульса должна быть достаточной для того, чтобы конден-сатор успевал зарядиться до напряжения, равного ам-плитуде импульса.

Из рис. 6 видно, что длительность прямоуголь-ного импульса Т меньше постоянной заряда RC–цепи t. Следовательно, конден-сатор не успевает зарядить-ся. Чтобы зарядить конден-сатор до напряжения, рав-ного амплитуде импульса, необходимо выполнить условие Т>>t.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Ознакомиться с блок-схемой установки, представленной на рис. 5.

2. Ознакомиться с работой генератора импульсов Г5-54, электронного осциллографа С1-83.

3. Подготовить генератор импульсов к работе, для чего выполнить следующие операции:

а) нажать кнопку «запуск»;

б) установить частоту повторения 2,0´103;

в) установить временный сдвиг 2,0´10;

г) установить длительность 2,0´10 mS;

е) нажать кнопку ´0,3;

ж) переключатель синхроимпульсов установить в положение «L»;

з) ручку «амплитуды повернуть на 1/3 вправо.

4. Подготовить осциллограф к работе, для чего:

а) ручку «развертка» поставить в позицию 10 mS;

б) нажать кнопку «0,5» внешней синхронизации;

г) вытянуть ручку «ждущая»;

д) род работы I канала установить в позицию «

е) переключатель «V/дел» поставить в положение «0,5»;

ж) нажать кнопку «I» слева от экрана.

5. Включить стенд и приборы.

6. Установить на экране осциллографа устойчивую картину, вращая ручки «развертка плавно».

7. Установить на магазине сопротивлений 1 кОм.

Упражнение 1. ОПРЕДЕЛЕНИЕ КРИВОЙ ЗАРЯДА КОНДЕН-САТОРА

1. Установить величину усиления канала Y осциллографа таким, чтобы высота импульса на экране была максимально возможной. Ввести некоторую задержку импульса, чтобы не пропало его начало. Установить частоту развертки осциллографа такой, чтобы на экране уместилась полная кривая заряда конденсатора.

2. Измерить зависимость у(х), при этом измеряя х в мкс, а у – в вольтах. Результаты занести в таблицу

3. Построить кривую заряда конденсатора.

Упражнение 2. ОПРЕДЕЛЕНИЕ КРИВОЙ РАЗРЯДА КОНДЕН-САТОРА

1. Аналогично предыдущему упражнению провести измерения для разряда конденсатора. Результаты занести в подобную таблицу.

2. По кривой разряда конденсатора определить время q. Вычислить постоянную времени t, используя формулу (6).

3. Учитывая, что погрешность определения q зависит в основном от приборной, оценить и рассчитать относительную погрешность

.

4. Аналогичные измерения провести для значений R=2 кОм и 0,5 кОм.

4. На основании полученных значений t для 3-х разных R вычислить величину емкости С. Определить относительную погрешность

,

где Dt и DR – абсолютные погрешности измерения.

5. Определить абсолютную погрешность величины емкости при данных измерениях.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое электрическая цепь, какие элементы входят в состав замкнутой электрической цепи?

2. Что такое электроемкость проводника? От каких параметров зависит величина электроемкости плоского конденсатора?

3. Оъясните понятие «RC-цепочка»?

4. Переходные процессы, в каких цепях они возможны?

5. Что означают «мгновенные значения» электрического тока и напряжения, как их вычислить?

6. Как определить максимальные значения напряжения на конденсаторе и тока в цепи?

7. Что такое постоянный электрический ток? Чем он отличается от переменного?

8. Каким образом определяется направление тока в цепи?

9. Вывести уравнение (1).

10. Что такое время релаксации?

11. Какова зависимость напряжения на конденсаторе от времени при его разрядке?

12. Вывести закон изменения напряжения на конденсаторе при зарядке конденсатора.

13. Объясните физический смысл уравнения (6).

14. Сравните время заряда и разряда конденсатора.

15. Каким условиям должна удовлетворять длительность импульса генератора?

16. Объяснить работу установки по принципиальной электрической схеме.

17. Нарисовать блок-схему установки и рассказать порядок выполнения работы.

18. Почему в данной установке нет источника постоянного тока, показанного на принципиальной схеме?

19. Можно ли в данной установке применить генератор синусоидального напряжения, пилообразного напряжения?

20. Какой частоты и длительности импульсы должен вырабатывать генератор?

21. Для чего нужно в данной схеме активное сопротивление R? Какой должна быть ее величина?

22. Какого типа конденсаторы и резисторы могут применяться в данной установке?

23. Какие значения могут иметь емкость и сопротивление в данной схеме?

24. Для чего нужна синхронизация сигнала осциллографа?

25. Каким образом добиваются оптимального вида сигнала на экране осциллографа? Какие регулировки при этом применяются?

26. Чем отличаются цепи заряда и разряда конденсатора?

27. Какие измерения нужно провести, чтобы определить емкость конденсатора в RC-цепи?

28. Как оценить погрешности измерений при работе установки?

29. Как повысить точность определения времени релаксации RC-цепи?

30. Назовите пути повышения точности определения емкости конденсатора.

Источник

Переходные процессы в цепях постоянного тока с конденсатором

ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными

РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи

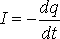
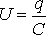
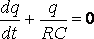
где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что и , преобразуем закон Ома к виду

(1)

В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем

, (2)

, (3)

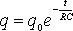
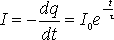
где I₀ — сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.

Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:

(4)

ЗАРЯДКА КОНДЕСАТОРА.

Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи:

.

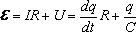
После разделения переменных уравнение примет вид:

Проинтегрировав это уравнение с учётом начального условия

q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим

, или после потенцирования

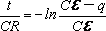
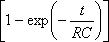
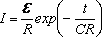
q = . (4)

. (5)

Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dА_ист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW:

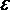
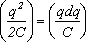
где dA_ист =Idt, dQ =I 2 Rdt, dW =d. Тогда для произвольного момента времени t имеем:

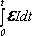
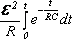
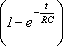
А_ист(t)===С. (6)

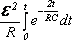
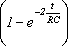
Q(t)==С. (7)

W(t) ==. (8)

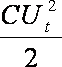
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

ЭКСПЕРИМЕНТ 1

Определение ёмкости конденсатора методом разрядки

1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.

Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), Ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).

2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.

3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.

4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.

5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I₀. Запишите это значение в таблицу 3.

6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.

7. Для каждого опыта рассчитайте I_t= I₀/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.

8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.

9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к I_t. Запишите это значение времени t₁ в таблицу 3.

10. Проделайте опыты п.п.8, 9 ещё 4 раза.

Таблица 1. Суммарное значение э.д.с. источников тока

Таблица 2. Определение сопротивления лампы.

Таблица 3. Результаты измерений и расчётов.

ОБРАБОТКА РЕЗУЛЬТАТОВ:

1. По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.

2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.

3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.

ЭКСПЕРИМЕНТ 2

Изучение зависимости от времени количества тепла, выделившегося на нагрузке при разряде конденсатора

Таблица 4. Результаты измерений и расчетов

Время разрядки t, с

Кол-во тепла Q за t с, Дж

ОБРАБОТКА РЕЗУЛЬТАТОВ:

ЭКСПЕРИМЕНТ 3

Проверка закона сохранения энергии в процессе зарядки конденсатора через сопротивление

Рис.3

Таблица 5. Результаты измерений и расчетов

ОБРАБОТКА РЕЗУЛЬТАТОВ:

Вопросы и задания для самоконтроля

Вопросы и задания для самоконтроля

Источник