Что такое выпуклая фигура

Что такое выпуклая фигура

Одним из важнейших классов тел является класс выпуклых тел. Перед тем как рассказать о нем, познакомимся с более общим понятием выпуклой фигуры.

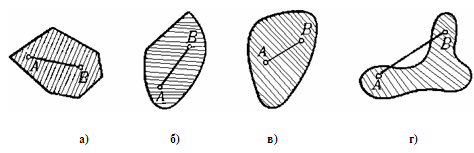
Фигура называется выпуклой, если вместе с каждыми двумя своими точками она содержит и соединяющий их отрезок (рис. 10.6).

Точка и пустое множество (фигура, не имеющая точек) считаются выпуклыми фигурами.

Примеры выпуклых фигур: отрезок, луч, прямая, плоскость, треугольник, параллелограмм, круг, все пространство, полупространство, шар (рис. 10.7). Докажем, например, что круг — выпуклая фигура.

Рассмотрим круг D радиуса R с центром О (рис. 10.8). Возьмем любые две точки . Тогда Возьмем любую точку Z на отрезке XY. Тогда выполняется хотя бы одно из двух неравенств: или (так как хотя бы один из смежных углов OZX и OZY не острый). Поскольку то и , т. е. . А это значит, что отрезок XY содержится в круге , т.е. круг D — выпуклая фигура.

Докажем несколько предложений о выпуклых фигурах. Начнем с самого важного из них.

Предложение 1. Пересечение (общая часть) любых двух выпуклых фигур есть выпуклая фигура, и вообще, пересечение любой совокупности выпуклых фигур есть выпуклая фигура.

Пусть — две выпуклые фигуры и F — их пересечение (рис. 10.9). Если две точки принадлежат фигуре F, то значит они принадлежат и фигурам . А тогда по выпуклости фигуры она содержит отрезок АВ. Аналогично, содержит отрезок АВ. Поэтому отрезок АВ содержится и в , т. е., в фигуре F. Итак, отрезок, соединяющий любые две

точки А и В фигуры F, содержится в F, т. е., фигура F — выпуклая фигура.

В случае пересечения любой совокупности выпуклых фигур доказательство то же, но следует говорить не о двух фигурах, а сразу о фигурах всей совокупности. Повторите это доказательство еще раз.

Замечание. В частности, пересечение данных фигур может быть пустым или одноточечным множеством. Если бы пустое и одноточечное множества не считались выпуклыми, то эти случаи надо было бы исключить из теоремы и ее нельзя было бы формулировать так кратко.

Предложение 1 позволяет получать выпуклые фигуры путем пересечения каких-либо выпуклых фигур. Например, треугольник ABC можно получить пересечением трех полуплоскостей, на границах которых лежат две вершины треугольника и внутри них — третья вершина (рис. 10.10). Часто используются и следующие три утверждения.

Предложение 2. Пересечение выпуклой фигуры с плоскостью является выпуклой фигурой (рис. 10.11).

Оно вытекает из предложения 1 и выпуклости плоскости.

Предложение 3. Каждая плоскость разбивает любую выпуклую фигуру на две выпуклые фигуры (рис. 10.11). Каждая из них есть пересечение исходной выпуклой фигуры с полупространством, ограниченным данной плоскостью.

Отметим, что точки исходной фигуры, лежащие в этой плоскости, относятся к каждой из полученных выпуклых фигур.

Предложение 4. Проекция выпуклой фигуры на плоскость есть выпуклая фигура.

Действительно, пусть F — выпуклая фигура и F — ее проекция на плоскость а (рис. 10.12). Возьмем любые две точки А и В фигуры F. Они являются проекциями некоторых точек А и В фигуры F. Поскольку F — выпуклая фигура, то отрезок АВ содержится в фигуре F. Значит проекция отрезка АВ — отрезок АВ — содержится в фигуре F, т. e., F— выпуклая фигура.

Отметим также, что цилиндр и конус выпуклы тогда и только тогда, когда их основания — выпуклы. Докажем это, например, для цилиндра.

Следует доказать два утверждения:

1) если цилиндр выпуклый, то его основание — выпукло;

2) если основание цилиндра выпукло, то и сам цилиндр выпуклый.

Первое утверждение непосредственно вытекает из предложения 2, так как основание цилиндра является пересечением цилиндра с плоскостью этого основания.

Докажем второе утверждение. Пусть основание F цилиндра С выпукло (рис. 10.13). Возьмем в цилиндре любые две точки А и В и проведем через них образующие и . Если А и В лежат на одной образующей, то отрезок А В лежит в цилиндре С. Поэтому будем считать, что образующие различны. Концы этих образующих, лежащие в F, — точки X и Y — являются концами отрезка XY, лежащего в F, так как основание F — выпукло.

Поэтому все отрезки , исходящие из точек Z отрезка XY, параллельные и равные отрезку , являются образующими цилиндра С. Следовательно, параллелограмм содержится в цилиндре С.

Так как отрезок АВ содержится в параллелограмме XXY Y, то отрезок А В содержится в С. Итак, цилиндр С выпуклый.

Источник

Что такое выпуклая фигура

Выпуклой называется такая фигура, которой принадлежат все точки отрезка, соединяющего любые ее две точки. Выпуклыми фигурами являются, например, круг, шар, треугольник; четырехугольники могут быть как выпуклыми, так и невыпуклыми (рис. 1).

Справедливо такое утверждение: «Общая часть двух выпуклых фигур вновь является выпуклой фигурой». Его вы сможете доказать сами, считая пустое множество выпуклой фигурой. Еще одно важное свойство плоской выпуклой фигуры: через каждую точку на ее границе можно провести прямую (она называется опорной прямой) так, что вся фигура будет лежать по одну сторону от этой прямой (рис. 2).

Верно и обратное утверждение: если через каждую точку границы некоторой плоской фигуры можно провести опорную прямую, то эта фигура является выпуклой. Таким образом, существование опорных прямых в каждой граничной точке можно принять за определение плоской выпуклой фигуры.

Для выпуклых тел опорные плоскости определяются аналогично (рис. 3).

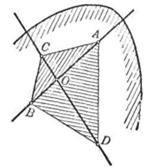
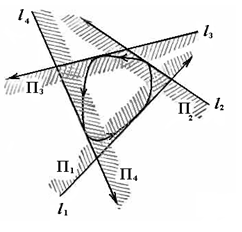
Наличие опорных прямых и плоскостей у выпуклых фигур является фактом довольно очевидным. Гораздо менее очевиден следующий факт, открытый в 1913 г. австрийским математиком Э. Хелли: «Если из нескольких заданных на плоскости выпуклых фигур каждые три имеют общую точку, то тогда существует точка, принадлежащая всем этим фигурам». Требование выпуклости в этом утверждении существенно. Действительно, на рис. 4 изображены четыре фигуры, из которых лишь одна невыпукла, однако хотя у любых трех из них есть общая точка, но нет точки, общей всем четырем фигурам.

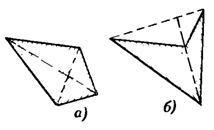
Для выпуклых тел (в пространстве) теорема Хелли в приведенном виде неверна. Чтобы в этом убедиться, достаточно рассмотреть четыре треугольника, образующих грани треугольной пирамиды. Однако если потребовать, чтобы у системы выпуклых тел в пространстве каждые четыре тела имели общую точку, то тогда и все эти тела будут иметь общую точку. Теорема Хелли в соответствующей формулировке была доказана для пространства произвольного числа измерений и в этом виде оказалась очень полезной во многих математических исследованиях.

В последнее время понятие выпуклости получило широкое распространение в математике, особенно в ее прикладных областях. Появились «выпуклый анализ» и «выпуклое программирование», результаты которых облегчают поиск решений (особенно на ЭВМ) многих важных практических задач экономики, управления и других областей. Одним из самых интересных разделов геометрической теории выпуклых фигур является теория кривых постоянной ширины. Так называют кривую, ограничивающую такую выпуклую фигуру на плоскости, для которой расстояние между каждой парой параллельных опорных прямых равно одному и тому же постоянному числу .

Простейшей кривой постоянной ширины является окружность, но трудно представить себе другую кривую с таким свойством. Первым такую кривую нашел не математик, а французский механик Ф. Рело. Это равносторонний криволинейный треугольник, стороны которого являются дугами окружностей с центрами в вершинах этого треугольника (рис. 5). Из рис. 6 нетрудно понять способы построения двух других кривых постоянной ширины. Интересно, что длина любой кривой постоянной ширины равна .

Кривые постоянной ширины имеют многочисленные практические применения. На рис. 7 изображен механизм, состоящий из подвижной рамки, способной подниматься и опускаться, и треугольника Рело, который может вращаться вокруг своей вершины . При таком вращении рамки часть периода полного оборота находится в нижнем положении, потом периода поднимается вверх, далее неподвижно стоит там еще периода и за последние периода опускается вниз. Такое движение часто бывает необходимым, например, в киносъемочных аппаратах и кинопроекторах.

Треугольник Рело, как и любая кривая постоянной ширины , может вращаться внутри полосы ширины , как в описанном механизме, постоянно касаясь обеих прямых, более того, он может вращаться внутри квадрата со стороной , касаясь одновременно всех четырех его сторон.

А существуют ли такие выпуклые фигуры, которые могут вращаться внутри, скажем, равностороннего треугольника, постоянно касаясь всех его сторон? Одну такую фигуру вы знаете – это вписанный круг. А еще? Оказывается, таким свойством обладает пересечение двух кругов одинакового радиуса, расположенных так, что центр каждого из них лежит на границе другого (рис. 8). В отличие от круга, который при вращении продолжает касаться каждой прямой в одной и той же точке, этот двуугольник при вращении входит в соприкосновение последовательно и со всеми точками границы треугольника. Это его свойство позволило сконструировать механизм, позволяющий высверливать отверстия треугольной формы.

Источник

Что такое выпуклая фигура

Выпуклой называется такая фигура, которой принадлежат все точки отрезка, соединяющего любые ее две точки. Выпуклыми фигурами являются, например, круг, шар, треугольник; четырехугольники могут быть как выпуклыми, так и невыпуклыми (рис. 1).

Справедливо такое утверждение: «Общая часть двух выпуклых фигур вновь является выпуклой фигурой». Его вы сможете доказать сами, считая пустое множество выпуклой фигурой. Еще одно важное свойство плоской выпуклой фигуры: через каждую точку на ее границе можно провести прямую (она называется опорной прямой) так, что вся фигура будет лежать по одну сторону от этой прямой (рис. 2).

Верно и обратное утверждение: если через каждую точку границы некоторой плоской фигуры можно провести опорную прямую, то эта фигура является выпуклой. Таким образом, существование опорных прямых можно принять за определение плоской выпуклой фигуры.

Для выпуклых тел опорные плоскости определяются аналогично (рис. 3).

Наличие опорных прямых и плоскостей у выпуклых фигур является фактом довольно очевидным. Гораздо менее очевиден следующий факт, открытый в 1913г. австрийским математиком Э. Хелли: «Если из нескольких заданных на плоскости выпуклых фигур каждые три имеют общую точку, то тогда существует точка, принадлежащая всем этим фигурам». Требование выпуклости в этом утверждении существенно. Действительно, на рис. 4

изображены четыре фигуры, из которых лишь одна невыпукла, однако хотя у любых трех из них есть общая точка, но нет точки, общей всем четырем фигурам. Для выпуклых тел (в пространстве) теорема Хелли в приведенном виде неверна. Чтобы в этом убедиться, достаточно рассмотреть четыре треугольника, образующих грани треугольной пирамиды. Однако если потребовать, чтобы у системы выпуклых тел в пространстве каждые четыре тела имели общую точку, то тогда и все эти тела будут иметь общую точку. Теорема Хелли в соответствующей формулировке была доказана для пространства произвольного числа измерений и в этом виде оказалась очень полезной во многих математических исследованиях.

В последнее время понятие выпуклости получило широкое распространение в математике, особенно в ее прикладных областях. Появились «выпуклый анализ» и «выпуклое программирование». результаты которых облегчают поиск решений (особенно на ЭВМ) многих важных практических задач экономики, управления и других областей. Одним из самых интересных разделов геометрической теории выпуклых фигур является теория кривых постоянной ширины. Так называют кривую, ограничивающую такую выпуклую фигуру на плоскости, для которой расстояние между каждой парой параллельных опорных прямых равно одному и тому же постоянному числу h.

Простейшей кривой постоянной ширины является окружность, но трудно представить себе другую кривую с таким свойством. Первым такую кривую нашел не математик, а французский механик Ф. Рело. Это равносторонний криволинейный треугольник, стороны которого являются дугами окружностей с центрами в вершинах этого треугольника (рис. 5). Из рис. 6

,

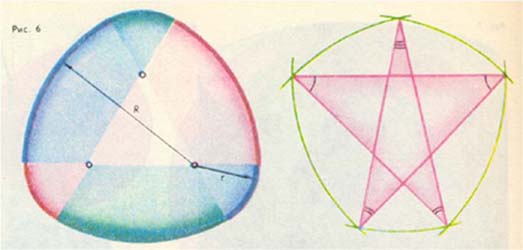
нетрудно понять способы построения двух других кривых постоянной ширины. Интересно, что длина любой кривой постоянной ширины h равна πh.

Кривые постоянной ширины имеют многочисленные практические применения. На рис. 7

изображен механизм, состоящий из подвижной рамки, способной подниматься и опускаться, и треугольника Рело, который может вращаться вокруг своей вершины О. При таком вращении рамки 1/6 часть периода полного оборота находится в нижнем положении, потом 1/3 периода поднимается вверх, далее неподвижно стоит там еще 1/6 периода и за последние 1/3 периода опускается вниз. Такое движение часто бывает необходимым, например, в киносъемочных аппаратах и кинопроекторах.

Треугольник Рело как и любая кривая постоянной ширины h, может вращаться внутри полосы ширины h, как в описанном механизме, постоянно касаясь обеих прямых, более того, он может вращаться внутри квадрата со стороной h, касаясь одновременно всех четырех его сторон.

В отличие от круга, который при вращении продолжает касаться каждой прямой в одной и той же точке, этот двуугольник при вращении входит в соприкосновение последовательно и со всеми точками границы треугольника. Это его свойство позволило сконструировать механизм, позволяющий высверлить отверстия треугольной формы.

Источник

Общие свойства выпуклых фигур

1. Общие свойства выпуклых фигур

Определение 1.1.1. Плоская фигура называется выпуклой, если она целиком содержит прямолинейный отрезок, соединяющий любые две принадлежащие фигуре точки.

Так, на рис. 1.1.1 фигуры а), б), в) выпуклые фигуры, а фигура на рисунке 1.1.1 г) не выпукла. Круг и треугольник являются выпуклыми фигурами, четырехугольник же может быть как выпуклым, так и невыпуклым в зависимости от того, пересекаются ли его диагонали внутри или вне четырехугольника (рис. 1.1.2 а, б). [1, 38]

Определение 1.1.2. Пересечением двух (или нескольких) фигур называется фигура, состоящая из всех точек, принадлежащих обеим (или всем, если их несколько) фигурам.

Определение 1.1.3. Фигура называется ограниченной, если она целиком помещается внутри некоторой окружности. [8, 13]

Например, всякий параллелограмм, треугольник, круг, а также все фигуры, изображенные на рис. 1.1.1, являются ограниченными фигурами.

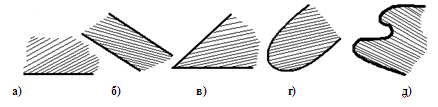
На рис. 1.1.3 изображено несколько неограниченных фигур; из них выпуклыми являются фигуры а) (полуплоскость), б) (полоса), в) (угол) и г).

По отношению ко всякой плоской фигуре все точки плоскости делятся на три категории: внутренние, внешние и граничные. [8, 14]

Определение 1.1.4. Точка фигуры называется внутренней, если существует круг (хотя бы очень малого радиуса) с центром в этой точке, целиком принадлежащий фигуре.

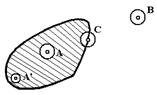
Внутренними точками фигуры будут, например, точки А и А’ на рис. 1.1.4.

Определение 1.1.5. Точка называется внешней по отношению к фигуре, если существует круг с центром в этой точке, не содержащий точек фигуры.

Примером внешней точки по отношению к фигуре является точка В на рис. 1.1.4.

Определение 1.1.6. Точка фигуры называется граничной, если любой круг с центром в данной точке, всегда будет содержать как точки, принадлежащие фигуре, так и точки, не принадлежащие ей.

Например, точка С на рис. 1.1.4 является примером граничной точки фигуры. [7, 185]

Граничные точки фигуры образуют некоторую линию — кривую или ломаную. Эта линия называется границей фигуры. Если плоская линия является границей некоторой выпуклой фигуры, то она называется выпуклой кривой, или — в том случае, когда эта линия ломаная,— выпуклым многоугольником. [7, 186]

Определение 1.1.7. Выпуклым многоугольником называют и плоскую фигуру, и линию — границу этой фигуры.

Определение 1.1.8. Точками, принадлежащими фигуре, или, точками фигуры, называют все ее внутренние или граничные точки.

Определение 1.1.9. Если множество содержит все свои граничные точки, то оно называется замкнутым. Если же множество не содержит ни одной своей граничной точки, т.е. состоит из одних внутренних точек, то оно называется открытым. [7, 15]

Определение 1.1.10. Одномерные выпуклые фигуры это линии, обладающие тем свойством, что отрезок АВ, соединяющий любые две точки А и В такой линии, целиком принадлежит ей. [8, 16]

Одномерные выпуклые фигуры можно охарактеризовать как выпуклые фигуры, все точки которых являются граничными.

Двумерные (плоские) выпуклые фигуры могут быть весьма разнообразны (см., например, фигуры а), б), в) на рис. 1.1.1 и а), б), в), г) на рис. 1.1.3).

Определение 1.1.11. Отрезок это ограниченная одномерная выпуклая фигура.

Пусть Ф — произвольная плоская фигура.

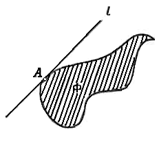
Определение 1.1.12. Прямая l называется опорной прямой фигуры Ф, если она проходит хотя бы через одну граничную точку фигуры Ф и вся фигура Ф расположена по одну сторону от прямой l (рис. 1.1.5).

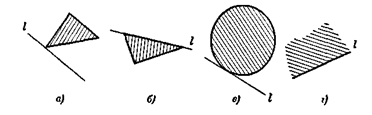
Например, прямая, проведенная через вершину треугольника параллельно противолежащей стороне (рис. 1.1.6, а), или сторона треугольника (рис. 1.1.6, 6) являются опорными прямыми треугольника; каждая сторона выпуклого многоугольника является его опорной прямой. Касательная к окружности является опорной прямой для круга, ограниченного этой окружностью (рис. 1.1.6, в). Опорная прямая может иметь с выпуклой ограниченной фигурой или единственную общую точку (см., например, рис. 1.1.6, а, в), или целый общий отрезок (рис. 1.1.6, б); если выпуклая фигура не ограничена, то опорная прямая может даже целиком принадлежать фигуре (рис. 1.1.6, г). [8, 18]

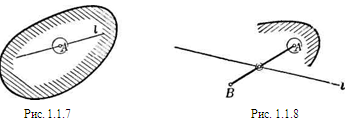
Опорную прямую выпуклой фигуры Ф можно также определить следующим образом:

Действительно, прежде всего ясно, что опорная прямая не может содержать внутренней точки А фигуры: в противном случае точки фигуры Ф, расположенные внутри некоторой окружности с центром в точке А, находились бы по обе стороны от опорной прямой (рис. 1.1.7). С другой стороны, если прямая l не содержит внутренних точек выпуклой фигуры Ф, то вся фигура должна быть расположена по одну сторону от l. Действительно, пусть А — какая-нибудь внутренняя точка Ф. Если бы какая-либо (внутренняя или граничная) точка В фигуры находилась по другую сторону от прямой l, чем точка А (рис. 1.1.8), то точка пересечения прямой l с отрезком АВ была бы внутренней точкой Ф (см. задачу 1.1.3 а, б). [8, 19]

Теорема 1.1.1. К каждой ограниченной выпуклой фигуре можно провести в точности две опорные прямые, параллельные данному направлению.

Для того чтобы это доказать, проведем через каждую точку ограниченной выпуклой фигуры Ф прямую, параллельную данному направлению (рис. 1.1.9). Все эти прямые пересекают произвольную прямую, перпендикулярную к выбранному направлению, по одномерной выпуклой фигуре (если А и В — две произвольные точки пересечения нашей совокупности прямых с перпендикулярной к ним прямой, а С—произвольная точка отрезка АВ, то С тоже должна принадлежать этому пересечению; это нетрудно видеть из рис. 1.1.9, если воспользоваться выпуклостью фигуры Ф). Следовательно, это пересечение должно быть отрезком прямой линии (ограниченность пересечения вытекает из ограниченности фигуры Ф), а совокупность прямых, параллельных заданному направлению, проведенных через все точки Ф, должна представлять собой полосу. Крайние (граничные) прямые l₁ и l₂ этой полосы и являются двумя опорными прямыми, параллельными заданному направлению.

Теорема доказана. [8, 20]

Определение 1.1.14. Наибольшее расстояние между двумя точками плоской фигуры Ф называется диаметром фигуры.

Иначе говоря, диаметром фигуры Ф называется такое расстояние d, что, во-первых, расстояние между любыми двумя точками М и N фигуры Ф не превосходит d и, во-вторых, можно отыскать в фигуре Ф хотя бы одну пару точек А и В, расстояние между которыми в точности равно d. [1, 6]

Например, для круга диаметр, в указанном смысле, совпадает с обычным его диаметром (наибольшая из хорд).

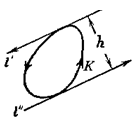
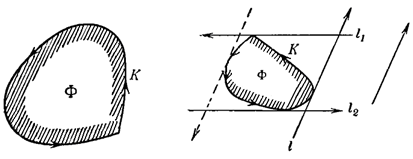
Определение 1.1.15. Пусть К выпуклая кривая l’ и l’’ две ее параллельные опорные прямые. Расстояние h между этими опорными прямыми называется шириной кривой К в направлении перпендикулярном к прямым l’ и l’’ (рис. 1.1.10). [7, 198]

Определение 1.1.16. Наименьшую ширину выпуклой кривой К называют шириной К.

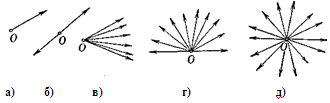
Определение 1.1.17. Совокупность лучей, исходящих из одной точки О, называется выпуклой, если она содержит все лучи, проходящие внутри угла, меньшего 180°, образованного любыми двумя лучами совокупности, не составляющими продолжение один другого.

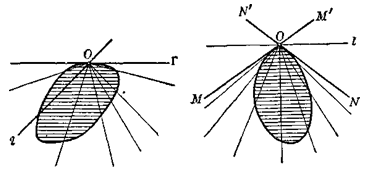
Теорема 1.1.2. Выпуклая совокупность лучей может быть одним лучом, парой лучей, являющихся продолжением один другого, углом, меньшим 180°, полуплоскостью либо целой плоскостью (рис. 1.1.11).

В самом деле, из определения выпуклой совокупности лучей непосредственно следует, что пересечение такой совокупности с любой прямой, не проходящей через точку О, выпукло. Рассматривая пересечения выпуклой совокупности лучей, с двумя параллельными прямыми, расположенными по разные стороны от точки О, и учитывая, что каждое из этих пересечений может совсем не содержать точек, быть единственной точкой, отрезком, лучом или всей прямой, нетрудно выяснить, что выпуклая совокупность лучей может быть только одного из перечисленных выше видов; все возможные здесь случаи приведены на рис. 1.1.12. [8, 21]

Теорема доказана. [8, 22]

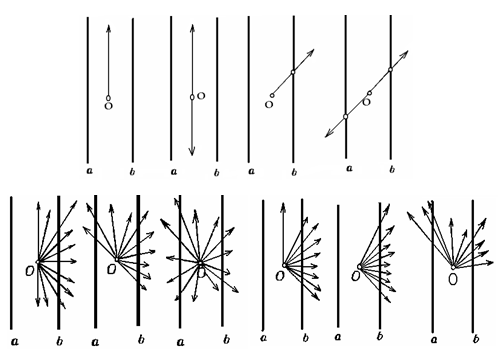
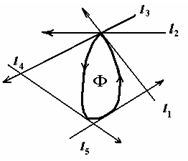
Пусть Ф — некоторая выпуклая фигура и О — ее граничная точка. Проведем из точки О лучи, соединяющие ее с каждой точкой (внутренней или граничной) фигуры Ф (рис. 1.1.13).

Мы получим выпуклую совокупность лучей. В самом деле, если ОА и ОВ — два луча данной совокупности (А и В — точки фигуры Ф), то все лучи, расположенные внутри острого угла АОВ, пересекают отрезок АВ, целиком состоящий из точек фигуры Ф, и, следовательно, принадлежат данной совокупности. [8, 22]

Получившаяся совокупность лучей не может быть единственным лучом или парой лучей, составляющих продолжение один другого, так как считается, что фигура не одномерна.

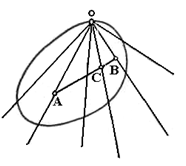
Нетрудно так же показать, что эта совокупность лучей не может заполнить всю плоскость. Действительно, если лучи заполняют плоскость, то среди них можно выбрать две такие пары лучей ОА и ОВ, ОС и ОD, что лучи каждой пары, составляют продолжение один другого. Пусть А, В, С, D—точки выпуклой фигуры, лежащие на этих лучах (рис. 1.1.14). Фигура Ф вместе с точками А, В, С должна содержать весь треугольник АВС (см. рис. 1.1.14) и вместе с точками А, В, D—весь треугольник АВD, т. е. она должна содержать весь выпуклый четырехугольник АСВD, для которого точка О является внутренней. Таким образом, в этом случае точка О не может быть граничной точкой фигуры Ф. [8, 23]

Следовательно, рассматриваемая совокупность лучей будет либо полуплоскостью, либо углом, меньшим 180°. В первом случае (рис. 1.1.15) точка О называется обыкновенной точкой выпуклой кривой К, ограничивающей фигуру Ф.

Прямая Г, ограничивающая полуплоскость, является опорной прямой фигуры Ф (все точки Ф лежат на лучах нашей совокупности, а следовательно, с одной стороны от прямой Г).

При этом прямая Г является единственной опорной прямой фигуры Ф в точке О, так как по обе стороны от каждой другой прямой l, проходящей через О, есть лучи нашей совокупности, а следовательно, и точки фигуры Ф (рис. 1.1.15). Такая опорная прямая Г фигуры Ф, ограничивающая полуплоскость, называется касательной в точке О к выпуклой кривой К. [7, 188]

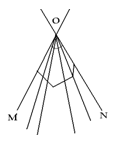
Во втором случае, когда выпуклая совокупность лучей является углом, меньшим 180°, точка О называется угловой точкой выпуклой кривой К, ограничивающей фигуру Ф (рис. 1.1.16).

Все точки фигуры Ф заключены в этом случае внутри угла МОN; поэтому всякая прямая l, проходящая внутри угла МОN’, смежного с углом МОN, будет опорной прямой фигуры Ф. В частности, опорными будут и лучи ОМ, ОN, которые называются полукасательным в точке О к выпуклой кривой К, ограничивающей фигуру Ф. [1, 40]

Согласно этому определению все точки выпуклого многоугольника, кроме вершин, являются обыкновенными, причем касательными в этих точках являются стороны многоугольника. Вершины выпуклого многоугольника являются его угловыми точками, а определенные выше углы совпадают с углами многоугольника в обычном смысле (рис. 1.1.17).

Сопоставляя оба случая — случай обыкновенной точки выпуклой кривой и случай угловой точки, приходим к заключению, что через каждую точку выпуклой кривой проходит, по крайней мере, одна опорная прямая. [1, 41]

Определение 1.1.19. Ограниченная фигура называется выпуклой, если через каждую ее граничную точку проходит, по крайней мере, одна опорная прямая. [8, 26]

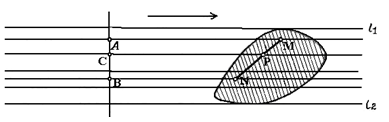
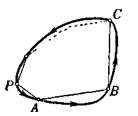
Пусть Ф — произвольная ограниченная выпуклая фигура, К— ее граница. Установим на кривой К определенное направление обхода, например, против часовой стрелки. При движении по кривой К в этом направлении фигура Ф все время остается слева (рис. 1.1.18). В соответствии с этим установим направления и на опорных прямых фигуры Ф.

Будем выбирать направление опорной прямой l фигуры Ф таким образом, чтобы фигура Ф лежала слева от прямой l (рис. 1.1.19).

В таком случае две параллельные между собой опорные прямые l₁ и l₂ фигуры Ф получат противоположные направления. Таким образом, каждому направлению в плоскости (которое можно задавать при помощи прямой со стрелкой) будет соответствовать единственная опорная прямая, имеющая это направление (рис. 1.1.19).

Если К это многоугольник, то задание направления обхода позволяет говорить о направлениях сторон многоугольника.

Может, однако, оказаться, что три (или больше) из взятых п опорных прямых будут проходить через одну и ту же граничную точку фигуры Ф (которая в этом случае обязательно является угловой; рис. 1.1.22). В таком случае описанный многоугольник будет иметь меньше чем п сторон. Такой многоугольник называют n-угольником, имеющим одну или несколько сторон нулевой длины, т. е сторон, превратившихся в точки. Эти стороны нулевой длины имеют определенные направления, а именно направления соответствующих опорных прямых

Это позволяет говорить об п внутренних и внешних углах описанного n-угольника независимо от того, имеет ли он стороны нулевой длины или нет.

Определение 1.1.23. Длиной ограниченной выпуклой кривой К и площадью фигуры Ф, которую эта кривая ограничивает, называются пределы периметров, соответственно площадей, вписанных в Ф многоугольников, все стороны которых безгранично уменьшаются, или описанных вокруг Ф многоугольников, все внешние углы которых безгранично уменьшаются.

Из этого определения следует, что если выпуклая кривая К целиком заключена внутри выпуклой кривой К’, то длина К не может быть больше длины К’.

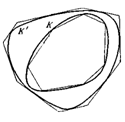
Теорема 1.1.3. Если выпуклая кривая К целиком заключена внутри выпуклой кривой К’, то длина К не может быть больше длины К’.

Действительно, рассмотрим последовательность многоугольников, вписанных в кривую К, стороны которых безгранично уменьшаются, и последовательность многоугольников, описанных вокруг К’, внешние углы которых безгранично уменьшаются (рис. 1.1.23).

Каждый из многоугольников второй последовательности заключает в себе каждый из выпуклых многоугольников первой последовательности и, следовательно, имеет больший периметр; отсюда следует, что предел периметров многоугольников второй последовательности — длина К’ не меньше предела периметров многоугольников первой последовательности — длины К.

Определение 1.1.24. Периметром плоской фигуры называется длина кривой, ограничивающей эту фигуру. [8, 28]

Источник