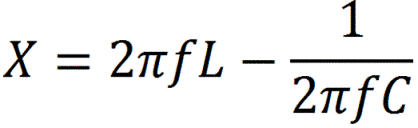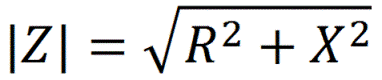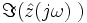Что такое высокоимпедансное состояние электрической цепи
Высокоимпедансное состояние
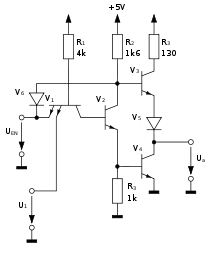
Высокоимпедансное состояние или Z-состояние — такое состояние контакта логической схемы, при котором сопротивление между этим контактом и остальной схемой очень велико. Физически реализуется закрытым транзистором, работающим в ключевом режиме.
Вывод, переведённый в Z-состояние, ведёт себя как не подключенный к схеме. Внешние устройства, подключенные к этому выводу, могут изменять напряжение на нём по своему усмотрению (в некоторых рамках), не влияя на работу схемы. И наоборот — схема не мешает внешним устройствам менять напряжение на контакте.
Потребность
В цифровой электронике существуют понятия «логическая единица» (контакт присоединён к источнику питания и может выдавать в нагрузку большой ток, порядка сотен миллиампер) и «логический ноль» (контакт присоединён к «земле», и также выдерживает высокие токи). Но такие выходы нельзя объединять: если на одном будет 1, а на другом 0, возникает короткое замыкание, чреватое выгоранием выходных транзисторов.
Поэтому, чтобы можно было организовывать соединение типа «шина», было введено третье «высокоимпедансное состояние», когда дополнительный ключ просто отключает выход и он «повисает в воздухе» — соединяется с остальной схемой через высокое сопротивление (импеданс) закрытого транзистора. Такой выход не влияет на подключённый к нему провод, следовательно к одному проводу можно подключать несколько выходов, нужно только следить, чтобы в каждый момент времени только один был активным, а остальные в высокоимпедансном состоянии. Получается соединение типа «шина».
Близкими свойствами обладает выход «открытый коллектор», но он имеет ряд недостатков, например требует применения подтягивающего резистора, который уменьшает крутизну фронта импульса.
Применение
Z-состояние применяется, когда устройству приходится временно отключаться от шины — например, в программаторах, мультиплексорах, многоточечных интерфейсах передачи данных наподобие JTAG, I2C или USB, и т. д.
Например: если интерфейс SPI настроен как подчинённый, он будет находиться в состоянии ожидания до тех пор, пока на выводе SS будет присутствовать высокий уровень, при этом линия MISO будет находиться в высокоимпедансном состоянии.
Что такое электрический импеданс
В цепях постоянного тока активное сопротивление R играет важную роль. Что касается цепей синусоидального переменного тока, то здесь не обойтись одним лишь активным сопротивлением. Ведь если в цепях постоянного тока емкости и индуктивности заметны только при переходных процессах, то в цепях переменного тока данные компоненты проявляют себя гораздо более значительно.
Представление об импедансе позволяет применять закон Ома к участкам цепей переменного синусоидального тока. Проявление двухполюсником (нагрузкой) индуктивной составляющей приводит к отставанию тока от напряжения на данной частоте, а проявление емкостной составляющей — к отставанию напряжения от тока. Активная же составляющая не вызывает задержки между током и напряжением, проявляя себя по сути так же, как и в цепи постоянного тока.
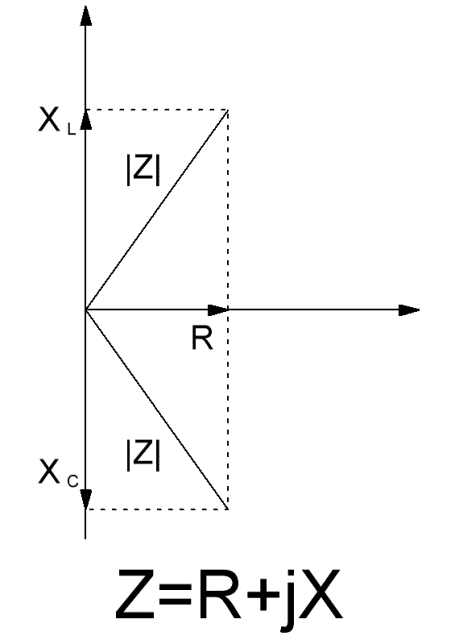
Составляющая импеданса, содержащая емкостной и индуктивный компоненты, называется реактивной составляющей X. Графически активную составляющую R импеданса можно отложить по оси оX, а реактивную — по оси оY, тогда импеданс в целом представится в форме комплексного числа, где j-мнимая единица (мнимая единица в квадрате равна минус 1).
В данном случае наглядно видно, что реактивная составляющая X может быть разложена на емкостную и индуктивную составляющие, которые имеют противоположное направление, то есть оказывают противоположное влияние на фазу тока: при преобладании индуктивной составляющей, импеданс цепи окажется в целом положительным, то есть в цепи ток будет отставать от напряжения, если же станет преобладать емкостной компонент, то напряжение будет отставать от тока.
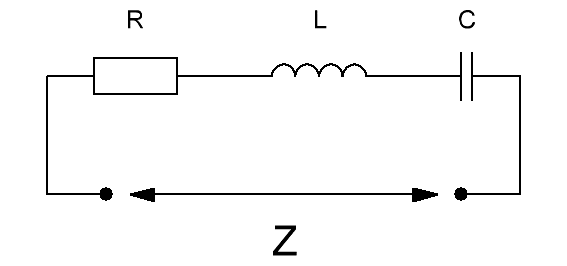
Схематически этот двухполюсник в приведенном виде изображается так:
Принципиально любая схема линейного двухполюсника может быть приведена к аналогичному виду. Здесь можно определить активную составляющую R, которая от частоты тока не зависит, и реактивную составляющую X, включающую в себя емкостную и индуктивную составляющие.
Из графической модели, где сопротивления представлены векторами, ясно, что модуль импеданса для заданной частоты синусоидального тока вычисляется как длина вектора, представляющего собой сумму векторов X и R. Измеряется импеданс в Омах.
Практически в описаниях цепей синусоидального переменного тока с точки зрения импеданса, можно встретить такие термины, как «активно-индуктивный характер нагрузки» или «активно-емкостная нагрузка» или «чисто активная нагрузка». Имеется ввиду следующее:
Если в цепи преобладает влияние индуктивности L, значит реактивная составляющая X положительна, при этом активная составляющая R мала — это индуктивная нагрузка. Пример индуктивной нагрузки — катушка индуктивности.
Если в цепи преобладает влияние емкости C, значит реактивная составляющая X отрицательна, при этом активная составляющая R мала — это емкостная нагрузка. Пример емкостной нагрузки — конденсатор.
Если в цепи преобладает активное сопротивление R, при этом реактивная составляющая X мала — это активная нагрузка. Пример активной нагрузки — лампа накаливания.
Если в цепи активная составляющая R значительна, но индуктивная составляющая преобладает над емкостной, то есть реактивная составляющая X положительна, нагрузку называют активно-индуктивной. Пример активно-индуктивной нагрузки — асинхронный двигатель.
Если в цепи активная R составляющая значительна, при этом емкостная составляющая преобладает над индуктивной, то есть реактивная составляющая X отрицательна, нагрузку называют активно-емкостной. Пример активно-емкостной нагрузки — блок питания люминесцентной лампы.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Импеданс
Импеданс
| Классическая электродинамика | ||||||||||||
 | ||||||||||||
| Магнитное поле соленоида | ||||||||||||
Электричество · Магнетизм
|
Электри́ческий импеда́нс — комплексное сопротивление двухполюсника для гармонического сигнала. Это понятие ввёл физик и математик О. Хевисайд.
Содержание
Аналогия с сопротивлением
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения и тока на нём, попытка применения термина электрическое сопротивление к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.
Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некоей стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название электрический импеданс (или просто импеданс). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.
Определение
Импедансом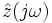 
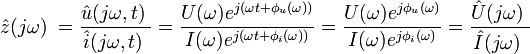называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит для данного двухполюсника понятие импеданса не применимо.
 | (1) |
Физический смысл
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом можно рассматривать как последовательно соединенные резистор с сопротивлением 
и чисто реактивный элемент с импедансом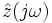 
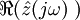
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько ток отстаёт от напряжения.
Ограничения
Понятие импеданса применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель e jωt в (1) не сокращается. Однако, импеданс зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для нее.
Электрический импеданс
 Классическая электродинамика | ||||||||||||
 | ||||||||||||
| Электричество · Магнетизм | ||||||||||||
| ||||||||||||
| См. также: Портал:Физика |
Электри́ческий импеда́нс (комплексное сопротивление, полное сопротивление) — комплексное сопротивление двухполюсника для гармонического сигнала. Это понятие ввёл физик и математик О. Хевисайд в 1886 году. [1] [2]
Содержание
Аналогия с сопротивлением
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения к току на нём, попытка применения термина электрическое сопротивление к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.
Сопротивление правильно описывает свойства катушки и конденсатора только на постоянном токе. В случае же переменного тока свойства реактивных элементов существенно иные: напряжение на катушке индуктивности и ток через конденсатор не равны нулю. Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению. Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некоей стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название электрический импеданс (или просто импеданс). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.
Определение
Импедансом 
называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник. При этом импеданс не должен зависеть от времени: если время t в выражении для импеданса не сокращается, значит, для данного двухполюсника понятие импеданса неприменимо.
 | (1) |
Исторически сложилось, что обозначение импеданса, комплексных амплитуд и других комплекснозначных функций частоты записывают как 
, а не 
. Такое обозначение показывает, что мы имеем дело с комплексными представлениями гармонических функций вида 
. Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: 
чтобы отличать от соответствующих действительных (некомплексных) величин.
Физический смысл
Навстречу нарастающему току генератора, идет ток самоиндукции катушки. Вот это противодействие тока самоиндукции катушки нарастающему току генератора, и называется индуктивным сопротивлением.На преодоление этого противодействия затрачивается часть энергии переменного тока генератора. Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки, также, будет убывать, пресекая катушку и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора. Таким образом вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, т. е. не вызывающим безвозвратных потерь энергии.
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом можно рассматривать как последовательно соединенные резистор с сопротивлением 
и чисто реактивный элемент с импедансом 
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько ток отстаёт от напряжения.
Ограничения
Понятие импеданса применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его свойства не менялись со временем. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса, не зависящее от времени t, поскольку при вычислении импеданса множитель в (1) не сокращается.
Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для нее.
Вычисление импеданса
Идеальные элементы
Резистор
Для резистора импеданс всегда равен его сопротивлению R и не зависит от частоты:
 | (2) |
Конденсатор
Ток и напряжение для конденсатора связаны соотношением:
 | (3) |
Отсюда следует, что при напряжении
 | (4) |
ток, текущий через конденсатор, будет равен:
 | (5) |
После подстановки (4) и (5) в (1) получаем:
 | (6) |
Катушка индуктивности
Аналогичное рассмотрение для катушки индуктивности приводит к результату:
 | (7) |
Общий случай
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса. Импеданс находится по обычным правилам расчёта сопротивления сложной цепи, то есть используются формулы для сопротивления при параллельном и последовательном соединении резисторов. При этом все математические операции производятся по правилам действий над комплексными числами. Например, импеданс последовательно соединенных резистора, конденсатора и катушки индуктивности будет равен:
 | (8) |
Экспериментальное измерение импеданса
Импеданс реальных элементов может быть измерен специальными приборами: измерителем RLC или анализатором импеданса. Эти приборы позволяют производить измерения в широком диапазоне частот и при различных напряжениях смещения.
Применение импеданса
Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал.