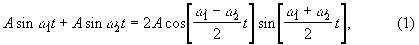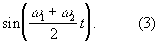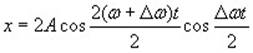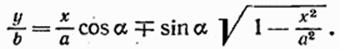Что такое биения чему равна частота биений период

Биения

Полезное

Смотреть что такое «Биения» в других словарях:

БИЕНИЯ — БИЕНИЯ, периодические изменения интенсивности колебаний. Биения получаются в результате сложения двух гармонических колебаний с близкими по величине частотами. В акустике биения слышны как периодические изменения силы звука. Биения являются также … Современная энциклопедия

Биения — БИЕНИЯ, периодические изменения интенсивности колебаний. Биения получаются в результате сложения двух гармонических колебаний с близкими по величине частотами. В акустике биения слышны как периодические изменения силы звука. Биения являются также … Иллюстрированный энциклопедический словарь

БИЕНИЯ — колебания с периодически изменяющейся амплитудой, возникающие при наложении 2 колебаний с близкими частотами f1 и f2. Биения используют для настройки музыкальных инструментов, а также для измерения частоты, емкости, индуктивности и т. д. Частота… … Большой Энциклопедический словарь

БИЕНИЯ — периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами. Б. возникают вследствие того, что разность фаз между двумя колебаниями с различными частотами всё время изменяется так, что… … Физическая энциклопедия

БИЕНИЯ — БИЕНИЯ, периодические изменения величины амплитуды при различного рода колебаниях. Возникают обычно при колебаниях связанных систем. Так, если подвесить рядом два маятника, соединить между собой их стержни (или нити, если маятник представляет… … Большая медицинская энциклопедия

биения — Ндп. биение Колебания, размах которых периодически колеблющаяся величина и которые являются результатом сложения двух гармонических колебаний с близкими частотами. [ГОСТ 24346 80] Недопустимые, нерекомендуемые биение Тематики вибрация EN beats DE … Справочник технического переводчика

Биения — – вибр. колебания, размах которых периодически колеблющаяся величина и которые являются результатом сложения двух гармонических колебаний с близкими частотами. [ГОСТ 24346 80] Рубрика термина: Виды вибрации Рубрики энциклопедии: Абразивное… … Энциклопедия терминов, определений и пояснений строительных материалов

Биения — График колебаний при биениях. Биения явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении … Википедия

биения — периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами f1 и f2. Биения используют для настройки музыкальных инструментов, а также для измерения частоты, ёмкости, индуктивности… … Энциклопедический словарь

БИЕНИЯ — в теории колебаний перио дич. изменения амплитуды результирующих не гармонич. колебаний, к рые возникают при наложении двух гармонических колебаний с близкими частотами. В простейшем случае Б., возникающих при наложении двух колебаний с равными… … Большой энциклопедический политехнический словарь

Источник

биения

Биения, возникающие в результате сложения двух гармонических колебаний с одинаковыми амплитудами и близкими частотами.

При сложении двух бегущих в одном направлении волн с близкими частотами и волновыми числами Б. возникают не только во времени, но и в пространстве. Складывая, напр., волны с равными амплитудами

получаем результирующую волну

с частотой и волновым числом , к-рые близки к частоте и волновому числу любой из компонент. Амплитуда волны модулирована в пространстве и времени медленно меняющейся огибающей с частотой и волновым числом. Частота Б. равна разности частот складываемых компонент .

При сложении двух волн с равными частотами и разными, но близкими по направлению волновыми векторами Б. возникают только в пространстве в результате интерференции волн (т. н. муар). Именно такую структуру имеют волны в френелевской зоне излучателей, а также волны в разл. волноводных системах.

Колебания в виде суперпозиции колебаний (или волн) с близкими частотами могут возникать в нелинейных системах. Так, если на нелинейное устройство, напр. квадратичный детектор, подать сумму двух колебаний, получим:

Измерение тона Б. лежит в основе точных измерений малых разностей двух близких частот, в частности сравнения нек-рой измеряемой частоты с эталонной.

Лит.: Горелик Г. С., Колебания и волны, 2 изд., M. 1959; Стрелков С. П., Введение в теорию колебаний 2 изд., M., 1964; Бишоп Р., Колебания, пер. с англ., 3 изд. M., 1986, Пейн Г., Физика колебаний и волн, пер. с англ M., 1979. В. А. Мельникова, В. Д. Шалфеев

Источник

Биения. 11-й класс

Е.М.РАВОДИН,
школа № 2, г. Прокопьевск,
Кемеровская обл.

Биения

Компьютерная поддержка. 11-й класс. Профильный курс

Напоминаем учащимся, что колебания подчиняются принципу суперпозиции. Значит, смещение точки, оказавшейся под воздействием двух колебаний, происходящих вдоль одной оси, равно алгебраической сумме смещений каждого колебания.

Рассмотрим случай сложения двух гармонических колебаний, которые мало отличаются по частоте: x₁ = A₁cos ₁t и x₂ = A₂cos ₂t, где А₁, А₂, ₁ и ₂ – соответственно их амплитуды и циклические частоты, причём || = |₂ – ₁| – очень малая величина. Найти результат сложения, т.е. рассчитать результирующее смещение Х = x₁ + x₂ можно так, как это описано, например, в учебнике Б.М.Яворского и А.А.Пинского «Основы физики», т. 2 (М.: Наука, 1974, с.18), а можно более наглядно и быстро с помощью созданной мною компьютерной программы skxxwd (cайт http://ssmu.ru/er/, раздел «Колебания», бесплатно).

Рассмотрим подробнее последний вариант. Программа skxxwd позволяет складывать колебания методом векторных диаграмм. Запустив программу, вводим через пробел начальную фазу, амплитуду и частоту первого колебания (например: 30 100 0.3). Нажав «Enter», видим на дисплее вектор, выражающий амплитуду первого колебания, наклонённый к оси Х под углом 30°. Вводим параметры второго колебания, у которого частота немного отличается от частоты первого (скажем, 90 150 и 0.28). Появляется второй вектор, отличающийся от первого по модулю и составляющий с ним угол 60°. Нажав пробел, наблюдаем вектор суммарного колебания, выделенный красным цветом. Следующий нажим пробела приводит к тому, что векторы начинают вращаться – каждый со своей угловой скоростью, равной круговой частоте колебаний. В результате амплитуда результирующего колебания периодически изменяется от суммы аплитуд складываемых колебаний (при совпадении фаз) до их разности (при противофазе). Поскольку частоты (а значит, и круговые частоты ₁ и ₂) почти одинаковы, то вращение результирующего вектора происходит с угловой скоростью _р

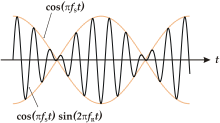
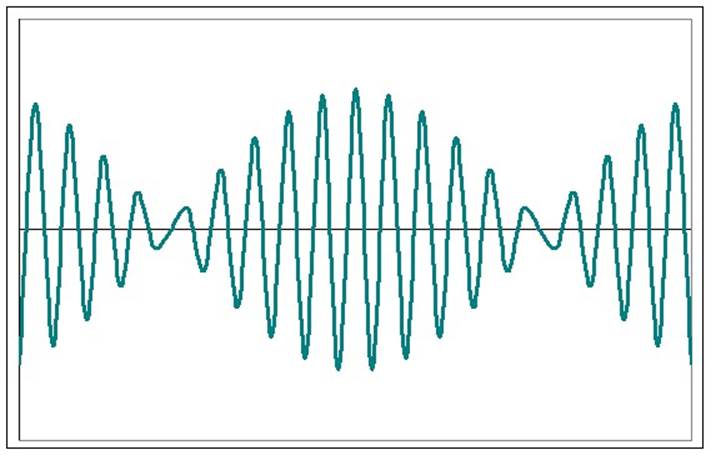
Соответствующие графики продемонстрирует другая программа, skxx-fur (см. там же). Выбрав в меню пункт 1, наблюдаем на экране графики двух колебаний с мало отличающимися частотами и их уравнения (экранная копия внизу слева). Нажав клавишу «пробел», видим результат их сложения – биения, т.е. колебания с периодически меняющейся амплитудой (экранная копия внизу справа).

Если в кабинете имеются два звуковых генератора с динамиками, то полезно показать биения звуковых колебаний. Для этого устаналиваем звуки с близкими частотами (например, 440 и 445 Гц) и слышим биения частотой 5 Гц. Сблизив частоты (доведя частоту второго колебания, к примеру, до 442 Гц), явственно наблюдаем уменьшение частоты биений.

При наличии микрофона и осциллографа процесс можно визуализировать: микрофон подключаем к Y-входу осциллографа, установив его наибольшую чувствительность и частоту развёртки 440 Гц. В соответствии с вариациями громкости наблюдаем изменение амплитуды на экране осциллографа.

Можно демонстрировать биения звуковых колебаний и при отсутствии звукового генератора. Берём два одинаковых камертона от прибора для демонстрации звукового резонанса (их собственные частоты 440 Гц) и на кончик ветви одного из них приклеиваем кусок пластилина массой 300 мг, – частота колебаний уменьшается приблизительно до 438 Гц. Заставив теперь звучать оба камертона одновременно, отчётливо слышим биения. Увеличив массу пластилина до 600 мг, ещё уменьшаем его частоту и отчётливо регистрируем на слух или по осциллограмме увеличение частоты биений.

В заключение полезно рассказать учащимся, что явление биений используется при настройке музыкальных инструментов. Настройщик заставляет одновременно звучать настраиваемую струну и эталонный камертон. Отсутствие биений указывает на то, что струна настроена правильно. Если биения слышны, то мастер, натягивая или ослабляя струну, добивается прекращения биений.

Наличием биений объясняется дребезжащий звук расстроенного фортепьяно. Высокие звуки в этом инструменте излучаются не одной струной, а несколькими, одновременно звучащими в унисон. Если какая-то струна колеблется не с той частотой, что остальные, то появляются биения, которые слушатели воспринимают как дребезжание.

Биения наблюдаются и в природе, например, периодическое усиление и ослабление волн во время бури. Моряки верят, что самым страшным является девятый вал, что отразил в своей знаменитой картине великий русский маринист И.К.Айвазовский.

Источник

Биения

Бие́ния — явление, возникающее при наложении двух гармонических колебаний, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала. Биения модулируются по амплитуде. Распространение такого вида колебаний менее эффективно. Частота изменения амплитуды суммарного сигнала равна разности частот двух исходных сигналов.

Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.

Биения звука можно слышать при настройке струнного музыкального инструмента по камертону. Если частота струны незначительно отличается от частоты камертона, то слышно, что звук пульсирует — это и есть биения. Струну нужно подтягивать или ослаблять так, чтобы частота биений уменьшалась. При совпадении высоты звука с эталонным биения полностью исчезают. Биения звука также можно услышать при игре на музыкальных инструментах, например пианино или гитаре, когда различной высоты звуки создают интервалы и многозвучия (аккорды).

Эффект биений можно использовать для преобразования частоты сигналов.

Ссылки

См. также

Полезное

Смотреть что такое «Биения» в других словарях:

БИЕНИЯ — БИЕНИЯ, периодические изменения интенсивности колебаний. Биения получаются в результате сложения двух гармонических колебаний с близкими по величине частотами. В акустике биения слышны как периодические изменения силы звука. Биения являются также … Современная энциклопедия

Биения — БИЕНИЯ, периодические изменения интенсивности колебаний. Биения получаются в результате сложения двух гармонических колебаний с близкими по величине частотами. В акустике биения слышны как периодические изменения силы звука. Биения являются также … Иллюстрированный энциклопедический словарь

БИЕНИЯ — колебания с периодически изменяющейся амплитудой, возникающие при наложении 2 колебаний с близкими частотами f1 и f2. Биения используют для настройки музыкальных инструментов, а также для измерения частоты, емкости, индуктивности и т. д. Частота… … Большой Энциклопедический словарь

БИЕНИЯ — периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами. Б. возникают вследствие того, что разность фаз между двумя колебаниями с различными частотами всё время изменяется так, что… … Физическая энциклопедия

БИЕНИЯ — БИЕНИЯ, периодические изменения величины амплитуды при различного рода колебаниях. Возникают обычно при колебаниях связанных систем. Так, если подвесить рядом два маятника, соединить между собой их стержни (или нити, если маятник представляет… … Большая медицинская энциклопедия

биения — Ндп. биение Колебания, размах которых периодически колеблющаяся величина и которые являются результатом сложения двух гармонических колебаний с близкими частотами. [ГОСТ 24346 80] Недопустимые, нерекомендуемые биение Тематики вибрация EN beats DE … Справочник технического переводчика

Биения — – вибр. колебания, размах которых периодически колеблющаяся величина и которые являются результатом сложения двух гармонических колебаний с близкими частотами. [ГОСТ 24346 80] Рубрика термина: Виды вибрации Рубрики энциклопедии: Абразивное… … Энциклопедия терминов, определений и пояснений строительных материалов

Биения — I Биения колебания с периодически меняющейся амплитудой, возникающие в результате наложения двух гармонических колебаний (См. Гармонические колебания) с несколько различными, но близкими частотами. Б. возникают вследствие того, что… … Большая советская энциклопедия

биения — периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами f1 и f2. Биения используют для настройки музыкальных инструментов, а также для измерения частоты, ёмкости, индуктивности… … Энциклопедический словарь

БИЕНИЯ — в теории колебаний перио дич. изменения амплитуды результирующих не гармонич. колебаний, к рые возникают при наложении двух гармонических колебаний с близкими частотами. В простейшем случае Б., возникающих при наложении двух колебаний с равными… … Большой энциклопедический политехнический словарь

Источник

Амплитуда биения. Сложение взаимно перпендикулярных колебаний

Векторная диаграмма.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) — фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой [1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.

Сложение нескольких гармонических колебаний одного направления.

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

(4.1)

Уравнение результирующего колебания будет иметь вид

Убедимся в этом, сложив уравнения системы (4.1)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

(4.2)

(4.3)

Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

Подставляя (4.3) в (4.2), получим:

Или окончательно, используя теорему косинусов суммы, имеем:

Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:

Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω

Биения, Период биения.

Бие́ния — явление, возникающее при наложении двух периодических колебаний, например, гармонических, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала.Частота изменения амплитуды суммарного сигнала равна разности частот исходных сигналов.

Период биений Т_б — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π.

Амплитуда биения. Сложение взаимно перпендикулярных колебаний.

Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:

где — разность фаз обоих колебаний.

Выражения (57.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (57.1) параметр t. Из первого уравнения следует, что

Теперь развернем косинус во втором из уравнений (57.1) по формуле для косинуса суммы, подставляя при этом вместо их значения (57.2) и (57.3). В результате получим

Последнее уравнение после несложных преобразований можно привести к виду

Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд а и b и разности фаз

Определим форму траектории для некоторых частных случаев.

1. Разность фаз а равна нулю. В этом случае уравнение (57.4) принимает вид

откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой и амплитудой, равной (рис. 57.1).

2. Разность фаз а равна Уравнение (57.4) имеет вид

откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 57.2)

3. При уравнение (57.4) переходит в

т. е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний.

При равенстве амплитуд а и эллипс вырождается в окружность.

Случаи отличаются направлением движения по эллипсу или по окружности. Если уравнения (57.1) можно записать следующим образом:

В момент тело находится в точке (рис. 57.3). В последующие моменты времени координата х уменьшается, а координата у становится отрицательной. Следовательно, движение совершается по часовой стрелке.

При уравнения колебаний имеют вид

Отсюда можно заключить, что движение происходит против часовой стрелки.

Из сказанного следует, что равномерное движение по окружности радиуса R с угловой скоростью со может быть представлено как сумма двух взаимно перпендикулярных колебаний:

(57.10)

(знак «+» в выражении для у соответствует движению против часовой стрелки, знак «—» — движению по часовой стрелке).

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В самом деле, уравнения колебаний можно представить следующим образом:

и выражение рассматривать как разность фаз, медленно изменяющуюся со временем по линейному закону.

Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от до

Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 57.4 показана одна из простейших траекторий, получающаяся при отношении частот 1 : 2 и разности фаз Уравнения колебаний имеют вид

За то время, пока вдоль оси х точка успевает переместиться из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение.

При отношении частот 1:2 и разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (рис. 57.5), по которой точка движется туда и обратно.

Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 57.6 для примера показана кривая для отношения частот 3 : 4 и разности фаз .

Источник