Что такое действительное отклонение в метрологии
Что такое действительное отклонение в метрологии
Limits and fits. Basic definitions
Дата введения 1963-01-01
1. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Комитетом стандартов, мер и измерительных приборов при Совете Министров СССР 26.03.62
3. ССЫЛОЧНЫЕ НОРМАТИВНО-ТЕХНИЧЕСКИЕ ДОКУМЕНТЫ
Обозначение НТД, на который дана ссылка
Номер пункта, приложения
4. Ограничение срока действия снято Постановлением Госстандарта СССР от 16.07.80 N 3626
5. ИЗДАНИЕ с Изменениями N 2, 3, утвержденными в мае 1970 г., июле 1980 г., (ИУС 5-70, 9-80)
1. Настоящий стандарт распространяется на гладкие цилиндрические соединения и плоские соединения с параллельными плоскостями* и устанавливает основные определения для системы допусков и посадок ОСТ, определяемой следующими стандартами: ГОСТ 11472, ГОСТ 8809, ГОСТ 3047, ОСТ НКМ 1011, ОСТ НКМ 1041, ОСТ 1012, ОСТ 1042, ОСТ 1043, ОСТ 1044, ОСТ НКМ 1016, ОСТ 1013, ОСТ 1069, ОСТ НКМ 1017, ОСТ 1014, ОСТ 1015, ОСТ НКМ 1021, ОСТ 1022, ОСТ 1142, ОСТ 1143, ОСТ НКМ 1026, ОСТ 1023, ОСТ НКМ 1027, ОСТ 1024, ОСТ 1025, ОСТ 1010, ГОСТ 2689, ГОСТ 11710.
* Применение стандарта для вновь разрабатываемых изделий не допускается.
1. Предельные отклонения и допуски, устанавливаемые стандартами на допуски и посадки, относятся к деталям, размеры которых определены при нормальной температуре 20 °С по ГОСТ 9249.
(Измененная редакция, Изм. N 3).
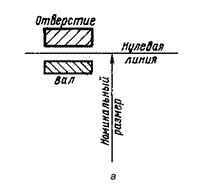
Примечание. Названия «отверстие» и «вал» условно применимы также и к другим охватывающим и охватываемым поверхностям.
3. Номинальным размером называется основной размер, определенный исходя из функционального назначения детали и служащий началом отсчета отклонений. Общий для отверстия и вала, составляющих соединение, номинальный размер называется номинальным размером соединения.
2. Номинальные размеры должны выбираться по ГОСТ 6636.
4. Действительным размером называется размер, полученный в результате измерения с допустимой погрешностью.
Примечание. Предельными размерами ограничиваются действительные размеры годных деталей, полученные измерением с допустимой погрешностью. Случаи, когда предельными размерами должны ограничиваться действительные размеры с учетом погрешностей измерения, следует оговаривать особо.
6. Отклонением размера называется алгебраическая разность между размером и его номинальным значением. Отклонение является положительным, если размер больше номинального, и отрицательным, если размер меньше номинального.
Действительным отклонением называется алгебраическая разность между действительным и номинальным размерами.
7. Допуском размера называется разность между наибольшим и наименьшим предельными размерами.
9. Полем допуска называется интервал значений размеров, ограниченный предельными размерами; оно определяется величиной допуска и его расположением относительно номинального размера. На схеме поле допуска изображается зоной между линиями, соответствующими верхнему и нижнему предельным отклонениям.
10. Размеры поверхности считаются находящимися в поле допуска, если в поле допуска находятся как измеренные двухточечным методом размеры проверяемой детали в любом месте поверхности, так и размеры геометрически правильного прототипа сопрягаемой детали, плотно (без зазора и натяга) сопрягающегося с проверяемой деталью.
Случаи, когда допускаются отступления от этого правила, должны быть оговорены особо.
Примечание. Приведенное в п.10 правило не предопределяет методику контроля.
11. Посадкой называется характер соединения деталей, определяемый величиной получающихся в нем зазоров или натягов. Посадка характеризует большую или меньшую свободу относительного перемещения соединяемых деталей или степень сопротивления их взаимному смещению.
12. Зазором называется положительная разность между размерами отверстия и вала (размер отверстия больше размера вала).
Натягом называется положительная разность между размерами вала и отверстия до сборки деталей (размер вала больше размера отверстия).
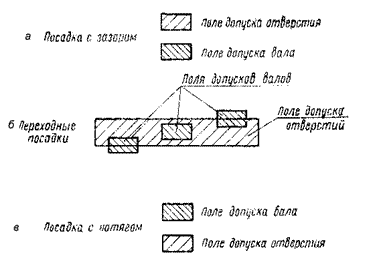
13. Посадки подразделяются на три группы:
а) посадки с зазором, при которых обеспечивается зазор в соединении;
б) посадки с натягом, при которых обеспечивается натяг в соединении;
в) переходные посадки, при которых возможно получение как натягов, так и зазоров.
Деление посадок по группам в стандартах на допуски и посадки производится в зависимости от взаимного расположения полей допусков отверстия и вала. К посадкам с зазором относятся посадки, в которых поле допуска отверстия расположено над полем допуска вала, в том числе и «скользящие» посадки, в которых нижняя граница поля допуска отверстия совпадает с верхней границей поля допуска вала.
К посадкам с натягом относятся посадки, в которых поле допуска вала расположено над полем допуска отверстия. К переходным посадкам относятся посадки, в которых поля допусков отверстия и вала перекрываются (черт.2).
14. Наибольшим и наименьшим зазором (или натягом) называются два предельных значения, между которыми должен находиться зазор (или натяг).
15. Допуском посадки называется разность между наибольшим и наименьшим зазорами (в посадках с зазором) или наибольшим и наименьшим натягом (в посадках с натягом).
В переходных посадках допуск посадки равен алгебраической разности между наибольшим и наименьшим натягами или сумме наибольшего натяга и наибольшего зазора.
16. Системой отверстия называется совокупность посадок, в которых предельные отклонения отверстий одинаковы (при одном и том же классе точности и одном и том же номинальном размере), а различные посадки достигаются путем изменения предельных отклонений валов (черт.3). Во всех стандартных посадках системы отверстия нижнее отклонение отверстий равно нулю. Такое отверстие называется основным отверстием.
Что такое действительное отклонение в метрологии
Основные нормы взаимозаменяемости
ЕДИНАЯ СИСТЕМА ДОПУСКОВ И ПОСАДОК
Общие положения, ряды допусков и основных отклонений
Basic norms of interchangeability. Unified system of tolerances and fits. General, series of tolerances and fundamental deviations
Дата введения 1990-01-01
1. РАЗРАБОТАН И ВНЕСЕН Министерством станкостроительной и инструментальной промышленности СССР
2. УТВЕРЖДЕН И ВВЕДЕН В ДЕЙСТВИЕ Постановлением Государственного комитета СССР по стандартам от 11.04.89 N 983
3. ВЗАМЕН ГОСТ 25346-82
4. Стандарт полностью соответствует СТ СЭВ 145-88
5. Стандарт соответствует международному стандарту ИСО 286-1-88*
7. ИЗДАНИЕ с Поправками (ИУС 1-91, 5-92)
Настоящий стандарт распространяется на гладкие элементы деталей, цилиндрические и ограниченные параллельными плоскостями, а также на образованные ими посадки и устанавливает термины, определения и условные обозначения, допуски и основные отклонения системы допусков и посадок для размеров до 3150 мм и любых линейных размеров, если они не установлены другими стандартами.
1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
1.1. Термины и определения
Примечание. В дальнейшем в стандарте под термином «допуск» понимают «стандартный допуск».
Примечание. Применявшийся ранее термин «проходной предел» использовать не рекомендуется.
Примечание. Применявшийся ранее термин «непроходной предел» использовать не рекомендуется.
Примечание. Натяг можно определять как отрицательную разность между размерами отверстия и вала.
Погрешность измерений. Классификация
Погрешность средств измерения и результатов измерения.
Погрешности средств измерений – отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений (создающие так называемые инструментальные ошибки измерений).
Погрешность результата измерения – отклонение результата измерения от действительного (истинного) значения измеряемой величины.
Инструментальные и методические погрешности.
Методическая погрешность обусловлена несовершенством метода измерений или упрощениями, допущенными при измерениях. Так, она возникает из-за использования приближенных формул при расчете результата или неправильной методики измерений. Выбор ошибочной методики возможен из-за несоответствия (неадекватности) измеряемой физической величины и ее модели.
Причиной методической погрешности может быть не учитываемое взаимное влияние объекта измерений и измерительных приборов или недостаточная точность такого учета. Например, методическая погрешность возникает при измерениях падения напряжения на участке цепи с помощью вольтметра, так как из-за шунтирующего действия вольтметра измеряемое напряжение уменьшается. Механизм взаимного влияния может быть изучен, а погрешности рассчитаны и учтены.
Инструментальная погрешность обусловлена несовершенством применяемых средств измерений. Причинами ее возникновения являются неточности, допущенные при изготовлении и регулировке приборов, изменение параметров элементов конструкции и схемы вследствие старения. В высокочувствительных приборах могут сильно проявляться их внутренние шумы.
Статическая и динамическая погрешности.
Статические и динамические погрешности относятся к погрешностям результата измерений. В большей части приборов статическая и динамическая погрешности оказываются связаны между собой, поскольку соотношение между этими видами погрешностей зависит от характеристик прибора и характерного времени изменения величины.
Систематическая и случайная погрешности.
Систематическая погрешность измерения – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины. Систематические погрешности являются в общем случае функцией измеряемой величины, влияющих величин (температуры, влажности, напряжения питания и пр.) и времени. В функции измеряемой величины систематические погрешности входят при поверке и аттестации образцовых приборов.
Причинами возникновения систематических составляющих погрешности измерения являются:
Случайной погрешностью называют составляющие погрешности измерений, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Случайные погрешности определяются совместным действием ряда причин: внутренними шумами элементов электронных схем, наводками на входные цепи средств измерений, пульсацией постоянного питающего напряжения, дискретностью счета.
Погрешности адекватности и градуировки.
Погрешность градуировки средства измерений – погрешность действительного значения величины, приписанного той или иной отметке шкалы средства измерений в результате градуировки.
Погрешностью адекватности модели называют погрешность при выборе функциональной зависимости. Характерным примером может служить построение линейной зависимости по данным, которые лучше описываются степенным рядом с малыми нелинейными членами.
Погрешность адекватности относится к измерениям для проверки модели. Если зависимость параметра состояния от уровней входного фактора задана при моделировании объекта достаточно точно, то погрешность адекватности оказывается минимальной. Эта погрешность может зависеть от динамического диапазона измерений, например, если однофакторная зависимость задана при моделировании параболой, то в небольшом диапазоне она будет мало отличаться от экспоненциальной зависимости. Если диапазон измерений увеличить, то погрешность адекватности сильно возрастет.
Абсолютная, относительная и приведенная погрешности.
Абсолютная погрешность – алгебраическая разность между номинальным и действительным значениями измеряемой величины. Абсолютная погрешность измеряется в тех же единицах измерения, что и сама величина, в расчетах её принято обозначать греческой буквой – ∆. На рисунке ниже ∆X и ∆Y – абсолютные погрешности.
Относительная погрешность – отношение абсолютной погрешности к тому значению, которое принимается за истинное. Относительная погрешность является безразмерной величиной, либо измеряется в процентах, в расчетах обозначается буквой – δ.
Приведённая погрешность – погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Вычисляется по формуле
где Xn – нормирующее значение, которое зависит от типа шкалы измерительного прибора и определяется по его градуировке:
Приведённая погрешность является безразмерной величиной, либо измеряется в процентах.
Аддитивные и мультипликативные погрешности.
Различать аддитивные и мультипликативные погрешности легче всего по полосе погрешностей (см.рис.).
Если абсолютная погрешность не зависит от значения измеряемой величины, то полоса определяется аддитивной погрешностью (а). Иногда аддитивную погрешность называют погрешностью нуля.
Если постоянной величиной является относительная погрешность, то полоса погрешностей меняется в пределах диапазона измерений и погрешность называется мультипликативной (б). Ярким примером аддитивной погрешности является погрешность квантования (оцифровки).
Класс точности измерений зависит от вида погрешностей. Рассмотрим класс точности измерений для аддитивной и мультипликативной погрешностей:
– для аддитивной погрешности:
аддитивная погрешность
где Х – верхний предел шкалы, ∆0 – абсолютная аддитивная погрешность.
– для мультипликативной погрешности:
мультипликативная погрешность
порог чувствительности прибора – это условие определяет порог чувствительности прибора (измерений).
Что такое действительное отклонение в метрологии
Колчков В.И. ВЗАИМОЗАМЕНЯЕМОСТЬ и НОРМИРОВАНИЕ ТОЧНОСТИ. М.: Учебное пособие, 2009
2.2. Допуски и посадки (Подробнее ЗДЕСЬ)
Допуск всегда положителен. Он определяет допускаемое поле рассеяния действительных размеров годных деталей в партии, т. е. заданную точность изготовления. С уменьшением допуска качество изделий, как правило, улучшается, но стоимость производства увеличивается.
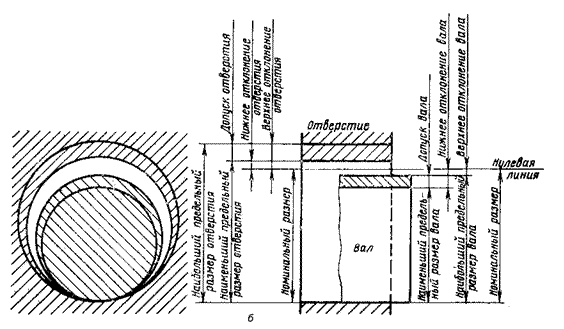
Для наглядного представления размеров, предельных отклонений и допусков, а также характера соединений используют графическое, схематическое изображение полей допусков, располагаемых относительно нулевой линии (рис.2.1).
Рис. 2.1 Поля допусков отверстия и вала при посадке с зазором (отклонения отверстия
положительны, отклонения вала отрицательны)
В готовых изделиях детали в большинстве случаев сопрягаются по своим формообразующим поверхностям, образуя соединения. Две или несколько подвижно или неподвижно соединяемых деталей называют сопрягаемыми. Поверхности, по которым происходит соединение деталей, называются сопрягаемыми поверхностями.Остальные поверхности называют несопрягаемыми (свободными). В соответствии с этим различают размеры сопрягаемых и несопрягаемых (свободных) поверхностей.
В соединении деталей, входящих одна в другую, есть охватывающие и охватываемые поверхности.
По степени свободы взаимного перемещения деталей различают следующие соединения:
В каждую из групп входит много разновидностей соединений, имеющих свои конструктивные особенности и свою область применения. В зависимости от эксплуатационных требований сборку соединений осуществляют с различными посадками.
Посадкой называется характер соединения деталей, определяемый величиной получающихся в нем зазоров или натягов.
Посадка характеризует большую или меньшую свободу относительного перемещения или степень сопротивления взаимному смещению соединяемых деталей. Тип посадки определяется величиной и взаимным расположением полей допусков отверстия и вала. Номинальный размер отверстия и вала, составляющих соединение является общим и называется номинальным размером посадки.
РМГ 29-2013 ГСИ. Метрология. Основные термины и определения
5 Результаты измерений
5.1 результат (измерения величины): Множество значений величины, приписываемых измеряемой величине вместе с любой другой доступной и существенной информацией.
1 Определение понятия результата измерения претерпело существенное изменение по сравнению с определением РМГ 29-99 и вобрало в себя выражение точности измерения. Информация, приводимая в результате измерения, определяется особенностями конкретного измерения и соответствует требованиям, предъявляемым к этому измерению. В большинстве случаев информация относится к точности измерения и выражается показателями точности, в обоснованных случаях содержит указание методики измерений и др.
2 Результат измерения может быть представлен измеренным значением величины с указанием соответствующего показателя точности. К показателям точности относятся, например, среднее квадратическое отклонение, доверительные границы погрешности, стандартная неопределенность измерений, суммарная стандартная и расширенная неопределенности. VIM3 [1] предусматривает также представление результата измерений плотностью распределения вероятностей на множестве возможных значений измеряемой величины.
3 Если значение показателя точности измерений можно считать пренебрежимо малым для заданной цели измерения, то результат измерения может выражаться как одно измеренное значение величины. Во многих областях это является обычным способом выражения результата измерения, с указанием класса точности применяемого средства измерений.
measurement result, result of measurement
5.2 измеренное значение (величины): Значение величины, которое представляет результат измерения.
1 Для измерения, в котором имеют место повторные показания, каждое показание может использоваться, чтобы получить соответствующее измеренное значение величины. Такая совокупность отдельных измеренных значений величины может быть использована для вычисления результирующего измеренного значения величины, такого как среднее арифметическое или медиана, обычно с меньшей соответствующей неопределенностью (погрешностью) измерений.
2 Когда диапазон истинных значений величины, представляющих измеряемую величину, мал по сравнению с неопределенностью (погрешностью) измерений, измеренное значение величины может рассматриваться как оценка, по сути дела, единственного истинного значения величины, и оно часто представляет собой среднее арифметическое или медиану отдельных измеренных значений, которые получены при повторных измерениях.
3 В случае, когда диапазон истинных значений величины, представляющих измеряемую величину, нельзя считать малым по сравнению с неопределенностью (погрешностью) измерений, измеренное значение часто будет оценкой среднего арифметического или медианы набора истинных значений величины.
4 В GUM [3] для понятия измеренное значение величины используют термины результат измерения и оценка значения измеряемой величины или просто оценка измеряемой величины. См. также 5.1, примечание 1.
measured quantity value, measured value of a quantity, measured value
5.3 опорное значение (величины): Значение величины, которое используют в качестве основы для сопоставления со значениями величин того же рода.
1 Опорное значение величины может быть истинным значением величины, подлежащей измерению, в этом случае оно неизвестно, или принятым значением величины, в этом случае оно известно.
2 Опорное значение величины со связанной с ним неопределенностью (погрешностью) измерений обычно приводят для:
— материала, например, аттестованного стандартного образца;
— устройства, например, стабилизированного лазера;
— референтной методики измерений;
reference quantity value, reference value
5.4 истинное значение (величины): Значение величины, которое соответствует определению измеряемой величины.
1 Определение измеряемой величины включает принятие некоторой модели объекта измерения, в которой истинное значение представлено неким параметром. Всегда существует пороговое несоответствие модели и объекта измерения, которое является причиной дефинициальной неопределенности измеряемой величины.
2 Когда дефинициальная неопределенность, связанная с измеряемой величиной, считается пренебрежимо малой по сравнению с остальными составляющими неопределенности измерений, измеряемая величина может рассматриваться как имеющая «по сути единственное» истинное значение. Такой подход принят в GUM [3] и в связанных с ним документах, где слово «истинный» считается излишним.
3 Существуют подходы оценивания точности измерений, которые избегают понятия истинного значения величины и опираются на понятие метрологической совместимости результатов измерения.
true quantity value, true value of a quantity, true value
5.5 принятое значение (величины): Значение величины, по соглашению приписанное величине для данной цели.
1 Иногда принятое значение величины является оценкой истинного значения величины.
2 Неопределенность измерений, связанная с принятым значением часто достаточна мала и может быть принята равной нулю для конкретной цели. В этом случае используют понятие действительное значение величины.
conventional quantity value, conventional value of a quantity, conventional value
5.6 действительное значение (величины): Значение величины, полученное экспериментальным путем и настолько близкое к истинному значению, что в поставленной измерительной задаче может быть использовано вместо него.
conventional true value of a quantity
5.7 точность измерений; точность результата измерения: Близость измеренного значения к истинному значению измеряемой величины.
measurement accuracy, accuracy of measurement, accuracy
5.8 правильность (измерений): Близость среднего арифметического бесконечно большого числа повторно измеренных значений величины к опорному значению величины.
1 Правильность измерений не является величиной и поэтому не может быть выражена численно, однако соответствующие показатели приведены в ISO 5725 [4].
2 Правильность измерений отражает близость к нулю систематической погрешности измерений.
measurement trueness, trueness of measurement, trueness
5.9 прецизионность (измерений): Близость между показаниями или измеренными значениями величины, полученными при повторных измерениях для одного и того же или аналогичных объектов при заданных условиях.
1 «Заданные условия» могут быть, например, условиями повторяемости измерений, условиями промежуточной прецизионности измерений или условиями воспроизводимости измерений (см. ISO 5725-1 [4]).
2 Понятие прецизионность измерений используется для определения понятий повторяемости измерений, промежуточной прецизионности измерений и воспроизводимости измерений.
3 Прецизионность измерений характеризует близость к нулю случайной погрешности измерений.
measurement precision, precision
5.10 условия повторяемости (измерений): Один из наборов условий измерений, включающий применение одной и той же методики измерений, того же средства измерений, участие тех же операторов, те же рабочие условия, то же местоположение и выполнение повторных измерений на одном и том же или подобных объектах в течение короткого промежутка времени.
repeatability condition of measurement, repeatability condition
5.11 повторяемость измерений: Прецизионность измерений в условиях повторяемости измерений.
measurement repeatability, repeatability
5.12 условия промежуточной прецизионности (измерений): Один из наборов условий измерений, включающий применение одной и той же методики измерений, то же местоположение и выполнение повторных измерений на одном и том же или аналогичных объектах в течение длительного периода времени, а также может включать другие условия, которые могут изменяться.
1 Изменения могут включать новые калибровки, калибраторы, средства измерений, а также новых операторов.
2 Описание условий должно включать все условия, изменяемые и неизменяемые, насколько это оправдано практически.
intermediate precision condition of measurement, intermediate precision condition
5.13 промежуточная прецизионность (измерений): Прецизионность измерений в фиксированных условиях промежуточной прецизионности измерений.
intermediate measurement precision, intermediate precision
5.14 условия воспроизводимости (измерений): Один из наборов условий измерений, включающий разные местоположения, разные средства измерений, участие разных операторов и выполнение повторных измерений на одном и том же или аналогичных объектах.
1 В исключительных случаях, разные средства измерений могут применяться в соответствии с разными методиками измерений.
2 Описание условий должно включать все условия, изменяемые и неизменяемые, насколько это оправдано практически.
reproducibility condition of measurement, reproducibility condition
5.15 воспроизводимость (измерений): Прецизионность измерений в условиях воспроизводимости измерений.
measurement reproducibility, reproducibility
5.16 погрешность (результата измерения): Разность между измеренным значением величины и опорным значением величины.
1 Если опорное значение величины известно, как, например, при калибровке средств измерений, то известно и значение погрешности измерения. Если в качестве опорного значения выступает истинное значение величины, то значение погрешности неизвестно.
2 В РМГ 29-99 использовался термин погрешность результата измерения: отклонение результата измерения от истинного (действительного) значения измеряемой величины. Изменение термина вызвано изменением понятия результат измерения (см. 5.1, примечание 1).
3 Погрешность измерения равна сумме случайной и систематической погрешностей.
measurement error, error of measurement, error
5.17 случайная погрешность (измерения): Составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных в определенных условиях.
random measurement error, random error of measurement, random error
5.18 среднее квадратическое отклонение; стандартное отклонение: Параметр функции распределения измеренных значений или показаний, характеризующий их рассеивание и равный положительному корню квадратному из дисперсии этого распределения.
1 Оценкой среднего квадратического отклонения является выборочное стандартное отклонение, определяемое по формуле

— среднее арифметическое из измеренных значений или показаний.
2 
3 Выборочное стандартное отклонение иногда неправильно называют средняя квадратическая погрешность.
5.19 систематическая погрешность (измерения): Составляющая погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной и той же величины.
1 В зависимости от характера изменения во времени систематические погрешности подразделяют на постоянные, прогрессирующие, периодические и погрешности, изменяющиеся по сложному закону. В зависимости от характера изменения по диапазону измерений систематические погрешности подразделяются на постоянные и пропорциональные.
Погрешности, изменяющиеся по сложному закону, происходят вследствие совместного действия нескольких систематических погрешностей.
2 Оставшуюся систематическую погрешность измерения после введения поправки называют неисключенной систематической погрешностью (НСП).
3 Для оценки систематической погрешности измерения в VIM3 [1] используется термин смещение (при измерении).
systematic measurement error, systematic error of measurement, systematic error
5.20 поправка: Значение величины, вводимое в показание с целью исключения систематической погрешности.
Компенсация может иметь различные формы, такие как дополнительное слагаемое или множитель, или она может находиться по соответствующей таблице.
5.21 поправочный множитель: Числовой коэффициент, на который умножают показание с целью исключения влияния систематической погрешности.
5.22 доверительные границы (погрешности измерения): Верхняя и нижняя границы интервала, внутри которого с заданной вероятностью находится значение погрешности измерений.
1 Доверительные границы при вероятности, равной 1, называют границами погрешности.
2 Доверительные границы погрешности иногда неправильно называют доверительная погрешность.
5.23 максимальная допускаемая погрешность (измерения): Максимальное значение погрешности измерения (без учета знака), разрешенное спецификацией или нормативными документами для данного измерения.
maximum permissible measurement error, maximum permissible error
5.24 погрешность метода (измерений): Составляющая погрешности измерений, обусловленная несовершенством принятого метода измерений.
5.25 инструментальная погрешность (измерения): Составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений.
5.26 абсолютная погрешность (измерения): Погрешность измерения, выраженная в единицах измеряемой величины.
absolute error of a measurement
5.27 относительная погрешность (измерения): Погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению измеряемой величины.


5.28 модель измерений; уравнение измерений: Уравнение связи между величинами в конкретной измерительной задаче.
measurement model, model of measurement, model
5.29 измерительная информация: Информация о значении величины, входящей в модель измерений.
5.30 функция измерений: Зависимость величин модели измерений, используемая для получения измеренного значения выходной величины по известным значениям входных величин.
5.31 входная величина (в модели измерений): Величина, которая должна быть измерена, или величина, значение которой может быть получено иным способом, для вычисления измеренного значения измеряемой величины.
1 Входная величина в модели измерений часто является выходной величиной средства измерений.
2 Входными величинами в модели измерений могут быть показания, поправки и влияющие величины.
input quantity in a measurement model, input quantity
5.32 выходная величина (в модели измерений): Величина, измеренное значение которой получают, используя значения входных величин в модели измерений.
output quantity in a measurement model, output quantity
5.33 влияющая величина: Величина, которая при прямом измерении не влияет на величину, которую фактически измеряют, но влияет на соотношение между показанием и результатом измерения.
1 Частота при прямом измерении постоянной амплитуды переменного тока с помощью амперметра.
2 Молярная концентрация билирубина при прямом измерении молярной концентрации гемоглобина в плазме крови человека.
3 Температура микрометра, применяемого для измерения длины стержня, но не температура самого стержня, которая может входить в определение измеряемой величины.
4 Фоновое давление в источнике ионов масс-спектрометра во время измерения молярной доли вещества.
1 Косвенное измерение включает комбинацию прямых измерений, каждое из которых может находиться под воздействием влияющих величин.
2 В GUM [3] понятие влияющая величина охватывает не только величины, влияющие на средство измерений, как в определении, приведенном выше, но также и те величины, которые влияют на фактически измеряемые величины. Кроме того, в GUM [3] это понятие не ограничивается прямыми измерениями.
5.34 неопределенность (измерений): Неотрицательный параметр, характеризующий рассеяние значений величины, приписываемых измеряемой величине на основании измерительной информации.
measurement uncertainty, uncertainty of measurement, uncertainty
5.35 стандартная неопределенность (измерений): Неопределенность измерений, выраженная в виде стандартного отклонения.
standard measurement uncertainty, standard uncertainty of measurement, standard uncertainty
5.36 суммарная стандартная неопределенность (измерений): Стандартная неопределенность измерений, которую получают суммированием отдельных стандартных неопределенностей измерений, связанных с входными величинами в модели измерений.
combined standard measurement uncertainty, combined standard uncertainty
5.37 расширенная неопределенность (измерений): Произведение суммарной стандартной неопределенности и коэффициента охвата большего, чем число один.
expanded measurement uncertainty, expanded uncertainty
5.38 интервал охвата: Интервал, основанный на имеющейся информации, который содержит совокупность истинных значений измеряемой величины с заданной вероятностью.
1 Если результат измерения представлен плотностью распределения вероятностей на множестве возможных значений измеряемой величины, то для любого интервала значений может быть вычислена соответствующая вероятность. Наличие плотности распределения вероятностей позволяет для заданной вероятности определить интервал значений измеряемой величины. Таких интервалов существует множество, обычно подразумевают наикратчайший интервал или интервал, симметричный относительно измеренного значения величины.
2 Интервал охвата не следует отождествлять с «доверительным интервалом» во избежание путаницы с этим статистическим понятием.
3 Интервал охвата может быть получен из расширенной неопределенности измерений.
5.39 вероятность охвата: Вероятность того, что совокупность истинных значений измеряемой величины находится в указанном интервале охвата.
5.40 коэффициент охвата: Число, большее чем один, на которое умножают суммарную стандартную неопределенность измерений для получения расширенной неопределенности измерений.
5.41 оценивание (неопределенности измерений) по типу А: Оценивание составляющей неопределенности измерений путем статистического анализа измеренных значений величины, получаемых при определенных условиях измерений.
Type A evaluation of measurement uncertainty, Type A evaluation
5.42 оценивание (неопределенности измерений) по типу В: Оценивание составляющей неопределенности измерений способами, отличными от оценивания неопределенности измерений по типу А.
— связанной со значениями величины, взятыми из авторитетных публикаций;
— связанной со значением аттестованного стандартного образца;
— полученной из сертификатов калибровки;
— связанной с классом точности поверенного средства измерений;
— полученной, исходя из пределов, установленных на основе опыта.
Type В evaluation of measurement uncertainty, Type В evaluation
5.43 бюджет неопределенности: Отчет о неопределенности измерений, составляющих неопределенности, их вычислении и суммировании.
5.44 дефинициальная неопределенность: Составляющая неопределенности измерений, являющаяся результатом ограниченной детализации в определении измеряемой величины.
1 Дефинициальная неопределенность есть практический минимум неопределенности измерений при любом измерении данной величины.
2 Любое изменение детализации в определении величины ведет к другой дефиницальной неопределенности.
5.45 целевая неопределенность (измерений): Верхняя граница неопределенности измерений, заранее установленная, исходя из предполагаемого использования результатов измерений.
target measurement uncertainty, target uncertainty
5.46 относительная стандартная неопределенность измерений: Стандартная неопределенность измерений, деленная на модуль измеренного значения величины.
relative standard measurement uncertainty
5.47 метрологическая совместимость (результатов измерений): Свойство множества результатов измерений для определенной измеряемой величины, при котором абсолютное значение разности любой пары измеренных значений величины, полученное из двух различных результатов измерений, меньше, чем некоторое выбранное кратное стандартной неопределенности измерений этой разности.
metrological compatibility of measurement results, metrological compatibility