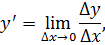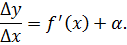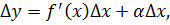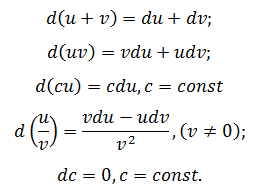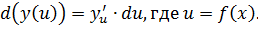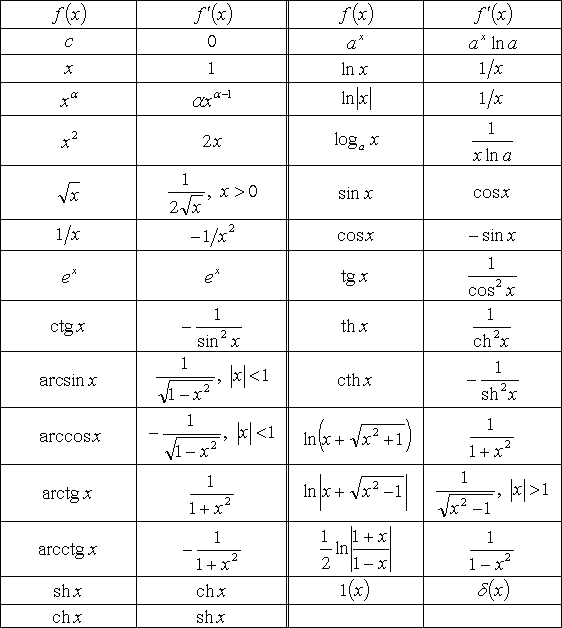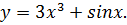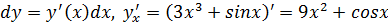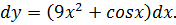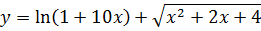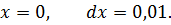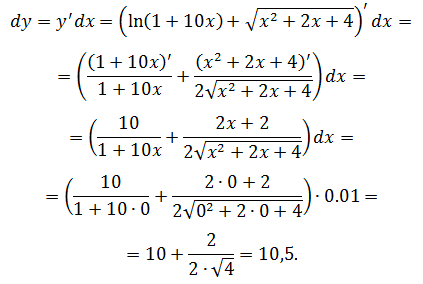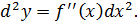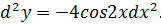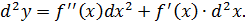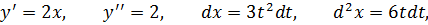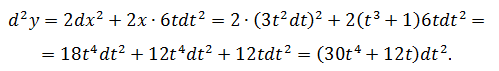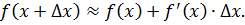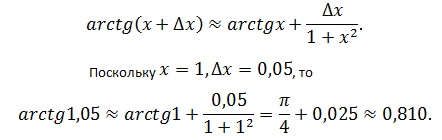Что такое дифференцирование в математике простыми словами

Зачем нужны эти производные?

Когда-то в школе я не понимал производных. Не подумайте, что я был совсем уж дураком — я знал определение, умел их брать (в рамках простеньких школьных примеров) и оценки по математике имел неплохие.

Но вот смысл этого понятия от меня ускользал. Я понимал насколько важен график некоторой функции — по нему легком можно увидеть зависимость функции от аргумента. Глянул в какую-нибудь точку — и сразу ясно положение дел в данном конкретном месте. И что с этого?

Смысл производной

Сложность подачи информации о производной заключается в том, что это одно из абстрактных понятий, физический смысл которых трудно представить наглядно. Если, например, численные величины, их сумму и произведение, возведение в степень несложно объяснить в понятиях окружающего мира (количество, площадь, объем и т.п.), то смысл производной зачастую ускользает от понимания школьников, поэтому они могут выполнять задачи на ее вычисление чисто механически по затверженным формулам.

Это ведет к тому, что в процессе решения учащийся не сможет справиться с заданиями, хоть немного отличающимися от шаблонных, и с такими неравенствами и системами уравнений, где надо применить навыки математического мышления.

Производная, как известно, характеризует скорость изменения функции в конкретной точке. Определение этого понятия звучит достаточно сложно:

«предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует».

Трудность понимания этого определения с точки зрения школьника можно охарактеризовать как «все слова по отдельности понятны, а общий смысл уловить не получается». Разумеется, без подробного и наглядного объяснения ученику останется лишь затучить эту фразу, не понимая ее смысла.

Допустим, два ученика одного класса — назовем их Иванов и Петров — получили за контрольную работу по теме «Системы уравнений и неравенств» по оценке «четыре». При этом Иванов весьма доволен, а Петров опечален. Такое их отношение к оценке станет понятным, если мы будем знать, что Петров — круглый отличник, а Иванов ни разу не получал по математике выше «тройки».

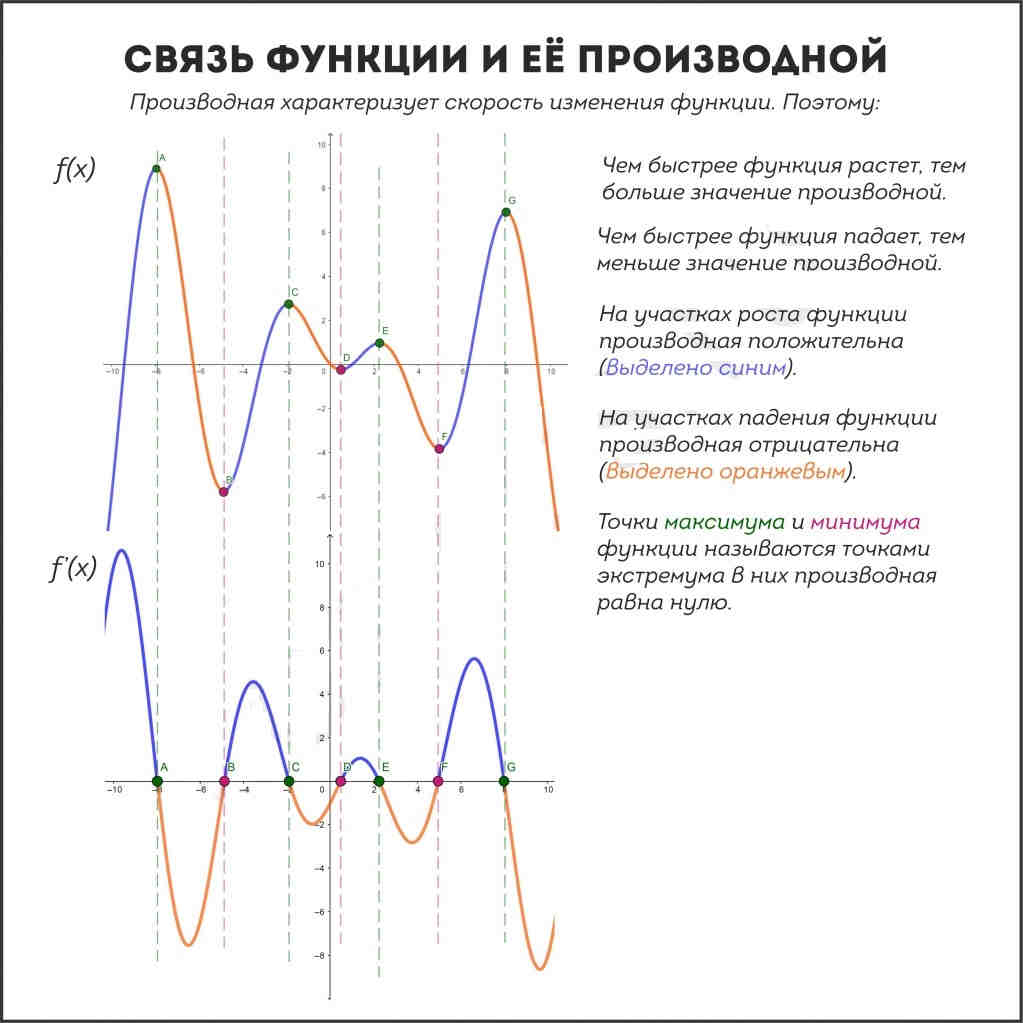
То есть, если рассматривать их оценки в динамике, мы видим, что у Иванова наблюдается прирост успеваемости (функция растет, ее производная положительна), а у Петрова, напротив, падение (функция убывает, производная отрицательна). То есть конкретная оценка (точка на графике функции) отображает текущее положение дел, а производная (касательная к графику в этой функции) показывает нам тенденцию развития ситуации.

Аналогично в физике: движение тел характеризуется не только скоростью, но и ускорением, то есть тем, увеличивается или уменьшается ли его скорость. На этих или других подобных примерах можно пояснить, что производная — важнейшая характеристика именно динамики любых процессов, то есть она описывает закон, по которому изменяется мгновенное значение любой функции.

И чтобы вообще добить.

А что такое производная от производной?

Если мы берем какую-то физическую величину, и берем от нее производную, например, от времени, это означает скорость возрастания этой физической величины от времени. Простой пример: берем расстояние, которое прошел человек, выражаем ее какой-то формулой, берем производную от этой формулы по времени, получаем- угадайте что? Скорость этого человека! Но, очень важно упомянуть, что мы получаем скорость этого человека от времени.

Круто! Значит, если мы возьмем производную от скорости по времени, то мы получим скорость возрастания. Скорости? Ну, да, как-то так.

Лично я всегда понимал все гораздо проще на примерах, поэтому:

Идет человек ранним утром, и пьет кофе. Каждый раз, когда он выпивает глоток, то его скорость увеличивается, но увеличивается постепенно. Значит, его скорость растет, значит человек ускоряется.

Итак, в общем случае, физический смысл производной- скорость роста той или иной величины в зависимости от той величины, по которой мы берем эту самую производную. Если мы возьмем производную еще раз, получим скорость возрастания скорости и так далее. Все просто (наверное)

Источник

Производная как смысл жизни или что такое дифференциал(d)

Пролог:

Эта одна из статей серии «Производная как смысл жизни», сначала я хотел сделать одну огромную статью про почти все темы по дифференцированию, но я передумал и сделаю несколько статей, возможно так даже будет легче для людей которые пытаются найти конкретную для себя тему.

Начало

Для начала лучше ознакомиться со статьей о самой прозводной (скоро будет). Ну если вы ознакомились, или уже были ознакомлены то идем дальше.

Как мы уже знаем формула записи производной выглядит так:

Мы должны понимать, что если мы уберем предел, то к f'(x) прибавиться коофициент, я ее называю «неточность».

Так же вполне логично, что при Δx->0, β->0, так как чем меньше мы делаем разницу между x и x₀, тем меньше значение «неточности»(в статье о производной об этом подробнее рассказано).

Теперь выразим из этого равенства приращение функции(Δy):

И на этом следует пока остановиться и рассмотреть график.

Смотрим дифференциалу в лицо

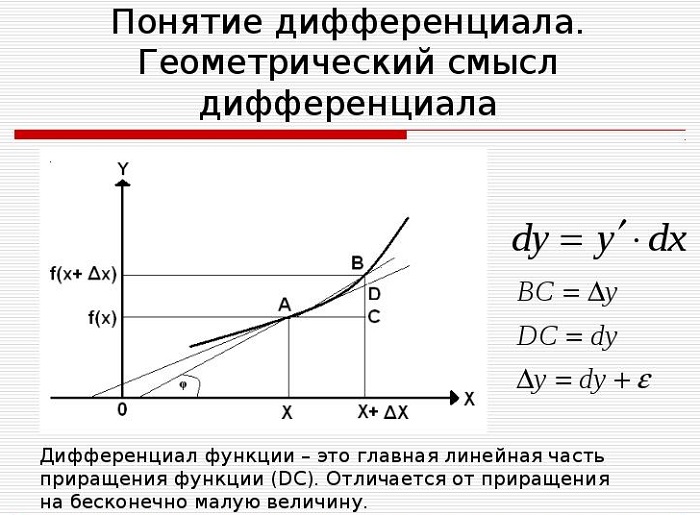
Расмотрим такой график:

Как мы знаем производная в точке равняется значению тангенса угла в этой точке, то есть f'(x)=tg(α). Так что давайте обозначим производную, ну и приращения которыми она ограничена.

Зная это введем обозначение на графике:

Вернемся к равенству

BD = Δy и мы знаем, что BD = BC + CD, а значит Δy = BC + CD, где BC мы назвали главной линейной частью приращения функции(dy), следовательно Δy = dy + βΔx.

Из формулы мы понимаем, что dy=f'(x)Δx.

Хорошо, мы определили чему равен дифференциал функции, а что же тогда является дифференциалом независимой пременной функции(аргумента).

Графически мы видим, что Δx никак не разделена касательной, то есть Δx это полное приращение функции, а значит dx = Δx.

Так же мы можем найти по формуле: dx = (x)’Δx = 1*Δx = Δx

И зная, что dy = f'(x)dx, мы можем выразить производную: f'(x)=dy/dx.

Немного пределов

Добавим с левой части и с правой предел

В самом начале мы сказали, что если β->0, то Δx->0 и наборот, а значит:

Зная, что f'(x)Δx = dy, мы делаем вывод, что:

Источник

При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции. Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.

Понятие и геометрический смысл дифференциала

Пусть y = f (x) имеет производную

Применяя свойства предела функции, получают равенство

После умножения обеих частей на приращение аргумента Δx, образуется тождество:

в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.

Определение 1

Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)).

Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x. Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.

Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.

Определение 2

Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.

Формы записи дифференциала

Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:

Отсюда получается формула:

Для второго порядка вводится обозначение d 2 y.

Свойства дифференциала

Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:

Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически,

Примеры решения задач

Задача №1

Найти дифференциал функции

Задача №2

Вычислить значение дифференциала функции

В помощь студентам создан онлайн калькулятор, который позволяет ввести функцию, нажать кнопку и получить форму или значение дифференциала.

Если dx есть константа, то для высших порядков имеет место следующая формула:

Этот результат вытекает непосредственно из определения:

Задача №3

Найти d 2 y, если y = cos2x и x – независимая переменная.

Если x – функция от некоторой другой независимой переменной, то свойство инвариантности перестаёт работать, следовательно,

Задача №4

Найти d 2 y, если y = x 2 и x = t 3 + 1, t – независимый аргумент.

Нетрудно заметить, что если выразить y напрямую через t, то получится тот же результат.

с высокой степенью точности можно вычислить приращение любой дифференцируемой зависимости.

Раскрыв Δy, сделав соответствующие преобразования, приходят к формуле приближённых вычислений:

Задача №5

Вычислить приближённо arctg1,05.

Пусть f(x) = arctg x. Тогда

Полный дифференциал функции

Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.

Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых.

Например, если z = f(x;y) то

Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.

Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.

Заключение

Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.

Источник

Решение производной для чайников: определение, как найти, примеры решений

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Иначе это можно записать так:

Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Пример. Вычислим производную:

Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

Пример: найти производную функции:

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Что такое дифференциал функции?

Понятие дифференциала функции связано с такими важными математическими разделами как дифференциальное и интегральное исчисление и тесно связано с понятием производной функции. Наиболее часто дифференциал применяется для приближенных вычислений, а также для оценки погрешностей формул и измерений.

Дифференциал функции — это линейная часть приращения функции. Говоря о значении дифференциала функции, рассматривают конкретную точку функции и бесконечно малое изменение аргумента.

История открытия дифференциала

Чаще всего открытие дифференциально-интегрального исчисления принято связывать с именем Исаака Ньютона, однако, этот факт активно оспаривают учёные со всего света.

Действительно, открытие целого нового направления в науке, столь значимого для её развития, было бы ошибочно считать заслугой только одного учёного. Изначально интегрирование связывали с вычислением площадей и объёмов криволинейных фигур. Такие задачи, как известно, решались ещё во времена Архимеда, поэтому его имя также имеет отношение к открытию дифференциального исчисления.

Также дифференцирование имеет отношение к решению задач на проведение касательных к различным кривым. Данное направление активно развивали греческие математики. В те времена математики столкнулись с трудностью, которую не смогли решить в дальнейшем и представители Нового времени.

Дело в том, что для определения направления прямой требовалось знать координаты как минимум двух точек, а касательная имеет лишь одну точку соприкосновения с кривой. Этот факт натолкнул учёных на мысль о том, что в одной точке кривая может иметь несколько касательных. В то время ученые пришли к выводу, что прямая состоит не из точек, а из отрезков минимальной длины. Таким образом, они считали направление касательной в некоторой точке совпадающим с направлением атомарного отрезка в данной точке.

В дальнейшем учёные Нового времени опровергли данную теорию. В этот период огромный вклад в развитие науки внёс Исаак Ньютон. Ученый сформулировал определения и принципы решения производных, а также основы дифференциального исчисления, которых придерживаются учёные и в наши дни.

Дифференциальное исчисление широко применяется в математике и других науках для решения различных задач.

Геометрический смысл дифференциала

Геометрический смысл дифференциала заключается в следующем: дифференциал функции f(x) равен приращению ординаты касательной к графику функции, которая проведена через некоторую точку с координатами (x,y) при изменении координаты x на величину Δх=dx.

Дифференциал является главной линейной частью функции относительно приращения аргумента. Чем меньше приращение функции, тем большая доля приращения приходится на эту линейную часть.

Таким образом, при бесконечно малом Δх, приращение функции можно считать равным ее дифференциалу. Это свойство дифференциала позволяет использовать его для приблизительных вычислений и оценки погрешностей измерений.

Применение дифференциала в приближенных вычислениях

Поскольку дифференциал функции является частью ее приращения, то при бесконечно малом приращении аргумента он приблизительно равен приращению функции. При этом чем меньше приращение аргумента, тем точнее значение функции. Этот факт даёт возможность использования дифференциалов для приближённых вычислений.

С помощью таких вычислений можно решать различные виды задач. Приближённые вычисления практически всегда связаны с наличием погрешности.

Использование дифференциала для оценки погрешностей

Результаты измерений в большинстве случаев содержат ошибку, обусловленную неточностью измерительных приборов.

Число, несколько превышающее или равное этой неточности, называется «предельной абсолютной погрешностью».

Отношение предельной погрешности к значению измеряемой величины называют «предельной относительной погрешностью».

Для оценки величины погрешностей измерений используют дифференциальное исчисление.

Источник