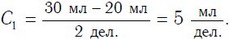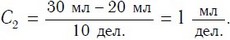Что такое нижний предел измерения прибора
§ 7. Измерительные приборы. Цена деления. Точность измерений
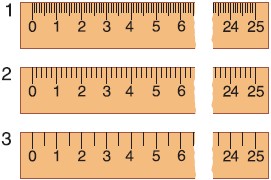
На рисунке 39 изображены три линейки с одинаковыми верхними пределами (25 см). Но эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 1, менее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала цену деления шкалы прибора.
Цена деления — это значение наименьшего деления шкалы прибора.
Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.
C1 = 1 см : 10 дел = 0,1 см/дел
C2 = 1 см : 5 дел = 0,2 см/дел
C3 = 1 см : 2 дел = 0,5 см/дел
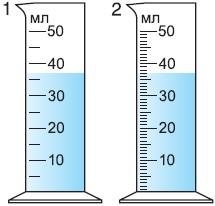
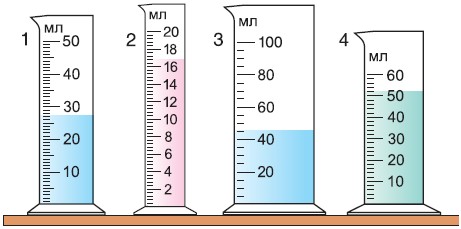
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 40). Цена деления шкалы мензурки 1:
Цена деления шкалы мензурки 2:
Измерим один и тот же объем мензуркой 1 и мензуркой 2. Исходя из показаний шкалы объем воды в мензурке 1:
V = 35 мл.
Из показаний шкалы мензурки 2:
V = 37 мл.
Понятно, что точнее измерен объем воды мензуркой 2, цена де- ления которой меньше (1 мл/дел
Шкала измерительного прибора, цена деления шкалы
Шкала — плоская или цилиндрическая поверхность, относительно которой движется стрелка, на которой нанесены деления.
Иногда шкала у прибора всего одна, а иногда их несколько, при этом индикатором измерений служит всего одна стрелка. Давайте же разберемся, что это за шкалы, и как ими пользоваться, чтобы ничего не напутать.
Для начала отметим, что шкалы эти бывают разными. Во-первых, более распространенными являются именованные шкалы, то есть шкалы, на которых деления проградуированы соответствующими единицами измеряемых величин, это градуированные шкалы.
Во-вторых, встречаются условные шкалы. Если прибор имеет несколько переключаемых пределов измерений, то шкала будет наверняка условной, и одни и те же деления будут иметь разные значения в каждом из установленных пользователем пределов.
Для того, чтобы по условной шкале прибора определить точно значение измеряемой в данный момент величины, необходимо, зная цену деления, количество делений до того места, куда отклонилась, и где остановилась в данный момент стрелка, умножить на цену деления.
Если цена деления не ясна, то ее можно легко найти, для этого берется разность между двумя известными значениями на шкале, и делится на количество делений между этими значениями. Например, известно, что красная шкала имеет ширину 10 вольт, а количество делений 50, значит цена деления для красной шкалы составляет 200 мВ.
Если на шкале есть отметка ноль, то шкала называется нулевой. Если нуля нет, то шкала называется безнулевой. Что касается нулевых шкал, то они, в свою очередь, подразделяются на односторонние и двухсторонние. На фото выше можно видеть сразу семь нулевых шкал.
У односторонних ноль размещен в самом начале шкалы (как на рисунке, головка вольтметра с односторонней шкалой), а у двухсторонних — по центру или между конечной и начальной отметками. Так, в зависимости от расположения нуля, двухсторонние шкалы подразделяются на несимметричные и симметричные.
Симметричная шкала ноль имеет по центру, несимметричная — не по центру шкалы. Если шкала безнулевая, то крайние отметки обозначают верхний и нижний пределы измерений. На фото выше изображен миллиамперметр с симметричной двухсторонней шкалой, цена деления составляет 50 мкА, поскольку 0,5 мА / 10 = 0,05 мА или 50 мкА.
В зависимости от характера связи угловых и линейных расстояний между двумя соседними делениями шкалы с измеряемыми величинами, шкалы бывают неравномерными, равномерными, логарифмическими, степенными и т. д. Для более точных измерений предпочтительней равномерные шкалы.
Когда отношение ширины самого широкого деления к самому узкому не более 1,3 при неизменной цене деления, шкалу уже можно считать равномерной.
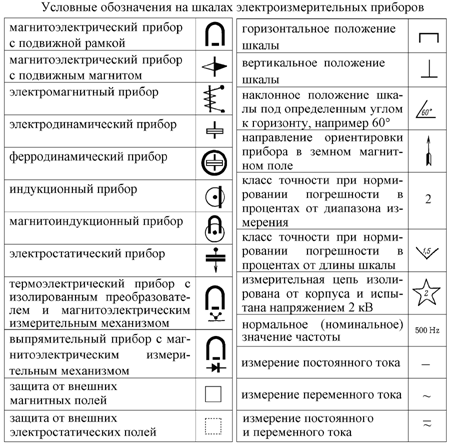
На лицевой стороне измерительного прибора, недалеко от шкалы, как правило, размещены необходимые маркировки: единица величины измерения, ГОСТ, класс точности прибора, число фаз и род тока, категория защищенности данного измерительного прибора от внешних электрических и магнитных полей, условия эксплуатации, рабочее положение, предельное напряжение прочности изоляции измерительных цепей (на фото — в звездочке «2», значит 2 кВ), номинальная частота тока, если отличается от промышленных 50 Гц, например 500 Гц, положение относительно Земли, тип, система прибора, год выпуска, заводской номер, и прочие важные параметры.
В этой таблице приведены расшифровки основных обозначений, которые можно встретить на шкалах. Надеемся, что эта краткая статья поможет вам научиться правильно проводить измерения при помощи стрелочных измерительных приборов.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Классификация по пределам и диапазонам измерения



Классификация по пределам и диапазонам измерения
Контроль отклонений расположения поверхностей в производственных условиях осуществляют с помощью проходных комплексных калибров. Людмила Фирмаль
Строго говоря, для многих приборов со шкалой 0 нижний предел измерения фактически не равен нулю. Точность измерения малых значений значительно снижается, поэтому нижний предел рабочей части шкалы должен быть определенным значением, составляющим 20-30% от верхнего предела. Многие приборы имеют устройства, которые могут изменять диапазон измерений в очень широком диапазоне. В этих случаях должен быть описан общий диапазон измерений, охватываемый измерительным устройством, и отдельные диапазоны, часто называемые отказом термина поддиапазон.
Есть три способа разделить общий диапазон на отдельные диапазоны. 1. Для каждого диапазона нижний предел измерения остается нулевым. Например, общий диапазон измерения 0-100 можно разделить на диапазон 0-0,1. 0-1; 0-10 и 0-100. 2. Общий диапазон делится на ряд равных последовательных диапазонов. Например, общий диапазон 0-5 делится на диапазон 0-1. 1-2; 2-3; 3-4; 4-5. 3. Как и во втором варианте, общий диапазон делится на последовательные диапазоны, но пределы измерения частично перекрываются. Например, общий диапазон 10-15000 делится на диапазон 10-150. 100-1500 и 1000-15000.
По виду контролируемой поверхности калибры подразделяют па калибры для контроля внутренней резьбы и калибры для контроля наружной резьбы. Людмила Фирмаль
Вышеприведенное выражение следует понимать так, чтобы оно было точным и грамматически правильным, и чтобы показанные характеристики относились только к ограниченному отображению. Многополосные характеристики прибора имеют свои преимущества и недостатки. Преимущество состоит в том, что один многополосный счетчик заменяет несколько однополосных счетчиков. Это дороже, чем каждая отдельная полоса, но дешевле, чем любое одноканальное устройство, которое оно заменяет. Кроме того, нет необходимости удалять одно устройство и устанавливать на его место другое устройство.
Если вам потребуется заказать решение по метрологии вы всегда можете написать мне в whatsapp.
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Лекция 3. МЕТРОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ
Метрологические характеристики прибора – это те, которые непосредственно связаны с его основным назначением – производством измерений. В эти характеристики входят пределы измерения, основная и дополнительные погрешности и класс точности.
Верхний и нижний пределы измерения ограничивают область (диапазон) использования прибора и поэтому представляют собой наиболее важную его характеристику. Чаще всего нижним пределом измерения прибора является нуль, что означает что, измеряемая величина, как таковая, отсутствует. Однако, это не всегда так. Иногда нуль располагается между верхним и нижним пределами и делит значения измеряемой величины на положительные и отрицательные. Пример – шкала термометра. Диапазон измерения
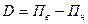
где 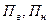
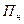
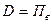
если же
При таком подходе (при условном постоянстве абсолютной погрешности) относительная погрешность измерения прибором (формула 1.7) приводится к виду
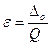
Таблица 3.2. Значения 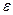
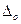
Числовые отметки, 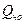 , МПа , МПа | ||||||
Относительные ошибки, 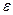 | — | 0.075 | 0.038 | 0.025 | 0.019 | 0.015 |
Из таблицы 3.2 (продолжение примера, данного в таблице 3.1) видно, что относительные погрешности максимальны на наименьшей числовой отметке и минимальны (равны классу точности) на наибольшей отметке. Это следует из формулы (3.7). Пример подтверждает правило, согласно которому разовые измерения желательно проводить в верхней трети шкалы. Это обеспечит наибольшую точность измерений.
Соответственно, ожидаемое значение измеряемой величины должно быть
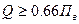
Наоборот, при выборе прибора для разовых измерений величины 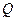
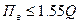
Требуемый класс точности определяют по заданной максимально допустимой относительной погрешности 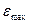
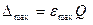
При выборе метрологических характеристик прибора непрерывного действиянеобходимо знать ожидаемый диапазон измеряемой величины от 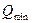
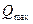
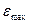
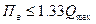
Максимальная абсолютная погрешность
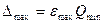
и приведенная погрешность 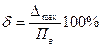
По приведенной погрешности из параметрического ряда выбирают соответствующий класс точности. Необходимо подчеркнуть, что при выборе приборав соответствии с заданной целью измерения, из ряда следует брать не ближайшее большее значение (как приоценкеточности прибора – см выше, формулы (3.4) – (3.6)), а наоборот, – ближайшее меньшее значение. В противном случае не выполняется требование непревышения заданного максимума относительной погрешности 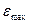
Для примера в таблице 3.3 заданы требования к исходным параметрам расхода
Таблица 3.3. Выбор метрологических характеристик бурового расходомера
| Параметр, символ, единица | Значение | Формула |
| Исходные данные | ||
Минимальный расход, 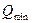 , л/с , л/с | ||
Максимальный расход, 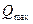 , л/с , л/с | ||
Максимальная относительная погрешность, 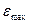 | 0.1 | |
| Результаты расчетов | ||
Верхний предел измерения расходомера, 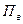 , л/с , л/с | (3.11) | |
Максимальная абсолютная погрешность, 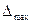 , л/с , л/с | 0.5 | (3.12) |
Приведенная погрешность, 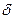 , % , % | 1.25 | (3.13) |
Класс точности, 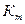 ,% ,% | (из параметрического ряда) | |
Основная погрешность, 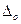 , л/с , л/с | 0.4 | (3.5) |
промывочной жидкости и по ним найдены метрологические характеристики расходомера.
Чем выше класс точности прибора, тем он дороже, сложнее в эксплуатации и обслуживании, чаще требует поверок и ремонтов. Поэтому надо стремиться использовать приборы возможно более низких классов точности, но при этом достигать необходимой точности измерений. Это достигается применением многопредельных приборов.
По формуле (3.12) принимающей вид 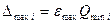
вычисляют 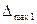
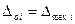
Преобразуя формулу (3.5), получают значение верхнего предела измерения
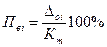
Принимают верхний предел первого диапазона за минимум измеряемой величины на втором диапазоне 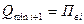
Далее определяют 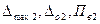
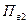
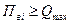
то выбирают двухдиапазонный прибор, иначе рассчитывают третий диапазон и т. д.
Пример. Для условий предыдущего примера ( 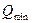
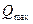
Таблица 3.4. Расчет многопредельного расходомера с классом точности 4%
| Параметр, символ, единица | Значение | Формула |
| Первый диапазон измерения | ||
Минимальный расход, 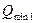 , л/с , л/с | (3.14) | |
Максимальная абсолютная погрешность, 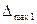 , л/с , л/с | 0.5 | (3.15) |
Основная погрешность, 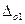 , л/с , л/с | 0.5 | (3.16) |
Верхний предел измерения расходомера, 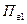 , л/с , л/с | (3.17) | |
| Второй диапазон измерения | ||
Минимальный расход, 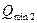 , л/с , л/с | (3.18) | |
Максимальная абсолютная погрешность, 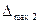 , л/с , л/с | 1.2 | (3.15) |
Основная погрешность, 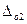 , л/с , л/с | 1.2 | (3.16) |
Верхний предел измерения расходомера, 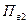 , л/с , л/с | 30* | (3.17) |
* Удовлетворяет условию (3.19), поэтому прибор остается двухдиапазонным
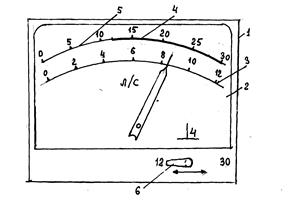
Рис.3.1 Расходомер с двухпредельной шкалой
1 – корпус показывающего прибора; 2 – циферблат; 3 – шкала нижнего диапазона; 4 – рабочая часть шкалы верхнего диапазона; 5 – нерабочая (относящаяся к нижнему диапазону) часть шкалы верхнего диапазона; 6 – переключатель диапазонов
На работу измерительного прибора и, в частности, на его точность, сильное влияние оказывают факторы внешней среды. К ним относятся климатические факторы, механические факторы, а для электрических приборов также и параметры питающей сети. Температура окружающего воздуха, его влажность, атмосферное давление относятся к климатическим факторам; наличие вибраций, сотрясений; ударов, пыли и брызгов – к механическим факторам; питающая сеть характеризуется напряжением и частотой.
Существуют так называемые нормальные условия измерения. Нормальными условиями измерения называют такие, при которых все влияющие факторы внешней среды находятся у значений (или в пределах некоторых интервалов значений), которые согласно паспорту данного прибора считаются нормальными. Так, нормальной температурой для большинства приборов, включая приборы контроля режима бурения, считается 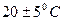
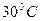
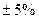
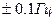
Выше указывалось, что при нормальных условиях измерения погрешность прибора не должна превышать значение его основной погрешности 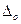
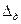
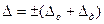
Дополнительная погрешность в этой формуле зависит от всех влияющих факторов, рассматриваемых вместе. Дополнительная погрешность по какому-то одному влияющему факторуА 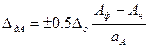
В этой формуле 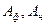
Таблица 3.5. Значения стандартного отклонения
| Наименование влияющего фактора | Стандартное отклонение 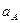 |
Температура окружающего воздуха, 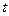 , градусов , градусов | |
Напряжение питающей сети, 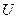 , % от номинального , % от номинального | |
Частота питающей сети, 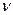 , Гц , Гц |
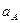
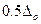
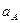
После установления дополнительных погрешностей, по всем, отклонившимся от нормальных условий факторам 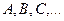
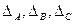
Таблица 3.6. Общая допустимая погрешность электрического манометра
| Параметр, символ, единица | Значение | Формула |
| Исходные данные | ||
Основная погрешность, 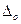 , МПа , МПа | 0.1 | |
Нормальная температура, 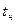 , град , град | ||
Фактическая температура, 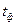 , град , град | ||
Стандартное отклонение температуры от нормальной, 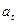 , град , град | ||
Нормальная частота сети, 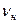 , Гц , Гц | ||
Фактическая частота сети, 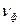 , Гц , Гц | ||
Стандартное отклонение частоты от нормальной, 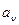 , Гц , Гц | ||
| Результаты расчетов | ||
Дополнительная погрешность по температуре, 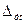 , МПа , МПа | 0.1 | (3.21) |
Дополнительная погрешность по частоте, 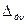 , МПа , МПа | 0.15 | (3.21) |
Суммарная дополнительная погрешность, 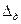 , МПа , МПа | 0.18 | (3.22) |
Общая допустимая погрешность, 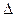 , МПа , МПа | 0.28 | (3.20) |
дополнительная погрешность определяется как
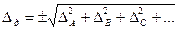
Пример нахождения общей допустимой погрешности манометра при отклонениях влияющих факторов внешней среды от нормальных условий приведен в таблице 3.6
Все измерительные приборы должны периодически – с периодичностью, указанной в их паспорте – проходить поверку. Часто такой период равняется одному году. Цель поверки – убедиться, что за очередной период эксплуатации основная и дополнительные погрешности прибора не вышли за допустимые пределы.
По отношению к поверке все приборы делятся на три группы: эталоны, образцовые приборы и рабочие приборы. Эталономназывается измерительное средство, обладающее наивысшей точностью, достижимой на данном этапе развития науки и техники. Так, если 50 лет назад эталоном метра было расстояние между насечками на платиноиридиевом стержне, то в наше время эталон метра считается равным 1650763.73 длин волны излучения, соответствующего оранжевой линии в спектре криптона-86. Абсолютная погрешность числа равна половине его последнего знака, т. е, в случае указанного числа длин волн – это 0.005 от длины одной волны (число заканчивается сотыми) Отсюда относительная погрешность (формула(1.7)) эталона метра 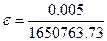
Существуют первичные, вторичные и третичные эталоны. Каждая основная единица системы СИ имеет свой эталон, хранящийся в Бюро мер и весов в Париже. Все государства, использующие систему СИ имеют одну копию этого эталона в качестве своего первичного-государственного эталона данной единицы. По первичному эталону, как по образцу, выполняется несколько вторичных эталонов, по ним – гораздо большее число третичных эталонов. Первичные эталоны постоянно находится на хранении в специальной организации (в России – это Институт метрологии им. Д.И. Менделеева в Санкт Петербурге). Все влияющие факторы внешней среды в помещении хранения строго стабилизированы. Третичные эталоны хранятся в крупных городах. По первичным эталонам периодически проходят поверку соответствующие вторичные эталоны, по вторичным – третичные эталоны, по третичным так называемые образцовые приборы.
Образцовые приборы служат для поверки, и градуировки рабочих приборов, используемых на различных производствах для контроля применяемой технологии. Поверять одни рабочие приборы с помощью других (пусть более точных) рабочих приборов запрещено. Используемый для поверки образцовый прибор должен иметь тот же диапазон измерения, что и поверяемый прибор. Основная погрешность образцового прибора должна быть не более 0.1 от основной погрешности поверяемого прибора (в исключительных случаях это соотношение может быть повышено до 0.33)
Процедура поверки заключается в том, что рабочий и образцовый приборы помещаются в одну и ту же измерительную магистраль (см., например рис. 2.1) поверочной установки. Поверка производится на всех числовых отметках (как в таблице 3.1), причем по формуле (1.6) определяется 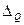
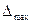
Если проверяется основная погрешность прибора, то ее вычисленное по формуле (3.5) значение сравнивают с 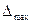
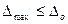
Если проводится поверка дополнительной погрешности, то прибор помещают в условия, когда рассматриваемый фактор 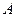
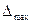
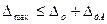
где 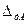
Если условия (3.23) и (3.24) соблюдены, то прибор выдержал поверку, и в его паспорте ставят соответствующую отметку с разрешением использования в течение следующего межповерочного срока. В противном случае прибор считается неисправным и его использование запрещается. Тогда он либо сдается на юстирование ( ремонт с целью повышения точности ), либо списывается.
Рекомендуемая литература: 1. с. 61-72.
1. Что такое пределы измерения прибора?
2. Что такое класс точности и как его находят?
3. Как выбрать прибор, если известны требования к результатам измерений?
4. Что такое основная и дополнительная погрешности измерительного прибора?
5. Как классифицируют измерительные средства, участвующие в поверке?