Что такое однозначные числа 2 класс
«Однозначные и двузначные числа» 2 класс
Тема урока : Однозначные и двузначные числа.
1) познакомить с понятиями «однозначные» и «двузначные» числа.
2) развивать навыки счёта, мышление учеников.
3) воспитывать аккуратность, уважение друг к другу, умение вовремя прийти на помощь.
Ну-ка проверь, дружок,
Ты готов начать урок?
Ручка, книжка и тетрадка?
Все ли правильно сидят?
Все ль внимательно глядят?
Тут затеи и задачи,
Игры, шутки – все для вас!
Пожелаю всем удачи.
За работу, в добрый час!
2.Задача на смекалку.
Яйцо всмятку варится 3 минуты. Сколько времени потребуется, что бы сварить 5 яиц? ( 3 минуты)
На дереве сидело 10 птиц. Охотник выстрелил и подстрелил одну птицу. Сколько птиц осталось на дереве? ( Ни одной птицы.)
Что тяжелее тонна пуха или тонна железа? ( одинаковый вес).
III. Изучение нового материала.
На доске записаны числа: 14, 5, 7, 60, 25, 2, 12, 1, 9, 10, 99.
– На какие группы можно разделить все числа?
(На доске учащиеся выписывают числа в две группы:
– Вспомните, как называются числа, в записи которых присутствует один знак (одна цифра). (Однозначными.)
– Как называются числа, в записи которых присутствуют два знака (две цифры)? (Двузначными.)
– Допишите группу однозначных чисел.
– Добавьте несколько чисел в группу двузначных чисел.
IV. Работа по теме урока.
Откройте учебник на стр.9.
-Чем похожи все однозначные числа?
-Чем похожи все двузначные числа?
Выполним № 1 на с. 9
— Прочитайте задание. Как вы будете его выполнять?
— Выполните задание самостоятельно.
Задание №3 – фронтальная работа. Как сравнить два числа?
— Что известно в задаче?
— Запишите краткое условие.
Рассмотрите рисунки в задании 7. Что вы увидели?
— Как вы думаете, сколько разных пар можно составить из этих овощей?
— Зарисуйте получившиеся у вас пары таким образом, чтобы в каждой паре были различные овощи.
V . Закрепление изученного.
Задание. Подчеркнуть одной чертой однозначные числа, двумя двузначные.
— Напишите два однозначных числа.
— Напишите два двузначных числа.
VI. Рефлексия. Подведение итогов урока.
-Какую тему мы изучали сегодня на уроке?
-Что нового вы узнали?
-Как называются числа, в записи которых одна цифра? (Однозначные).
-Как называются числа, в записи которых две цифры? (Двузначные).
— Молодцы! Спасибо за работу. Урок окончен.
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Похожие материалы
Математический диктант по теме «Простые и составные числа»
Конспект открытого урока по математике на тему » Умножение и деление смешанных дробей произвольного знака»
Математический диктант по теме «Признаки делимости»
Презентация к уроку математики в 5 классе на тему «Смешанные числа»
Контрольная работа за 1 полугодие
Презентация к уроку математики в 6 классе на тему «Прямая и обратная пропорциональные зависимости»
Конспект урока по математике для 4 класса «Строение задачи»
Презентация по математике на тему «Деление многозначного числа на однозначное» (4 класс)
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5398835 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования
Время чтения: 2 минуты
Росприроднадзор призвал ввести в школах курс по экологии
Время чтения: 1 минута
Рособрнадзор объявил сроки и формат ЕГЭ
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 5. Однозначные и двузначные числа. Миллиметр. Закрепление
Перечень вопросов, рассматриваемых в теме:
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.9, 10
2.. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с.8, 21, 41
Теоретический материал для самостоятельного изучения
Рассмотрим два числовых ряда и назовем в каждом лишнее число:
В первой ряду лишнее число три, потому что для записи этого числа потребовался один знак.
Во второй ряду чисел лишнее число шестнадцать, потому что в его записи два знака.
Числа, которые записываются двумя цифрами и обязательно содержат десятки, называются в математике двузначными. Числа, которые записываются одной цифрой, содержат только единицы, называются однозначными.
Мы уже знакомы с такими единицами длины как сантиметр и дециметр.
Более мелкая единица длины — это миллиметр.
Пишем «мм», а читаем «миллиметр».
6 мм, 6см, 6дм- это именованные числа: мм, см, дм показывают единицу измерения, а «6» показывает, сколько раз единица измерения содержится в числе.
Необходимо перевести в мм:
Перевести 88 мм в см и мм
88 мм нужно представить в сантиметрах и миллиметрах. В числе 88 мм содержится полных 8 сантиметров. Значит: 88 мм = 8 см 8 мм
Сравниваем единицы длины
1. Разделите числа на две группы.
1 группа: 9, 4, 6 (однозначные числа)
2 группа: 56, 12, 49 (двузначные числа)
2. Самая маленькая единица измерения длины;
Натуральные числа являются привычными человеку и интуитивно понятными, ведь они окружают нас с самого детства. В статье ниже мы дадим базовое представление о смысле натуральных чисел, опишем основные навыки их записи и чтения. Вся теоретическая часть будет сопровождаться примерами.
Общее представление о натуральных числах
На определенном этапе развития человечества возникла задача подсчета неких предметов и обозначение их количества, что, в свою очередь, потребовало нахождения инструмента для решения этой задачи. Таким инструментом и стали натуральные числа. Понятно и основное предназначение натуральных чисел – давать представление о количестве предметов или порядковом номере конкретного предмета, если речь идет о множестве.
Логично, что для использования человеком натуральных чисел, необходимо иметь способ их воспринимать и воспроизводить. Так, натуральное число можно озвучить или изобразить, что является естественными способами передачи информации.
Рассмотрим базовые навыки озвучивания (чтения) и изображения (записи) натуральных чисел.
Десятичная запись натурального числа
Теперь возьмем как правило, что при изображении (записи) любого натурального числа используются только указанные цифры без участия любых других символов. Пусть цифры при записи натурального числа имеют одинаковую высоту, записываются одна за другой в строчку и слева всегда находится цифра, отличная от нуля.
Верная запись натурального числа, произведенная с учетом всех описанных требований, называется десятичной записью натурального числа.
Количественный смысл натуральных чисел
Как уже было сказано, натуральные числа изначально несут в себе, в том числе, количественный смысл. Натуральные числа, как инструмент нумерации, рассмотрены в теме о сравнении натуральных чисел.
Далее, по аналогии: Ψ Ψ Ψ – 3 предмета («три»), Ψ Ψ Ψ Ψ – 4 («четыре»), Ψ Ψ Ψ Ψ Ψ – 5 («пять»), Ψ Ψ Ψ Ψ Ψ Ψ – 6 («шесть»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 7 («семь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 8 («восемь»), Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ Ψ – 9 («девять»).
С указанной позиции функция натурального числа заключается в указании количества предметов.
Однозначные натуральные числа
Однозначное натуральное число – натуральное число, при записи которого используется один знак – одна цифра.
Двузначные и трехзначные натуральные числа
Двузначные натуральные числа – натуральные числа, при записи которых используются два знака – две цифры. При этом используемые цифры могут быть как одинаковые, так и различные.
Рассмотрим, какой смысл заключен в двузначных числах. Опираться будем на уже известный нам количественный смысл однозначных натуральных чисел.
Введем такое понятие как «десяток».
Представим множество предметов, которое состоит из девяти и еще одного. В таком случае можно говорить об 1 десятке («один десяток») предметов. Если представить один десяток и еще один, то речь пойдёт о 2 десятках («два десятка»). Прибавив к двум десяткам еще один, получим три десятка. И так далее: продолжая добавлять по одному десятку, мы будем получать четыре десятка, пять десятков, шесть десятков, семь десятков, восемь десятков и, наконец, девять десятков.
Трехзначные натуральные числа – натуральные числа, при записи которых используются три знака – три цифры. Цифры могут быть различными или повторяющимися в любом сочетании.
Чтобы понять количественный смысл трехзначных натуральных чисел, введем понятие «сотня».
Одна сотня ( 1 сотня) – это множество, состоящее из десяти десятков. Сотня и еще одна сотня составят 2 сотни. Прибавим еще одну сотню и получим 3 сотни. Добавляя постепенно по одной сотне, получим: четыре сотни, пять сотен, шесть сотен, семь сотен, восемь сотен, девять сотен.
Так, трехзначное натуральное число 402 обозначает: 2 единицы, 0 десятков (отсутствуют десятки, не объединенные в сотни) и 4 сотни.
По аналогии дается определение четырёхзначных, пятизначных и так далее натуральных чисел.
Многозначные натуральные числа
От всего вышесказанного теперь возможно перейти к определению многозначных натуральных чисел.
Многозначные натуральные числа – натуральные числа, при записи которых используются два и более знаков. Многозначные натуральные числа – это двухзначные, трехзначные и так далее числа.
Одна тысяча – множество, включающее в себя десять сотен; один миллион состоит из тысячи тысяч; один миллиард – тысяча миллионов; один триллион – тысяча миллиардов. Еще более крупные множества также имеют названия, но использование их редко.
Аналогично принципу выше, мы можем рассмотреть любое многозначное натуральное число, как набор однозначных натуральных чисел, каждое из которых, находясь на определенном месте, свидетельствует о наличии и количестве единиц, десятков, сотен, тысяч, десятков тысяч, сотен тысяч, миллионов, десятков миллионов, сотен миллионов, миллиардов и так далее (справа налево соответственно).
Например, многозначное число 4 912 305 содержит в себе: 5 единиц, 0 десятков, три сотни, 2 тысячи, 1 десяток тысяч, 9 сотен тысяч и 4 миллиона.
Резюмируя, мы рассмотрели навык группировки единиц в различные множества (десятки, сотни и т.д.) и увидели, что цифры в записи многозначного натурального числа являются обозначением количества единиц в каждом из таких множеств.
Чтение натуральных чисел, классы
В теории выше мы обозначили названия натуральных чисел. В таблице 1 укажем, как верно использовать названия однозначных натуральных чисел в речи и при буквенной записи:
Один
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
Одна
Две
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
Одно
Два
Три
Четыре
Пять
Шесть
Семь
Восемь
Девять
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 1 2 3 4 5 6 7 8 9 | Один Два Три Четыре Пять Шесть Семь Восемь Девять | Одного Двух Трех Четырех Пяти Шести Семи Восьми Девяти | Одному Двум Трем Четырем Пяти Шести Семи Восьми Девяти | Один Два Три Четыре Пять Шесть Семь Восемь Девять | Одним Двумя Тремя Четырьмя Пятью Шестью Семью Восьмью Девятью | Об одном О двух О трех О четырех О пять О шести О семи О восьми О девяти |
Для грамотного прочтения и написания двузначных чисел, необходимо выучить данные таблицы 2 :
Мужской, женский и средний род
11
12
13
14
15
16
17
18
19
20
30
40
50
60
70
80
90
Одиннадцать
Двенадцать
Тринадцать
Четырнадцать
Пятнадцать
Шестнадцать
Семнадцать
Восемнадцать
Девятнадцать
Двадцать
Тридцать
Сорок
Пятьдесят
Шестьдесят
Семьдесят
Восемьдесят
Девяносто
| Число | Именительнный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 10 11 12 13 14 15 16 17 18 19 20 30 40 50 60 70 80 90 | Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто | Десяти Одиннадцати Двенадцати Тринадцати Четырнадцати Пятнадцати Шестнадцати Семнадцати Восемнадцати Девятнадцати Двадцати Тридцати Сорока Пятидесяти Шестидесяти Семидесяти Восьмидесяти Девяноста | Десять Одиннадцать Двенадцать Тринадцать Четырнадцать Пятнадцать Шестнадцать Семнадцать Восемнадцать Девятнадцать Двадцать Тридцать Сорок Пятьдесят Шестьдесят Семьдесят Восемьдесят Девяносто | Десятью Одиннадцатью Двенадцатью Тринадцатью Четырнадцатью Пятнадцатью Шестнадцатью Семнадцатью Восемнадцатью Девятнадцатью Двадцатью Тридцатью Сорока Пятидесятью Шестидесятью Семидесятью Восьмидесятью Девяностью | О десяти Об одиннадцати О двенадцати О тринадцати О четырнадцати О пятнадцати О шестнадцати О семнадцати О восемнадцати О девятнадцати О двадцати О тридцати О сорока О пятидесяти О шестидесяти О семидесяти О восьмидесяти О девяноста |
Для того, чтобы читать трёхзначные числа, изучим данные таблицы 3 :
Двести
Триста
Четыреста
Пятьсот
Шестьсот
Семьсот
Восемьсот
Девятьсот
| Число | Именительный падеж | Родительный падеж | Дательный падеж | Винительный падеж | Творительный падеж | Предложный падеж |
| 100 200 300 400 500 600 700 800 900 | Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот | Ста Двухсот Трехсот Четырехсот Пятисот Шестисот Семисот Восьмисот Девятисот | Ста Двумстам Тремстам Четыремстам Пятистам Шестистам Семистам Восьмистам Девятистам | Сто Двести Триста Четыреста Пятьсот Шестьсот Семьсот Восемьсот Девятьсот | Ста Двумстами Тремстами Четыремстами Пятистами Шестистами Семистами Восьмистами Девятистами | О ста О двухстах О трехстах О четырехстах О пятистах О шестистах О семистах О восьмистах О девятистах |
Чтобы легко прочитать указанные натуральные числа, занесем их в таблицу:
| Класс триллионов | Класс миллиардов | Класс миллионов | Класс тысяч | Класс единиц |
| 134 | 678 | |||
| 31 | 013 | 736 | ||
| 23 | 476 | 009 | 434 | |
| 2 | 533 | 467 | 001 | 222 |
Разберем подробно чтение числа 2 533 467 001 222 :
— добавив название класса, получим: «два триллиона»;
— читаем следующее число, добавив название соответствующего класса: «пятьсот тридцать три миллиарда»;
— продолжаем по аналогии, зачитывая следующий класс правее: «четыреста шестьдесят семь миллионов»;
— читаем последний класс единиц, не добавляя его название – «двести двадцать два».
Таким образом, число 2 533 467 001 222 будет звучать так: два триллиона пятьсот тридцать три миллиарда четыреста шестьдесят семь миллионов одна тысяча двести двадцать два. Используя указанный принцип, прочтем и прочие заданные числа:
— 31 013 736 – тридцать один миллион тринадцать тысяч семьсот тридцать шесть;
— 134 678 – сто тридцать четыре тысячи шестьсот семьдесят восемь;
— 23 476 009 434 – двадцать три миллиарда четыреста семьдесят шесть миллионов девять тысяч четыреста тридцать четыре.
Таким образом, основой правильного прочтения многозначных чисел является навык разбивать многозначное число на классы, знание соответствующих названий и понимание принципа прочтения двух- и трехзначных чисел.
Разряды натурального числа, значение разряда
Как уже становится понятно из всего вышесказанного, от позиции, на которой стоит цифра в записи числа, зависит ее значение. Т.е., например, цифра 3 в составе натурального числа 314 обозначает количество сотен, а именно – 3 сотни. Цифра 2 – количество десятков ( 1 десяток), а цифра 4 – количество единиц ( 4 единицы). При этом мы будем говорить, что цифра 4 находится в разряде единиц и является значением разряда единиц в заданном числе. Цифра 1 стоит в разряде десятков и служит значением разряда десятков. Цифра 3 располагается в разряде сотен и является значением разряда сотен.
Разряд – это позиция цифры в записи натурального числа, а также и значение этой цифры, которое определяется ее позицией в заданном числе.
Разряды имеют свои названия, мы уже использовали их выше. Справа налево следуют разряды: единиц, десятков, сотен, тысяч, десятков тысяч и т.д.
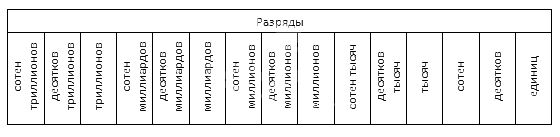
Для удобства запоминания можно использовать следующую таблицу (укажем 15 разрядов):
Уточним такую деталь: количество разрядов в заданном многозначном числе такое же, как количество знаков в составе записи числа. К примеру, данная таблица содержит названия всех разрядов для числа, в котором 15 знаков. Последующие разряды также имеют названия, но используются крайне редко и очень неудобны для восприятия на слух.
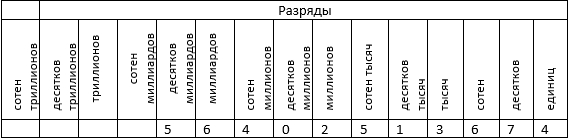
При помощи такой таблицы возможно наработать навык определения разряда, записывая заданное натуральное число в таблицу так, чтобы крайняя правая цифра была записана в разряде единиц и далее – в каждый разряд по цифре. К примеру, запишем многозначное натуральное число 56 402 513 674 так:
Введем также еще понятия низшего и высшего разрядов многозначного числа.
Низший (младший) разряд любого многозначного натурального числа – разряд единиц.
Высший (старший) разряд любого многозначного натурального числа – разряд, соответствующий крайней левой цифре в записи заданного числа.
Так, например, в числе 41 781 : низший разряд – разряд единиц; высший разряд – разряд десятков тысяч.
Логически следует, что возможно говорить о старшинстве разрядов относительно друг друга. Каждый последующий разряд при движении слева направо ниже (младше) предыдущего. И наоборот: при движении справа налево каждый следующий разряд выше (старше) предыдущего. К примеру, разряд тысяч старше разряда сотен, но младше разряда миллионов.
Уточним, что при решении некоторых практических примеров используется не само натуральное число, а сумма разрядных слагаемых заданного числа.
Кратко о десятичной системе счисления
Система счисления – метод записи чисел при помощи знаков.
Позиционные системы счисления – такие, в которых значение цифры в составе числа зависит от ее позиции в записи числа.
Помимо нее, существуют и прочие системы счисления. Например, информатика использует двоичную систему. Когда же мы ведем счет времени, то задействуем шестидесятеричную систему счисления.