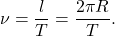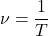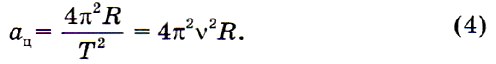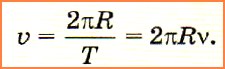Что такое период обращения как определить период обращения по окружности

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

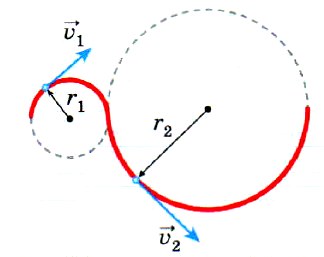
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Источник

Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: . Итак,

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

Частоту в СИ измеряют в

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Источник

Частная школа. 9 класс

Конспекты, контрольные, тесты

Период и частота

Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.

Период и частота

Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.

ПЕРИОД

Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.

Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.

С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.

ЧАСТОТА

Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.

Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?

Очевидно, ν = 1/Т = 1/20 1 /с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.

Таким образом, частота обращения является величиной, обратной периоду обращения:

СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ

Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:

или с учётом формулы (1):

С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:

Часто мгновенную скорость движения по окружности называют линейной скоростью.

Модуль скорости движения тела по окружности рассчитывается по формуле:

Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.

РЕШЕНИЕ ЗАДАЧ

Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.

Ответ: υ = 0,722 м/с.

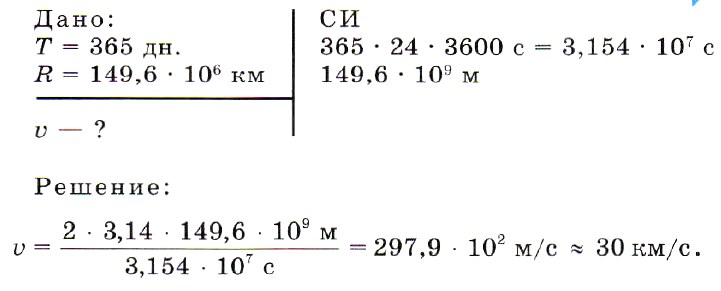
Задача 2. Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 10 6 км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.

Ответ: υ ≈ 30 км/с.

Вы смотрели Конспект по физике для 9 класса «Период и частота».

Источник

Равномерное движение тела по окружности

1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.

При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.

2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности ​ \( T \) ​ — время, в течение которого тело совершает один полный оборот. Единица периода — ​ \( [\,T\,] \) ​ = 1 с.

Связь между частотой и периодом обращения выражается формулой: ​ \( n=1/T \) ​.

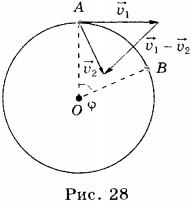
Пусть некоторое тело, движущееся по окружности, за время ​ \( t \) ​ переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол ​ \( \varphi \) ​.

Быстроту обращения тела характеризуют угловая и линейная скорости.

Угловая скорость ​ \( \omega \) ​ — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: ​ \( \omega=\varphi/t \) ​. Единица угловой скорости — радиан в секунду, т.е. ​ \( [\,\omega\,] \) ​ = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен ​ \( 2\pi \) ​. Поэтому ​ \( \omega=2\pi/T \) ​.

Линейная скорость тела ​ \( v \) ​ — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.

Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: ​ \( \vec=l/t \) ​. За один оборот точка проходит путь, равный длине окружности. Поэтому ​ \( \vec=2\pi\!R/T \) ​. Связь между линейной и угловой скоростью выражается формулой: ​ \( v=\omega R \) ​.

Из этого равенства следует, что чем дальше от центра окружности расположена точка вращающегося тела, тем больше её линейная скорость.

4. Ускорение тела равно отношению изменения его скорости ко времени, за которое оно произошло. При движении тела по окружности изменяется направление скорости, следовательно, разность скоростей не равна нулю, т.е. тело движется с ускорением. Оно определяется по формуле: ​ \( \vec=\frac<\Delta\vec>\) ​ и направлено так же, как вектор изменения скорости. Это ускорение называется центростремительным ускорением.

Центростремительное ускорение при равномерном движении тела по окружности — физическая величина, равная отношению квадрата линейной скорости к радиусу окружности: ​ \( a=\frac \) ​. Так как ​ \( v=\omega R \) ​, то ​ \( a=\omega^2R \) ​.

При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

1. При равномерном движении тела по окружности

1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости

2. Линейная скорость точки 1, находящейся на расстоянии ​ \( R_1 \) ​ от центра вращающегося колеса, равна ​ \( v_1 \) ​. Чему равна скорость ​ \( v_2 \) ​ точки 2, находящейся от центра на расстоянии ​ \( R_2=4R_1 \) ​?

1) ​ \( v_2=v_1 \) ​
2) ​ \( v_2=2v_1 \) ​
3) ​ \( v_2=0,25v_1 \) ​
4) ​ \( v_2=4v_1 \) ​

3. Период обращения точки по окружности можно вычислить по формуле:

1) ​ \( T=2\pi\!Rv \) ​
2) \( T=2\pi\!R/v \) ​
3) \( T=2\pi v \) ​
4) \( T=2\pi/v \) ​

4. Угловая скорость вращения колеса автомобиля вычисляется по формуле:

1) ​ \( \omega=a^2R \) ​
2) \( \omega=vR^2 \) ​
3) \( \omega=vR \)
4) \( \omega=v/R \) ​

5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?

1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась

6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?

1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза

7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?

1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза

8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?

9. Чему равна частота вращения точки обода колеса, если период обращения составляет 0,05 с?

1) 0,05 Гц
2) 2 Гц
3) 20 Гц
4) 200 Гц

10. Линейная скорость точки обода велосипедного колеса радиусом 35 см равна 5 м/с. Чему равен период обращения колеса?

1) 14 с
2) 7 с
3) 0,07 с
4) 0,44 с

11. Установите соответствие между физическими величинами в левом столбце и формулами для их вычисления в правом столбце. В таблице под номером физической
величины левого столбца запишите соответствующий номер выбранной вами формулы из правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
А) линейная скорость
Б) угловая скорость
В) частота обращения

ФОРМУЛА
1) ​ \( 1/T \) ​
2) ​ \( v^2/R \) ​
3) ​ \( v/R \) ​
4) ​ \( \omega R \) ​
5) ​ \( 1/n \) ​

12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение

ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась

Часть 2

13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?

Источник