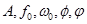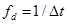Что такое периодические сигналы приведите пример

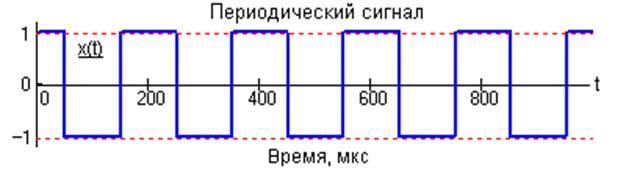
Что такое периодические сигналы приведите пример

Среди разнообразных систем ортогональных функций, которые могут использоваться в качестве базисов для представления радиотехнических сигналов, исключительное место занимают гармонические (синусоидальные и косинусоидальные) функции. Значение гармонических сигналов для радиотехники обусловлено рядом причин.

1. Гармонические сигналы инвариантны относительно преобразований, осуществляемых стационарными линейными электрическими цепями. Если такая цепь возбуждена источником гармонических колебаний, то сигнал на выходе цепи остается гармоническим с той же частотой, отличаясь от входного сигнала лишь амплитудой и начальной фазой.

2. Техника генерирования гармонических сигналов относительно проста.

2.1. Периодические сигналы и ряды Фурье

Математической моделью процесса, повторяющегося во времени, является периодический сигнал со следующим свойством:

Здесь Т — период сигнала.

Ставится задача найти спектральное разложение такого сигнала.

Ряд Фурье.

Зададим на отрезке времени рассмотренный в гл. I ортонормированцый базис, образованный гармоническими функциями с кратными частотами;

получим спектральное разложение

справедливое на всей бесконечности оси времени.

Ряд вида (2.4) называется рядом Фурье даннрго сигнала. Введем основную частоту последовательности, образующей периодический сигнал. Вычисляя коэффициенты разложения по формуле (2.3), запишем ряд Фурье для периодического сигнала

(2.6)

Итак, в общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую и бесконечный набор гармонических колебаний, так называемых гармоник с частотами кратными основной частоте последовательности.

Каждую гармонику можно описать ее амплитудой и начальной фазой Для этого коэффициенты ряда Фурье следует записать в виде

которая иногда оказывается удобнее.

Спектральная диаграмма периодического сигнала.

Так принято называть графическое изображение коэффициентов ряда Фурье для конкретного сигнала. Различают амплитудные и фазовые спектральные диаграммы (рис. 2.1).

Здесь по горизонтальной оси в некотором масштабе отложены частоты гармоник, а по вертикальной оси представлены их амплитуды и начальные фазы.

Рис. 2.1. Спектральные диаграммы некоторого периодического сигнала: а — амплитудная; б — фазовая

Особо интересуются амплитудной диаграммой, которая позволяет судить о процентном содержании тех или иных гармоник в спектре периодического сигнала.

Изучим несколько конкретных примеров.

Пример 2.1. Ряд Фурье периодической последовательности прямоугольных видеоимпульсов с известными параметрами , четной относительно точки t = 0.

В радиотехнике отношение называют скважностью последовательности. По формулам (2.6) находим

Окончательную формулу ряда Фурье удобно записать в виде

На рис. 2.2 представлены амплитудные диаграммы рассматриваемой последовательности в двух крайних случаях.

Важно отметить, что последовательность коротких импульсов, следующих друг за другом достаточно редко , обладает богатым спектральным составом.

Пример 2.2. Ряд Фурье периодической последовательности импульсов, образованной гармоническим сигналом вида ограниченным на уровне (предполагается, что ).

Введем специальный параметр — угол отсечки , определяемый из соотношения откуда

В соотаетствии с этим величина равна длительности одного импульса, выраженной в угловой мере:

Аналитическая запись импульса, порождающего рассматриваемую последовательность, имеет вид

Постоянная составляющая последовательности

Амплитудный коэффициент первой гармоники

Аналогично вычисляют амплитуды — гармонических составляющих при

Полученные результаты обычно записывают так:

где так называемые функции Берга:

Графики некоторых функций Берга приведены на рис. 2.3.

Рис. 2.3. Графики нескольких первых функций Берга

Комплексная форма ряда Фурье.

Спектральное разложение периодического сигнала можно выполнить и несколько ионному, используя систему базисных функций, состоящую из экспонент с мнимыми показателями:

Легко видеть, что функции этой системы периодичны с периодом ортонормированы на отрезке времени так как

Ряд Фурье произвольного периодического сигнала в данном случае принимает вид

Обычно используют следующую форму записи:

Выражение (2.11) представляет собой ряд Фурье в комплексной форме.

Спектр сигнала в соответствии с формулой (2.11) содержит компоненты на отрицательной полуоси частот, причем . В ряде (2.11) слагаемые с положительными и отрицательными частотами объединяются в пары, например:

Итак, отрицательная частота — понятие не физическое, а математическое, вытекающее из способа представления комплексных чисел.

Изображение периодического сигнала на комплексной плоскости.

Структура ряда Фурье (2.11) дает возможность изобразить периодический сигнал посредством бесконечной суммы вращающихся векторов на комплексной плоскости (рис. 2.4).

Построение осуществляется следующим образом. Из начала координат комплексной плоскости (точка О) строят вещественный вектор который отображает член, с номером

Рис. 2.4. Графическое отображение ряда Фурье в комплексной форме

Затем в формуле (2.11) полагают и строят суммы векторов

отвечающие вкладу слагаемых с положительными и отрицательными частотами. Если ряд Фурье сходится, то каждая из сумм отображается вектором конечной длины.

Как указывалось, коэффициенты ряда Фурье с положительными и отрицательными частотами комплексно сопряжены, поэтому вектор — всегда вещественный. Будучи сложен с постоянной составляющей он образует вектор, длина которого равна — значению сигнала в начальный момент времени.

Такая наглядная интерпретация спектрального разложения периодического сигнала будет использована в последующем параграфе.

Источник

Периодические и непериодические сигналы

Сигнал s(t) называется периодическим, если он точно повторяет свои значения через одинаковые промежутки времени

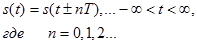При этом наименьший интервал повторения Т называется периодом, частота повторения f0=1/T называется основной частотой.

К периодическим сигналам относят гармонические и полигармонические сигналы.

-постоянные величины, которые могут исполнять роль информационных параметров сигнала: А – амплитуда сигнала, f0 –циклическая частота в герцах, ωо – угловая частота в радианах,

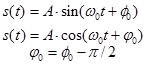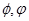
— начальные фазовые углы в радианах.

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов, и описывается суммой гармонических колебаний:

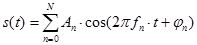
Полиграфические сигналы представляют собой сумму определенной постоянной составляющей (fо=0) и произвольного числа гармонических составляющих с произвольными значениями амплитуд An и фаз jn, с частотами, кратными фундаментальной частоте fp.

Периодический сигнал любой произвольной формы может быть представлен в виде суммы гармонических колебаний с частотами, кратным фундаментальной частоте колебаний fр = 1/Тр.

Непериодический сигнал – почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов, с произвольными частотами, отношение которых (хотя бы двух частот минимум ) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени.

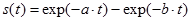
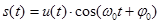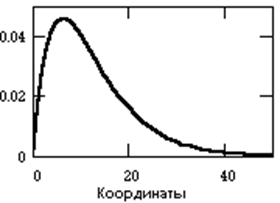
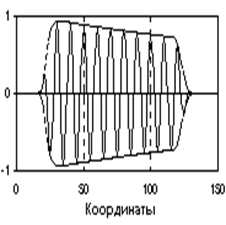
Случайным сигналом называют функцию времени, значения которой заранее неизвестны, и могут быть предсказаны лишь с некоторой вероятностью. Случайный сигнал отображает случайное физическое явление или физический процесс, причем, зарегистрированный в единичном наблюдении, сигнал не воспроизводится при повторных наблюдениях.

В качестве основных статистических характеристик случайных сигналов принимают:

а) закон распределения вероятности нахождения величины сигнала в определенном интервале значений;

б) спектральное распределение мощности сигнала.

Случайные сигналы подразделяют на стационарные и нестационарные. Стационарные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса.

Отдельную категорию сигналов составляют шумы (noise) и помехи – сигналы, искажающие интересующий сигнал.

Строго говоря, они не являются сигналами в исходном определении, т.к. не несут никакой полезной информации. Но в то же время, часто их называют сигналами в том смысле, что они имеют зависимость от той же независимой переменной, что и основной сигнал, и также порождаются физическими процессами.

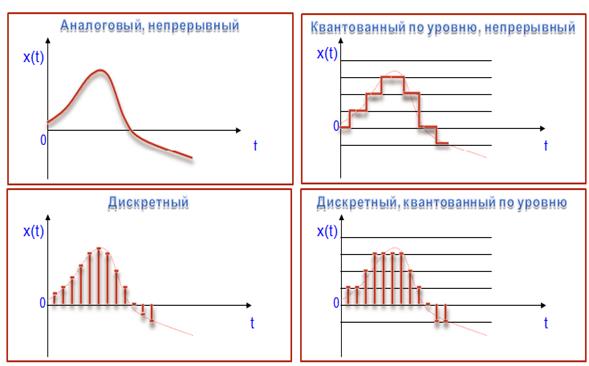
Классы детерминированных сигналов:

— произвольные по величине и непрерывные по времени (аналоговые);

— произвольные по величине и дискретные по времени (дискретные);

— квантованные по величине и непрерывные по времени (квантованные);

— квантованные по величине и дискретные по времени (цифровые).

Любой сигнал определенные возможные значения на определенном пространстве значений независимой переменной. Как значения, так и независимая переменная могут быть либо непрерывными, либо дискретными.

Непрерывность — свойство, заключающееся в постепенном, плавном, без скачков изменении значений какой-либо переменной, функции или другого математического объекта.

Дискретность — свойство, противопоставляемое непрерывности, прерывность.

Аналоговый (непрерывный) сигнал – сигнал, значения и независимая переменная которого являются непрерывными множествами возможных значений.

Дискретный сигнал – сигнал, независимая переменная которого определена на дискретном множестве, а значения являются непрерывными.

Аналоговый сигнал является непрерывной функцией времени, т.е. однозначно определяется для всех t. Электрический аналоговый сигнал возникает тогда, когда физический сигнал (например, речь) некоторым устройством преобразовывается в электрический.

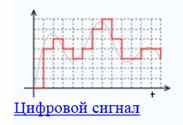
Цифровой сигнал—сигнал данных, у которого каждый из представляющих параметров описывается функцией дискретного времени и конечным множеством возможных значений.

Соответственно, можно определить следующие преобразования сигналов:

Дискретизация — процесс преобразования аналогового сигнала в дискретный.

Квантование — преобразование аналогового сигнала в квантованный.

Оцифровка — преобразование аналогового сигнала в цифровой.

Восстановление — преобразование сигнала из дискретного или цифрового в аналоговый.

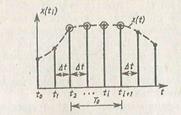
Частота дискретизации дискретного сигнала — частота следования отсчетов.

Период дискретизации — расстояние между двумя соседними отсчетами.

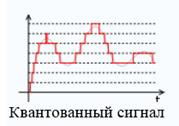
Квантование (quantization) — в информатике разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов.

Квантование по уровню — представление величины отсчѐтов цифровыми сигналами.

Для квантования в двоичном коде диапазон напряжения сигнала от Umin до Umax делится на 2n интервалов.

Величина получившегося интервала (шага квантования):

Сигнал, к которому применены дискретизация и квантование, называется цифровым.

Порядок выполнения лабораторной работы:

Создаем м-файл в среде MatLab: File>New>M-File

Источник

Связь между временной и частотной областями представления сигналов

Электрические сигналы можно исследовать во временной области с помощью осциллографа и в частотной области с помощью анализатора спектра (рисунок 1).

Рисунок 1 – Сигналы, исследуемые во временной и частотной областях

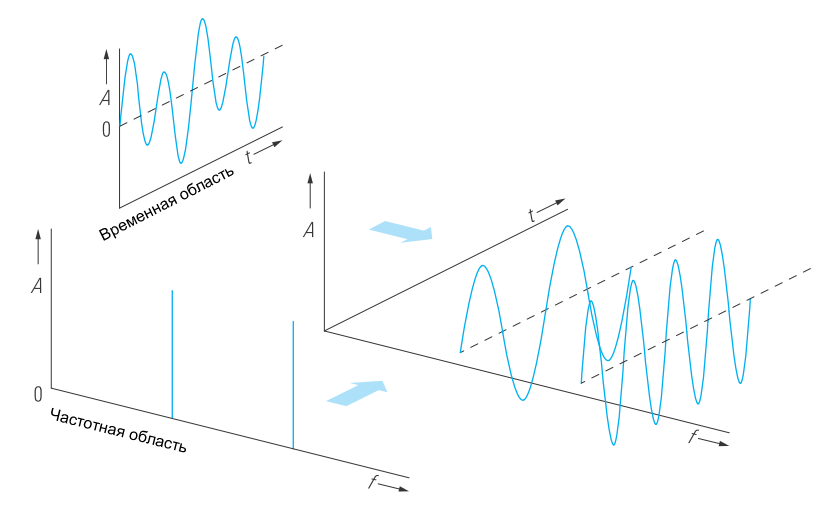
Эти два режима отображения сигналов связаны друг с другом преобразованием Фурье (обозначается как F), поэтому каждый сигнал во временной области имеет характерный частотный спектр. Таким образом, связь представлениями во временной и частотной областях будет следующей:

Чтобы проиллюстрировать эту взаимосвязь, сначала исследуем сигналы только с периодическим откликом во временной области.

Периодические сигналы

Согласно теореме Фурье любой сигнал, являющийся периодическим во временной области, может быть получен из суммы синусоидальных и косинусоидальных сигналов разной частоты и амплитуды. Такая сумма называется рядом Фурье. В этом случае применима следующая формула:

\[x(t) = \frac <2>+ \sum_^ <\infty>A_n \cdot \sin(n \cdot \omega_0 \cdot t) + \sum_^ <\infty>B_n \cdot \cos(n \cdot \omega_0 \cdot t) \qquad (3)\]

Коэффициенты Фурье A₀, A_n и B_n зависят от формы сигнала x(t) и могут быть рассчитаны следующим образом:

\[A_0 = \frac<2> \int_<0>^ x(t) \ dt \qquad (4)\]

\[A_n = \frac<2> \int_<0>^ x(t) \cdot \sin(n \cdot \omega_0 \cdot t) \ dt \qquad (5)\]

\[B_n = \frac<2> \int_<0>^ x(t) \cdot \cos(n \cdot \omega_0 \cdot t) \ dt \qquad (6)\]

На рисунке 2b показан прямоугольный сигнал, аппроксимированный в ряд Фурье. Отдельные компоненты этого ряда Фурье показаны на рисунке 2a. Чем больше этих компонентов, тем итоговый сигнал ближе к идеальным прямоугольным импульсам.

Рисунок 2 – Аппроксимация прямоугольного сигнала путем суммирования различных синусоидальных колебаний

В случае синусоидальных или косинусоидальных сигналов для уравнения 1 можно найти решение в замкнутой форме, и для отображения комплексного спектра будут получены следующие соотношения:

где \(\delta (f-f_0)\) – функция Дирака:

\[\begin \delta (f-f_0) = \begin \infty &\text <если >f-f_0=0 \ \text <, т.е. >f=f_0 \\\ 0 \end \end \\ \int_<-\infty>^ <+\infty>\delta (f-f_0) \ df = 1\]

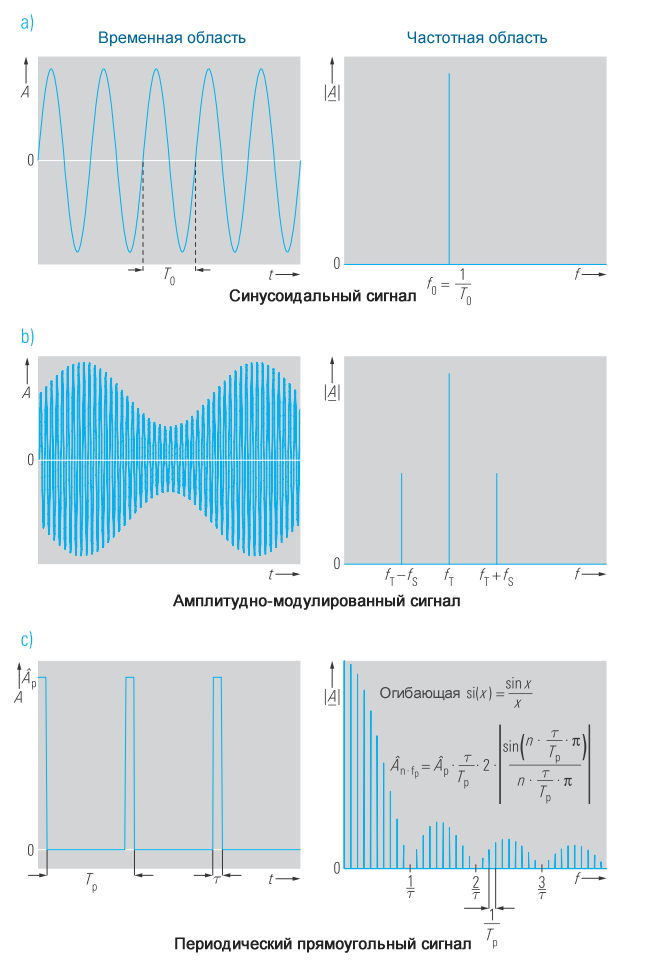
Можно видеть, что частотный спектр и синусоидального, и косинусоидального сигналов является функцией Дирака при f₀ (смотрите рисунок 4a). Преобразования Фурье синусоидального и косинусоидального сигналов идентичны по величине, так что эти два сигнала демонстрируют идентичный амплитудный спектр на одной и той же частоте f₀.

Чтобы вычислить частотный спектр периодического сигнала, временная характеристика которого описывается рядом Фурье в соответствии с уравнением 3, необходимо преобразовать каждый компонент ряда. Каждый из этих элементов приводит к функции Дирака, то есть дискретной составляющей в частотной области. Поэтому периодические сигналы всегда демонстрируют дискретные спектры, которые также называются линейчатыми спектрами. Например, спектр, показанный на рисунке 3, получен для аппроксимированного прямоугольного сигнала на рисунке 2.

Рисунок 3 – Амплитудный спектр аппроксимированного прямоугольного сигнала, показанного на рисунке 2

На рисунке 4 показаны еще несколько примеров периодических сигналов во временной и частотной областях.

Рисунок 4 – Периодические сигналы во временной и частотной области (амплитудные спектры)

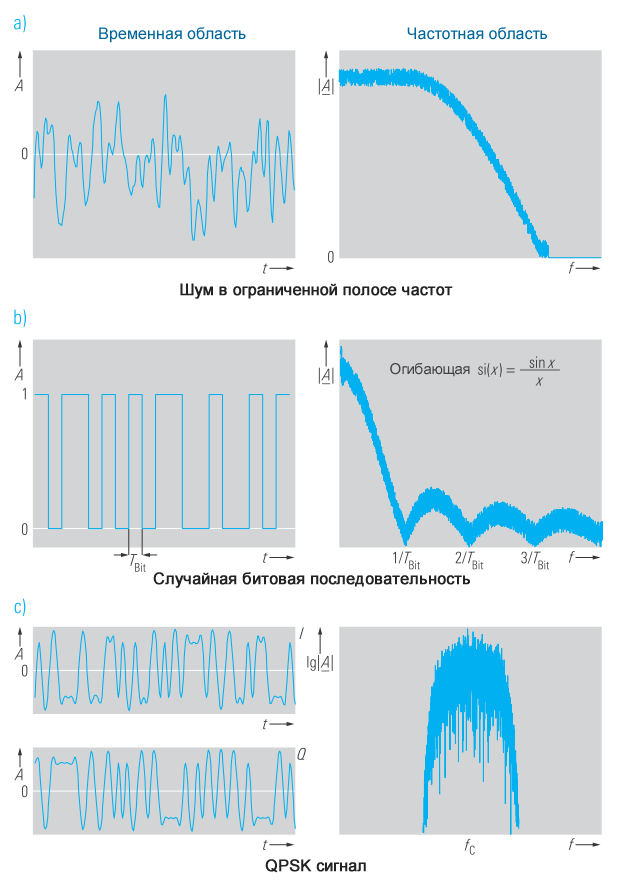
Непериодические сигналы

Сигналы с непериодическим поведением во временной области не могут быть описаны рядом Фурье. Следовательно, частотный спектр таких сигналов не может быть составлен из дискретных спектральных составляющих. Непериодические сигналы демонстрируют непрерывный частотный спектр с частотно-зависимой спектральной плотностью. Представление такого сигнала в частотной области вычисляется с помощью преобразования Фурье (уравнение 1).

Подобно синусоидальным и косинусоидальным сигналам, решение уравнения 1 в замкнутой форме может быть найдено для многих сигналов. Таблицы с такими парами преобразований можно найти в [1].

Для сигналов со случайными характеристиками во временной области, таких как шум или случайные битовые последовательности, решение в замкнутой форме встречается редко. В этом случае частотный спектр легче определить численным решением уравнения 1.

На рисунке 5 показаны некоторые непериодические сигналы во временной и частотной областях.

Рисунок 5 – Непериодические сигналы во временной и частотной областях

В зависимости от типа выполняемого измерения, полезными могут быть исследования либо во временной, либо в частотной области. Например, для измерения джиттера сигнала цифровой передачи данных требуется осциллограф. Для определения содержания гармоник более полезно исследовать сигнал в частотной области.

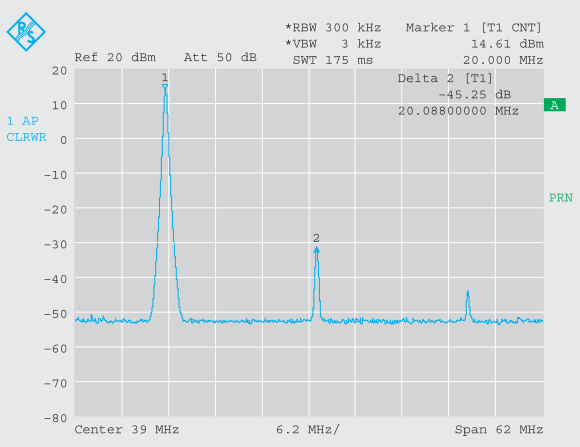
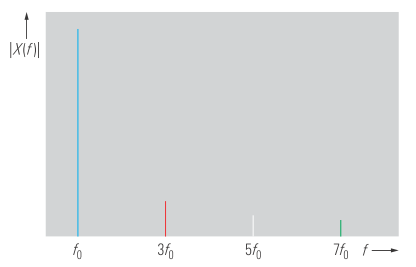
Сигнал, показанный на рисунке 6, кажется чистой синусоидой с частотой 20 МГц. Исходя из приведенных выше соображений, можно было бы ожидать, что его частотный спектр будет состоять только из одного компонента на частоте 20 МГц.

Рисунок 6 – Синусоидальный сигнал (f = 20 МГц), исследуемый на осциллографе

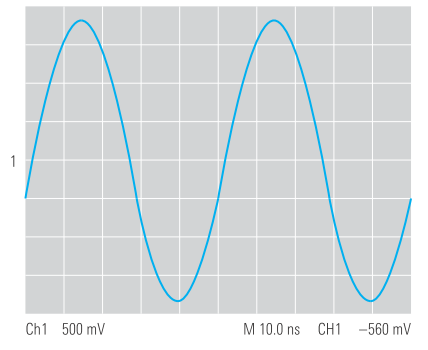
Однако при исследовании сигнала в частотной области с помощью анализатора спектра становится очевидным, что основная гармоника (гармоника 1-го порядка) накладывается на несколько гармоник более высокого порядка, то есть кратные 20 МГц (рисунок 7). Исследуя сигнал во временной области, эту информацию получить нелегко, и практическая количественная оценка высших гармоник невозможна. Кратковременную стабильность частоты и амплитуды синусоидального сигнала намного легче исследовать в частотной области, чем во временной (смотрите также раздел 6.1 «Измерение фазового шума).

Рисунок 7 – Исследование синусоидального сигнала, показанного на рисунке 6, в частотной области с помощью анализатора спектра

Источник